Abstracts
Résumé
Dans le domaine de la psychologie sociale, des recherches font état d’un lien entre la proximité d’un groupe avec un objet de représentation et son degré d’implication. Ayant trouvé des différences dans les représentations sociales des métiers scientifiques de lycéennes et de lycéens de terminale scientifique française (les filles seraient plus proches de l’objet), l’auteure fait l’hypothèse d’une implication différente selon le sexe. Ses résultats montrent que l’implication, mesurée selon trois dimensions, à savoir l’identification personnelle, la valorisation de l’objet et la capacité perçue d’action, se révèle plus forte chez les filles dans le cas de la première dimension. La discussion se fera autour du sens à donner à cette différence : peut-on y voir les premiers résultats d’une pression encourageant les filles à aller vers ces filières ?
Summary
Social psychological studies establish a link between a group proximity to a representational object and its degree of implication about it. Having established that when social representations of scientific professions are proposed to the terminal scientific french students, girls will be closer to this representational object, we put forward the hypothesis that implication is different according to sex. Our results demonstrate that implication, measured in three dimensions, that is to say personal identity, valorisation of the representational object and capacity of possible action, is revealing that the first dimension is predominant among girl students. The discussion will address around the meaning to be given to this difference of implication : can we interpret these first results as stemming from incentives put forth to encourage girls to choose scientific careers ?
Article body
Nous n’en finissons pas d’interroger le rapport des filles à la science, le plus souvent dans un contexte comparatif sexué. L’objet du présent article est de poursuivre cette interrogation en recourant au concept d’implication, que nous définirons et positionnerons en relation avec celui des représentations sociales. La question générale sera alors : des filles qui sont, comme des garçons, engagées dans des filières menant à des métiers scientifiques y mettent-elles la même implication ? Si différences il y a, sur quelles dimensions de l’implication portent-elles et peut-on les expliquer ? Pour terminer, nous verrons en quoi le recours au concept d’implication peut aider à repérer un début de changement dans l’orientation scolaire des filles, alors que les nombreuses actions gouvernementales françaises n’ont pas fait notoirement augmenter le nombre de filles dans les filières scientifiques.
Le concept d’implication et ses différentes déclinaisons
L’implication professionnelle
Ce concept, que nous allons appréhender ici en liaison avec celui de représentations sociales, fait pour le moment l’objet d’une théorisation et de travaux discrets, limités à un cercle restreint de chercheurs et de chercheuses. Il apparaît néanmoins suffisamment puissant pour se poser comme « une variable explicative majeure de la pensée sociale » (Guimelli 1998 : 84). Bataille, pour sa part (2000 : 183-184), s’y intéresse dans le contexte des sciences de l’éducation. Il réfléchit aux liens possibles entre représentations et implication professionnelle, s’appuyant pour cela sur les travaux de Jacquet-Mias (1997) effectués auprès de personnes salariées du secteur médico-social associatif. Cette auteure cherche à comprendre les différences d’investissement des professionnels et des professionnelles, se refusant à considérer la dichotomie « impliqué/non impliqué ». Elle se propose d’articuler le concept d’implication autour de trois dimensions : le sens des actions (S), qui peut être différent pour chacun et chacune, les repères (R), qui dépendent souvent d’une mémoire collective inégalement partagée, et le sentiment de contrôle (C) de son propre parcours professionnel, qui est lié au statut organisationnel. Le tout donne un modèle structural désigné par le triptyque SRC (sens des actions, repères et sentiment de contrôle). Ainsi, les professionnels et les professionnelles vont se positionner plus ou moins complètement sur ces dimensions, et ce, selon la représentation qu’ils ont construite de leur réalité professionnelle. Pour Bataille et autres (1997), l’implication professionnelle serait comme l’« élément énergétique » de ce qu’ils nomment le système des activités professionnelles (SAP). Notons que Pohl (1999) s’est également interrogée sur le concept d’implication en montrant que la distinction entre l’implication à l’égard du travail et l’implication à l’égard de l’activité professionnelle est nécessaire, et en examinant leurs relations. Elle va ainsi trouver une corrélation positive entre les deux, modérée cependant par le statut hiérarchique.
Vers un modèle élargi
Sans se référer exclusivement à l’implication professionnelle, Rouquette (1988, 1997, 1998a, 1998c) cherche à donner une forme opérationnelle au concept d’implication. Son but, en voulant comprendre les diversités d’intérêt des personnes envers les objets sociaux qui sont proposés à leur expérience, est de modéliser les différents niveaux de prise de position. Il conçoit alors ce concept comme un espace à trois dimensions cognitives selon lequel se répartit la pluralité des objets de représentations sociales. Cet espace est composé des dimensions suivantes :
l’identification personnelle (ou encore situation du sujet dans un groupe d’appartenance proche ou non de l’objet de représentation) ;
la valorisation de l’objet, c’est-à-dire l’importance perçue de son enjeu ;
la capacité perçue d’action devant la question posée par l’objet.
Ces trois dimensions sont représentables sur des échelles ordinales de mesure de positionnement individuel ou groupal, permettant de concevoir l’enjeu exprimé par l’objet de représentation. Nous allons successivement les traduire en allant de l’implication minimale à l’implication maximale.
Celle qui est relative à l’identification personnelle va de « cela concerne tout le monde » à « cela concerne moi-même ». La valorisation de l’objet est positionnée de « c’est une question sans importance » à « c’est une question de vie ou de mort », tandis que l’échelle de la capacité perçue d’action varie de « je n’y peux rien » à « tout dépend de moi ». La combinaison des valeurs des extrémités de chacune des trois dimensions fournit huit localisations typiques (Rouquette 1997) du concept d’implication. En notant l’accord 1 et le désaccord 0, il en propose une représentation (1998a : 20) illustrée au tableau 1.
Tableau 1
Combinaison des huit dimensions du concept d’implication
L’implication minimale (m) se définit ainsi : « cette question concerne tout le monde, je la juge sans importance et mon action dessus est nulle ». L’implication maximale (f) sera : « cette question me concerne précisément, je la juge essentielle et mon action peut être déterminante ».
L’implication et les représentations sociales
Ainsi posé, ce concept est désormais fortement lié à celui des représentations sociales. Avant d’en exposer les liens, il nous faut rappeler quelques notions à propos des représentations sociales. On les définit comme un ensemble organisé de croyances et de connaissances (aussi appelées « cognèmes »), élaboré par un groupe à propos d’un objet social qui le concerne. Depuis une quinzaine d’années, on s’intéresse fortement à l’organisation interne – ou structure – de ces représentations (Guimelli 1994). Cela consiste à mettre en évidence les éléments centraux et périphériques. Les éléments centraux (ou « noyau central ») sont les croyances ou connaissances qui font l’objet d’un consensus pour le groupe ; peu nombreuses, elles sont peu sujettes au changement (stables et rigides). Les éléments périphériques témoignent des avis individuels, changent plus facilement et sont moins installés dans le temps. Qu’ils soient centraux ou périphériques, on reconnaît aux éléments d’une représentation diverses dimensions : fonctionnelle, évaluative, descriptive, normative (Rateau 1995). Enfin, grâce à cette organisation en double système de centralité et de périphérie, la comparaison des représentations sociales se fera selon le postulat suivant : des représentations sociales seront différentes si, et seulement si, leur noyau central est différent. Si l’on se focalise sur l’étude de la structure représentationnelle et si l’on attache moins d’importance au contenu, il est reconnu que l’étude comparative des représentations y gagne en acuité.
Pour en revenir aux liens entre implication et représentations sociales, Rouquette (1994 : 63) indique qu’« on fera l’hypothèse générale suivante : lorsqu’il y a implication, et toutes choses égales par ailleurs, la structure des représentations correspondantes comprend, relativement parlant, davantage de cognèmes (structure « enrichie ») et davantage de relations entre ces cognèmes (connectivité élevée de la structure) ». Guimelli (1998), quant à lui, trouve un lien entre le degré d’implication (situation d’acteur versus situation d’observateur) et la structure de rationalisation apparaissant lors de la mise en cause d’une représentation sociale. Reynier (1998), travaillant sur la mise en place et l’évolution de la représentation sociale de la fonction d’infirmière chez des élèves infirmières, mesure le degré d’implication selon ces trois dimensions, chez des élèves de première et de troisième année. Les résultats montrent l’hétérogénéité des trois dimensions par rapport à l’évolution de la représentation. En effet, c’est sur la dimension d’identification personnelle que les élèves, quelle que soit leur classe, donnent le moins de réponses engageantes, quand les deux autres dimensions recueillent des valeurs moyennes. Reynier tente une explication en termes de rapports historiquement sensibles de dépendance entre les infirmières et le corps médical ; il émet ensuite l’hypothèse d’une représentation « idéale » de la fonction. Notons que Garnier et autres (2000 : 126-155), conduisant une importante recherche sur les systèmes de représentations sociales des élèves par rapport à la science et à la technologie, au Québec et au Canada, y incluent plusieurs questionnaires sur l’implication. Cependant, on ne l’aborde pas directement en relation avec les objets « science » et « techniques ». On veut plutôt connaître l’implication des élèves concernant le travail « dans son acception générale ». Cherchant toujours à lier implication et structure représentationnelle, Abric (2000) propose de la considérer comme inhérente à l’un des facteurs agissant dans la désignation des éléments centraux d’une représentation : la distance estimée du groupe étudié par rapport à l’objet. En effet, cette distance dépend du niveau de pratiques que le groupe a sur l’objet, de la connaissance qu’il en a et surtout de l’implication que ressent tel ou tel groupe à l’égard de cet objet.
Quand il ne s’agit pas seulement de « disséquer » une représentation sociale, c’est-à-dire de chercher à connaître son contenu et son organisation, mais de viser la compréhension d’un phénomène social, il apparaît donc pertinent de considérer l’implication comme une variable intermédiaire possible, voire un chaînon entre représentations et actions.
Quelle implication envers les métiers scientifiques selon le sexe en terminale scientifique (TS) ?
L’origine de notre recherche sur l’implication
Dans une recherche précédente (Mariotti 2000), nous avions mis en évidence des différences structurales entre les représentations sociales des métiers scientifiques d’un groupe de 25 lycéens et 24 lycéennes de terminale (dernière année de classe de l’enseignement secondaire du second cycle, avant le diplôme du baccalauréat, où se trouvent des élèves âgés de 16 à 18 ans), en section scientifique (TS). Pour étudier cette représentation, nous avions utilisé la méthode des schèmes cognitifs de base (SCB) de Guimelli et Rouquette (1992). C’est une technique d’association de mots qui permet de considérer les éléments les plus importants de la représentation du point de vue de leur centralité ou de leur périphérie, mais également de repérer leur dimension, fonctionnelle ou évaluative. Il s’agit pour les sujets d’associer par écrit leurs propres mots à l’élément de la représentation qu’on leur soumet ; ce faisant, ils activent entre les deux des connexions (ou connecteurs) qui peuvent être fonctionnelles, rattachées à l’action, ou bien évaluatives, c’est-à-dire plutôt pensées comme un jugement. Pratiquement, cela se passe ainsi :
après que les sujets ont effectué la tâche d’association de mots, une liste de dix-neuf connecteurs déjà formalisés leur est présentée : douze sont d’ordre fonctionnel (ils sont appelés, dans la méthode, SCB « Praxie ») et sept sont d’ordre évaluatif (et sont appelés SCB « Attribution ») ;
en repensant aux mots qu’ils ont eux-mêmes associés, les sujets indiquent pour chacun des dix-neuf connecteurs de la liste si c’est bien lui qu’ils ont employé.
Il faut savoir que la méthode des SCB prévoit de faire associer des mots ou à l’objet de représentation lui-même (ici, « métiers scientifiques »), ou bien à des éléments de la représentation repérés comme importants dans le discours que les sujets tiennent à propos de cet objet. Nous avons opté pour la seconde solution, et, pour cela, nous avons réalisé des entretiens exploratoires sur le thème des métiers scientifiques. Deux éléments sont apparus récurrents dans le discours des filles et des garçons de TS : l’importance quasi hégémonique des mathématiques et le choix des débouchés offerts. Ce sont donc ces deux éléments, « mathématiques » et « débouchés », que nous avons présentés aux sujets pour associations de mots (ou l’un ou l’autre, un groupe différent pour chaque mot). Divers calculs nous permettaient ensuite de considérer pour chaque groupe la centralité ou la périphérie de chaque élément, puis de voir si les connecteurs avaient plutôt été reconnus dans leur dimension fonctionnelle (choix prioritaire des connecteurs du SCB « Praxie » dans la liste) ou dans leur dimension évaluative, par le choix des connecteurs du SCB « Attribution » (pour les détails complets de la méthode et les calculs, voir à ce sujet Rouquette et Rateau (1998). Les résultats sont résumés dans le tableau 2. Pour chaque groupe, il est indiqué si les éléments « mathématiques » et « débouchés » sont centraux ou périphériques et s’ils ont une dimension du type fonctionnel (praxie), du type évaluatif (attribution), ou bien, le cas pouvant se présenter, les deux à la fois.
Tableau 2
Statut et dimension des deux éléments de la représentation des métiers scientifiques chez les filles et les garçons de TS
Nous constatons que la différence porte principalement sur l’élément « mathématiques ». Il est central pour les filles et périphérique pour les garçons. De plus, il présente pour les garçons un caractère fortement évaluatif, tandis que, pour les filles, les dimensions fonctionnelles et évaluatives sont équilibrées. Or, dans un récent bilan sur la notion de noyau central, Abric (2000) faisait remarquer que, selon la finalité de la situation perçue par les sujets, un élément central pouvait être plutôt fonctionnel ou plutôt évaluatif, le côté fonctionnel primant lorsque le groupe a une distance réduite par rapport à l’objet.
Ainsi, d’après nos résultats, les filles de TS seraient, contre toute attente, plus proches de l’objet de représentation « métiers scientifiques » que les garçons de TS, alors que ce sont eux les héritiers de cette tradition scientifique. Notons que cette proximité avec l’objet n’est pas totale, puisqu’elle est pour l’instant sans pratiques, comme en témoigne pour les filles l’indécision qui apparaît dans le fait de considérer également les mathématiques du point de vue à la fois fonctionnel et évaluatif.
Alors, si les différences sexuées que nous avons observées pour l’élément mathématiques, et sur le statut (central versus périphérique) et sur la dimension (fonctionnelle/évaluative versus évaluative), ne sont pas dues à un artefact ni à une variable intermédiaire, mais imputables à des ancrages positionnels issus d’une histoire spécifique, nous pouvons faire l’hypothèse générale que nous allons retrouver ces différences au sujet de la mesure de l’implication entre les filles et les garçons de TS. Nous pouvons donc nous attendre que les filles, plus proches de l’objet selon notre première recherche, se montrent plus impliquées que les garçons.
La méthode et la procédure retenues
Les trois dimensions proposées par Rouquette nous ont semblé appropriées pour une mesure de l’implication chez des sujets de terminale. Nous avons donc élaboré un questionnaire relatif à ces dimensions à partir d’un corpus de réponses (Mariotti 2000) à la question suivante : « Qu’est-ce que pour vous un métier scientifique ? », posée à 44 collégiens et 44 collégiennes de troisième (dernière année de classe de l’enseignement secondaire du premier cycle). La rédaction de quelques propositions a été affinée grâce à des témoignages de sujets déjà engagés dans des filières scientifiques, figurant dans le rapport du séminaire européen portant sur l’évaluation des plans académiques en faveur de la diversification de l’orientation des filles (1995). Nous avons établi trois types de propositions par dimension :
-
les propositions relatives à l’identification personnelle (IP) :
« Ce sont des métiers particuliers qui demandent un investissement très important de soi-même » ;
« J’ai l’impression que c’est un type de métier qui correspond bien à ma personnalité » ;
« J’ai choisi ce type de métier parce que je me suis identifié-e à une personne qui l’exerce déjà » ;
-
les propositions relatives à la valorisation de l’objet (VO) :
« Pour me préparer à mon futur métier, je m’informe le plus possible sur ses divers aspects » ;
« J’essaie déjà d’intégrer dans mes loisirs quelques aspects de mon futur métier » ;
« Les préoccupations qui sont derrière ce type de métiers sont les miennes dans ma vie » ;
-
les propositions relatives à la capacité perçue d’action (CPA) :
« Mon parcours professionnel tout au long de ma vie se fera autant que possible dans le secteur scientifique » ;
« Je me sens capable d’apporter des innovations dans le domaine de mon futur métier » ;
« J’ai l’intention de monter les échelons pour progresser dans mon métier ».
Une proposition a été ajoutée pour voir si la question de la masculinité/féminité associée à ce type de métier était ressentie par les sujets :
« Ce genre de métier est particulièrement adapté au fait que je sois une fille (ou un garçon) ».
En effet, Marro (1992) pose le même type de question à des élèves de seconde, au début des années 90 : « Pensez-vous que ces professions conviennent plutôt aux garçons, aux filles, ou indifféremment aux deux sexes ? » Au total, 66 % des sujets répondent « indifféremment aux deux sexes », mais parmi les jeunes qui ont un projet scientifique, on trouve 72 % de filles et 64 % de garçons. Ayant comme sujets des terminales scientifiques (deux ans de plus que les secondes), nous avons voulu vérifier si ce léger décalage sexué perdurait.
La variable indépendante et les sujets
La variable indépendante (VI) est ici le sexe des sujets (F, G).
Nous avons interrogé 26 filles et 27 garçons de terminale scientifique d’un lycée de Montpellier (sud de la France) de catégories socioprofessionnelles (CSP) moyennes à hautes (ces sujets ne sont pas ceux qui ont été interrogés sur la représentation sociale des métiers scientifiques).
La tâche confiée aux élèves
La passation du questionnaire s’est déroulée en fin d’année scolaire 1997-1998, sous l’égide des professeures et professeurs principaux qui l’ont distribué aux élèves volontaires afin qu’ils et elles y répondent à leur domicile. Les sujets avaient d’abord à lire un petit texte de présentation : « Vous êtes en terminale S, filière qui ouvre la porte à de nombreux métiers scientifiques. Il vous est demandé de donner votre avis personnel sur les thèmes suivants qui concernent ces métiers scientifiques. Pour chacun, vous entourerez le chiffre correspondant à votre degré d’accord selon l’échelle ci-dessous [...] ».
Une échelle du type Likert en six points était présentée à la suite de chacune des dix propositions, allant de 1 (pas du tout d’accord) à 6 (tout à fait d’accord). La présentation des propositions a été randomisée.
Comme pour tous les questionnaires que nous avons fait passer, un dernier feuillet concerne l’identité des sujets. Elle est présentée comme facultative, mais la quasi-totalité des sujets a marqué son nom. Nous précisons ce fait, car certains auteurs et auteures ont remarqué un effet de l’individuation versus l’anonymat sur les réponses (Gosling et Wach 1996), l’individuation étant bien sûr plus engageante.
La variable dépendante et l’hypothèse expérimentale
La variable dépendante (VD) est le score moyen recueilli pour chaque dimension selon le sexe. Le score de la question sur le genre n’a pas été comptabilisé dans les résultats.
Notre hypothèse expérimentale est la suivante : Il existe une liaison entre le sexe et les scores obtenus.
Quel sexe se montre le plus impliqué ?
En premier lieu, nous allons attacher de l’importance au nombre de sujets impliqués selon le sexe, d’abord en fonction de l’ensemble des propositions (implication globale), puis par dimension. Sont considérés comme impliqués les sujets dont le score moyen sur les neuf propositions est supérieur à 3,5. Pour le score par dimension, un sujet est considéré comme impliqué par rapport à la dimension x quand son score moyen des trois propositions relatives à cette dimension est supérieur à 3,5. Nous avons traité ces résultats en étudiant la liaison possible entre le sexe et le nombre de sujets impliqués avec le test du chi-deux ((2) corrigé de Yates.
En second lieu, nous présenterons les résultats concernant le degré d’implication pour chaque dimension, les moyennes étant comparées avec une analyse de variance d’ordre un ; puis un graphique récapitulera les moyennes des deux groupes dans le cas des trois dimensions. La discussion se fera à l’issue de ces deux parties.
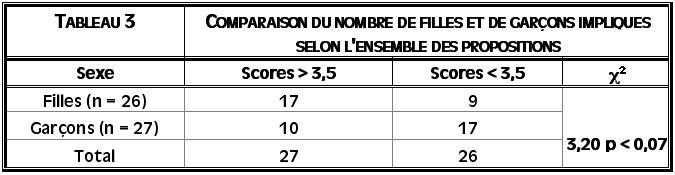
Le tableau 3 indique le nombre de sujets impliqués d’une façon globale, c’est-à-dire en tenant compte des neuf propositions :
Tableau 3
Comparaison du nombre de filles et de garçons impliqués selon l’ensemble des propositions
On constate ici un lien entre la variable « sexe » et le fait d’être impliqué. Le nombre de filles impliquées est supérieur au nombre de garçons impliqués et elles sont plus nombreuses à être impliquées (17) que non impliquées (9), alors que c’est l’inverse pour les garçons (10 impliqués en regard de 17 non impliqués). Les tableaux 4, 5 et 6 vont nous aider à mettre en évidence la ou les dimensions où peuvent se situer des différences.
Les résultats concernant la dimension de l’identification personnelle
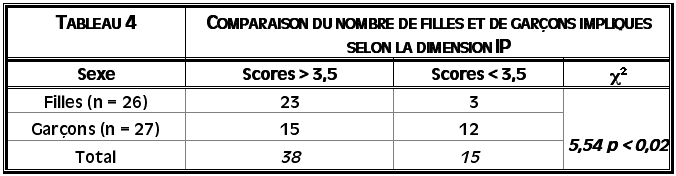
Le tableau 4 illustre les résultats obtenus concernant la dimension de l’identification personnelle (IP).
Tableau 4
Comparaison du nombre de filles et de garçons impliqués selon la dimension IP
Lors de l’analyse de dimension IP, on observe également un lien entre le sexe et le nombre de sujets impliqués : il y a ici nettement plus de filles impliquées que de garçons. D’autre part, notons que le nombre de sujets impliqués est plus important que le nombre de sujets non impliqués, quel que soit le sexe.
Les résultats concernant la dimension de la valorisation de l’objet
Le tableau 5 regroupe les résultats obtenus au sujet de la dimension de la valorisation de l’objet (VO).
Tableau 5
Comparaison du nombre de filles et de garçons impliqués selon la dimension VO
On ne remarque aucun lien entre le sexe et le nombre de sujets impliqués pour la dimension VO. Comme pour la dimension IP, le nombre de sujets impliqués est ici supérieur au nombre de sujets non impliqués.
Les résultats concernant la dimension de la capacité perçue d’action
Au tableau 6 sont réunis les résultats à propos de la dimension de la capacité perçue d’action (CPA).
Tableau 6
Comparaison du nombre de filles et de garçons impliqués selon la dimension CPA
Encore une fois, il n’y a pas de lien entre le sexe et le nombre de sujets impliqués pour cette dimension. Il y a également plus de sujets impliqués que de non impliqués.
Avant de passer à l’examen des résultats concernant le degré d’implication, donnons les scores moyens sur la proposition relative à l’adéquation avec son sexe (« Ce genre de métier est particulièrement adapté au fait que je sois une fille (ou un garçon) ») :
filles : 2,31 ;
garçons : 1,92.
Les moyennes ne sont pas différentes : F (1,51) = 0,84 NS. Si l’on rappelle que les chiffres 1 et 2 de l’échelle indiquent « pas du tout d’accord » et « pas d’accord », on constate, quel que soit le sexe, le rejet massif de la question du genre associée au fait de faire un métier scientifique. Mentionnons cependant les 6 filles et les 3 garçons qui ont des moyennes comprises entre 4 et 6, et qui sont donc d’accord avec la proposition. Ces filles-là se voient, pour la plupart, exercer des métiers de la santé (vétérinaire, biologiste, sage-femme), tandis que ces garçons veulent être pilote de chasse, ingénieur et scientifique. On pourrait considérer ces sujets comme plus « stéréotypants » que le reste du groupe.
Les résultats concernant le degré d’implication
Dans le tableau 7 figurent les moyennes obtenues pour chaque sexe selon la dimension. Pour chaque dimension, on trouve les moyennes des sujets considérés comme impliqués, puis de l’ensemble des sujets. En effet, il nous a semblé utile de faire également une analyse de variance sur les moyennes des sujets impliqués, car trouver plus de filles impliquées que de garçons n’entraîne pas nécessairement chez elles un degré d’implication plus élevé ; peut-être même pourrait-on envisager le contraire.
Tableau 7
Analyse de variance des moyennes selon les dimensions (ip, vo, cpa)*, les sujets impliqués et tous les sujets
Les moyennes des garçons impliqués sont supérieures à celles des filles impliquées pour les dimensions VO et CPA, mais ces différences ne sont pas significatives. En fait, on ne constate pas de différence de degré d’implication entre les filles et les garçons, sauf pour la dimension IP envisagée avec l’ensemble des sujets (F(1,51) = 8,06 p < 0,006). Dans la mesure où nous avions trouvé un nombre plus important de filles impliquées que de garçons pour cette dimension ((2 = 5,54 p < 0,02), ce résultat ne nous étonne pas puisqu’il prend en considération la faiblesse relative de la moyenne des garçons. Il ne fait que confirmer la différence entre les sexes concernant la dimension IP.
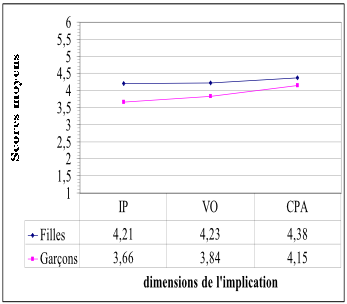
Il nous faut maintenant considérer l’importance du degré d’implication donnée par les moyennes. Comment ces sujets sont-ils impliqués ? Nous avons trouvé dans l’ensemble plus de sujets impliqués que non impliqués, et les moyennes consignées dans le tableau 6 sont toutes supérieures à 3,5, chiffre que nous avons fixé comme représentant le minimum d’implication. Une représentation graphique de l’ensemble des moyennes par dimension va nous permettre d’avoir une vision globale des degrés d’implication selon le sexe (voir le graphique 1).
Graphique 1
Scores moyens selon le sexe pour chacune des trois dimensions de l’implication
L’échelle de Likert partageait les degrés d’accord en deux pôles : un pôle négatif de 1 à 3, et un pôle positif de 4 à 6. Dans l’ensemble, et bien que la présentation selon les moyennes ait tendance à « aplatir » les résultats, les courbes montrent que les sujets se sont situés dans le pôle de l’accord, au-dessus de 3,5. Les filles sont toujours légèrement au-dessus des garçons. Les moyennes varient de 3,66 (IP chez les garçons) à 4,38 (CPA chez les filles). Il y a donc bien implication, mais elle n’est pas maximale, ce qui peut sembler compréhensible étant donné la relative distance à l’objet que peut représenter un métier pour des élèves de terminale générale qui se dirigent plutôt vers des études longues. Nous allons synthétiser ces résultats dans la discussion suivante.
Les interprétations psychosociologiques et les traductions sexuées des dimensions de l’implication
Nous avons trouvé plus de filles que de garçons impliqués globalement selon le codage que nous avons établi, à savoir un score moyen supérieur à 3,5. À partir du détail selon les dimensions, on peut remarquer qu’il y a pour chacune plus de sujets impliqués que de sujets non impliqués et que la différence selon le sexe la plus significative porte sur l’identification personnelle, plus élevée chez les filles. Les données vont dans le sens de notre hypothèse.
À partir de ces résultats, nous pouvons tenter un rapprochement avec la différence de structure repérée dans l’étude sur la représentation des métiers scientifiques chez les TS et la mesure de l’implication. Nous avons trouvé un élément central, les mathématiques, chez les filles, mais pas chez les garçons, puis plus de filles impliquées que de garçons. Ces deux résultats vont dans le même sens, mais nous ne pouvons pas établir entre eux un lien de cause à effet, car, pour l’envisager, nous aurions dû auparavant examiner le statut des éléments selon le facteur du degré d’implication. Ils nous engagent néanmoins à penser que les liens entre le concept d’implication et la structure des représentations sociales méritent d’être approfondis. D’autant plus que ce n’est pas sur la même population de sujets que nous avons travaillé pour ces deux recherches. Cependant, selon les hypothèses en vigueur actuellement sur les liens entre structure et implication, il est envisageable de penser que notre questionnaire mesurant l’implication aurait donné les mêmes résultats chez les sujets TS que nous avions interrogés sur la représentation des métiers scientifiques. Peut-on cependant généraliser ces résultats dans la mesure où nous ne pouvons affirmer que nos populations d’étude sont homogènes du point de vue de leur désir de se lancer vers des carrières scientifiques, ce qui pourrait entraîner des différences d’implication ? Nous ne nous y risquerons pas pour l’instant, mais la piste semble prometteuse.
Dès lors, comment faut-il interpréter ces résultats du point de vue psychosociologique ? Sachant que de très nombreuses actions ont eu pour objet d’inciter les filles à aller vers les filières scientifiques et techniques, mais sans pour autant donner de résultats chiffrés marquant une réelle progression, on pourrait s’étonner de trouver autant de filles impliquées. À moins que ce ne soit là justement un des premiers effets de cette pression sociale que les filles commenceraient à percevoir ? D’autre part, en ce qui concerne les garçons, nous savons combien la filière scientifique S est considérée comme automatique pour ceux d’un bon niveau scolaire et issus de CSP moyennes à élevées ; peut-être ne faut-il alors pas s’étonner de constater qu’il y en ait moins d’impliqués dans notre échantillon ?
C’est là que l’analyse selon la dimension du concept d’implication peut apporter un début d’explication. Il est intéressant d’observer la différence fortement significative au sujet de l’IP. Aurait-elle un lien avec le type de métiers vers lequel les élèves se dirigent ? Dans notre échantillon, la moitié des filles (13) envisagent des métiers en rapport avec le vivant, 4 se tournent vers l’enseignement, donc se conformeraient plutôt aux rôles sociaux attendus pour le genre féminin. Les garçons, quant à eux, sont plus indéterminés sur leur désir : 5 n’indiquent pas de choix de métiers, 2 ne précisent pas dans quel domaine ils veulent être ingénieurs, et pour les autres, les indications de métiers sont peu précises : « activités comprenant voyage, temps de liberté, contacts, ou activité scientifique, ou encore recherche scientifique ». Chez les garçons, 5 veulent travailler dans l’informatique. Leurs métiers reflètent également la conformité aux rôles sociaux masculins. Un seul veut être ingénieur biochimiste. Cependant, rien de clairement opposable ne ressort de l’examen des métiers envisagés, dans le sens où, pour nous, chacun des sexes reste peu ou prou dans son domaine d’attribution stéréotypé ; en conséquence, l’IP devrait alors être comparable.
L’on peut également envisager un lien avec la pression sociale, différente pour chaque sexe, et peut-être ressentie diversement par les uns et les autres : pour les filles, c’est l’incitation médiatisée, valorisée, alors ressentie positivement, qui entraînerait un réel choix d’aller en S ; pour les garçons, c’est la pression résultant d’une norme, qui commencerait à lasser, entraînant une relative indifférence pour l’attrait de la terminale S. Cette dernière piste nous paraît pour l’instant plausible, car elle s’inscrit dans un réel contexte idéologique de désertion des sciences, mais nos résultats mériteraient d’être repris à plus grande échelle. Ajoutons que, par rapport à l’illégitimité historique des filles à se trouver dans ce type de filière, cette implication plus forte concernant l’IP pourrait en être la résultante, un contre-balancement en quelque sorte, vu comme une revanche à prendre.
Pour les dimensions CPA et VO, on ne constate aucune différence de sexe dans le nombre de sujets impliqués ni dans leur degré d’implication. Ces deux dimensions seraient-elles moins marquées par le fait d’être un garçon ou une fille dans une filière conforme ou non à son sexe ? Nous aurions alors mesuré une projection dans le futur, quel que soit le type de métier envisagé.
D’autre part, que peut nous dire le degré d’implication de nos sujets par rapport à la distance à l’objet de représentation « métiers scientifiques » ? Nous avons considéré dans les paragraphes précédents que nos sujets étaient impliqués, mais il faut moduler cette implication. Certes, ils sont au-dessus du score moyen de 3,5 que nous avons décidé de considérer comme le seuil minimum d’implication. Cependant, ce degré n’est pas très élevé. En fait, nous manquons d’éléments de comparaison pour statuer correctement sur ce degré. Il nous faudrait pour cela mesurer l’implication chez des élèves plus avancés (donc plus proches de l’objet de représentation) : peut-être y trouverions-nous des moyennes supérieures à 4,5 ?
Enfin, revenons aux déclinaisons proposées par Rouquette pour chaque dimension du concept d’implication. Dans sa représentation en tableau (voir le tableau 1), il réduit les pôles en négatif (0) et positif (1), mais il en décrit les variations : pour la dimension IP, entre « cela concerne l’espèce (0) » et « cela me concerne moi (1) », il signale la possible existence de groupes de moins en moins étendus, d’un grand nombre ou de quelques-uns. Pour la dimension VO, entre « je ne lèverais pas le petit doigt pour cela (0) » et « je tuerais (1) », il évoque d’autres attitudes comme parler, manifester, voire « pétitionner ». Et pour la dimension CPA, cela varie de « la vanité de tout effort (0) », en passant par l’association à une action, jusqu’à la conviction d’ « une action significative (1) ». Selon ce modèle, nous proposons, à partir de nos résultats, un résumé des degrés d’implication des groupes que nous avons étudiés, en partant des propositions que nous leur avons soumises.
Cela se traduirait ainsi pour les filles :
IP : « Au sujet des métiers scientifiques, je suis consciente que ce type de métiers demande de l’investissement et il correspond assez à l’idée que je me fais de moi » ;
VO : « Je suis relativement proche des préoccupations existant derrière ce type de métiers et je m’intéresse à ses divers aspects que j’essaie d’intégrer à mes loisirs » ;
CPA : « J’ai l’intention de progresser dans mon futur métier en restant si possible dans le secteur scientifique, et peut-être y apporterai-je des innovations ».
Pour les garçons, n’ayant trouvé de différence très significative que pour la dimension IP, nous n’indiquons une variante que pour cette dimension, le résumé pour la VO et la CPA des filles restant valables pour eux :
IP : « Au sujet des métiers scientifiques, je suis assez conscient que ce type de métiers demande un certain investissement et il correspond plus ou moins à l’idée que je me fais de moi ».
Quant à notre proposition solitaire sur l’accord du genre et des métiers scientifiques, l’avis général se traduit ainsi :
« Les métiers scientifiques correspondent aussi bien aux filles qu’aux garçons ».
À ce sujet, Terlon (1989) avait obtenu le même type de résultats au cours d’une enquête sur l’attitude des adolescents et des adolescentes à l’égard de la technologie. Cependant, Marro (1992) postulait que cette convenance quant au sexe manquait encore d’affirmation, surtout chez les garçons. Elle trouvait des nuances selon le type de métiers. Par exemple, les avis étaient partagés sur le métier d’ingénieur, 50 % des élèves pensant que ce métier convient aux deux sexes, et 50 % qu’il convient plus aux garçons. Et que penser de la réponse sur la convenance réservée précisément au genre féminin ? En moyenne, 5 % de sujets à projet scientifique préféraient cette réponse, mais chez les sujets à projet non scientifique les garçons étaient plus affirmatifs (11 %) que les filles (6 %). Nos sujets, interrogés en 1998, sont moins nuancés, mais peut-être faut-il y voir l’effet d’une norme égalitaire qu’il est de bon ton de respecter.
Conclusion
Les recherches exploratoires que nous venons de présenter ne sont pas encore généralisables à l’ensemble de la population visée. En effet, si les travaux sur les structures des représentations sociales se font traditionnellement avec un échantillon restreint de sujets (des recherches menées sur un plus grand nombre de sujets donnent les mêmes résultats), le questionnaire sur l’implication que nous avons produit mériterait d’être appliqué à une plus vaste population, car les objectifs théoriques sont différents. Lorsqu’on recherche ce qui est central dans la représentation d’un objet, on s’intéresse aux opinions, aux croyances, aux connaissances qui rassemblent un groupe sur cet objet particulier. Ainsi, la centralité se repère facilement dans de petits groupes. En ce qui concerne les travaux sur l’implication, qui sont nouveaux, l’utilisation de petits groupes de sujets n’est pas encore justifiée théoriquement.
Nous pouvons avancer néanmoins, compte tenu de ce préalable, que notre recherche sur l’implication, menée à la suite de travaux sur la structure d’une représentation sociale, nous semble renforcer le lien théorique qu’il est désormais possible d’établir entre les deux concepts. En effet, une implication plus élevée chez des filles de TS peut être mise en parallèle avec la proximité de l’objet « métiers scientifiques » concernant des filles TS d’un autre lycée, proximité qui découlerait du caractère mixte fonctionnel/évaluatif de l’élément central de la représentation, les mathématiques. Comme l’ont pressenti Garnier et autres (2000), l’implication doit désormais faire partie des études sur les représentations, surtout lorsqu’elles sont étudiées en système et, a fortiori, lorsqu’on s’interroge sur la genèse des représentations des métiers. On remarquera, d’autre part, combien la distinction en trois dimensions proposée par Rouquette peut se montrer opérationnelle pour comprendre une situation sociale.
Cependant, dans l’état actuel des travaux récents sur l’implication, rien ne nous permet d’affirmer que l’implication des filles – si peu nombreuses soient-elles – qui s’investissaient dans des filières et des métiers scientifiques avant les actions d’incitations gouvernementales n’ait pas été comparable à celle obtenue dans nos résultats actuels. Nous ne savons pas non plus si cette différence sexuée est nouvelle ou a toujours été présente, les filles étant reconnues comme des actrices plus performantes que les garçons dans l’ensemble de leur parcours scolaire (Vouillot 1999). Cependant, il n’est quand même pas anodin de constater que la différence porte ici sur la dimension de l’identification personnelle. Ces filles-là ont répondu comme si elles se réappropriaient un savoir. Si cette interprétation s’avère confirmée par de nouvelles recherches sur l’implication, c’est qu’il se peut bien que les programmes de promotion des sciences pour les filles aient un effet mesurable. On imagine alors l’enjeu que cela peut représenter en matière d’études féministes, d’autant plus que, comme le rappelle Sirinelli, président de la Commission française pour l’UNESCO (1995), l’insertion des filles vers les études et recherches scientifiques ainsi que leur formation même sont posées comme un problème mondial, et ce, depuis la Quatrième Conférence des Nations Unies sur les femmes à Beijing. Ainsi, les nouvelles méthodes et théories disponibles en sciences sociales, pour peu qu’elles arrivent à entrer dans le champ de l’interdisciplinarité en la matière, devraient contribuer à mesurer les avancées et reculs de l’accès des femmes à la science.
Appendices
Note biographique
Françoise Mariotti
Françoise Mariotti est docteure en psychologie sociale, attachée au Laboratoire de psychologie sociale de l’Université de Paris 8. Elle est actuellement enseignante vacataire en psychologie sociale. Ses recherches portent sur la genèse du champ représentationnel de la science selon le sexe auprès d’élèves de 10 à 18 ans. Elle a publié notamment « Place et statut des mathématiques selon le sexe dans la structure des représentations sociales de la science et des métiers scientifiques chez des collégiens et des lycéens » (Les Cahiers internationaux de psychologie sociale, 49, 2001 : 78-96). Elle est également présidente de l’Association féministe Citoyennes maintenant, à Montpellier.
Références
- ABRIC, Jean-Claude, 2000 « La notion de noyau central : bilans et perspectives actuelles », dans Actes de la Cinquième Conférence internationale sur les représentations sociales, tenue à Montréal, du 29 août au 2 septembre : 87-88.
- BATAILLE, Michel, 2000 « Représentation, implicitation, implication », dans Catherine Garnier et Michel-Louis Rouquette (dir.), Représentations sociales et éducation. Montréal, Éditions nouvelles : 165-188.
- BATAILLE, Michel, et autres, 1997 « Représentations sociales, représentations professionnelles, système des activités professionnelles », L’Année de la recherche en sciences de l’éducation : 57-89.
- Évaluation des plans acadÉmiques en faveur de la diversification de l’orientation des filles, 1995 Séminaire européen, Paris, 6 et 7 novembre.
- GARNIER, Catherine, et autres, 2000 Systèmes de représentations sociales d’élèves du secondaire, de leurs parents et de leurs enseignants en science et technologie, Rapport synthèse de recherche. Montréal, Centre interdisciplinaire de recherche sur l’apprentissage et le développement en éducation (CIRADE), Université du Québec à Montréal.
- GOSLING, Patrick, et M. WACH, 1996 « L’évaluation des métiers au moyen de dimensions : effet du choix par l’élève de ses propres métiers et dimensions, du statut scolaire et de l’implication de l’élève », L’Orientation scolaire et professionnelle, 25, 1 : 77-95.
- Guimelli, Christian, 1998 « Implication, perception de la situation et représentations sociales : étude expérimentale », dans Actes du Deuxième Congrès international de psychologie sociale en langue française, tenu à Turin, du 17 au 19 septembre : 84-85.
- Guimelli, Christian (dir.), 1994 Structures et transformations des représentations sociales. Neuchâtel, Delachaux et Niestlé : 171-198.
- GUIMELLI, Christian, et Michel-Louis ROUQUETTE, 1992 « Contribution du modèle associatif des schèmes cognitifs de base à l’analyse structurale des représentations sociales», Bulletin de psychologie, XLV, 405 : 196-202.
- JACQUET-MIAS, C., 1997 L’implication professionnelle des travailleurs sociaux du secteur médico-social associatif. Thèse de doctorat en sciences de l’éducation. Toulouse, Université de Toulouse-Le Mirail.
- MARIOTTI, Françoise, 2000 Études expérimentales des représentations sociales de la science et des métiers scientifiques selon le sexe au collège et au lycée. Thèse de doctorat. Paris, Université Paris VIII.
- MARRO, Cendrine, 1992 Garçons et filles face à la science. Similarités et divergences quant aux variables intervenant dans le choix d’une orientation scientifique chez les deux sexes. Thèse de doctorat nouveau régime. Paris, Université Paris V.
- POHL, Sabine, 1998 « Contribution à une analyse des relations entre l’implication à l’égard du travail et l’implication à l’égard de l’activité professionnelle », L’Orientation scolaire et professionnelle, 28, 3 : 393-404.
- RATEAU, Patrick, 1995 « Dimensions descriptive, fonctionnelle et évaluative des représentations sociales – une étude exploratoire », Papers on Social Representations, 4, 2 : 133-146.
- Reynier, Jérôme, 1998 La représentation sociale de la fonction d’infirmière : une étude de sa mise en place et de son évolution. Thèse de doctorat nouveau régime. Montpellier, Université Paul Valéry.
- ROUQUETTE, Michel-Louis, 1994 Sur la connaissance des masses. Essai de psychologie politique. Grenoble, Presses universitaires de Grenoble.
- ROUQUETTE, Michel-Louis, 1997 La chasse à l’immigré. Violence, mémoire et représentations. Liège, Mardaga.
- ROUQUETTE, Michel-Louis, 1998a La communication sociale. Paris, Dunod.
- ROUQUETTE, Michel-Louis, 1998b La psychologie politique. Paris, PUF.
- ROUQUETTE, Michel-Louis, 1998c « Sur la construction des mondes politiques », Bulletin de psychologie, 51, 1, 433 : 41-43.
- ROUQUETTE, Michel-Louis, et Patrick RATEAU, 1998 Introduction à l’étude des représentations sociales. Grenoble, Presses universitaires de Grenoble.
- SIRINELLI, Jean, 1995 « Avant-propos », dans La formation scientifique des filles, un enseignement au-dessus de tout soupçon ? UNESCO, Éditions Liris.
- TERLON, Claire, 1989 « Attitudes des adolescent(e)s à l’égard de la technologie : une enquête internationale », Revue française de pédagogie, 90, janvier-février-mars : 51-60.
- VOUILLOT, Françoise (dir.), 1999 Filles et garçons à l’école : une égalité à construire. Paris, Centre national de documentation pédagogique.
List of figures
Graphique 1
Scores moyens selon le sexe pour chacune des trois dimensions de l’implication
List of tables
Tableau 1
Combinaison des huit dimensions du concept d’implication
Tableau 2
Statut et dimension des deux éléments de la représentation des métiers scientifiques chez les filles et les garçons de TS
Tableau 3
Comparaison du nombre de filles et de garçons impliqués selon l’ensemble des propositions
Tableau 4
Comparaison du nombre de filles et de garçons impliqués selon la dimension IP
Tableau 5
Comparaison du nombre de filles et de garçons impliqués selon la dimension VO
Tableau 6
Comparaison du nombre de filles et de garçons impliqués selon la dimension CPA
Tableau 7
Analyse de variance des moyennes selon les dimensions (ip, vo, cpa)*, les sujets impliqués et tous les sujets