Abstracts
Résumé
L’histoire des signes employés par les (al) chimistes révèle qu’il a surtout été fait appel à deux modes d’association d’un signifiant à son signifié : l’iconisme et la convention. Leur évolution peut se diviser en trois périodes : l’alchimie, la révolution berzélienne et la chimie contemporaine. Les alchimistes ont créé des signes graphiques basés sur des analogies symboliques (pour les substances chimiques, non représentables iconiquement à l’échelle macroscopique), ou sur un iconisme pur et simple (pour les appareils et les opérations). Ils n’ont toutefois jamais élaboré un système entièrement cohérent. Lavoisier et Berzelius ont tourné le dos à ce type de signes pour adopter des signes alphabétiques conventionnels. Cependant le développement moderne de la chimie a rendu nécessaire un retour à l’iconisme (représentation spatiale des molécules). Ceci a été obtenu en ajoutant au système de Berzelius des éléments graphiques en relation d’iconisme avec le modèle supputé des molécules (qui demeurent invisibles). Il en est résulté un système hybride tout à fait original et opérationnel.
Abstract
The history of the signs used by (al)chemists reveals that two main modes were employed to associate a signifier to its signified: iconism and convention. Their evolution can be divided in three periods: alchemy, the berzelian revolution, and contemporary chemistry. The alchemists created graphic signs based on symbolic analogies (because chemical substances are impossible to represent iconically at the macroscopic level), or on a straightforward iconism (for equipment and operations). Nevertheless they never achieved a completely coherent system. Lavoisier and Berzelius rejected this type of signs, prefering the use of conventional alphabetic signs. However, the development of modern chemistry prompted a return to iconism, for the spatial representation of molecules. This was obtained by adding to the berzelian system graphic elements that were iconically related to the assumed model of the molecules (which remain invisible). The result was a highly original and operational hybrid system.
Article body
En parcourant la fresque décrivant le développement des notations chimiques depuis l’alchimie jusqu’à l’époque actuelle, il faut bien constater que l’alchimie n’est pas si lointaine et révolue qu’on se plaît à l’imaginer. Le chimiste d’aujourd’hui vit dans une sorte de musée qui sans cesse le renvoie, de façon subliminale, à un climat symbolique toujours actif. Celui qui, devant les potiquets disposés sur l’étagère poussiéreuse où Morandi les peignait, en leur donnant le nom équivoque de Nature morte, nous fait rêver à tout ce qu’on a pu y placer : onguents, parfums, drogues, potions, poisons… toute une chimie indéfinie et plus ou moins sulfureuse. L’usage familier de tout un vocabulaire spécialisé et traditionnel, fait de mots prononcés sans trop se préoccuper de leur origine, constitue un climat spirituel fortement imprégné par l’alchimie : fiole, matras, bain-marie, fermeture hermétique, alambic, eau régale, vitriol… Mais ce paysage mental est aussi à base de mythologie grecque : mercure, sélénium, saturnisme, irisation, uranium, niobium… ; de folklore : cobalt, nickel, titane… ; de géographie : Bleu de Prusse, germanium, polonium… ; de renvois connotatifs : chlore, vif-argent, tungstène… ; ou simplement d’histoire des sciences : pipette Pasteur, plaque de Pétri, bec Bunsen, Erlen-Meyer… Tout cela ne peut manquer de se refléter dans la notation.
Tout comme l’alchimiste, le chimiste d’aujourd’hui opère des transformations et travaille dans un laboratoire. Il a seulement renoncé au local contigu : l’oratoire. Contrairement au physicien ou au mécanicien, qui manipulent des objets macroscopiques, le chimiste travaille sur des entités inaccessibles directement aux sens : atomes et molécules, ce qui rend ses résultats mystérieux et quasi magiques.
Les systèmes humains de notation graphique sont extraordinairement variés et bien adaptés aux contenus à transmettre. Ainsi, il y a bien peu de points communs entre la notation musicale, les alphabets, la sténographie et les symboles chimiques. Néanmoins, tous ces systèmes ont en commun le fait d’être évolutifs, c’est-à-dire d’être sans cesse remodelés, soit pour remplir plus efficacement leur objectif, soit pour s’adapter à l’évolution de leur contenu.
Les alphabets et les partitions musicales ont à noter des contenus organisés de façon temporelle, alors que les symboles chimiques notent des substances, des entités, des structures statiques. En chimie, le mode de liaison entre le symbole graphique adopté et l’entité dénotée est très variable et a évolué au cours de l’histoire entre deux des principales possibilités classiquement décrites : l’iconisme et la convention symbolique, aboutissant même à des formes hybrides tout à fait singulières.
Il est commode de diviser le panorama des notations (al)chimiques en trois périodes :
l’alchimie ;
Lavoisier, Berzelius, Dalton ;
les notations contemporaines.
I. L’alchimie
L’alchimie n’est pas (ou pas seulement) cet insondable réservoir de mystères que beaucoup veulent y voir. Elle n’est pas non plus cette énorme supercherie ou cette illusion désolante que d’autres dénoncent. Elle n’est pas, enfin, un simple paravent à des activités illicites de faux-monnayeurs ou d’empoisonneurs. Je la vois comme une authentique démarche scientifique qui, vu l’époque, s’appuyait surtout sur l’observation et sur la spéculation, mais qui a beaucoup contribué à créer et à développer, non sans risques, cet outil scientifique nouveau, devenu principal aujourd’hui, qu’est l’expérimentation. Elle constitue une impressionnante tentative de mise en ordre du savoir technique.
Pour comprendre l’alchimie et son symbolisme, il faut se pénétrer des quelques grands principes considérés par elle comme évidents et indiscutables. Tout d’abord le signifiant et le signifié d’une image (abstraite ou non) sont considérés comme formant une seule entité fusionnée, le signe pouvant devenir un équivalent magique du signifié. Cette confiance totale en l’image sera à son comble dans le Mutus Liber (1677-1702), ouvrage constitué de 15 planches sans un seul mot.
Les quatre constantes de la pensée alchimique peuvent être résumées comme suit :
l’univers manifeste une unité fondamentale ;
un réseau étroit de correspondances assure cette unité ;
les principes actifs sont en nombre réduit (2–3–4) ;
le changement résulte de forces antagonistes agissant sur les substances.
On est aussitôt frappé par le fait que sont ainsi formulées, déjà, les idées qui animent encore la science d’aujourd’hui, comme va le montrer un examen plus détaillé de chacune d’elles.
I.1 Unité – Simplicité – Constance
Postuler l’unité, la simplicité et la constance du monde mène à la recherche des « éléments » de ce monde. Le pythagorisme, qui était la théorie des nombres disponible à l’époque, se présente tout naturellement pour expliquer l’unité et la simplicité. La constance, quant à elle, est affirmée malgré l’observation des changements. Elle s’exprime dans le très beau symbole de l’Ouroboros (fig. 1) qui préfigure clairement nos concepts actuels de conservation (de la matière, de l’énergie) et de recyclage. Il est à remarquer que ce symbole est parvenu à synthétiser constance et changement, c’est-à-dire une conception statique et une vision dynamique. De tout temps, et encore de nos jours (Schummer, 2004), les chimistes se sont rangés en deux catégories : ceux qui considèrent leur art comme la science qui identifie et décrit les substances et ceux pour qui la chimie concerne plutôt leurs propriétés réactionnelles. Cette opposition entre substances et processus se retrouve pratiquement dans toutes les disciplines et traduit une grande constante de la cognition : les entités ne peuvent être identifiées que par leurs propriétés, mais les propriétés n’ont pas d’autre siège que les entités. En d’autres termes, elles se définissent l’une l’autre et il n’y a pas lieu de choisir.
I.2 Correspondances
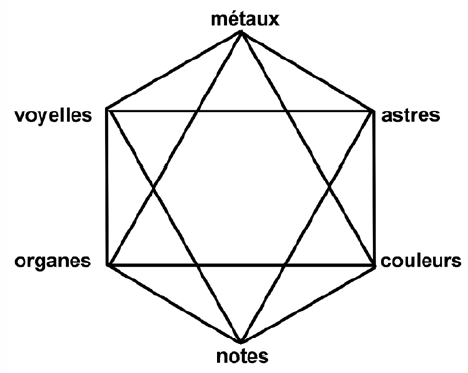
Les correspondances proposées sont innombrables et traduisent une tendance compulsive à voir le monde comme un tissu de relations analogiques, plus ou moins hiérarchisées. L’une d’entre elles subsume toutes les autres et jouit d’un respect unanime : c’est la Tabula Smaragdina, attribuée à Hermès Trismégiste, et qui énonce « Ce qui est en bas est comme ce qui est en haut et ce qui est en haut comme ce qui est en bas ». La permanence de cette idée est visible dans cette image du Rajasthan (xixe siècle, fig. 2) qui montre la terre entre les mondes du haut et du bas, entre Macrocosme et Microcosme. Un des multiples symboles du mercure (fig. 9) dessine de façon très élégante cette union des deux mondes. Garanties par cette correspondance grandiose, de nombreuses correspondances particulières sont alors avancées. Laszlo (2003) figure les principales dans un hexagone (fig. 3), mais il y en a bien d’autres encore. Les correspondances sont généralement fondées sur des analogies (plus rarement sur des contiguïtés) et jouent pleinement sur la symétrie de cette relation. Si la Nature (Macrocosme) est capable d’engendrer, en son sein, comme une mère, des gemmes et des métaux précieux, l’Homme (Microcosme) doit semblablement par son Art pouvoir obtenir des résultats identiques. L’analogie a donc valeur explicative, même si elle porte sur un signe. La version extrême de ce principe est l’acrostiche (voir fig. 4) qui extrait une maxime alchimique du nom d’une substance, le vitriol. Ce rôle central de l’analogie, ciment exclusif de la cohérence du monde, joue en reliant entre eux trois niveaux (Laszlo, 2003) :
le niveau des théories cosmologiques générales ;
le niveau des domaines particuliers et des substances ;
le niveau de l’art (Ars) imitant les processus macroscopiques.
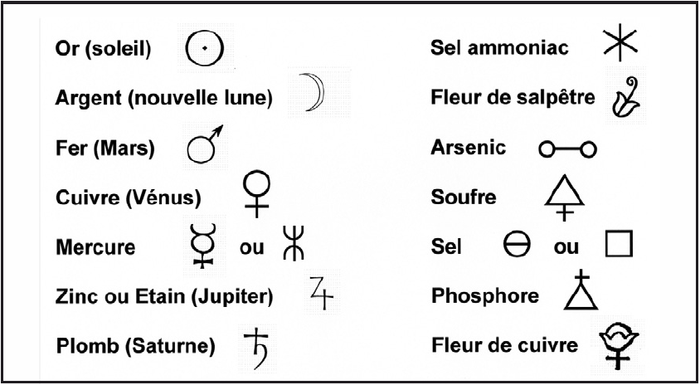
Le cadre idéologique dans lequel se développe cette pensée est celui de l’aristotélisme, du platonisme et du néo-platonisme (Obrist, 2003). Il n’est donc pas étonnant que le symbole alchimique affiche et affirme déjà ces correspondances : on utilisera par exemple le même signe pour désigner la planète Saturne et le métal plomb (fig. 9).
I.3 Simplicité
La réduction du monde à un nombre limité de principes actifs est plus délicate à évaluer. Il semble difficile d’y voir une caractéristique du monde, car c’est plutôt une limitation de la pensée humaine. Le rasoir d’Occam, sous toutes ses formes, et son principe de parcimonie, continue d’accompagner notre réflexion comme un impératif. Pourtant, comme le soulignent brillamment Hoffmann et alii (1997 : 9), cette simplicité ne concerne pas le monde lui-même, qui est ce qu’il est, mais seulement la conception que nous pouvons nous en former vu les limitations de l’esprit humain.
Quoi qu’il en soit, l’alchimie a systématiquement cherché à restreindre le nombre de principes actifs, en hésitant entre 2, 3 et 4, nombres déjà par eux-mêmes affectés d’une forte charge symbolique. Le nombre 7 intervient également, mais plutôt dans les inventaires (7 métaux, 7 planètes, 7 jours de la semaine, 7 merveilles du monde, 7 mers, 7 voyelles grecques…) que comme principe plasmateur.
Les alchimistes ont adopté la quadripartition qui caractérise le monde humain dans les conceptions anciennes. C’est non pas seulement dans la foulée d’Aristote qu’on la trouve, mais aussi dans toutes les civilisations. Elle semble résulter de la symétrie du corps humain (parmi une immense littérature [voir Christinger et alii, 1980 : 13]). Quoi qu’il en soit les alchimistes ont élaboré un diagramme original et ingénieux (fig. 5) pour expliquer, ou justifier, simultanément la correspondance des 4 principes, des 4 éléments et de leurs 4 symboles. Cette figure très rationnelle montre tout d’abord que les 4 principes (chaud/froid et sec/humide) sont opposés par paires et n’existent pas à l’état pur : ils forment une matrice 2 x 2 dans laquelle chaque case combine nécessairement un élément de chaque paire :
N’existant pas à l’état isolé, ils sont un peu, par rapport aux substances qu’ils animent, ce que sont les traits distinctifs vis-à-vis des phonèmes. Mais cette même figure justifie aussi la forme triangulaire retenue pour les symboles des 4 éléments (fig. 6), forme d’ailleurs surdéterminée par des aspects iconiques. Le triangle pointe en haut qui symbolise le feu est une image stylisée de la flamme. Le triangle pointe en bas symbolise l’eau par l’image métonymique d’un entonnoir ou du fond d’une coupe. La barre transversale de l’air et de la terre indique un poids supplémentaire. L’ensemble est parfaitement cohérent, symétrique et binaire.
Il est à peine besoin de rappeler que nous, chimistes d’aujourd’hui, continuons à concevoir notre discipline à travers de semblables dualismes, soit de catégories, soit de forces antagonistes : métaux/métalloïdes, acides/bases, oxydation/réduction, anions/cations, aliphatique/aromatique, électrophile/nucléophile, minéral/organique, oxydes/anhydrides, etc.
Évidemment les alchimistes, qui n’avaient pas encore fait de distinction claire entre un corps pur et un élément[2], ne pouvaient poursuivre cette réflexion que par spéculation… une spéculation soucieuse malgré tout d’appliquer les grandes règles du carré.
Il devenait logique de considérer le monde comme issu de l’action de deux corps primordiaux, vus comme des essences ou des principes plus encore que comme des matières physiques. Le choix des alchimistes arabes s’est porté sur le soufre et le mercure, réduisant à deux les quatre éléments d’Aristote. Leur conjonction semblait en effet à même d’engendrer le monde entier puisque le soufre participe du chaud et du sec, alors que le mercure participe du froid et de l’humide. Or, le jeu des analogies fait aussi du soufre un élément actif et masculin, alors que le mercure est vu comme passif et féminin. Ils sont parfois métaphoriquement décrits comme l’épée et son fourreau. La sexualisation des composants de l’univers devait nécessairement apparaître et engendrer un vaste réseau d’analogies (la terre-mère, etc.) susceptible même de se combiner à l’opposition jour/nuit (le soleil et la lune, voir aussi plus loin Mars et Vénus). Ultérieurement, sous l’influence de Paracelse (1493-1541), un troisième terme fut adjoint : le sel, élément fixe et neutre, qui reste inchangé dans le feu. Par ce troisième terme, l’on complète une sorte d’axe sémantique vertical, au sens de Greimas, qui non seulement établit l’opposition fondamentale, mais indique le moyen de la « médier ».
Ces déterminations générales étant posées, on peut examiner plus en détail le répertoire des symboles alchimiques. On y découvrira non pas une organisation d’ensemble cohérente, mais seulement quelques sous-ensembles parfaitement structurés, ou des principes de codage tendanciels. Assez naturellement se fait jour une similitude avec les règles morphosyntaxiques qui régissent le langage. On peut distinguer trois groupes de symboles : pour les appareils, pour les opérations, pour les substances.
Les signes désignant l’appareillage seront tout naturellement en majorité iconiques et présenteront une image stylisée de l’appareil (fig. 7). De ce fait, ils ne donnent pas lieu à une grande inventivité. Tout autre est le cas des opérations, car il s’agit là de représenter un processus, ou un mouvement, par une image fixe (fig. 8). Les alchimistes avaient dénombré une douzaine d’opérations, dont un grand nombre sont toujours couramment pratiquées aujourd’hui : distillation sous reflux, cristallisation et recristallisation, sublimation, coagulation, précipitation, dissolution, calcination[3]…
La sublimation, qui est le passage direct de l’état solide à l’état gazeux (manifesté par l’eau sous certaines conditions, et aussi par le camphre), avait de quoi intriguer. Le signe employé, à la fois métaphore et emblème, était parfois un oiseau (Laszlo, 2003). Le plus souvent, cependant, on le représentait comme l’inverse de la précipitation, en orientant la boucle du symbole vers le haut ou vers le bas selon la direction physique évidente du processus. Le broyage aurait pu être représenté par l’image d’un pilon et d’un mortier, mais il a semblé plus parlant d’utiliser une spirale, soit la trace du mouvement imposé au pilon dans le mortier. Pour la calcination, on a retenu le signe du feu, avec en son centre le petit résidu qu’il laisse subsister.
L’examen du corpus des signes employés par les alchimistes pour désigner les substances, avec lesquelles et sur lesquelles ils travaillaient, est de loin le plus intéressant du point de vue sémiotique. En effet, à l’échelle macroscopique, ce sont des poudres, des liquides, des solides amorphes, des gaz, qui ne sont pas représentables iconiquement. Les figures 9 et 10 montrent la variété des méthodes d’appariement du signifiant au signifié. On peut en dégager les observations suivantes :
le signe est à la fois un moyen mnémotechnique et une abréviation, une sorte de sténographie permettant de présenter des processus complexes sans avoir à se perdre dans des descriptions particulières ;
le signe a en même temps pour fonction de manifester, ou de rappeler visuellement, la vaste théorie anthropocosmique qui subsume les différentes facettes de l’activité des alchimistes (physique, psychique, magique, idéologique…). En effet, et c’est une différence capitale par rapport au code linguistique, cet aspect-là est vu mais non lu ni prononcé. Les signes alchimiques fonctionnent simultanément sur les deux plans, conjoignant les avantages des deux systèmes, et constituent donc d’authentiques signes intersémiotiques[4] ;
les signes sont, dans la plus grande mesure possible, motivés. Le signe graphique, imagé, est toujours préféré au signe alphabétique. On ne recourt à ce dernier que si aucune formule graphique suffisamment motivée et simple à tracer n’a pu être trouvée. La recherche du secret peut également avoir joué. Exceptionnellement, on trouve des signes hybrides (fig. 12) ;
souvent le signe d’une substance est motivé par la fonction qu’on lui attribue dans le système spirituel ou conceptuel des alchimistes, ou par les liaisons qu’on lui prête avec un processus analogue, plutôt que par les propriétés intrinsèques et objectives de ladite substance ;
une correspondance biunivoque, terme à terme, n’a que rarement été réalisée : le même signe peut renvoyer à plusieurs corps distincts, et le même corps recevoir de nombreux signes différents (fig. 11), sortes de synonymes ;
un souci de cohérence et de rationalité ressort néanmoins clairement de la syntaxe employée pour modaliser un signe donné, soit en le combinant à un autre signe, soit même en lui adjoignant des morphèmes sans existence indépendante (fig. 12 et 13) ;
sur le plan graphique, ont été exploitées pratiquement toutes les possibilités combinatoires : superposition, intersection, inclusion, tangence[5].
II. Lavoisier, Berzelius, Dalton
La pensée alchimique formait un tout très monolithique et peu évolutif. Partagée entre une spéculation philosophique ou spirituelle devenue dogmatique et l’expérimentation véritable, elle n’a pas pu incorporer facilement les acquis expérimentaux qui s’accumulaient au cours des siècles[6]. L’histoire laisse apercevoir plusieurs cycles caractérisés par une alternance entre un vif intérêt pour l’activité expérimentale et sa désaffection au profit de la tendance spéculative et mystique. La Grande Encyclopédie du xviiie siècle reproduit encore les symboles des alchimistes, quoique en essayant de représenter certaines relations entre corps chimiques grâce à un nouveau dispositif : la mise en tableau. Le processus devait inéluctablement déboucher sur une rupture qui fut une véritable révolution. On s’accorde à en attribuer la paternité à Lavoisier et à Guyton de Morveau qui, en 1787, proposèrent une réforme de la nomenclature (Baudet, 2004 :137). La révolution devint effective et définitive en quelques décades et son aspect le plus visible fut l’abandon des symboles de l’alchimie au profit d’une notation conçue comme neutre, c’est-à-dire libérée de tout a priori théorique, et censée laisser aux chercheurs toute liberté dans la conception de leurs expériences.
Le système définitif ne vit le jour qu’en 1814 dans la version mise au point par Berzelius (1779-1848). Le modèle choisi, inspiré tout naturellement du langage, a la forme d’un code à une lettre majuscule (l’initiale du nom de la substance : I pour iode) ou à deux lettres, une majuscule suivie d’une minuscule (pas nécessairement les deux premières : Co pour cobalt, mais Hg pour mercure, anciennement appelé hydrargyrum). Assorti de nombres décalés sur la ligne (d’abord en exposant, plus tard en indice), le système permettait une désignation économique, claire et univoque de toute substance, moyennant quelques règles additionnelles de syntaxe – qui, d’ailleurs, ont changé par la suite. C’est donc un langage construit, sans redondance, premier pas vers une représentation des corps chimiques par un système formel au sens logique du terme, plus proche d’un code que d’un langage par sa « bijectivité ».
Inspiré par le langage et lui empruntant ses signes (aucun signe nouveau ne fut créé), le code de la chimie ne produisait cependant pas de noms. Les formules peuvent certes se lire et se prononcer (par exemple Fe2(SO4)3 = effe-é-deux-esse-o-quatre-trois-fois), mais le nom de la substance est « sulfate ferrique ». La formule ne contient plus que des informations objectives, tirées des connaissances acquises sur les diverses substances. Elle se préoccupe avant tout de la proportion des divers composants, ici le fer, le soufre et l’oxygène.
Curieusement, cette abstraction non directive allait soulever des résistances et des critiques, résumées comme suit par David Knight (2003), qui parle d’« austérité lavoisienne » :
on a « exalté la compréhension » mais en « déprimant l’imagination » ;
le symbole chimique est devenu une simple sténographie ;
le système qui a prévalu (Berzelius) est le moins suggestif parmi ceux proposés ;
le système est dépourvu de la redondance « si utile dans le langage » ;
le système est incapable de noter les processus.
Telle n’est pas l’opinion d’Ursula Klein (2001) qui démontre, faits à l’appui, que ce système a permis de significatives avancées entre 1820 et 1850 environ, notamment grâce aux travaux de Dumas. Elle voit dans les formules écrites, même si elles ne se prétendent pas une « image » des molécules, au sens iconique du terme, un puissant moyen d’affiner des raisonnements théoriques : ce sont des outils de papier (paper tools). Une part de leur efficacité provient justement de ce qu’ils restent abstraits et non directifs. On trouvera par exemple dans son étude la description des recherches de Dumas sur la production du chloral à partir d’alcool et de chlore : c’est en utilisant le système Berzelius que Dumas en vient à proposer le concept de substitution, appelé à devenir un concept-clé de la chimie moderne.
Les succès obtenus découlent essentiellement de l’incorporation de nombres dans la notation. Armés d’un puissant principe de conservation de la matière, les chimistes du temps, qui étaient des chimistes de la balance, pouvaient désormais quantifier leur travail : soit prévoir les quantités de produits issus d’une réaction donnée, soit déduire la formule des produits formés à partir de leur quantité. Il est donc logique que leurs équations utilisent le signe = et il est vain de leur reprocher une incapacité à noter les processus.
Les chimistes de l’époque, surtout préoccupés de stoechiométrie, n’avaient pas encore développé ce qui allait devenir la stéréochimie, mais ils ne s’en posaient pas moins la question de la disposition relative des atomes dans une molécule, et leur système de notation reflète ce souci. La grande absente du système est, semble-t-il, la liaison chimique (le « crochet » des futurs « atomes crochus »). En fait, elle est indiquée autrement, et subtilement, en trois degrés :
si deux symboles[7] sont apposés, c’est qu’un lien les unit : KCl ;
si un atome est lié à un groupe d’atomes, cette distance supplémentaire est marquée par des parenthèses qui établissent ainsi une hiérarchie dans l’emboîtement des parties : Ca(HCO3)2 ;
enfin, la présence d’eau de cristallisation (ou d’hydratation) est indiquée en la séparant par un point : Al2(SO4)3 . 18 H2O qu’on peut aussi écrire Al2(SO4)3 . 18 aq (prononcer « aqua »).
Dans sa version la plus fruste, la notation se contente de faire l’inventaire quantitatif des atomes, sans aucunement les regrouper. C’est ce qu’on appelle une formule brute : par exemple le camphre = C10H16O. Il serait totalement erroné de penser que ce type de formule n’a plus aucun intérêt. Démonstration en est faite par la formule de la biomasse ou « biomôle » (Edeline, 1993) C5H7NO2. Les biochimistes préoccupés de la nutrition et de la croissance des êtres vivants se sont demandé comment formuler une expression quantitative unissant des aliments chimiquement bien définis (des sucres, des graisses…) à une matière vivante d’énorme complexité. La réponse a consisté en l’analyse élémentaire de centaines de cultures (bactériennes surtout), qui s’est révélée remarquablement uniforme, et pouvait se traduire par une formule brute dans laquelle on donnerait la valeur 1 à un composant numériquement mineur mais néanmoins essentiel : l’azote. Sur cette base, la biomôle peut se formuler, avec une suffisante approximation, par C5H7NO2. Comme dans la matière vivante, le rapport N:P (rapport des concentrations en azote N et en phosphore P) est constant ; il n’est pas nécessaire d’inclure P dans la formule, ce qui maintient petits les coefficients. Cette formulation a rendu d’immenses services en prévoyant de façon quantitative les besoins métaboliques des biomasses industrielles. Exemple d’application :
Signalons encore une variante préconisée par les cristallographes et les minéralogistes, qui notent les minéraux naturels sous la forme d’oxydes, d’anhydrides et de molécules d’eau (cette dernière étant aussi, en dernière analyse, de l’oxyde d’hydrogène). Cela donne un système très cohérent mais avec lequel il faut se familiariser. Toutes les sous-entités sont séparées par des points :
L’idée sous-jacente[8] était que ces substances, d’origine géologique ignée, ne pouvaient être qu’à l’état oxydé. De telles formules suggèrent néanmoins aussi une disposition spatiale, qu’exploite le cristallographe, et attirent doublement l’attention sur les proportions entre composants. On a voulu étendre ce type de notation à des substances autres que les minéraux naturels, mais sans réel succès, par exemple : Ca(OH)2 devait être noté CaO. H2O, et H2SO4 devenait SO3. H2O.
On constate donc que la flexibilité du système est malgré tout assez grande, et que les reproches adressés au système de Berzelius sont très exagérés.
Il est cependant exact que d’autres systèmes étaient en compétition, en particulier celui de Dalton (1766-1844), instituteur à Manchester, chimiste autodidacte et fort inventif. Son système consiste à représenter tous les atomes (qu’il appelait « particules » ou « corpuscules ») par un cercle, en attribuant à ce cercle un diamètre correspondant à la dimension supputée de l’atome (fig. 14 et 15). L’atome était identifié par diverses formes tracées à l’intérieur du cercle : barres verticales ou horizontales, croix, zigzag, etc. On relève treize combinaisons de ce type, au-delà desquelles Dalton, pour éviter la confusion, a recouru à l’initiale du nom anglais de la substance. Ceci donne I pour Iron ou S pour Silver et peut engendrer des confusions pour un lecteur français, qui comprendrait iode et soufre. Ce problème de communication très réel n’a pu être surmonté que par un accord international, basé cette fois sur les noms latins (comme recommandé par Berzelius) : Sn de stannum pour étain, K de kalium pour potassium, Sb de stibium pour antimoine, etc. Le système de Dalton n’encourait pas le reproche d’étouffer l’imagination : les figures 15 et 16 montrent au contraire qu’il la dirigeait un peu trop et menait à suggérer des configurations spatiales pour les molécules… malheureusement souvent erronées ou impossibles. Ce système, au grand dépit de son inventeur, ne s’est pas popularisé.
III. Notations contemporaines
Les progrès rapides de la chimie, qui abordait désormais les molécules organiques, ont fini par faire apparaître de sérieux problèmes de notation. C’est seulement vers 1850 que la stéréochimie s’est développée et que ces insuffisances sont apparues. Des améliorations devenaient indispensables, et elles se sont révélées possibles.
III.1 Liaison chimique
La reconnaissance de la nature exacte des forces qui unissent les atomes rendait indispensable leur notation explicite et différenciée. La liaison chimique va se noter par un petit trait, qui s’écrit mais ne se prononce pas. Les doubles et triples liaisons se noteront par autant de traits parallèles[9]. Le fait que jusqu’à six liaisons peuvent aboutir au même atome a obligé à renoncer à la linéarité initiale pour recourir (dans un premier temps) à des graphismes à deux dimensions : nouveau trait visible mais imprononçable (voir la fig. 17 pour quelques exemples). La reconnaissance du caractère électronique des liaisons a aussi donné (fig. 18) des formules où les électrons sont représentés par de petits cercles ou de petites croix. On pouvait ainsi aisément vérifier si la structure possédait une enveloppe stable, constituée de paires ou d’octets, et si elle respectait l’électroneutralité.
III.2 Structures cycliques
Un problème resté célèbre, parce qu’il était rétif à toute transcription selon le système orthodoxe, est celui de la formule du benzène, résolu par Kekulé en 1865. Le nom de cette substance renvoie à son origine (le benjoin), ce qui peut être utile mais ne renseigne nullement sur sa configuration stérique. La figure 19 montre la formule brute du benzène, seule donnée indiscutable au départ. Elle montre ensuite diverses configurations suggérées[10], la formule définitivement acceptée, ainsi que plusieurs de ses notations équivalentes. On voit que seule une représentation bidimensionnelle permet de comprendre cette structure, encore que l’écriture contraigne à placer les doubles liaisons en des endroits déterminés alors qu’on sait qu’elles n’ont pas de localisation préférentielle… Toute la chimie des molécules dites aromatiques découle de cette découverte.
III.3 Distinction des isomères
Un second problème se montra insoluble même par ce qu’on a appelé des « formules déployées planes » : celui des énantiomorphes. Le cas le plus simple, et qui apparut le premier (en 1870), est celui de l’acide lactique (fig. 17). L’atome de carbone, supposé au centre d’un tétraèdre, permettait deux et seulement deux configurations qu’il importait de distinguer. Il a fallu pour cela établir de nouvelles conventions graphiques inspirées des règles de la perspective (Baudet, 2004 : 200), et qui permirent de représenter la troisième dimension. Elles s’énoncent comme suit :
les liaisons chimiques de la partie frontale (proximale) d’une molécule sont représentées en traits épais ;
les liaisons de la partie lointaine (distale) sont en traits minces ;
les liaisons entre un atome situé en avant du plan de la figure et un autre situé sur ce dernier sont représentées par un triangle effilé noir, dessiné comme s’il était vu en perspective ;
pour les liaisons entre un atome situé sur le plan de la figure et un autre situé derrière ce dernier, on adopte la même convention mais avec un triangle effilé blanc (parfois on lui préfère un trait tireté : système wedge-dash).
Ce système est hybride dans la mesure où il conserve les notations alphabétiques : chacune d’entre elles condense le renvoi à un atome, sans expliciter aucune de ses caractéristiques.
La question des énantiomorphes n’était pas, elle non plus, anodine. Ils peuvent avoir un comportement optique opposé (déviation du plan de polarisation de la lumière), et il arrive qu’un seul de ces isomères soit présent dans la matière vivante.
Dans le but de faciliter encore l’exploitation heuristique des modèles représentatifs, on a mis en circulation des « modèles physiques », faits de boules colorées de diamètre variable, de tiges et de ressorts ajustables. Leur description sort du cadre de la présente étude, de même que celle des configurations obtenues aujourd’hui par CAO (conception assistée par ordinateur), et qui peuvent s’attaquer à des molécules aussi complexes que des protéines ou des ADN, en précisant même leurs enroulements les plus probables.
IV. Conclusions
L’évolution globale ci-dessus retracée accuse un mouvement pendulaire par lequel on est passé d’une notation à caractère iconique ou motivé très marqué à un système parfaitement biunivoque et symbolique (au sens peircien du terme), pour revenir à une réintroduction de plus en plus large de l’iconisme. Les trois phases partagent le même souci sémiotique : désigner les corps chimiques par des signes, mais leur qualité heuristique est totalement différente, et même opposée. En effet, il ne s’agit pas du même iconisme. Celui de l’alchimie peut être qualifié d’illustratif car ses images illustrent une théorie préexistante, en grande partie spéculative, que l’on se contente de confirmer à travers les signes. La seconde phase se veut dépourvue d’iconicité, ce qui lui a permis, presque paradoxalement (comme l’a brillamment montré U. Klein, 2001a et b) d’asseoir la chimie sur des bases quantitatives et descriptives plus fermes. Quant aux perfectionnements successifs apportés ultérieurement aux formules berzeliennes, on a vu qu’ils portent essentiellement sur la représentation de la seconde puis de la troisième dimension, dans le but de fournir des images de plus en plus satisfaisantes de la configuration spatiale des molécules. Mais s’agit-il vraiment d’iconisme ? Ces signes seraient iconiques de quoi ? Personne n’ayant jamais vu une liaison chimique, il ne peut y avoir ressemblance vérifiable entre une molécule et le signe qui la représente. On dira plutôt que ces signes représentent nos hypothèses interprétatives, de façon visuelle et selon des conventions d’écriture. On conçoit en effet qu’une liaison chimique ne peut avoir qu’un lointain rapport avec un petit segment de ligne droite, et des représentations plus fidèles à ce qu’on sait de leur nature physique mènent à des tracés comme ceux de la figure 20. Pour sa part, Schummer (1996) estime que la notation chimique n’est ni conventionnelle (symbolique), ni indicielle, ni iconique : il revendique pour elle un quatrième régime, spécifique, qu’il nomme Strukturzeichnungen et qui s’exploite par une interprétation analogique.
Laszlo (2000a) résume fort bien les trois positions possibles : on peut raisonner sur des textes, sur des concepts ou représentations mentales, ou sur des modèles. La possibilité heuristique d’assister la recherche en travaillant sur des modèles visuels, en vue de planifier des expériences cruciales ou d’éviter des démarches inutiles, a fait l’objet de nombreuses réflexions récentes (Hoffmann et Laszlo, 1991 ; Schummer, 1996 ; Del Re, 1998 ; Weininger, 1998 ; Mainzer, 1999 ; Francoeur, 2000 ; Laszlo, 2000a ; Ramberg, 2000 ; Zeidler, 2000). Les chimistes semblent se partager en adversaires et en partisans des modèles matériels, et ce débat n’est qu’un aspect du débat plus général sur la nature du réel. Comme selon toute vraisemblance, celle-ci nous restera à jamais inconnaissable, il semble logique de se résigner à raisonner sur des modèles qu’on s’en fait, à condition de rester conscients que ce ne sont que des modèles, d’éviter de leur accorder une valeur ontologique, et de se méfier de considérations esthétiques (dont le rasoir d’Occam) qui n’ont rien à voir avec la problématique.
La fonction heuristique des signes consiste à permettre un aller-retour constant entre les signes et l’expérimentation, dans un mouvement qui n’est pas sans rappeler le binôme assimilation/accommodation de Jean Piaget.
Figures 1 à 20
Figure 1
L’Ouroboros
Figure 2
La correspondance universelle
Figure 3
Les correspondances particulières (d’après Laszlo, 2003)
Figure 4
Stolcius (1624) : acrostiche de VITRIOL
Figure 5
Le système des éléments (Liungman, 1991)
Figure 6
Les quatre éléments
Figure 7
Quelques symboles alchimiques courants. Les appareils.
Figure 8
Quelques symboles alchimiques courants. Les opérations.
Figure 9
Quelques symboles alchimiques courants. Les substances.
Figure 10
Exemples de motivation des signes : iconisme, métonymie, emblème...
Figure 11
Absence d’univocité des notations alchimiques.
Figure 12
Syntaxe graphique (parfois hybride !).
Figure 13
Existence de morphèmes.
Figure 14
Symboles chimiques selon Dalton (1806).
Figure 15
Dalton Schémas proposés pour la configuration de différents corps
Figure 16
Dalton Exemple d’utilisation heuristique d’une syntaxe iconique.
Suggère une explication de la fluidité de l’eau par rapport à la glace
de la structure hexagonale du cristal de neige.
Figure 17
Problème de l’acide lactique (1870 sq).
Figure 18
Théorie électronique de la valence le doublet et l’octet (apparition de l’hybridité).
Figure 19
Problème de la représentation du benzène.
Figure 20
Quelques représentations contemporaines de la molécule d’eau.
Appendices
Note biographique
Francis Edeline
Ingénieur chimiste, Francis Edeline a publié de nombreuses études sur le symbolisme et sur la poésie, ainsi que des travaux de sémiotique. Auteur de monographies sur Ian Hamilton Finlay (1977) et sur Pierre Garnier (1982), ainsi que de Vocaliques (1987), un essai sur les voyelles. Il a dirigé un numéro spécial des Cahiers internationaux de symbolisme consacré à l’Herméneutique du Mandala (1984). En préparation : L’Intersémiotique et Les Voies du symbole. Membre du Groupe µ depuis sa fondation, avec lequel il a publié notamment : Rhétorique générale (Larousse, 1970 ; Seuil, 1982, trad. en 8 langues) ; Rhétorique de la Poésie (Complexe, 1977 ; Seuil, 1990, trad. en roumain) ; Traité du signe visuel (Seuil, 1991, trad. en espagnol, en allemand et en italien) ; ainsi que de nombreux articles.
Notes
-
[1]
La présente étude concerne la chimie en tant que système de signes. Par conséquent, on n’y trouvera pas un aperçu historique de la filiation des idées ou des découvertes. Par contre, pour expliquer certains signes, il sera souvent nécessaire de faire appel au symbolisme spirituel ou mythologique sous-jacent, ce qui aura pour inconvénient d’obliger à utiliser conjointement le mot symbole dans ses deux sens. Nous appellerons symbole peircien une association conventionnelle et arbitraire entre signifiant et signifié. Dans les autres cas, il s’agira d’associations libres (analogiques le plus souvent) toujours pensées comme impliquant des liaisons motivées profondes et universelles.
-
[2]
Pas plus qu’entre mélange et combinaison et, a fortiori, entre atome et molécule.
-
[3]
Plusieurs de ces opérations sont plutôt physiques que chimiques, mais là non plus la distinction n’était pas encore clairement faite… et d’ailleurs, cette distinction s’estompe à nouveau aujourd’hui.
-
[4]
Pour une première présentation de ce concept, voir Edeline (1999). Un ouvrage détaillé sur le sujet, couvrant la blason, le mandala, le poème sémiotique, le tatouage, le rébus, l’alphabet figuré, le monogramme, le calligramme, etc., est en préparation.
-
[5]
Ce sont exactement les mêmes que l’on retrouve dans l’élaboration d’un autre corpus intersémiotique : les monogrammes (Edeline, 2006).
-
[6]
Neuf siècles approximativement.
-
[7]
À partir de maintenant, le mot symbole désigne une convention pure.
-
[8]
Héritée de la théorie dualiste en vigueur au début du xviiie siècle (Baudet, 2004 :166).
-
[9]
Le trait a même pu être pointillé, comme dans la théorie de la valence partielle de Thiele.
-
[10]
Au cours de discussions souvent âpres, comme le différend entre les chimistes Berthelot et Kekulé (xixe siècle).
Références bibliographiques
- Baudet, J. [2004] : Penser la matière, Paris, Vuibert.
- Christinger, R., J. Eracle et P. Solier [1980] : La Croix universelle, Paris, Dervy Livres.
- Del Re, G. [1998] : « Ontological status of molecular structure », HYLE (International Journal for Philosophy of Chemistry), vol. 4, no 2, 81-103.
- Edeline, F. [1993] : L’Épuration biologique des eaux, Paris, Lavoisier ;
- Edeline, F. [1999] : « L’Intersémiotique », dans J. Bernard et G. Withalm, Sémioses dans les systèmes complexes, 7° Congrès de l’Association internationale d’études sémiotiques, Université de Technologie de Dresde ;
- Edeline, F. [2006] : « Le monogramme et le conflit des codes », dans M. G. Dondero et N. N. Paglianti (dir.), Syncrétismes, Limoges, PULIM, 33-64 ;
- Francoeur, E. [2000] : « Beyond dematerialization and inscription – Does the materiality of molecular models really matter? », HYLE, vol. 6, no 1, 85-97.
- Hendry, R. F. [1999] : « Molecular models and the question of physicalism », HYLE, vol. 5-2, 143-160.
- Hoffmann, R. et P. Laszlo [1991] : « Representation in chemistry », Angewandte Chemie International Ed. in English, vol. 30, no 1, 1-16.
- Hoffmann, R., V. I. Minkin et B. K. Carpenter [1997] : « Ockham’s razor and chemistry », HYLE, vol. 3, no 1, 3-28.
- Klein, U. [2001a] : « Berzelian formulas as paper tools in early nineteenth-century chemistry », Foundations of Chemistry, vol. 3, 7-32 ;
- Klein, U. [2001b] : « Paper tools in experimental cultures », Studies in History and Philosophy of Science, vol. 32, no 2, 265-302.
- Knight, D. [2003] : « Exalting understanding without depressing imagination », HYLE, vol. 9, no 2, 171-189.
- Laszlo, P. [2000a] : Miroir de la chimie – Le camphre et sa formule, Paris, Seuil, coll. « Science ouverte » ;
- Laszlo, P. [2000b] : « Playing with molecular models », HYLE, vol. 6, no 1, 85-97 ;
- Laszlo, P. [2003] : Qu’est-ce que l’alchimie?, Paris, Hachette, coll. « Littératures ».
- Liungman, C. [1991] : Dictionary of Symbols, Santa Barbara (CA), ABC-Clio.
- Mainzer, K. [1999] : « Computational models and virtual reality – New perspectives of Research in Chemistry », HYLE, vol. 5, no 2, 117-126.
- Mestrallet-Guerre, R. [1981] : Communication, linguistique et sémiologie – Contribution à l’étude de la sémiologie des systèmes de signes de la chimie, Barcelone, Universitat Autonoma, Faculté des Lettres.
- Obrist, B. [2003] : « Visualization in medieval alchemy », HYLE, vol. 9, no 2, 131-170.
- Ramberg, P. J. [2000] : « Pragmatism, belief, and reduction – stereoformulas and atomic models in early stereochemistry », HYLE, vol. 6, no 1, 35-61.
- Read, J. [1959] : De l’alchimie à la chimie, Paris, Arthème Fayard.
- Schummer, J. [1996] : « Zur Semiotik der chemischen Zeichensprache: Die Repräsentation dynamischer Verhältnisse mit statischen Mitteln », dans P. Janich et N. Psarros (dir.), Die Sprache der Chemie, Wurtzbourg, Königshausen & Neumann, 113-126 ;
- Schummer, J. [1998] : « The chemical core of chemistry I : A conceptual approach », HYLE, vol. 4, no 2, 129-162 ;
- Schummer, J. [2004] : « Substances versus reactions », HYLE, vol. 10, no 1, 3-4.
- Weininger, S. J. [1998] : « Contemplating the finger : Visuality and the semiotics of chemistry », HYLE, vol. 4, no 1, 3-27.
- Wu, H.-K., J. S. Krajcik et E. Soloway [2000] : « Using technology to support the development of conceptual understanding of chemical representations », dans B. Fishman et S. O’Connor-Divelbiss (dir.), Fourth International Conference of the Learning Sciences, Mahwah (NJ), Erlbaum, 121-128.
- Zeidler, P. [2000] : « The epistemological status of theoretical models of molecular structure », HYLE, vol. 6, no 1, 17-34.
List of figures
Figure 1
L’Ouroboros
Figure 2
La correspondance universelle
Figure 3
Les correspondances particulières (d’après Laszlo, 2003)
Figure 4
Stolcius (1624) : acrostiche de VITRIOL
Figure 5
Le système des éléments (Liungman, 1991)
Figure 6
Les quatre éléments
Figure 7
Quelques symboles alchimiques courants. Les appareils.
Figure 8
Quelques symboles alchimiques courants. Les opérations.
Figure 9
Quelques symboles alchimiques courants. Les substances.
Figure 10
Exemples de motivation des signes : iconisme, métonymie, emblème...
Figure 11
Absence d’univocité des notations alchimiques.
Figure 12
Syntaxe graphique (parfois hybride !).
Figure 13
Existence de morphèmes.
Figure 14
Symboles chimiques selon Dalton (1806).
Figure 15
Dalton Schémas proposés pour la configuration de différents corps
Figure 16
Dalton Exemple d’utilisation heuristique d’une syntaxe iconique.
Figure 17
Problème de l’acide lactique (1870 sq).
Figure 18
Théorie électronique de la valence le doublet et l’octet (apparition de l’hybridité).
Figure 19
Problème de la représentation du benzène.
Figure 20
Quelques représentations contemporaines de la molécule d’eau.