Article body

1. Introduction : Pourquoi Granger ?

Deux qualificatifs sont généralement retenus pour caractériser l’oeuvre de Gilles-Gaston Granger : « épistémologie comparative », et « philosophie rationaliste ». Dans la lignée de deux autres philosophes français de son époque : Martial Gueroult et Jules Vuillemin, Granger a vu dans l’épistémologie comparative un moyen d’instaurer un dialogue constructif entre des théories distinctes, voire même de rapprocher sciences naturelles et sciences sociales à partir d’un critère de constitution commun : leur structure. Cela étant, Granger n’a proposé aucune classification des théories analogue à celle de Vuillemin. Il n’a pas non plus développé l’idée d’une « vérité philosophique » interne à de prétendus systèmes de pensée clos, comme le voulait le projet de « dianoématique » de Gueroult.

Que peut-on trouver de commun chez ces trois philosophes français, malgré tout ? Sans doute leur insistance sur le rôle structurant du langage dans la constitution de la pensée rationnelle. Que faut-il retenir des recherches philosophiques propres à Granger, lui qui, avec les deux philosophes susnommés et Louis Rougier puis Jacques Bouveresse et Jean-Louis Gardies, a introduit et promu en France le courant anglo-saxon de la philosophie dite « analytique » ? D’une part, que la signification de la négation dépend essentiellement de la structure de l’objet auquel elle s’applique. D’autre part, que cette structure n’est pas donnée a priori mais résulte d’un travail de structuration lié au cheminement intellectuel du théoricien. Pourrait-on parler ainsi d’une philosophie de la logique propre à Gilles-Gaston Granger : une « philosophie du style logique pluraliste » ? Prétendre faire de Granger un précurseur du pluralisme logique serait toutefois une erreur et pourrait donner l’impression d’un coup de force intellectuel de la part des logiciens modernes. Il s’agira plus modestement ici de mettre en application cette philosophie que Granger a promue et que Mulligan (1991, p. 115) a décrite en ces termes :

Quand on demande à un philosophe sur quoi il travaille, un analyste répondra par l’énoncé d’un problème, un continental par un nom propre.

La philosophie de la logique de Granger sera condensée dans ce qui suit à travers trois notions fondamentales : la forme, qui permet à l’auteur de singulariser la logique comme le domaine le plus formel de toutes les disciplines scientifiques ; l’objet logique, qu’il considère comme « vide » ou sans aucune propriété dans Granger (2001) ; la négation, qui nous servira d’opérateur caractéristique afin de souligner l’importance de la notion de structure dans le critère de logicité de Granger.

Notre lecture qui suit consistera à soutenir la thèse centrale de Granger, selon laquelle la logique porte sur un objet vide de tout contenu ou « überhaupt » (l’expression apparaît dans Granger 1994), tout en lui associant une direction différente et favorable au pluralisme logique. Dans un premier temps, l’auteur prolonge l’idée de Gonseth (1937) selon laquelle la logique constituerait une « physique de l’objet quelconque » ; en refusant ainsi le caractère a priori des vérités logiques, Granger s’oppose tout autant à l’approche transcendantale de la raison kantienne qu’à l’attitude fondationnaliste des empiristes logiques dans le processus de compréhension des objets. Dans un deuxième temps, un système logique doit satisfaire trois méta-propriétés principales : la décidabilité, qui exige l’existence d’une procédure effective afin de déterminer la signification d’une formule du système ; la complétude, en vertu de laquelle toute proposition vraie doit être déductible à l’intérieur du système ; la consistance, qui exige la non-contradiction du système. C’est sur la base de cette triple exigence que Granger (2001) va considérer un seul et unique système formel comme proprement logique : la logique des propositions classique, dans la mesure où la logique des prédicats n’est pas décidable et renverrait déjà à des objets d’étude particuliers. Le critère technique de la décidabilité s’ajoute ainsi au critère philosophique de l’objet sans qualités pour produire une philosophie de la logique singulière.

Dans un troisième temps, notre contribution principale consistera à affirmer que l’objet propre de la logique peut avoir une qualité « quelconque » sans en être dépourvu absolument : c’est le mécanisme opératoire qui donne sa spécificité à la logique, sans que celle-ci doive se réduire à porter sur un objet sans structure. La confusion entre objet quelconque et objet simple sera corrigée plus loin et conduira à une approche multivalente, opératoire et pluraliste de la logique.

Voyons d’abord à quels problèmes la philosophie de Granger fournira l’occasion de s’attaquer, dans ce qui suit. Le cas de la négation constituera un premier cas particulier pour manifester cette théorie philosophique de l’objet vide, avant d’aborder plus en détail la nature de cet objet logique.

2. La négation selon Granger

Nous venons de voir que la non-contradiction constitue un critère de logicité fondamental. Si tel est le cas, alors que faire notamment de la « logique » paraconsistante et que doit signifier la constante logique de la négation selon Granger ? Dans son analyse du concept de contradiction, celui-ci (1988) formule deux types de distinction pour caractériser la négation. La première oppose une négation « totale » formatrice d’énoncés contradictoires et une négation « partielle » formatrice d’énoncés contraires, parmi les « énoncés aristotéliciens de type canonique ». Il s’agit ici de la distinction entre l’universelle et la particulière, et Granger considère que ces négations spécifient dans une certaine mesure la nature des objets sur lesquels elles portent. Lorsque, en revanche, la négation ne spécifie pas son objet et porte sur un énoncé dont le contenu est ignoré, Granger (1988, p. 40) la qualifie de formelle et en distingue deux sortes : la négation « radicale » et les autres, les négations « particulières ». Il s’explique ainsi :

Nous appelons « négation radicale » celle qui est exprimée par le foncteur de vérité ; « radicale » doit s’entendre au sens de : indépendante de la nature de l’univers des objets. La négation s’applique alors à des formes d’objets vides.

Cette distinction entre une négation « formelle » et une autre qui ne l’est pas peut d’ores et déjà paraître contestable : la nature des objets importe peu pour Aristote, ils peuvent être remplacés par de simples classes tout à fait abstraites, et la théorie des oppositions s’applique à bien d’autres types d’objets abstraits que les propositions universelles et particulières : modalités, attitudes propositionnelles, opérateurs arithmétiques, couleurs, etc[2]. C’est l’isomorphie structurelle entre les formules auxquelles la négation s’applique qui, dans tous ces cas de figure, permet de distinguer par exemple une relation contradictoire d’une relation contraire : pour toute formule de forme générale f(x) et une négation [N], la négation « contradictoire » est antéposée à la formule et s’écrit [N]f(x) tandis que la négation « contraire » est postposée à la formule et s’écrit f[N](x). Or Granger ne peut qu’être réticent à l’égard de cet isomorphisme, dans la mesure où il considère l’objet logique comme un objet absolument simple, c’est-à-dire sans structure. Nous reviendrons sur cette question de la structure de l’objet logique dans la prochaine section.

Un autre élément de la citation ci-dessus permet de mieux comprendre la distinction de Granger entre deux types fondamentaux de négation : la négation formelle est une fonction de vérité, ce qu’elle n’est pas le plus souvent dans le cas des oppositions aristotéliciennes : si la proposition « Tous les A sont B » est fausse, on ne peut effectivement pas déterminer la valeur de son contraire « Aucun A n’est B » puisque celle-ci peut alors être vraie ou fausse. Cela veut dire que la négation formelle s’applique à un objet quelconque dont la structure ne doit pas compter dans la détermination de sa signification. Granger (2001, p. 50) voit dans cette absence de structure une composante essentielle de la logique élémentaire :

N’entre ici que la dichotomie dite « de présence et d’absence » du point de vue des objets, « du vrai et du faux » du point de vue des actes de pensée.

À cette négation formelle « radicale », formatrice de contradictoire et typique de la logique « classique », Granger oppose les négations « particulières » dont le sens dépend d’une certaine structure. La logique des termes héritée d’Aristote est un exemple du genre, lorsque les expressions négatives s’appliquent aux termes de prédicats et produisent ce que les linguistes appellent des négations « affixes ». On peut trouver des exemples de formalisation de cette logique structurée dans plusieurs travaux[3], à rebours de la tradition logiciste de Frege limitée au discours mathématique. Granger reproche à chacune de ces négations « particulières » de dépendre d’un type de structure particulier : le modèle ou domaine dans lequel la négation s’applique, qu’il soit défini par une structure algébrique ou une structure d’ordre. On ne peut que rappeler ici l’influence du structuralisme mathématique de Bourbaki sur Granger, tout en insistant sur le fait que la notion de « structure » ne revêt pas chez le philosophe français le même sens dans ses trois différents contextes d’usage (linguistique, mathématique, et philosophique). Mais on doit insister tout à la fois sur l’opposition de Granger au pluralisme logique, bien que cette tendance à multiplier le nombre de systèmes logiques distincts trouve dans l’approche structuraliste un puissant allié théorique. Un exemple de structuration géométrique a été proposé à ce titre pour les négations multivalentes, basées sur des opérations de symétrie centrale (pour les négations booléennes et morganiennes) ou de rotation régulière (pour la négation cyclique)[4]. On peut mentionner le domaine non fini des nombres, avec la négation intuitionniste ; ou les sous-espaces linéaires de l’espace de Hilbert, avec la négation quantique. Granger (1988, p. 45) considère la négation par excellence comme la négation contradictoire, celle qui ne repose ni sur la structure du langage (les propositions) ni sur la structure du monde (le modèle d’interprétation du langage) :

On pourrait dire que, de même que les différentes théories de la modalité selon Kripke sont corrélatives de la structure des univers de « mondes possibles », et plus particulièrement de leur relation d’« accessibilité », de même les diverses théories propositionnelles dépendent de l’enrichissement en propriétés formelles de degré zéro de l’objet […]

Dans le cas de la négation paraconsistante, Granger (1988) se montre plus critique quant à sa légitimité : si celle-ci prétend admettre la coexistence de propositions contradictoires au sein d’un même ensemble de formules, alors un problème se pose quant au caractère contradictoire de leur relation. Granger (1988) met en doute cette coexistence ; il donne ci-dessous un exemple de syllogisme non contradictoire d’Aristote à partir duquel il va examiner des variantes supposées contradictoires :

L’homme est un animal.
Kallias est un homme.
Kallias est un animal.

Remplaçons les termes concrets ci-dessus par des lettres de variables : a pour « animal », b pour « homme », et c pour « Kallias ». On obtient alors un schéma logique consistant (α) duquel vont résulter deux types de schéma d’inconsistance (β1)-(β2) et dont Łukasiewicz attribue la paternité à Aristote :

(α)

(β1)

(β2)

b est a.

b est a (et n’est pas non-a à la fois).

b est a (et n’est pas non-a à la fois).

c est b.

c est bet n’est pasb.

c, qui n’est pasc, est b.

c est a.

c est a (et n’est pas non-a à la fois).

c est a (et n’est pas non-a à la fois).

Granger affirme qu’Aristote n’a jamais été un précurseur de la paraconsistance, dans la mesure où les cas d’inconsistance ci-dessus n’en sont pas réellement. Granger (1988, p. 43-44) cite Aristote[5] et l’explique ainsi :

Il s’agit apparemment pour Aristote de faire observer que, dans un syllogisme, les termes ont d’autres prédicats que celui dont il est question, et qu’ils sont par conséquent, à la fois, ceci et autre chose relativement à quoi ils ne sont évidemment pas ceci. Ce qui ne signifie nullement qu’on puisse admettre à la fois une proposition et sa propre négation contradictoire.

La « négation » ci-dessus n’est donc pas formatrice de contradiction, puisque le terme majeur « animal » serait sinon affirmé et nié à la fois du terme moyen « homme ». Notre position prolonge celle de Granger sur ce point, montrant qu’aucun cas de syllogisme dit « inconsistant » ne semble suffisant pour plaider en faveur de l’existence de « contradictions vraies ».

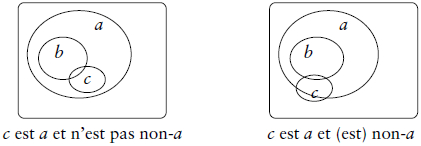
Dans un premier temps, Granger interprète la négation de la prémisse mineure soi-disant contradictoire de (β1) comme une expression de simple différence. Cela revient à considérer « Kallias n’est pas un homme » comme signifiant « Kallias n’est pas seulement un homme ». Cette négation n’étant pas exclusive, elle forme donc une relation non pas contradictoire mais subcontraire, c’est-à-dire une relation « partiellement inclusive » ou « partiellement disjointe » entre deux classes dans un modèle syllogistique. Mais si l’on admet cette interprétation affaiblie de la négation, la conclusion de (β1) n’est plus valide telle qu’elle apparaît dans sa forme strictement affirmative ci-dessus (voir Figure 1). Supposons en effet que Kallias ne soit pas un homme, comme le veut la prémisse mineure ; alors Kallias pourrait être une pierre dans une interprétation exclusive de la négation et, si tel était le cas, la conclusion serait fausse puisque Kallias est aussi un non-animal s’il est une pierre.

Figure 1

Deux modèles d’interprétation du syllogisme (β1).

-> See the list of figures

Dans un second temps, le second type de syllogisme (β2) semble bel et bien valide quant à lui en raison de la nature du terme qui y est affirmé et nié à la fois : « Kallias, qui n’est pas Kallias » figure comme terme sujet dans la prémisse mineure et est entièrement inclus dans le terme prédicat « homme ». L’inclusion totale du terme « homme » dans la classe des animaux implique ainsi l’inclusion totale du terme « Kallias » également, mais ce résultat n’est dû en rien à la signification de la négation. C’est cette fois-ci la structure d’ensemble, c’est-à-dire, la forme logique du syllogisme (β2) entier qui explique ce résultat ainsi que la différence entre les deux types de syllogismes « inconsistants » (β1) et (β2).

Un troisième type de syllogisme illustre mieux encore le problème de savoir si la négation est contradictoire ou ne l’est pas, dans la mesure où les exemples ci-dessus contiennent un terme singulier et ne comportent pas de quantificateurs caractéristiques des propositions catégoriques d’Aristote. L’exemple qui suit[6] est une version du mode Bocardo (de la troisième figure syllogistique) réduite à deux termes, en lieu et place des trois termes habituels :

forme: 2142509.jpg

L’explication précédente de Granger ne tient plus, ici : la négation paraît bel et bien contradictoire, dans la mesure où elle nie la prémisse majeure. Le critère de logicité de la consistance paraît contesté dans un tel cas de figure : deux prémisses contradictoires pourraient-elles être vraies ensemble ? Peu importe, en vérité, car la raison de la validité du syllogisme ci-dessus n’est pas d’ordre sémantique mais est purement syntaxique : c’est la forme logique qui permet d’en rendre compte dans le cas présent. Après avoir remplacé le terme majeur usuel c de la prémisse mineure par le terme majeur a de la prémisse majeure, la conclusion usuelle « Tout c n’est pas a » devient « Tout a n’est pas a » par simple application de la règle de substitution uniforme. La signification de la négation n’a donc rien à voir avec ce résultat contradictoire, de telle sorte que le critère de consistance n’est pas remis en cause en dépit des apparences : quiconque suppose la vérité de deux prémisses contradictoires en admettra la conclusion sans sourciller, aussi extravagante puisse-t-elle paraître ; mais quiconque connaît bien la syllogistique appliquera la règle des trois termes minimaux afin d’éviter ce cas de figure contradictoire.

Les exemples de syllogisme inconsistant chez Aristote n’en sont donc pas réellement, dans la mesure où l’occurrence de la négation n’y est pas essentielle et peut recevoir des interprétations variables : « tendancieuse » selon Granger, il est vrai que cette thèse d’une « contradiction vraie » a de quoi dérouter : qu’est-ce qu’un homme qui ne serait pas un homme à la fois, au sens exclusif de la négation, ou qu’est-ce qu’une classe qui s’exclurait elle-même ? La recherche de cette négation aurait été abandonnée par da Costa, selon Granger, faute d’interprétation possible au sein d’un modèle ; la hiérarchie des systèmes inconsistants[7] du même da Costa n’y changerait rien, si elle se réduit à un simple jeu de valuations arbitraires. C’est pourtant bien cette piste sémantique que nous allons poursuivre plus loin, afin de trouver une interprétation possible de ce que (Granger 1988, p. 43) appelle la « logique hégélienne » et qui s’accordera avec notre prochaine définition en compréhension de la négation.

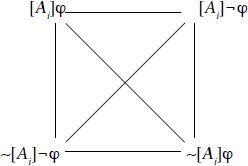
Revenons avant cela sur les relations d’opposition logique, exprimées par les énoncés catégoriques d’Aristote. Granger a raison de dire que la négation formatrice de contrariété (telle que la proposition qui en résulte ne peut pas être vraie si la première est vraie mais peut être fausse si la première est fausse) ne peut pas jouer le rôle d’une fonction de vérité appliquée à une proposition élémentaire dans un domaine bivalent : l’absence de structuration de la proposition élémentaire ne le permet pas, comparable à un point dans l’espace logique du Tractatus. C’est pour cette raison structurelle que, selon Granger, la négation fondamentale ne peut être autre que contradictoire (telle que la proposition qui en résulte ne peut pas être vraie si la première est vraie et ne peut pas être fausse si la première est fausse). En revanche, il devient possible d’admettre d’autres types de négation dès lors que la structure des propositions est complexifiée sur le modèle des fonctions. Et si la proposition était une entité complexe de type f(p), au lieu d’être réduite au statut de simple argument atomique p ? Dans ce cas de figure, la structure des propositions s’apparente à une fonction de type f(p) composée d’un quantificateur f = {tout, quelque} et d’une proposition affirmative p = ‘S est P’. La distinction reconnue par Granger entre contradiction et contrariété repose sur la structure ‘de degré un’ des propositions catégoriques, que l’on retrouve dans la logique de premier ordre et qui en dit plus sur le contenu des propositions que la simple logique propositionnelle « de degré zéro ». L’analogie structurelle qui suit entre propositions catégoriques et propositions affirmatives consiste à ajouter un opérateur d’affirmation au contenu propositionnel élémentaire. Cette morphologie plus complexe s’inscrit dans le carré de (Gottschalk 1953) et consiste à opposer deux types de fonctions unaires propositionnelles (voir Figure 2) : la négation d’une proposition p, « Ce n’est pas le cas que p » ou « La proposition p est fausse », d’une part ; l’affirmation d’une proposition p, « C’est le cas que p » ou « La proposition p est vraie », d’autre part.

Figure 2

Le carré de Gottschalk appliqué aux opérateurs de vérité T et de fausseté F de von Wright (1987).

-> See the list of figures

En appliquant le carré de Gottschalk au moyen de ces deux fonctions opposées, on obtient une logique des opérateurs de vérité T et de fausseté F, consacrée plus tard par von Wright (1987). Dans le diagramme consécutif, l’opérateur de vérité T se distingue de la valeur de vérité « Vrai » en ceci qu’il est une fonction, et non un objet. Comme l’a fait remarquer à juste titre un autre philosophe français, Robert Blanché, et corrigeant Piaget sur ce point dans Blanché (1966), le carré de Gottschalk n’est pas un carré aristotélicien, et ce pour au moins deux raisons. D’une part, la même fonction dite « contraduale » peut donner aussi bien une relation contraire (entre des formules qui ne peuvent pas être vraies ensemble) que subcontraire (entre des formules qui ne peuvent pas être fausses ensemble) : cela dépend de la structure de la proposition complexe à laquelle la négation s’applique. D’autre part, en quoi ce carré peut-il nous éclairer sur la valeur logique d’une formule quelconque ? Si p signifie « Il fait jour », alors quel est le type de relation logique entre les propositions « C’est le cas qu’il fait jour » et « C’est le cas qu’il ne fait pas jour » : contraire, si l’on admet leur vérité conjointe, ou subcontraire, si l’on si l’on considère cette compossibilité comme impossible ? N’en déplaise au premier Wittgenstein, une structure ne montre rien elle-même qui soit définitif et indépendant d’une explication préalable de ses règles de fonctionnement.

Dans la section à venir, nous allons clarifier certains points techniques présupposés dans l’étude ci-dessus de la négation et proposer une définition pluraliste basée sur la question du sens de la négation : une négation peut être formatrice de contradiction ou pas tout en respectant un seul et même schéma opératoire ; le nombre des formes de négations distinctes dépend de la complexité de la structure de l’objet logique à laquelle cet opérateur unaire s’applique, et notre position consistera à dire que cet objet fondamental n’est pas la proposition mais son « référent » frégéen : la valeur de vérité.

3. Fonction et objet

Qui dit « structure » dit « forme », et cette seconde notion tient une grande importance chez Granger. Plusieurs de ses travaux sont susceptibles d’intéresser le logicien et d’apporter de l’eau à notre moulin, que ce soit sous forme d’articles ou d’ouvrages plus aboutis. Nous ne citerons ici qu’une partie de ceux susceptibles de contribuer de près à la discussion qui va suivre : « Formes, opérations, objets » (1994) ; « L’irrationnel » (1998), « Science et réalité » (2001), ainsi que l’article « Contradiction » (1988). Ces textes sont assez récents et suivent d’autres réflexions plus générales sur la raison, le langage, ou la philosophie de Wittgenstein. Mais leur continuité est patente si l’on considère la question de la forme logique, essentielle du premier Wittgenstein jusqu’au thème de l’irrationnel en passant par la vérité scientifique.

L’importance de la notion de forme peut être formulée en termes très wittgensteiniens : si les limites de mon langage sont les limites de mon monde, quelles sont les formes qui délimitent ce langage, d’où viennent-elles, et à qui s’imposent-elles ? Les commentateurs de l’histoire de la logique contemporaine ont pour habitude de tracer sur ce thème clivant une ligne de démarcation entre deux façons de penser la logique : comme un langage universel, pour les universalistes ; comme un calcul, pour les algébristes. Cette distinction, associée au nom du logicien français Jean van Heijenoort, fait de la forme un socle absolu du langage logique, pour les premiers ; le résultat d’un processus opératoire entre les termes de ce langage, pour les seconds. Ce n’est pas le caractère abstrait des calculs algébriques ou de l’activité logique elle-même qui est remis en doute, pour ces derniers ; c’est plutôt le caractère universel de la logique et, partant, l’unicité des règles constitutives de la pensée logique, c’est-à-dire des limites de la rationalité en tant que telle. Notre problème général peut être reformulé ainsi : dans quelle mesure la logique est-elle universelle ? Le cas de Granger semble paradoxal à cet égard, puisqu’il défend tout comme les universalistes l’unicité de la logique tout en adoptant l’approche opératoire des algébristes.

Loin d’affirmer la moindre conclusion définitive sur ce sujet, nous allons nous consacrer au cas singulier de Granger en débutant par une question de méthode préalable : de quoi au juste la « forme logique » est-elle censée être la forme ? Puis en abordant ce problème fondamental par un autre problème plus particulier : celui de la signification logique de la négation, afin de nous inspirer des difficultés posées par sa définition et d’en tirer quelques enseignements sur la « stylistique logique » selon Granger.

S’agissant de son inspiration analytique évoquée au début de l’article, il convient de donner une place d’importance à Frege et à Wittgenstein. L’espace logique du dernier sera évoqué plus loin. Quant au premier, on ne peut ignorer l’influence d’au moins trois de ses travaux dans l’exposé qui suit : « Fonction et concept » (1891), « Concept et objet » (1892), « Sens et dénotation » (1892). D’une part, la distinction entre fonction et objet (ou argument) a permis non seulement d’aligner le processus de signification linguistique sur le modèle rigoureux de l’arithmétique, mais aussi d’augmenter le pouvoir explicatif de la logique par-delà les seuls prédicats monadiques de la syllogistique aristotélicienne. D’autre part, Frege a établi une distinction absolue entre fonction et objet : dans la proposition « Pégase est un cheval », la fonction unaire « est un cheval » est vraie de l’objet Pégase et de tout ce qui peut satisfaire la propriété chevaline. On doit aussi à Frege la distinction générale entre le sens d’une expression et son référent ; dans le cas des énoncés déclaratifs, ceux de la logique aristotélicienne, leur sens est une Proposition (au sens logique et non grammatical du terme) et leur référent est une valeur de vérité. Dans ce qui suit, nous allons nous appuyer sur cet héritage de Frege chez Granger pour tenter de mieux comprendre la philosophie de la logique de ce dernier. Non pas dans le cadre d’un travail d’histoire de la philosophie, mais dans une perspective critique et afin d’en extraire une logique philosophique à part entière. En commençant par une définition intensionnelle de l’opérateur de négation, puis en terminant par une explication unique de ses formes multiples.

Posons ainsi une thèse de départ, qui vaudra d’un bout à l’autre de l’exposé : la négation logique est une fonction (un foncteur, ou un opérateur) unaire qui s’applique à une valeur d’entrée x et qui consiste à exclure cette même valeur. Précisons que cette application ne correspond pas encore à l’opération d’involution, que Granger et l’usage commun associent à la négation « classique ». Si l’on prend l’exemple x = V où la valeur d’entrée x est la vérité, alors non seulement la transformation de la vérité en non-vérité n’implique pas encore la transformation converse de la non-vérité en vérité ; mais de plus, rien n’indique non plus que la non-vérité signifie la fausseté. La propriété d’« exclusion » fait que cette définition de la négation est intensionnelle, et non extensionnelle : l’opération qui la caractérise, tout en étant applicable à n’importe quelle valeur x par-delà le vrai et le faux, ne s’applique pas à n’importe quelle valeur d’entrée. La nature de l’objet x reste donc à expliquer, afin de bien saisir le sens et la portée de la définition ci-dessus.

Une telle définition ne semble pas poser de problème, si l’on en juge par la table de vérité de la négation « classique » ou « bivalente » [Nb] où x = T et son complément x̅ = F :

forme: 2142443.jpg

Mais un simple cas de figure de la logique multivalente suffit à produire un contre-exemple apparent. Soit @∈{N,B} une valeur tierce parmi deux possibles, telle que N = « ni vrai ni faux » ou B = « vrai et faux ». On constate alors les valuations suivantes dans la plupart des tables de vérité des négations trivalentes [Nt][8] :

forme: 2142444.jpg

La table de vérité ci-dessus ne semble déjà plus respecter notre définition générale, puisque la négation de la valeur @ laisse celle-ci inchangée. Pire encore : cet opérateur unaire laisse une proposition vraie inchangée lorsque @ = B, de sorte qu’une proposition et sa « négation » seront considérées comme vraies toutes les deux dans ce cas de figure. Cette situation d’inconsistance mentionnée dans la section précédente a conduit notamment à la fameuse critique de Slater (1995), dans un court article adressé en particulier à la logique paraconsistante « dialethéiste » de Priest (1979)[9]. Si la logique paraconsistante a survécu aux fourches caudines de Slater, son article a eu en tout cas le grand mérite de questionner la signification de la paraconsistance, et en particulier sa négation. Nous verrons plus loin la raison pour laquelle cette négation peut être qualifiée de « paraconsistante » (parce qu’elle enfreint le Principe d’explosion), et dans quelle mesure elle s’accorde avec notre définition de la négation (parce que l’opérateur de négation ne dépend pas du Principe de bivalence). Mais voyons d’abord si notre définition de la négation s’accorde avec l’histoire de cet opérateur logique.

4. Typologie des négations

Il existe un grand nombre de négations, si l’on en juge par la liste dressée dans la Stanford Encyclopedia of Philosophy. Négation classique, polaire (de contrariété), métalinguistique ; considérée comme une fonction de vérité, ou comme un opérateur modal. Associée à l’acte de rejet, ou à l’affirmation de fausseté. D’autres caractérisations existent, parmi les systèmes logiques homologués : négation intuitionniste, paraconsistante, linéaire, ontique, épistémique, quantique, booléenne, morganienne, externe, interne, cyclique, de terme, propositionnelle, logique, linguistique, etc. La liste ne saurait être exhaustive, faute de critère distinctif, et les membres de cette liste ne sont pas non plus exclusifs les uns des autres.

De façon générale, les diverses négations se distinguent les unes des autres par rapport à un ensemble de formules associées au système de référence de la logique classique. Bien que cette dernière soit assimilée au Principe de bivalence, un partisan de l’inférentialisme pourrait reprocher à cette assimilation de baser toute logique sur un critère sémantique du nombre de valeurs de vérité et d’admettre n’importe quel domaine de valuation sans restriction.

Nous allons défendre une position plus nuancée : la logique classique n’est pas basée sur le Principe de bivalence, tout en admettant un unique domaine de valuation initial composé de deux éléments minimaux : le vrai, et le faux. Cela est dû à une distinction entre bivalence et bivaluation, mais il est encore trop tôt pour en parler ici. Pour le moment, considérons un système logique quelconque L composé d’un langage formel et d’une relation de conséquence. Ce langage contient un ensemble de formules, des constantes logiques appliquées à ces formules, un domaine de valuation Vx composé de x valeurs de vérité, et un sous-ensemble de formules qui sont des théorèmes ou des tautologies (des formules vraies pour toute interprétation de ses sous-formules). Considérés dans ces termes, nous dirons que deux systèmes logiques L1 et L2 sont identiques si, et seulement si, ils contiennent le même sous-ensemble de théorèmes ou de tautologies.

À partir d’une lecture déflationniste du langage formel, on peut interpréter les propriétés suivantes de la négation « classique » en termes d’affirmations et de négations de contenus propositionnels. Ainsi, les expressions ‘φ’ et ‘¬φ’ signifient ‘(la proposition φ) est vraie’ et ‘(la proposition) φ est fausse’, respectivement. Quant à la double négation ‘¬¬φ’, nous l’interpréterons comme ‘(la proposition) φ n’est pas fausse’. Il résulte de ce langage formel un ensemble de formules caractéristiques de la négation « classique » :

Principe de non-contradiction (PNC)
⊨ ¬(φ ∧ ¬φ)
Aucune proposition n’est vraie et fausse à la fois.

Principe du tiers exclu (PTE)
⊨ φ ∨ ¬φ
Toute proposition est vraie ou fausse.

Lois de double négation (LDN)
(LDN1) ⊨ φ → ¬¬φ
Si une proposition est vraie, alors elle n’est pas fausse.
(LDN2) ⊨ ¬¬φ → φ
Si une proposition n’est pas fausse, alors elle est vraie.

Lois de De Morgan (LDM)
(LDM1) ⊨ ¬(φ ∧ ψ) → (¬φ ∨ ¬ψ)
Si la conjonction de deux propositions est fausse, alors au moins une des deux est fausse.
(LDM2) ⊨ (¬φ ∨ ¬ψ) → ¬(φ ∧ ψ)
Si au moins une parmi deux propositions est fausse, alors la conjonction des deux propositions est fausse.
(LDM3) ⊨ ¬(φ ∨ ψ) → (¬φ ∧ ¬ψ)
Si la disjonction de deux propositions est fausse, alors les deux propositions sont fausses.
(LDM4) ⊨ (¬φ ∧ ¬ψ) → ¬(φ ∨ ψ)
Si deux propositions sont fausses, alors la disjonction des deux propositions est fausse.

Loi de contraposition (LC)
⊨ (φ → ψ) → (¬ψ → ¬φ)
Si la vérité d’une proposition implique la vérité d’une autre, alors la fausseté de la seconde implique la fausseté de la première.

Loi d’explosion (LE)
⊨ (φ ∧ ¬φ) → ψ
La vérité et la fausseté d’une proposition impliquent la vérité de toute autre proposition.

Syllogisme disjonctif (SD)
⊨ ((φ ∨ ψ) ∧ ¬φ) → ψ
Si une proposition d’une disjonction vraie est fausse, alors l’autre proposition est vraie.

Deux problèmes apparaissent ici. Le premier concerne le choix d’interprétation déflationniste de la négation propositionnelle en termes d’affirmation de fausseté : n’y a-t-il aucune différence logique entre l’affirmation d’une fausseté et la négation d’une vérité ? Le second concerne le risque de définition circulaire de la négation : comment la définir correctement par le biais d’autres constantes telles que la conjonction, la disjonction et le conditionnel, sachant que celles-ci utilisent également la négation pour être expliquées ?

Répondre à ces questions exige une étude plus approfondie de l’objet sur lequel porte la négation logique : la valeur de vérité.

5. L’objet logique

La position de Granger sur la nature de l’« objet logique » paraît ambiguë au premier abord. Dans un article dédié à ce concept, Granger (2005, p. 205) affirme d’abord et à la façon d’un Wittgenstein qu’« il n’y a pas d’objet logique », au sens où les seuls objets proprement dits sont les entités constitutives des états de choses du monde. Puis il semble dire le contraire en affirmant qu’il existe un objet logique et que cet objet est la proposition :

L’objet logique au sens le plus strict est la proposition, élément symbolique significatif ultime d’un langage.

Cet objet n’est donc pas l’objet exprimé par la proposition ou son référent, mais la proposition elle-même. On peut expliquer ce revirement apparent du Granger-commentateur de Wittgenstein par sa conception opératoire de la logique. En ce sens, Granger est bien plus proche d’un Piaget ou d’un Łukasiewicz que d’un Wittgenstein ou d’un Frege. Proche de Piaget (1949, p. 5), lorsque celui-ci dit d’une part que la logique est une « théorie des opérations sur l’objet en général », que cet objet soit une proposition ou tout autre élément constitutif d’un système d’opérations. Proche de Łukasiewicz, lorsque celui-ci décrit dans Łukasiewicz (1970, p. 90) la logique comme théorie des valeurs de vérité en termes bivalents :

Les objets dénotés par des propositions sont appelés des valeurs logiques. La vérité est la valeur logique positive, et la fausseté est la valeur logique négative. La logique est la science d’objets d’un type particulier, à savoir, une science des valeurs logiques.

Que l’on se rappelle le lien fondamental entre ces valeurs de vérité et leurs « porteurs » que sont les propositions, et l’on comprendra mieux la parenté entre Granger et Łukasiewicz. Mais la comparaison entre les deux philosophes de la logique a ses limites. Car Granger ne pense pas la logique en d’autres termes que bivalents, si l’on entend par là la restriction des valeurs de vérité au nombre de deux. La différence est grande, dans ce cas, entre Granger et le grand contributeur de la multivalence que fut Łukasiewicz. Comment expliquer ce différend, d’autant plus que la citation précédente du logicien polonais évoquait les termes binaires d’être et de non-être ? Granger (1994, p. 43) tient un propos similaire :

Le calcul propositionnel se développe en effet comme prolifération indéfinie, mais parfaitement maîtrisée par la pensée, des variations sur le thème nucléaire de la partition de l’univers entre le posé et le non-posé : p, ou non-p.

D’apparence très bivalente, une telle affirmation n’est en fait pas incompatible avec la multivalence de Łukasiewicz. Elle ne l’est pas, du moins, si l’on définit les valeurs de vérité « non classiques » comme une combinaison des deux valeurs fondamentales que sont le vrai et le faux, plutôt que comme des valeurs définies par d’autres éléments que le vrai et le faux. Si la position de Granger paraît si « classique » en la matière, c’est sans doute parce que la logique classique n’admet que deux valeurs de vérité et que chacune d’elles y est considérée comme le référent unique d’une proposition. Suszko (1977) a reproché à cet « axiome de Frege » de reposer sur une définition arbitraire du référent de la proposition : selon lui, ce référent devrait être un fait plutôt qu’une valeur de vérité. Il n’a pas contesté en revanche le second volet de cet axiome, en vertu duquel toute proposition ne pourrait avoir que deux référents parmi le Vrai et le Faux. Son rejet des logiques multivalentes repose sur une distinction entre deux types de valeurs : les valeurs logiques, qui sont les deux éléments fondamentaux de la vérité et de la fausseté ; les valeurs algébriques, qui sont des ensembles ordonnés incluant les deux éléments précédents (vrai, faux) ou leurs complémentaires (non-vrai, non-faux). Deux exemples de valeurs « algébriques » sont les valeurs dites « lacunaires » (ni vrai et ni faux) et « excédentaires » (vrai et faux). Notre position sera exactement contraire à celle de Suszko par rapport à l’axiome de Frege : oui, le référent d’une proposition est une valeur de vérité ; et non, ce référent n’est pas restreint aux deux valeurs du simplement vrai et du simplement faux. À la question : combien de valeurs de vérité peut-il y avoir au-delà du vrai et du faux, nous répondrons : un nombre indéfini, mais toujours sur la base d’une partition d’une seule et unique valeur fondamentale : le Vrai, dont le Faux est aussi un produit dérivé.

Voyons donc de plus près ce qu’est une valeur de vérité, l’objet auquel nous disons ici que la négation s’applique ; et surtout, voyons dans quelle mesure la structure de cet objet particulier justifie la thèse de Granger sur le degré de complexité de l’objet logique en général.

Qu’est-ce qu’une valeur de vérité ? Plusieurs tentatives de réponses, non exclusives les unes des autres, sont exposées dans l’article du Stanford Encyclopedia of Philosophy qui lui est consacré :

  1. des objets abstraits primitifs dénotés par des énoncés au sein de langages naturels et formels ;

  2. des entités abstraites hypostasiées, à valeur de classes d’équivalence d’énoncés ;

  3. ce qui est visé dans un jugement ;

  4. des valeurs indiquant le degré de vérité d’énoncés ;

  5. des entités qui peuvent être utilisées pour expliquer le caractère vague de concepts ;

  6. des valeurs qui sont préservées dans des inférences valides ;

  7. des valeurs qui transmettent une information à propos d’une proposition donnée.

Notre plaidoyer pour des valeurs structurées consiste à admettre les propriétés (a), (b), (c), (f) et (g), à rejeter (d), et à laisser le cas de (e) en suspens[10]. La position de Granger sur la question semble de nouveau conforme à celle d’un Quine, fermement opposé à l’idée de valeurs autres que le vrai et le faux. Elle confirme aussi et surtout l’idée que, pour Granger (2001, p. 92), la valeur de vérité est un objet absolument simple et donc sans structure ou « amorphe », lorsque celui-ci parle de la logique comme d’une théorie comprenant deux objets « sans qualités », le vrai et le faux, et l’ensemble des opérations de déduction autorisées dans le système.

Le même point de vue semble apparaître chez Łukasiewicz (1970, p. 90), ce qui peut surprendre de la part de ce partisan de la multivalence :

Toutes les propositions vraies dénotent un seul et même objet, la vérité, et toutes les propositions fausses dénotent un seul et même objet, la fausseté. Je considère la vérité et la fausseté comme des objets singuliers, au même sens que le nombre 2 ou le nombre 4.

Pourquoi deux, et seulement deux valeurs ? Les logiciens diront que cette partition est le tarif minimal pour donner sens à la relation de conséquence sémantique ; car si toutes les propositions étaient vraies ou fausses à la fois, alors notre langage serait trivial puisque tout se vaudrait sans distinction. Des philosophes ajouteront qu’il n’y a rien en dehors de l’être et du non-être, et que rien n’échappe à cette dualité. Pas même les valeurs de vérité, fussent-elles algébriques ? La philosophie de la logique de Granger apparaît comme une combinaison de ces deux points de vue. Par opposition, notre position sera différente de celle exprimée par Łukasiewicz (1970, p. 90) en ceci qu’elle ne partage pas sa lecture « ontologique » des valeurs de vérité :

Ontologiquement, la vérité a son analogue dans l’être, et la fausseté dans le non-être.

Tout au contraire, il s’agit de montrer l’utilité explicative des valeurs algébriques par le biais de leurs structures. Une autre lecture des valeurs de vérité, de type épistémologique, ne considère pas les propositions comme des expressions de faits ou états de choses mais comme des informations ou situations. Elle repose sur le modèle des réseaux d’ordinateurs proposé par Belnap (1977), dans lequel les valeurs de vérité ne sont pas des valeurs intrinsèques aux propositions mais de simples marqueurs de jugements provisoires exprimés par des énoncés. Un énoncé n’est donc pas vrai ou faux au sens absolu du terme : il est « considéré comme » tel, jusqu’à preuve du contraire. Là est sa marque de fabrique épistémique. Si un énoncé est considéré comme vrai, cela veut dire qu’il existe une information susceptible de le confirmer et aucune pour l’infirmer. S’il existe une information susceptible de le confirmer et une autre susceptible de l’infirmer, il sera considéré comme vrai-et-faux. Et ainsi de suite, proportionnellement au nombre de combinaisons d’informations distinctes[11].

De même qu’il peut y avoir autant de paires de chaussettes distinctes que de couleurs distinctes et composées à partir des quatre couleurs primaires, il peut y avoir autant de valeurs de vérité que de valeurs distinctes et composées à partir d’une valeur fondamentale qui s’appelle le Vrai.

V1 = {T} = {1}
(1 valeur : vrai)

V2 = {{T},{forme: 2142445.jpg}} = {T, F} = {1,0}
(2 valeurs : vrai, non-vrai = faux)

forme: 2142446.jpg
(4 valeurs : vrai et non-vrai = vrai-et-faux, vrai et non non-vrai = vrai et non-faux = vrai, non-vrai et faux = faux, non-vrai-et-non-faux)
…

Le domaine quadrivalent V4 est déjà plus compréhensible lorsqu’il est expliqué en termes de données en réseaux, et le même processus peut être appliqué à des domaines toujours plus complexes tels que V16. Si une ‘contradiction’ peut être admise dans V4, dans la mesure où un énoncé peut y être considéré comme vrai-et-faux, alors une hyper-contradiction[12] peut apparaître dans V16 dans la mesure où un énoncé peut y être considéré comme vrai-et-faux et non(vrai-et-faux) à la fois. La signification de cette valeur dépend de la structure du réseau d’informations, ainsi que des liens qui existent entre chaque source d’information. On peut comparer un tel modèle à un ensemble de mondes possibles sans relation d’accessibilité réciproque, toute proportion gardée sur l’analogie entre notre sémantique algébrique et la sémantique relationnelle de Kripke. Son processus de formation est quoiqu’il en soit le suivant : chaque domaine de valeur Vn inclut m éléments xi, xj, …, et le nombre 2m = n des valeurs de vérité structurées d’un domaine correspond au nombre des parties ou sous-ensembles de ce domaine. Ainsi le premier domaine V1 ne constitue-t-il pas un domaine de valeurs complet, au sens où il y manque l’ensemble vide comme partie de cet ensemble-singleton. Le domaine binaire V2 est le domaine de valeurs primordial, ce domaine se composant du Vrai T et d’un ensemble vide : le Faux F, c’est-à-dire la valeur négative forme: 2142447.jpg. L’accroissement successif des domaines implique que l’ensemble vide de chaque ensemble comprenant m éléments devient lui-même un sous-ensemble non vide dans le domaine suivant qui comprend 2m éléments : ainsi, le Faux F n’existe pas plus dans V1 que le Ni-Vrai-Ni-Faux N n’existe dans V2, que le Vrai-et-Faux-et-Vrai-et-non-Faux BT n’existe dans V4, etc.

En quoi cette théorie des valeurs de vérité structurées peut-elle éclairer notre problème initial des formes de la négation ? En ceci qu’elle permet de voir sous un autre éclairage un principe situé à mi-chemin entre la négation et les valeurs de vérité : le Principe de bivalence (PBV). Le sens commun et Granger associent ce principe à la logique classique, au sens où les conditions de vérité des constantes logiques classiques permettent de valider toutes les formules logiques citées précédemment et associées à la logique classique. (PBV) nous dit que toute proposition est soit vraie soit fausse, exclusivement et exhaustivement. Ce principe résulte de la combinaison des quatre conditions (PBV1)-(PBV4) qui suivent, où la précaution est prise de ne pas identifier l’absence d’un élément xi quelconque avec la présence automatique d’un autre élément xj.

  • (PBV1) Si φ est vraie, alors φ n’est pas fausse.

  • (PBV2) Si φ est fausse, alors φ n’est pas vraie.

  • (PBV3) Si φ n’est pas vraie, alors φ est fausse.

  • (PBV4) Si φ n’est pas fausse, alors φ est vraie.

Revenons à l’analogie structurelle (mentionnée dans la section 2) entre les propositions catégoriques d’Aristote et les propositions affirmatives et négatives de von Wright : de même qu’il existe des opérateurs de négation bien établis dans la tradition logique, (PBV) peut être considéré comme un produit d’opérateurs d’affirmation, les deux types d’opérateurs unaires affirmatifs et négatifs se comportant comme des opérateurs partiels de forme générale [Oi][13]. Le comportement « partiel » de ces opérateurs est dû au fait qu’ils ne transforment que certaines valeurs d’entrée en d’autres valeurs de sortie. En vertu de cette définition des opérateurs unaires d’affirmation et de négation, l’argument x sur lequel ils portent est une valeur algébrique constitutive d’une valeur logique. Autrement dit, si x correspond à la valeur algébrique Vrai ou Faux alors sa négation x correspond à la valeur algébrique Non-Vrai ou Non-Faux. Il est important de comprendre que cette valeur négative x n’est pas le simple complémentaire de x mais constitue le résultat d’un opérateur formateur de valeur unique, bien que structurellement complexe. Cette valeur est donc « singulière », en accord avec le propos de Łukasiewicz ; mais elle n’est pas simple, par opposition à la valeur de vérité de Frege.

En sus de la négation logique, l’affirmation logique est un opérateur unaire qui s’applique à une valeur xi d’entrée quelconque et consiste à exclure une autre valeur xj. Pour être plus précis, l’affirmation [A] est un opérateur unaire appliqué à un objet x qui est la référence d’une formule j et tel que, pour tout domaine Vx :

forme: 2142448.jpg

Les quatre opérateurs partiels d’affirmation [Ai] qui caractérisent (PBV) peuvent être définis comme suit, parallèlement à chacune de ses propriétés (PB1)-(PB4) : pour toute formule φ,

forme: 2142449.jpg

Les deux premiers opérateurs [A1]-[A2] imposent la condition d’exclusivité de (PBV) dans un domaine ; les deux derniers, [A3]-[A4], la condition d’exhaustivité. La complexité du concept de bivalence et, plus loin, celle des différents types de négation logique, va être expliquée dans ce qui suit au moyen d’un opérateur algébrique de produit, ⊗[14].

Dire que (PBV) constitue un produit de ces fonctions, c’est dire que ce principe résulte de la combinaison des quatre opérateurs d’affirmation [A1]-[A4] :

forme: 2142450.jpg

Le même processus d’application partielle vaut pour la négation [N], sur la base de la définition fondamentale que nous en avons donnée au début de cet article :

forme: 2142451.jpg

Alors qu’il est redondant dans une sémantique « classique » à deux valeurs de vérité, l’opérateur d’affirmation [Ai] devient significatif dans un domaine enrichi et permet même d’expliquer les divergences d’interprétation entre plusieurs types de système logique. Mieux encore, la distinction entre affirmation et négation permet de voir, au sens formel du terme, que ces divergences ne reposent pas sur la négation mais sur l’affirmation, telle que nous l’avons définie ci-dessus et qui détermine les conditions dans lesquelles une proposition peut être considérée comme vraie, fausse, les deux, ou ni l’une ni l’autre.

Revenons à la négation. Par-delà la typologie pléthorique des négations de Granger (1988), qui ne nous aide en rien à y voir plus clair sur le critère de la négation logique, notre définition constructive ci-dessus donne lieu à un total de 24 - 1 = 15 opérateurs sur la base de l’ensemble des m = 4 valeurs élémentaires {T,F,forme: 2142452.jpg,forme: 2142453.jpg} et dont la complexité varie en fonction du nombre de produits effectués entre ces opérateurs :

forme: 2142454.jpg

Nous pouvons identifier un type de négation récurrent au sein de l’ensemble ci-dessus : la négation booléenne [N15] ; l’autre type de négation important dans la plupart des systèmes logiques, la négation morganienne, n’y figure pas. L’une et l’autre sont à la négation ce que la nécessité et la possibilité sont à la logique modale : la stricte possibilité exclut la nécessité, de même que la négation strictement morganienne exclut la propriété booléenne d’involution (en vertu de laquelle la double négation équivaut à l’affirmation).

On peut construire ainsi la négation booléenne comme un produit maximal de négations partielles [Ni] :

forme: 2142455.jpg

Sa table de vérité caractéristique est telle que les symboles 1 et 0 sont ordonnés dans le domaine quadrivalent V4 pour former les quatre valeurs algébriques B = 11, T = 10, F = 01, et N = 00.

forme: 2142456.jpg

La négation morganienne est plus complexe, irréductible à un simple produit de négations partielles. Pour en expliquer le mode de construction, allons plus loin dans le processus calculatoire et distinguons deux types de fonctions unaires :

  1. les opérateurs simples, qui comprennent l’affirmation simple [Ai] et la négation simple [Ni].

  2. la fusion de deux opérateurs simples identiques, comme c’est le cas dans la négation affirmée [ANi] et l’affirmation niée [NAi],

    forme: 2142457.jpg

    ou de deux opérateurs distincts, comme dans l’affirmation affirmée [AAi] et la négation niée [NNi],

    forme: 2142458.jpg

[NN] et [AA] incarnent la propriété d’involution associée couramment à la négation « classique », dans la mesure où la double application du même opérateur partiel reproduit la valeur d’entrée. On peut montrer ce processus opératoire comme suit :

forme: 2142459.jpg

Il est important de préciser également que ces fusions d’opérateurs [OOi](x) sont différentes des itérations d’opérateurs : [Oi][Oj](x), une simple preuve par induction sur des tables de vérité montrant que [OOi](x) ≠ [Oi][Oi](x).

On peut construire dès lors la négation morganienne comme le produit maximal de négations affirmées (ou d’affirmations niées). Ainsi :

forme: 2142460.jpg

Deux remarques générales, à propos des opérateurs partiels [Ox]. D’abord, les opérateurs fusionnés ne sont pas nécessairement involutifs : ce sont des négations mixtes qui, telle la négation morganienne, peuvent laisser une proposition vraie inchangée ; mais cette négation n’est pas uniquement formatrice de contradictions, comme le montrent la table de vérité ci-dessus et le cas précédent de la table de vérité trivalente (voir section 3, page 9). Ensuite, la diversité des opérateurs d’affirmation et de négation exige une amélioration de leur forme logique. Mais pour ce faire, encore faut-il rejeter l’interprétation déflationniste des formules et trouver une forme capable de faire la distinction entre l’affirmation d’une fausseté et la négation d’une vérité. Sans cette précaution d’usage, il est en effet impossible de traduire différents systèmes logiques au sein d’un seul et même langage formel.

Par analogie avec le cas précédent de la négation, on peut construire un total de 24 - 1 = 15 types d’opérateurs d’affirmation quadrivalents [A1]-[A15]. En voici la liste complète :

forme: 2142461.jpg

Parmi cette liste exhaustive des opérateurs d’affirmation partiels [Ax], trois méritent une attention particulière : [A5], [A8], et [A10]. Nous pouvons voir dans ces opérateurs respectifs une traduction logique des « systèmes philosophiques » que sont l’intuitionnisme (ou scepticisme), le réalisme, et l’éclectisme. Leurs tables de vérité caractéristiques sont les suivantes :

forme: 2142462.jpg

Non seulement ces opérateurs d’affirmation permettent de valider tout ou partie des formules caractéristiques de la logique « classique » : [A5] restreint le domaine quadrivalent de départ V4 à un domaine intuitionniste à trois valeurs (de type Kleene 1938) VK3 = {10,01,00} ; [A8] à un domaine classique à deux valeurs V2 = {10,01} ; et [A10] à un domaine paraconsistant à trois valeurs (de type Priest 1979) VP3 = {11,10,01}. Mais de plus, ils montrent que ces différents systèmes ne se distinguent pas par leurs négations. Ce sont les deux mêmes types de négation : la négation booléenne [N15] et la négation morganienne [AN15], qui apparaissent dans les trois cas de figure mais se combinent à des types d’opérateurs d’affirmation [Ai] distincts.

Maintenant que l’objet logique et la structure de cet objet ont été mis à jour, il nous est permis d’exposer une version du pluralisme logique qui satisfasse les critères techniques de la logique selon Granger sans maintenir son présupposé philosophique de la bivalence.

6. Pluralisme et valeurs de vérité

Nous avons cité au début de l’article plusieurs penseurs essentiels dans le champ de la logique et de l’épistémologie française du xxe siècle, parmi lesquels Martial Gueroult et Jules Vuillemin. Ce n’est pas un hasard si Granger a partagé avec eux le souci de bien définir le concept de vérité et, notamment, de répondre à la question de savoir s’il existe plusieurs sortes de vérité dans ce que Vuillemin appelait les « systèmes philosophiques ». (Feghally 2016, p. 205) insiste dans la conclusion de sa réflexion sur deux points : bien que Granger fût en désaccord avec Gueroult et Vuillemin quant à la possibilité d’axiomatiser ces « systèmes », tous trois s’accordaient sur le caractère irréductiblement pluriel de la définition du concept de vérité en leur sein :

La tradition veut que l’on associe systématicité et absolutisme d’un côté, pluralisme et relativisme de l’autre. Vus sous cet angle, Gueroult, Vuillemin et Granger seraient les philosophes les moins traditionnels. Et la raison de cela n’est pas difficile à comprendre : en plus de leurs pensées systématiques, tous les trois posent le pluralisme comme une condition constitutive de la philosophie ; tous les trois refusent de voir dans le pluralisme l’équivalent du relatif ou de l’arbitraire ; enfin, tous les trois soutiennent que la systématicité n’implique pas la recherche d’un système absolu qui serait le vrai.

La contribution centrale que cet article veut apporter à la philosophie de Granger est la suivante : trouver un langage formel dans lequel la pluralité des formes logiques révèlerait la pluralité de ces « systèmes philosophiques ». Or si cette tâche exige une analyse plus profonde de la façon dont des agents peuvent être en désaccord mutuel sur les conditions de vérité d’un même énoncé, alors elle exige notamment (mais pas seulement) une analyse plus profonde du concept de négation.

Pour dresser une analyse comparative de ces différentes formes de négation, nous avons besoin d’un langage formel commun dans lequel la traduction des divers types de négation logique conduit à des formulations univoques distinctes. Tous les locuteurs de ce langage commun partagent un seul et même usage des actes d’affirmation et de négation. Ainsi, l’acte d’affirmation consiste à exprimer ce que le locuteur est en droit de considérer comme une vérité, conformément à ses propres critères de justification. La traduction commune de l’acte de négation est plus délicate puisque, comme nous l’avons expliqué plus haut, il s’agit de faire la part des choses entre la négation comme attitude catégorique d’affirmation de fausseté ou réfutation, d’une part, et la négation comme attitude plus modérée de simple récusation ou rejet, d’autre part. Il résulte de ce travail d’analyse logique des formes opératoires plus complexes qu’à l’accoutumée, dans lesquelles la signification du contenu propositionnel dépend des critères épistémiques du locuteur et figure donc toujours dans la portée d’un opérateur d’affirmation préalable :

Affirmation
Pour tout φ, l’affirmation de φ est de forme [Ai]φ.

L’acte de négation entendu comme réfutation ne s’applique pas directement au contenu propositionnel, mais à l’affirmation préalable de celui-ci : dire d’un énoncé qu’il est faux, c’est affirmer qu’il n’est pas vrai en vertu des critères de justification du locuteur. Cet acte correspond à la négation morganienne et nous la qualifierons également de négation forte, aussi bien en raison de sa parenté avec la négation de Nelson (1949) que de sa signification linguistique.

Négation forte
Pour tout φ, la réfutation de φ est de forme [NA15][Ai]φ.

Les cas de la double négation et de l’itération en règle générale trouvent une explication précise au sein de ce langage formel commun : la négation appliquée à l’affirmation est une négation morganienne ou « forte », tandis que la négation appliquée à cette négation forte est une négation booléenne que l’on peut qualifier de « faible » par opposition à son homologue morganienne.

Négation faible
Pour tout φ, le rejet de φ est de forme [N15][Ai]φ.

Le pluralisme logique provient dès lors des différentes façons d’affirmer ou de nier un contenu propositionnel en fonction du traitement de ses valeurs de vérité. En simplifiant le symbolisme logique des deux types de négation, tel que [AN15] = ¬ et [N15] = ~, on obtient la nouvelle traduction suivante des propriétés principales de la négation dite « classique ».

Principe de non-contradiction (PNC)
⊨ ~([Ai]φ ∧ ¬[Ai]φ)
Aucune proposition n’est vraie et fausse à la fois.

Principe du tiers exclu (PTE)
⊨ [Ai]φ ∨ ¬[Ai]φ
Toute proposition est vraie ou fausse.

Lois de double négation (LDN)
(LDN1) ⊨ [Ai]φ → ~¬[Ai]φ
Si une proposition est vraie, alors elle n’est pas fausse.
(LDN2) ⊨ ~¬[Ai]φ → [Ai]φ
Si une proposition n’est pas fausse, alors elle est vraie.

Lois de De Morgan (LDM)
(LDM1) ⊨ ~([Ai]φ ∧ [Ai]ψ) → (¬[Ai]φ ∨ ¬[Ai]ψ)
Si la conjonction de deux propositions n’est pas vraie, alors au moins une des deux est fausse.
(LDM2) ⊨ (¬[Ai]φ ∨ ¬[Ai]ψ) → ~([Ai]φ ⊗ [Ai]ψ)
Si au moins une parmi deux propositions est fausse, alors la conjonction des deux propositions n’est pas vraie.
(LDM3) ⊨ ~([Ai]φ ∨ [Ai]ψ) → (¬[Ai]φ ∧ ¬[Ai]ψ)
Si la disjonction de deux propositions n’est pas vraie, alors les deux propositions sont fausses.
(LDM4) ⊨ (¬[Ai]φ ∧ ¬[Ai]ψ) → ~([Ai]φ ∨ [Ai]ψ)
Si deux propositions sont fausses, alors la disjonction des deux propositions n’est pas vraie.

Loi de contraposition (LC)
⊨ ([Ai]φ → [Ai]ψ) → (¬[Ai]ψ → ¬[Ai]φ)
Si la vérité d’une proposition implique la vérité d’une autre, alors la fausseté de la seconde implique la fausseté de la première.

Loi d’explosion (LE)
⊨ ([Ai]φ ∧ ¬[Ai]φ) → [Ai]ψ
La vérité et la fausseté d’une proposition impliquent la vérité de toute autre proposition.

Syllogisme disjonctif (SD)
⊨ (([Ai]φ ∨ [Ai]ψ) ∧ ¬[Ai]φ) → [Ai]ψ
Si une proposition d’une disjonction vraie est fausse, alors l’autre proposition est vraie.

La pluralité des points de vue sur les conditions de vérité des énoncés ne réside pas ici dans un désaccord relatif à la signification des autres constantes logiques que sont la disjonction ∨, la conjonction ∧ et le conditionnel →, puisque toutes sont définies de la même façon pour tous les types de locuteurs. Ainsi :

Conjonction
(φ ∧ ψ) est vrai si et seulement si φ est vrai et ψ est vrai.

Disjonction
(φ ∨ ψ) est vrai si et seulement si φ est vrai ou ψ est vrai.

Conditionnel
(φ → ψ) est vrai si et seulement si φ n’est pas vrai ou ψ est vrai.

Considérant la relation de conséquence logique comme préservation du vrai des prémisses aux conséquences, le tableau qui suit montre que la validité des propriétés de la négation « classique » dépend essentiellement du comportement de [Ai].

forme: 2142463.jpg

Notre langage formel commun a l’avantage de prolonger la position pluraliste de Granger, relevée dans Feghaly (2016, p. 205-206) :

La condition plurielle de la connaissance philosophique, ce n’est pas, comme le dit Granger, l’indice d’un relativisme, d’un scepticisme ou d’un éclectisme.

Dans ce langage formel, le pluralisme est une propriété métalogique caractérisée par la diversité des opérateurs partiels [Ai], tandis que le scepticisme et l’éclectisme sont des opérateurs particuliers du langage-objet. C’est le cas également pour le relativisme, même s’il n’est pas exprimé dans le tableau ci-dessus[15].

Pour conclure cette section, nous noterons que l’opérateur d’affirmation paraconsistante [A10] permet de répondre à un problème posé précédemment (voir note 8) et relatif à la structure du carré des oppositions affirmatives (voir Figure 3) : s’il est effectivement possible d’affirmer à la fois « C’est le cas qu’il fait jour » et « C’est le cas qu’il ne fait pas jour », c’est parce que le sens de son opérateur de vérité T est affaibli lorsqu’il est interprété au sens de l’affirmation paraconsistante [A10], tandis que la vérité « classique » doit être interprétée au sens de [A8]. Dans le premier cas de figure, Tφ et T¬φ ne sont pas contraires mais subcontraires à nouveau ; un logicien paraconsistant tel que Priest affirmerait tout aussi bien « C’est le cas qu’il fait jour et qu’il ne fait pas jour »,

T(φ ∧ ¬φ),

lorsque T = [A10]. On voit que T se comporte dans ce cas comme l’opérateur modal de possibilité[16], toute proportion gardée sur les rapports de traduction entre les modalités logiques et nos opérateurs partiels. Priest affirmerait-il tout aussi bien « C’est le cas qu’il fait jour et ce n’est pas le cas qu’il fait jour »,

Tφ ∧ ~Tφ ?

Son sens de la vérité ne le permettrait pas et, pour cette raison, sa défense des « contradictions vraies » repose sur une confusion entre les concepts de contradiction et de négation.

7. Conclusion : Un style logico-philosophique

Nous avons voulu montrer dans cet article que la négation logique de Granger repose sur deux critères essentiels : le degré de complexité de la structure de l’objet auquel cette fonction unaire s’applique ; le travail prépondérant du logicien-philosophe dans la constitution de cette structure.

Notre plaidoyer en faveur d’une valeur de vérité structurée conduit à un jugement nuancé sur deux aspects frégéens de la pensée logique de Granger : sur la simplicité de l’objet logique, d’une part ; sur la distinction absolue entre fonction et objet, d’autre part.

Figure 3

Le carré de Gottschalk appliqué aux opérateurs d’affirmation [Ai].

-> See the list of figures

Sur la simplicité des valeurs de vérité, notre avis ne peut être que négatif. Pourquoi Granger n’a-t-il pas admis une définition plus générale et pourquoi a-t-il maintenu, notamment, une différence de nature (au lieu d’une simple différence de degré, de complexité) entre négation logique et négation linguistique ? La raison tient au type de structure auquel Granger faisait allusion, dans son analyse de la négation : ce ne peut être à ses yeux que celle de la proposition, au sein d’un langage constitué de relations entre elles et d’opérations sur elles. La philosophie de la logique de Granger semble être frégéenne et ne pas l’être à la fois. Elle l’est, dans la mesure où elle souscrit comme Frege à la distinction absolue entre fonction et objet et à la simplicité de l’objet logique qu’est la valeur de vérité. Elle ne l’est pas, dans la mesure où elle insiste davantage sur le caractère opératoire de la logique et ne suppose pas d’emblée l’unicité de la relation sémantique entre le langage et le monde. C’est sans doute le postulat de simplicité de la valeur de vérité qui, chez lui, implique l’unicité de cette relation sémantique et fait du processus de partition de la pensée un garant de la bivalence. On peut distinguer quatre attitudes vis-à-vis de l’axiome de Frege, selon lequel le référent d’une proposition est une valeur de vérité qui est soit le Vrai soit le Faux : admettre ses deux volets, comme le fit Granger ; admettre le second volet mais pas le premier, comme le fit Suszko ; admettre le premier volet mais pas le second, ce qui fut notre cas ici ; n’admettre aucun des deux, ce qui est plus rare voire inédit.

Sur la distinction absolue entre fonction et objet, notre avis est positif mais réclame davantage qu’une simple distinction de principe. Certes, une fonction de vérité n’a pas le même statut ontologique qu’une valeur d’individu dans un langage formel, et nous serons même enclins à admettre qu’elle n’en a aucun. Mais si la négation n’est pas un objet, pourquoi doit-on en dire autant des autres types de fonctions tels que les prédicats unaires : « cheval », par exemple ? La raison est qu’un prédicat unaire est une propriété, et que la relation de subsomption d’un sujet « tombant » sous un prédicat est du même type que la relation d’appartenance d’un élément à un ensemble. Or un ensemble peut lui-même être un élément d’un ensemble d’ordre supérieur : nous l’avons vu avec le cas des valeurs de vérité structurées. Pourquoi donc ne pas contester la distinction absolue de Frege, et admettre que la fonction d’une prédication d’ordre m puisse apparaître comme un objet à part entière dans une prédication d’ordre m+1 ? Rien ne nous en empêche, sinon un préjugé ontologique quant à la nature des individus réels et à condition de bien distinguer les niveaux de prédication du discours (nous nous y sommes employés dans le cas des valeurs de vérité structurées, toujours relatives à un domaine de valeurs Vn).

Allons plus loin encore : pourquoi ne pas inverser la relation extensionnelle de subsomption entre sujet et prédicat (monadique), et affirmer que c’est aux individus de s’expliquer en termes de propriétés, et non l’inverse ? Cette définition descriptiviste des individus consisterait à caractériser chacun d’eux comme une chaîne de bits unique dans laquelle les valeurs booléennes 1 et 0 indiqueraient si l’individu satisfait une propriété ou non. Laissons cette suggestion de côté, et insistons seulement sur le potentiel des valeurs logiques dans le processus de structuration de la pensée.

Concluons par une question d’ouverture : quelle différence y a-t-il entre les valeurs de vérité et les nombres naturels ? Une très grande si, conformément au Principe de bivalence, leur tâche se limite à celle de distinguer deux catégories de proposition : les vraies, et les fausses. Aucune si, conformément au critère de définition (b) vu plus haut, les valeurs de vérité ont le statut de « classes d’équivalence d’énoncés ». En somme, les valeurs de vérité jouent en logique le rôle de noms propres frégéens, d’un ordre très général en logique bivalente et moins général en logique multivalente. En poussant ce stratagème à l’extrême, on pourrait aller jusqu’à concevoir une sémantique dans laquelle chaque proposition aurait sa propre valeur de vérité distincte : un nom propre unique, au sens d’un désignateur rigide à la Kripke. Quelle qu’en soit l’utilité sérieuse pour un logicien, cette procédure aurait tout au moins deux avantages dans le cadre de notre réflexion présente sur la négation. D’une part, elle ferait de la négation cyclique un cas particulier de notre opérateur [Ni] : celui dans lequel la négation s’appliquerait à une valeur donnée pour produire son successeur, au sein d’un domaine de valeurs ordonnées. La logique linéaire y trouverait peut-être sa propre application, ici encore ; mais cela reste à montrer. D’autre part, une sémantique radicale de ce genre est susceptible de donner sens à la « thèse hégélienne » évoquée plus tôt par Granger (1988) : la négation « hégélienne » (ou Aufhebung) ne serait pas un opérateur « appliqué à » des valeurs au sein d’un domaine clos Vx, mais un opérateur « constructeur de » valeurs dans le domaine ouvert des entiers naturels ℕ et comparable à l’opérateur de succession Sn de l’arithmétique de Peano. Tout cela dépasse de loin les propos de Granger sur la négation, tout en résumant assez bien sa philosophie du style : celle d’une structuration d’ordre multiple de la pensée, ordonnée par des règles strictes mais émancipée des normes du sens commun.

Posons-nous deux questions finales, relatives à la raison et à la simplicité.

Le statut de la raison chez Granger reste problématique, partagé entre un aspect pur de la syntaxe et un aspect pratique du style philosophique. À quel point le philosophe peut-il élaborer son propre système de connaissance, et à quel point le logicien est-il libre de concevoir son propre système structuré sans passer nécessairement ?

La notion de simplicité reste elle aussi à justifier, qui repose chez Granger sur une opposition entre les catégories philosophiques de « présence » et d’« absence » d’un objet quelconque (voir la page 6). La bivalence sous-entendue derrière cette dualité philosophique de l’être et du non-être (voir les pages 18 et 19) ici ne suppose-t-elle pas déjà une certaine structure d’ordre préthéorique, réfutant dans le même temps la thèse de simplicité de l’objet logique défendue par Granger ? Un tel problème ne sera pas résolu ici, qui renvoie à la nature des schèmes opératoires et exigerait une discussion bien plus profonde sur l’opposition entre l’épistémologie pure de Kant et l’épistémologie génétique de Piaget. C’est sans doute aux logiciens-philosophes que revient la tâche de répondre à cette difficulté, par la pratique même de leur activité.