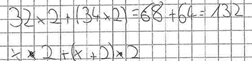Développer la pensée algébrique à travers une activité de généralisation basée sur des motifs (patterns) figuratifs

Vlassis, Joëlle; Demonty, Isabelle; Squalli, Hassane

doi:https://doi.org/10.7202/1055731ar

1. Introduction

Actuellement, l’idée de réduire les apprentissages algébriques à l’application de techniques en utilisant un symbolisme formel a fait son temps. La recherche a démontré depuis longtemps les limites de cette perspective en mettant en évidence les lacunes des élèves en matière de conceptualisation et d’utilisation significative des symboles (Bednarz et Janvier, 1996; Booth, 1984; Kieran, 1992). Il existe depuis lors un consensus croissant pour soutenir l’idée du développement d’une pensée algébrique caractérisée par la présence d’une indéterminée et s’exprimant à l’aide de notations tant formelles qu’informelles (Carraher, Schliemann et Schwartz, 2007; Kaput, 2008; Radford, 2018).

Historiquement, la généralisation constitue le coeur même de l’algèbre et, pédagogiquement, elle joue un rôle important non seulement en algèbre, mais également en arithmétique (Mason, 1996). En effet, d’une part, les activités de généralisation constituent des opportunités intéressantes pour développer cette pensée algébrique dans la mesure où l’expression de la généralité requiert l’utilisation d’une indéterminée. D’autre part, à travers la comparaison de différents moyens de généralisation, ce type d’activité permet d’utiliser de manière significative les techniques algébriques au secondaire, mais également de travailler le sens de l’égalité et des opérations au primaire.

Par ailleurs, Demonty (2017) rappelle que sous l’impulsion des approches socioculturelles l’attention des chercheurs en algèbre se focalise désormais sur les facteurs sociaux considérés comme constitutifs de l’apprentissage. Ceux-ci accordent un intérêt important au rôle médiateur de la culture et des «signes» au sens de Vygotski envisagés comme outils de communication et de pensée, tels que le langage oral, écrit, les symboles formels et informels, les gestes, les schémas, etc. Les activités de symbolisation sont donc importantes pour le développement de la pensée algébrique et constituent un objet essentiel de nos analyses.

Dans ce contexte, le but général de cet article consiste à approfondir la réflexion autour de l’analyse d’une activité de généralisation particulière connue notamment sous le nom de «Carré bordé». Deux objectifs spécifiques sont poursuivis: 1) concevoir une exploitation didactique de cette activité selon une progression dans les processus de raisonnement et de symbolisation et 2) analyser les raisonnements et les symbolisations produits par des élèves.

Cet article est composé de quatre parties. La première discute des caractéristiques de la pensée algébrique et de la pertinence didactique d’activités de généralisation basées sur des motifs (patterns) figuratifs. La deuxième précise tout d’abord les types de raisonnements et de symbolisations généralement observés dans ces activités, puis propose un modèle de la progression du raisonnement et de la symbolisation dans le processus de généralisation (qui a servi de base à l’exploitation de l’activité). La troisième partie développe la séquence d’apprentissage et le contexte de sa mise en place dans les classes. Enfin, la dernière partie analyse les processus de généralisation et de symbolisation développés par les élèves au cours de l’activité.

2. Pensée algébrique et activité de généralisation basée sur les motifs (patterns) figuratifs

2.1 À propos de la pensée algébrique

Depuis de très nombreuses années, l’enseignement et l’apprentissage de l’algèbre représentent un des domaines les plus étudiés en éducation mathématique. Demonty (2017) rappelle que les recherches des années 70 et 80 (voir par exemple l’article synthèse de Kieran [1992]) centrées sur l’analyse des erreurs commises par les élèves du début du secondaire ont montré que ceux-ci éprouvaient d’importantes difficultés dans l’application des techniques et qu’ils n’avaient qu’une compréhension superficielle des procédures algébriques et des concepts de base tels que les lettres, les expressions algébriques ou encore l’égalité. À cette époque, l’algèbre ou le raisonnement algébrique était toutefois intimement lié à l’utilisation du symbolisme algébrique formel s’appuyant sur le code alphanumérique.

Avec l’émergence des approches socioculturelles, les études menées en algèbre font, à partir de la fin des années 90, évoluer l’attention des chercheurs vers les facteurs sociaux et culturels. Dans ce contexte notamment, souligne Demonty (2017), émerge l’idée d’une pensée algébrique qui ne serait plus directement associée à l’utilisation du langage algébrique formel, mais médiatisée par tout type de «signes» (Vygotski, 1997), incluant le langage oral, les mots, les symboles mathématiques, les notations non conventionnelles ou encore les gestes.

Parallèlement, apparaît l’idée de développer une pensée algébrique dès l’école primaire — puisque cette pensée peut s’affranchir des notations formelles — dont l’objectif n’est pas d’introduire précocement l’algèbre, mais d’approfondir dès l’école primaire la compréhension de concepts mathématiques fondamentaux comme le sens des opérations ou de l’égalité, eux-mêmes liés au développement de la pensée algébrique (Kaput, 2008; Squalli, Mary et Marchand, 2011).

La perspective du développement précoce de la pensée algébrique, c’est-à-dire avant l’introduction du symbolisme formel de l’algèbre, amène à définir la pensée algébrique autrement que par la présence des signes alphanumériques. Nous reprenons à Radford (2014) les caractéristiques d’une pensée algébrique:

L’indéterminée: Le problème implique des nombres non connus (inconnues, variables, etc.).
La dénotation: Celle-ci consiste à nommer ou symboliser cette indéterminée. Cette dénotation peut se faire de différentes manières: à l’aide du code alphanumérique, mais aussi à l’aide du langage naturel, des gestes ou de signes non conventionnels.
L’analycité: Celle-ci consiste à traiter les quantités indéterminées comme si elles étaient connues et à parvenir à réaliser des opérations sur ces nombres inconnus.

2.2 Développer la pensée algébrique par une activité de généralisation basée sur des motifs (patterns) figuratifs

Les activités de généralisation sont considérées par de nombreux auteurs (Mason 1996; Radford, 2008) comme des opportunités fondamentales pour développer la pensée algébrique puisqu’elles favorisent un raisonnement visant à faire identifier et exprimer des régularités. Ces activités répondent aux critères d’une pensée algébrique dans la mesure où leur objectif consiste à formuler un moyen général au départ d’une indéterminée, en l’occurrence d’une variable. Ces activités invitent à exprimer les généralités produites et leurs justifications dans un langage tout d’abord non conventionnel et qui tend à devenir de plus en plus conventionnel au fil des nécessités de l’activité.

Dans le cadre de cet article, nous développons une activité de généralisation issue de l’activité du «Manufacturier» (Bednarz, 2005), appelée également «Carré bordé» (Coulange et Grugeon, 2008; Coppé et Grugeon, 2009), dont un exemple est présenté ci-dessous. Il s’agit de trouver le nombre de carrés grisés de la bordure quel que soit le nombre de carrés du côté du carré blanc (n).

Cette activité n’est pas nouvelle; elle a été utilisée à plusieurs reprises dans le passé (Bednarz, 2005; Coppé et Grugeon, 2009; Coulange et Grugeon, 2008; Denis et al., 2004; Vlassis et Demonty, 2002). Ce qui est neuf, en revanche, c’est le type d’exploitation proposé ainsi que les analyses des processus de raisonnement et de symbolisation d’élèves avant et après l’apprentissage de l’algèbre.

Les activités de généralisation basées sur des supports schématiques, appelés également «patterns figuratifs», constituent un contexte particulièrement riche pour travailler la pensée algébrique avec les élèves tant au primaire qu’au secondaire. L’intérêt majeur de ce type d’activité réside dans la diversité des expressions possibles de la généralisation. En effet, les différentes visualisations possibles des figures vont entraîner différents calculs et différentes expressions selon les régularités identifiées.

Les différentes expressions de la généralisation issues de ces visualisations favoriseront des débats riches. En outre, les élèves pourront argumenter les moyens de généralisation trouvés en s’appuyant sur les dessins.

3. Processus de raisonnement et de symbolisation dans la généralisation

3.1 Les raisonnements

Radford (2006, 2008) a identifié trois types de raisonnements des élèves dans la généralisation issue du contexte de suites arithmétiques. Nous les résumons brièvement ici.

3.1.1 L'«induction naïve»

L’«induction naïve» consiste à rechercher un motif inconnu en analysant les caractéristiques d’un seul motif connu ou en identifiant de manière incorrecte la structure du motif.

Dans le cas de l’activité du carré bordé, il s’agirait, par exemple, de considérer que si pour un carré de 3 carrés blancs de côté il faut 16 carrés grisés, alors pour un carré de 6 carrés blancs de côté il en faudra le double, c’est-à-dire 32. On applique ainsi la proportionnalité de manière inadéquate.

3.1.2 La «généralisation arithmétique»

Dans la «généralisation arithmétique», la personne identifie un point commun à travers l’analyse de plusieurs termes de la suite. Il s’agit de l’accroissement constant entre les termes consécutifs (par exemple, ajouter chaque fois 2 à chaque terme consécutif, comme dans l’exemple de la figure 1), c’est-à-dire de la mise en évidence de la «raison». Cette généralisation permet de prédire les cas proches. Cependant, un tel raisonnement empêche l’élève de déterminer un terme lointain à partir d’un terme déjà connu en ne prenant en considération «qu’un seul élément» de la régularité, en l’occurrence la raison. Ce type de généralisation apparaît fréquemment dans le cas de suites arithmétiques dont les motifs (patterns) figuratifs sont présentés dans un ordre croissant, comme dans l’exemple suivant:

Exemple de suite arithmétique dont les motifs (patterns) figuratifs sont présentés dans un ordre croissant (Radford, 2006, p. 5) — Figure 1

**Exemple de suite arithmétique dont les motifs (*patterns*) figuratifs sont présentés dans un ordre croissant (Radford, 2006, p. 5)**

Elle peut apparaître également dans le cas du carré bordé chez des élèves qui pointeraient que:

pour un carré de 2 carrés blancs de côté il faut 12 carrés grisés;
pour un carré de 3 carrés blancs de côté il faut 16 carrés grisés;
et que, donc, pour un carré de 4 carrés blancs de côté il en faudra 4 de plus, à savoir 20 carrés grisés.

3.1.3 La «généralisation algébrique»

Dans la «généralisation algébrique», l’élève identifie une régularité à travers l’analyse de quelques termes de la suite qu'il peut ensuite généraliser pour tous les termes de la suite. Dans le cas du «carré bordé», l’élève se base sur la mise en relation de «deux éléments»: le nombre de carrés blancs sur un côté et le nombre de carrés grisés correspondant (basé sur l’analyse du dessin). Cette régularité est ensuite étendue aux autres termes de la suite.

Dans le «carré bordé», un raisonnement de type «généralisation algébrique» serait par exemple de «voir» que le nombre de carrés blancs sur le côté est repris quatre fois sur le contour des carrés grisés auxquels il faudra ajouter les quatre carrés des coins (4. n+4).

3.2 Les symbolisations

Dans les démarches d’induction naïve ou de généralisation arithmétique, les élèves expriment le plus souvent leur raisonnement à l’aide de calculs, de phrases, d’annotations sur le dessin ou d’un substitut symbolique pour identifier le nombre inconnu. Dans la généralisation algébrique, Radford (2008) observe que les élèves peuvent proposer trois types de symbolisation: factuelle, contextuelle et symbolique. Dans la «généralisation factuelle», la variable est symbolisée à partir d’un nombre. Dans la «généralisation contextuelle», la variable est symbolisée par un substitut symbolique (un point d’interrogation, un cadre vide, une marque voire une lettre), mais la symbolisation élaborée garde des traces de la situation qui l’a vue naître. La «généralisation algébrique symbolique» se détache quant à elle de la situation pour proposer une écriture tout à fait correcte sur le plan mathématique. Dans ce cas, la formulation symbolique de la généralisation ne comporte aucune trace permettant de relier les symboles à leurs signifiants.

L’intérêt du modèle de Radford (2008), tant pour les raisonnements que les symbolisations de la généralisation, réside dans le cadre d’analyse qu’il propose pour comprendre le raisonnement et les erreurs des élèves lorsqu’ils généralisent un processus.

3.3 Le développement du processus de généralisation: le modèle de Dörfler (1991)

Squalli (2015) développe le cadre d’analyse de Dörfler (1991) en poursuivant un objectif différent de Radford (2008). Il ne s’agit plus d’observer des raisonnements ou des modes d’expressions, mais de décrire le développement «idéal » du processus même de généralisation algébrique. Ce modèle permet de comprendre la structuration des différentes étapes possibles, nécessaires à la progression vers une généralisation algébrique au sens proposé par Radford (2008), et d’analyser l’évolution des élèves dans le processus de généralisation.

Le schéma ci-dessous (figure 2), proposé par Squalli (2015), reprend les principales étapes de ce processus:

Figure 2

**Modèle simplifié de généralisation théorique de Dörfler (1991) proposé par Squalli (2015)**

Dans ce modèle, Squalli (2015) rappelle que le point de départ est une «action» ou un «système d’action à partir d’une situation» dont l’objectif consiste à orienter l’attention du sujet vers certaines relations entre les objets sur lesquels portent ces actions. La répétition de ces actions conduit le sujet, sur la base d’une «réflexion sur ce système», à une certaine constance dans les actions qui l’amène à prendre conscience de certains «invariants» essentiels des actions dont la «formulation» nécessite une description symbolique que ce soit verbalement ou de manière iconique, géométrique ou algébrique. Un moment crucial dans le processus de généralisation se produit quand ces invariants sont remplacés par des «prototypes», c’est-à-dire quand la formulation des protocoles ne sert plus uniquement à décrire les cas spécifiques examinés, mais aussi à envisager les cas potentiels. Enfin, les invariants et leurs formulations symboliques sont détachés des actions originales. Dès le départ, les symboles possèdent un certain domaine de référence et ce domaine est étendu graduellement. Les symboles acquièrent les caractéristiques d’objet. Ces symboles sont alors de nouveaux objets de la pensée, des objets mathématiques dont la signification réside dans les invariants. Le détachement total des actions originales consiste à produire une formule correcte et qui ne conserve plus la trace des éléments de contexte.

3.4 Modèle présentant le développement de la symbolisation: Signes et chaînes de signification

L’introduction des approches socioculturelles en éducation mathématique a mis en lumière l’importance des processus sociaux dans les apprentissages. Si cette importance a également été soulignée dans d’autres paradigmes de recherche, ceux-ci sont considérés comme consubstantiels à l’apprentissage dans les approches socioculturelles. Dans ces dernières, le développement cognitif trouve son origine dans les interactions sociales médiatisées, c’est-à-dire instrumentées ou outillées par des signes, comme déjà évoqué précédemment.

Les approches socioculturelles nous amènent à considérer le signe dans la foulée de sémioticiens, comme exprimant une relation étroite et sémantique entre signifiant et signifié. Un signe est ainsi représenté comme un ensemble composé de deux facettes inséparables. Cependant, de notre point de vue, cette conception du signe ne peut suffire. Dans les approches socioculturelles, un signe n’est jamais une entité pour elle-même, il prend place et fait sens dans un contexte «d’activité» précis et est produit pour atteindre un objectif donné (Radford, 1998). Selon Radford, l’activité, envisagée comme l’environnement dans lequel s’insèrent les actions mathématiques des individus et qui les rend nécessaires présente deux caractéristiques importantes. La première, c’est qu’elle est médiatisée par les signes et est donc enracinée dans la culture. La seconde, c’est qu’elle est orientée vers un but.

Ainsi, de notre point de vue, un signe se définit 1) par un signifiant et un signifié en étroite relation, 2) comme élément médiatisant une activité donnée orientée vers un but. C’est pourquoi nous suggérons de compléter la représentation du signe proposée par la sémiotique en l’intégrant au coeur même de l’activité dans laquelle il est produit (voir figure 3).

Figure 3

**Proposition de définition du «signe» incluant la notion d’activité**

Plusieurs auteurs (Gravemeijer, Cobb, Bowers et Whitenack, 2000; Presmeg, 2006) ont mis en évidence le rôle crucial des activités de symbolisation qui se développent en relation avec l'évolution de pratiques mathématiques de la classe afin de faire émerger une réalité mathématique abstraite. Selon ces auteurs, les différentes étapes de symbolisation constituent une chaîne de significations dont la composante de base est le signe. L’avantage de ce processus, selon Presmeg (2006), c’est qu’à chaque point de la chaîne existe la possibilité pour les élèves de revenir en arrière, y compris aux actions initiales. Le schéma présenté dans la suite (voir figure 5) propose une chaîne de significations incluant la notion d’activité, absente chez les auteurs précités. Cette chaîne met en évidence cette évolution du signe, rendue nécessaire par des activités de complexité croissante (Vlassis, 2010; Vlassis et Demonty, 2018).

4. Méthodologie

4.1 Présentation de la séquence - Objectif 1

La figure 4 présente l’activité telle qu’elle a été soumise aux élèves.

Figure 4

**Activité «Antoine fait des mosaïques» telle que proposée aux élèves (Demonty et Vlassis, 2018)**

Si la structure du questionnement n’est pas neuve — on la retrouve notamment chez Coulange et Grugeon (2008) — c’est le regard porté sur ce questionnement grâce aux apports combinés du modèle de Dörfler (1991) et des chaînes de signification qui est neuf. L’apport de Dörfler met en avant les étapes par lesquelles l’enfant doit passer pour avancer dans le processus de généralisation tandis que la structuration en une chaîne de signification oriente l’attention vers le développement de la symbolisation depuis les manipulations concrètes jusqu’à la formulation de la généralité en langage mathématique. La figure 5 présente le développement des étapes de cette activité (en relation avec les questions posées) selon ces cadres théoriques.

Figure 5

**Modèle de la structuration de l’activité basé sur les apports de Dörfler (1991) et des chaînes de significations (Vlassis et Demonty, 2018)**

Plus précisément, la question 1 oriente les élèves vers le dénombrement physique du nombre de carrés formant le contour de la mosaïque qu’ils sont appelés à construire. La question ne nécessite pas et n’invite pas à un dénombrement raisonné, bien que certains élèves peuvent le faire. Le schéma implicite du dénombrement utilisé est le protocole d’un système d’actions initial qui devrait être transparent pour les élèves. La question 2 invite les élèves à répéter le système d’actions initial pour un autre exemple spécifique, mais cette fois-ci la consigne consiste à faire trouver un calcul; elle oriente ainsi les élèves à porter leur attention au protocole des actions (le schéma de dénombrement) et non plus au dénombrement lui-même. Dans la question 3, les élèves ne peuvent plus réaliser physiquement le dénombrement (le matériel n’est pas suffisant), ils doivent donc le réaliser mentalement. La taille relativement grande de la mosaïque à 32 carrés de couleurs a pour but de «forcer» les élèves à expliciter le protocole des actions utilisé pour les cas précédents pour l’adapter au cas présent ou encore à faire un dénombrement raisonné utilisant les cas précédents pour valider la justesse du dénombrement. Les élèves sont ainsi mis dans la situation où ils doivent dégager des invariants à partir des deux cas précédemment examinés et étendre ces invariants au nouveau cas. La justesse de la réponse ne peut plus reposer sur un argument empirique (dénombrement physique), mais sur les invariants dont les significations renvoient au système d’actions initial.

La question 4 amène les élèves à anticiper les cas potentiels. Dans cette situation, les invariants ne peuvent plus référer à des cas spécifiques, mais à des cas potentiels non spécifiés. La question amène les élèves à transformer les invariants en prototypes, les cas spécifiques précédents deviennent alors chez les élèves des exemples génériques. La généralité peut être formulée de manière libre soit en utilisant le langage ordinaire ou un langage mixte constitué de symboles mathématiques et non mathématiques soit en recourant au langage formel. Finalement, la question 5 invite les élèves à réfléchir sur la formulation symbolique de la généralité et à représenter de manière explicite et mathématique la variable. Cette formulation est alors détachée du système d’actions initial et peut se prêter à des manipulations syntaxiques en cohérence avec les règles du calcul et sans lien avec les signifiants.

4.2 Contexte d’implémentation de l’activité

Cette activité a été proposée dans le courant du mois de janvier 2016 dans deux classes de secondaire technique, l’une de 1^re année (grade 7) avec 14 élèves et l’autre de 2^e année (grade 8) avec 20 élèves. Cette activité était une première pour les élèves des deux niveaux scolaires. Si les élèves de grade 8 suivaient un cours d’algèbre depuis près d’un an et avaient été initiés dans ce contexte à la résolution des équations et aux techniques algébriques comme la réduction de termes semblables, la distributivité, etc. – ils maîtrisaient donc «l’algèbre» impliquée dans l’activité — les élèves de la classe de 1^re secondaire (grade 7) n’avaient reçu aucun enseignement de l’algèbre.

Deux moments étaient planifiés. Deux périodes de temps (2x50’) ont d’abord été consacrées au travail en groupes pour répondre aux différentes questions de l’activité, puis deux autres périodes de temps (2x50’) ont été consacrées à la mise en commun. Cinq groupes (quatre de trois élèves et un de deux élèves) ont été formés en 1^re année (notés G1-1, … , G1-5) et sept groupes (six de trois élèves et un de deux élèves) en 2^e année (notés G2-1, … , G2-7).

Nos analyses sont issues des deux premières périodes, pendant lesquelles les élèves travaillaient en groupes. L’enseignante a lancé le travail et n’a donné que très peu de consignes concernant la tâche à réaliser, si ce n’est les consignes d’organisation. L’enseignante et deux chercheurs passaient dans les groupes et aidaient ceux qui étaient en difficulté. Les élèves des deux classes étaient répartis en groupes de trois ou de deux. Les données ont été collectées sur la base des productions écrites des différents groupes d’élèves et d’enregistrements audio ou vidéo des interactions des élèves dans les différents groupes. Il convient de souligner que les élèves n’avaient jamais résolu de problèmes de généralisation. C’était leur premier contact avec ce type de tâche. Pour soutenir les premières actions des élèves, l’enseignante avaient mis à leur disposition du matériel concret pour représenter les mosaïques.

4.3 Questions de recherche — Objectif 2

Le deuxième objectif de cet article consiste à analyser les processus de généralisation et de symbolisation qui ont accompagné la production des messages dans l’activité «Antoine fait des mosaïques». Plus précisément, il vise à répondre aux deux questions recherche suivantes:

Quel raisonnement développent les élèves dans leur processus de généralisation et quelles difficultés rencontrent-ils?
Quels types de symbolisation développent les élèves et quelles difficultés rencontrent-ils?

5. Résultats

Les résultats sont structurés autour de deux axes principaux en relation avec les deux questions de recherche formulées ci-dessus. Le premier axe porte sur les raisonnements dans le processus de généralisation, c’est-à-dire les différents systèmes d’actions et invariants produits par les élèves. Le second concerne l’analyse des symbolisations produites par les élèves.

5.1 Analyse des raisonnements dans le processus de généralisation

5.1.1 Systèmes d’actions initiaux et invariants correspondants

Cette analyse se base sur l’expression finale de la généralité (questions 4 et 5 de la figure 4) de chaque groupe en 1^er et 2^e années du secondaire et identifie le système d’actions sur lequel elle repose.

L’ensemble des élèves a utilisé différents systèmes d’actions qui peuvent être configurés en quatre grandes familles (F1, F2, F3 et F4). Une famille étant une classe constituée des systèmes d’actions portant sur les mêmes objets et conduisant ainsi aux mêmes invariants. Voici dans le tableau 1 les familles identifiées dans la situation «Antoine fait des mosaïques».

Tableau 1

**Familles de systèmes d’actions identifiées par les élèves**

Le tableau 2 présente la répartition des groupes d’élèves selon les familles.

Tableau 2

**Familles de systèmes d'actions identifiés par les différents groupes**

La majorité des groupes, qu’ils soient de 1^re année ou de 2^e année, est parvenue à produire une généralisation algébrique. Seul un groupe de 2^e année (G2-5) ne parvient à pas à produire un système d’actions et à aller au-delà de la première question. Les tableaux 1 et 2 témoignent également de la variété des démarches développées par les élèves, surtout en 1^re année, même si ce sont essentiellement les familles F1 et F3 qui ont été plébiscitées.

Cependant, de grandes différences de niveau ont été observées parmi les groupes en ce qui concerne la réflexion pour aboutir à la production du message de généralisation. En effet, certains groupes (notés par un astérisque) ont compris rapidement l’enjeu de l’activité (alors que ce type d’activité n’avait jamais été proposé auparavant dans la classe) et trouvé facilement un prototype, c’est le cas des groupes G1-2 et G1-5 et des groupes G2-1 et G2-3, tandis que les autres groupes ont eu besoin d’un support soutenu de l’enseignante pour arriver à trouver les invariants et à produire le moyen général. Pas moins de quatre approches différentes ont été mobilisées par les élèves de 1re année et deux par ceux de 2^e année. Cette diversité dans les démarches des élèves témoigne du potentiel de ce type d’activité pour le développement des apprentissages algébriques, dans la mesure où la comparaison de ces différentes formules ou expressions permettra de (re)travailler le sens des opérations arithmétiques ainsi que des concepts comme le signe d’égalité, la notion de variable et des techniques comme la réduction de termes semblables, la distributivité, voire les produits remarquables.

5.3.2 Difficultés des élèves dans le processus de généralisation

Deux difficultés principales ont été identifiées chez les élèves dans le processus de généralisation. D’abord, certains élèves ont rencontré des difficultés à identifier les invariants. En particulier, les élèves des groupes G2-6 et G2-7 ont commis tous deux la même erreur à la question 2 où il fallait produire un calcul pour une mosaïque qui compterait sept carrés colorés de côté. La réponse à la question 1, où il s’agissait de produire un modèle à l’aide du matériel pour une mosaïque de cinq carrés colorés, ne leur avait posé aucune difficulté. Mais pour répondre à la question 2, les élèves des deux groupes ont produit le calcul 9 x 4 sans penser à contrôler leur réponse par le dénombrement. L’erreur de ces élèves semble venir d’une compréhension de la situation basée sur une visualisation du motif (pattern) figuratif en termes de périmètre: en effet, les carrés blancs correspondent visuellement au contour de la figure. Puisqu’il est demandé de produire un calcul pour trouver le nombre de carrés blancs autour des carrés colorés, les élèves pensent qu’il s’agit d’appliquer la formule du périmètre, en l’occurrence «côté x 4». Nous pensons que le problème pour ces élèves réside dans un glissement de leur centre d’attention dans l’analyse du dessin. Sans s’en rendre compte, ceux-ci sont passés du dénombrement de carrés en tant qu'unité d’aires au dénombrement des carrés comme unités de longueur. Ces élèves ont ainsi considéré les côtés externes des petits carrés dont la somme correspond au périmètre de la mosaïque. Dans cette perspective, les côtés externes des carrés placés aux quatre coins sont bien au nombre de deux. L’enseignante est intervenue dans les deux groupes pour aider les élèves à changer de point de vue, en leur faisant vérifier la réponse de leur calcul par dénombrement. Ce fut très difficile. Les élèves ne voyaient pas pourquoi leur calcul ne conduisait pas à la réponse correcte. Il a fallu plusieurs interventions de la part de l’enseignante pour que les élèves comprennent leur erreur.

Ensuite, certains groupes ont éprouvé des difficultés à étendre le domaine de référence et à établir un prototype. Les groupes G1-1 et G1-5 identifient correctement les invariants à la question 2 (pour 7 carrés colorés de côté), mais n’utilisent pas la réflexion qui a conduit à l’émergence de ces invariants pour trouver le calcul qui donnera le nombre de carrés blancs à la question 3 (32 carrés colorés de côté). Prenons l’exemple du groupe G1-5. Celui-ci produit assez rapidement le calcul basé sur la différence des aires (F4), 9 x 9 – 7 x 7 en réponse à la question 2. Cependant, pour la question 3 avec les 32 carrés colorés de côtés les élèves commencent par trouver 8 x 4, car «8 x 4, ça fait 32», puis tentent de réaliser la mosaïque avec les 32 carrés colorés de côté. Puisqu’il manque de cubes, ils réalisent, avec les carrés disponibles, un rectangle qui ne correspond évidemment plus à la structure des mosaïques proposée dans l’activité. Ils demandent alors l’aide de l’enseignante. L’enseignante essaie de les mettre sur la bonne voie en leur rappelant leur raisonnement à la question 2 puis s’en va. À ce moment, un élève pense à calculer 32 x 32, mais un autre élève du groupe explique qu’il a calculé 4 x 8, car 32 divisés par 8 donnent 4. L’élève qui avait cherché 32 x 32 trouve la réponse 1024. Comme il n’y a pas d’accord dans le groupe à propos de ce qu’il convient de faire, les élèves font de nouveau appel à l’enseignante qui permet à leur réflexion d'aboutir à la généralisation basée sur la différence d’aires (famille F4).

Les échanges dans les deux groupes montrent à quel point ce fut difficile pour ceux-ci de parvenir à déterminer les prototypes, c’est-à-dire à généraliser le processus dont ils semblaient pourtant avoir identifié les invariants dès la question 2. Cependant, dans les deux groupes, la réponse à la question 2 se base encore sur l’analyse du matériel, comme en témoignent leurs interactions (non rapportées ici). À la question 3, il n’est plus possible d’utiliser les petits cubes, car ils ne sont plus assez nombreux. La réflexion doit devenir plus abstraite: il faut s’imaginer un cube de 32 carrés colorés de côté. C’est véritablement lors de la réflexion sur cette question que les élèves se voient obligés de réfléchir à la structure du schéma et aux relations entre les différents éléments sans le support concret du matériel. On peut considérer que cette étape est déterminante dans l’identification d’un prototype.

5.2 Analyse des symbolisations des moyens de généralisation

Dans cette section, nous présentons l’analyse des symbolisations des questions 4 et 5 qui concernent le processus de généralisation en tant que tel. Rappelons que la question 4 demandait de trouver un moyen de généralisation sans en préciser la forme, tandis que la question 5 demandait d’écrire ce moyen en langage mathématique.

Le tableau 3 présente les différentes symbolisations des généralisations algébriques produites par les élèves.

Analyse des symbolisations des généralisations algébriques, sur la base du modèle de Radford (2008)1 — Tableau 3

**Analyse des symbolisations des généralisations algébriques, sur la base du modèle de Radford (2008)[1]**

L’analyse de ce tableau révèle sans surprise que seuls les élèves de 2^e année parviennent à produire une «généralisation algébrique symbolique». Cela concerne les groupes G2-3 et G2-7. La «généralisation factuelle», quant à elle, concerne deux groupes de 1^re année, G1-3 et G1-5, n’ayant encore jamais abordé l’algèbre.

Un groupe de 2^e année (G2-4) ne répond pas à la question 5 qui demande de rédiger le moyen en langage mathématique. Il ne produit ni même ne tente de rédiger aucune formule ni calcul, alors que ces élèves apprennent l’algèbre depuis un an. Dans la suite, nous analysons l’expression des différents types de généralisation algébrique.

5.2.1 Généralisation algébrique factuelle

La figure 6 présente la production du groupe G1-3. La généralisation est de type 4 (x + 1) (Famille F2) et se prête à la même analyse que celle du groupe G1-5 également concerné par ce type de généralisation (voir tableau 3).

Figure 6

**Généralisation algébrique factuelle proposée par le groupe G1-3**

Cet exemple présente la généralisation spontanée produite par le groupe. On constate que tant l’expression générale en mots que celle en langage mathématique portent sur un seul exemple. Cependant, le terme «exemple», placé devant les deux expressions, témoigne du caractère général de ce cas numérique, qui n’est là que pour expliquer une façon générale de procéder. Les exemples choisis dans les deux modes d’expression sont par ailleurs différents. Après une discussion avec l’enseignante pour les mener vers la formule, ces élèves en sont venus à la production finale suivante (figure 7).

Figure 7

«Formule» finale proposée par le groupe G1-3

-> See the list of figures

5.2.2 Généralisation algébrique contextuelle

Le tableau 4 présente les différentes formules de généralisation contextuelle présentées par les différents groupes.

Formules de généralisation contextuelle proposées par les groupes de 1re et 2e années — Tableau 4

**Formules de généralisation contextuelle proposées par les groupes de 1^re et 2^e années**

Notons que deux groupes (G1-1 et G2-4) proposent des généralisations contextuelles, mais en mots uniquement. Ils ne sont donc pas repris dans ce tableau.

Les formules produites par les cinq groupes présentés dans le tableau sont contextuelles dans la mesure où elles portent toutes la marque des actions posées par les élèves pour généraliser. Par exemple, les parenthèses (G1-2) servent à montrer la hiérarchie des opérations (on multiplie d’abord x par 4 puis on ajoute 4), l’utilisation de deux lettres dans l’expression a+b+a+b vise à exprimer deux nombres différents (autrement dit les deux grands côtés et les deux petits [G2-2]) ou encore le signe «·» reste apparent pour indiquer la multiplication (G2-6).

En 1^re année, examinons comment l’enseignante amène le groupe G1-4 à produire une formule. La généralisation du groupe G1-4 est de la famille F3, c’est-à-dire de type 2.(x+2)+2.x.

La figure 8 présente l’expression du moyen général qu’ils ont trouvé.

Figure 8

**Généralisation algébrique contextuelle proposée par le groupe G1-4**

La formule proposée ce groupe a été produite avec l’aide de l’enseignante. La formule a été rédigée à la suite de discussions entre l’enseignante et les élèves à propos du calcul 32 x 2 + (34 x 2) = … comme présenté dans la figure 9.

Figure 9

«Formule» finale proposée par le groupe G1-4

-> See the list of figures

Voici un extrait des interactions à propos du processus soutenues par l’enseignante (P).

1 P

Et si j’avais mis 180, quel calcul est-ce qu’on devrait faire?

2 E2

180 x 2 plus 182 x 2

3 P

Et maintenant, si on veut une formule qui fonctionne avec n’importe quel nombre de carrés de couleur, comment trouver une formule qui va marcher dans tous les cas?

4 E2

… avec des phrases?

5 E3

… on peut aussi faire des calculs ici pour expliquer…

6 P

Vous n’êtes pas loin de trouver le calcul, il faut juste remplacer le 32 et le 34 par quelque chose qui fait que ça marche tout le temps… si je prenais le 200, on va appliquer la formule, si je prenais 500 ça marcherait aussi

7 E2

Alors on fait x × 2

8 P

Oui… très bien x × 2

9 E3

Ah oui… x × 2 et après…

10 E2

… oui plus…

11 P

Tu continues la formule, très bien.

12 E3

Plus x × 4, euh × 2 aussi

13 E2

x fois… non… plus quatre

14 P

Non le 34, il a quel lien avec le 32?

15 E2

plus deux… alors plus x + 2

16 P

Bien

17 E2

… × 2

18 E3

Ok, x . 2 plus… [E3 écrit la formule juste en dessous du calcul, après avoir changé les symboles «fois» par un point]

Guidés par l’enseignante, les élèves (qui n’ont reçu encore aucun cours d’algèbre au secondaire) parviennent à rédiger la formule. Notons que les élèves hésitent lorsqu’il s’agit d’exprimer le nombre de carrés blancs sur le grand côté qui correspond dans leur calcul au nombre 34 (lignes 12 et 13). Pour les amener à produire x + 2, l’enseignante doit mettre en évidence le lien entre les nombres 32 et 34 (ligne 14). Cette difficulté, assez répandue et rencontrée également par les élèves de 2^e année, correspond à ce que Duval (2002) appelle «la redésignation fonctionnelle». La formule finale prend tout son sens pour les élèves en relation avec le calcul posé dans l’activité (32 x 2 + 34 x 2). Il s’agit d’une première étape dans la symbolisation algébrique et celle-ci reste encore profondément ancrée dans le contexte.

Du côté des élèves de 2^e année, deux types d’erreurs ont été observés dans la production de leur formule.

La difficulté d’exprimer une variable en fonction d’une autre dans l’expression produite par le groupe G2-2. Cette difficulté renvoie au concept de «redésignation fonctionnelle», défini par Duval (2002), qui concerne la nécessité, notamment dans les problèmes impliquant les équations, de choisir une lettre qui permettra de désigner non pas une, mais plusieurs quantités exprimées dans l’énoncé. Dans le cas du groupe G2-2, celui-ci formule l’expression a+b+a+b, plutôt que la formule x+2+x+x+2+x.
La deuxième concerne le groupe G2-6, mais aussi le groupe G2-1 qui, dans une première version, avait écrit la formule 4.a+4.b remplacée dans la suite par 4.a+4.1. Les expressions produites témoignent d’une confusion entre les constantes et les variables. De même, le groupe G2-6 avait tout d’abord produit 4.a+b, clairement visible sous les hachures, avant de rédiger 4.a+4.

5.2.3 Généralisation algébrique symbolique

La figure 10 présente la formule finale proposée par les groupes G2-3 et G2-7.

Ce sont les deux seuls groupes qui ont pensé à réduire les expressions. Dans les deux cas, les élèves ont d’abord produit une expression mathématiquement correcte, mais encore calquée sur les actions posées. Ils semblent ensuite s’être détachés du contexte et l’ont simplifiée comme toute autre expression algébrique. Dans cette dernière action, le contexte s’efface pour faire place à l’expression algébrique pour elle-même. Pour Dörfler (1991), il s’agit du «détachement des invariants de leur véhicule original». Pour Radford (2008), la généralisation algébrique symbolique se détache quant à elle de la situation, pour proposer une écriture tout à fait correcte sur le plan mathématique, qui n’est plus enracinée dans le contexte de la suite. Notons que le groupe G2-3 utilise la majuscule plutôt que la minuscule qui correspond à l’usage en mathématiques. S’agit-il du symbole N représentant les naturels? Dans ce cas, le N représenterait-il un nombre naturel? Dès lors, les élèves ne seraient pas dans un détachement total. Il est difficile d’avoir une certitude à ce sujet. On peut cependant considérer que le fait de réduire l’expression, même en utilisant une majuscule, implique un changement de perspective où l’élève passe d’une description des actions posées à une réflexion sur l’objet même de cette expression pour la réduire. Malgré une expression réduite et correcte sur le plan mathématique, il n’est pas certain que les élèves aient réellement produit une généralisation algébrique symbolique ou soient arrivés au détachement total. Pour en être convaincu, il faudrait s’assurer que les élèves puissent considérer d’autres formules de généralisation comme équivalentes à la leur.

6. Discussion et conclusion

Cet article visait à proposer une exploitation d’une activité de généralisation sur la base d’un modèle intégrant une progression des raisonnements dans le processus de généralisation selon Dörfler (1991) en relation avec une structuration des symbolisations selon une chaîne de significations (Gravemeijer et al., 2000; Vlassis et Demonty, 2018). Il proposait également d’analyser les raisonnements et les symbolisations des élèves qui ont travaillé à cette activité.

Du point de vue des raisonnements dans le processus de généralisation (question de recherche 1), les résultats de l’expérimentation de cette séquence nous conduisent à mettre en évidence trois constats principaux.

Tout d’abord, certains groupes d’élèves, tant de 1^re année que de 2^e année, ont rapidement perçu les enjeux de l’activité et de sa structuration. Ils ont rapidement identifié les invariants et déterminé un prototype sur la base des schémas proposés dans l’activité. La principale préoccupation résidait alors dans la symbolisation de cette généralisation.

Ensuite, d’autres groupes ont eu besoin d’un support important de l’enseignante. Certains ont éprouvé de grandes difficultés dès la question 2 en cherchant à identifier les invariants pour produire le calcul requis. Ils proposaient 9x4 comme s’il s’agissait d’un périmètre. On peut considérer cette démarche comme relevant de «l’induction naïve» au sens de Radford (2008), dans la mesure où l’invariant identifié (périmètre) est erroné: l'unité de mesure du dénombrement est le carré et non son côté.

Enfin, la structuration de la séquence impose à la question 3 d’abandonner le matériel et confronte les élèves à l’expression des invariants. Plusieurs groupes, qui pourtant avaient réussi sans difficulté apparente à répondre à la question 2, ont été «déséquilibrés» au sens de Piaget dans la mesure où il ne leur était plus possible d’utiliser le matériel pour résoudre le problème posé. C’est à cette étape que les élèves, contraints de produire une opération sans le support du matériel, sont amenés à réfléchir sur leur système d’actions et à réellement identifier les invariants. Deux hypothèses peuvent être avancées concernant ces difficultés. Premièrement, il se peut que ces groupes n’aient pas perçu la structuration de la séquence et aient interprété la question 3 comme une question d’une autre nature que la question 2. Il est possible que ces élèves respectent ainsi inconsciemment des règles métadiscursives (Sfard, 2001; van Oers, 2001; Verschaffel, Greer et De Corte, 2000) qui renvoient à ce que Brousseau (1997) appelle le «contrat didactique». En l’occurrence, confrontés aux différentes questions de l’activité, ces élèves qui n’ont pas établi de lien entre les questions 2 et 3 peuvent très bien avoir compris qu’il s’agissait de questions de natures différentes, comme cela se produit traditionnellement lorsqu’ils doivent effectuer une liste d’exercices. La deuxième hypothèse, que nous privilégions, consiste à penser que ces élèves n’auraient pas pris clairement conscience de leur système d’actions dans la question 2 et n’auraient donc pas vraiment identifié les invariants.

Du point de vue de la symbolisation (question de recherche 2), l’utilisation de motifs (patterns) figuratifs a entraîné les élèves à produire un large éventail de formules de généralisation sur la base de différents systèmes d’actions résultants de différentes visualisations des motifs (patterns).

Deux constats importants émergent des résultats. Tout d’abord, la majorité des élèves parviennent à produire des formules en langage mathématique même si la plupart restent à un niveau «contextuel». Cependant, pour les élèves de 1^re année, il s’agit d’un important pas en avant étant donné que l’activité constituait leur première rencontre avec l’algèbre. La formule contextuelle émerge, dans ce contexte, des processus d’actions développés par les élèves et est calquée sur les opérations. Ensuite, soulignons qu’en 2^e année, seuls deux groupes sont parvenus à la généralisation algébrique symbolique. L’enseignante de cette classe s’est montrée surprise que davantage de groupes ne soient pas parvenus à produire la formule correcte sur le plan mathématique. Il semble que ces groupes n’aient pas nécessairement établi de lien entre l’algèbre qu’ils travaillaient habituellement en classe et l’activité proposée. Il faut être cependant conscient que l’activité de généralisation dans laquelle les élèves étaient engagés requiert de leur part une utilisation de l’algèbre très différente de celle qu’ils ont l’habitude de développer. Il s’agit ici non pas d’appliquer une technique algébrique fortement développée dans les classes, mais de «produire» une nouvelle expression algébrique, ce qui requiert un point de vue très différent sur l’utilisation du langage algébrique en lien notamment avec le sens de l’égalité, de la lettre, mais aussi et surtout sur les relations entre les différents symboles (Vlassis, 2010).

Cette expérimentation de l'activité «Antoine fait des mosaïques» apporte également des éclairages sur les conditions favorisant le développement de la généralisation algébrique chez des élèves avant ou au début de l’enseignement de l'algèbre. La phase de mise en commun des différentes formules produites jouera un rôle important dans la progression vers la généralisation algébrique symbolique, dans la mesure où les élèves seront confrontés à l’expression de différent(e)s moyens/formules pour généraliser un processus basé sur un même motif (pattern) figuratif.

L’entrée par le matériel pourrait paraître inadéquate puisque certains élèves éprouvent d’importantes difficultés à s’en détacher, mais cette entrée a permis aux élèves de donner sens à l’expression des opérations et de la généralité. Les élèves peuvent ainsi non seulement baser leur raisonnement sur des actions concrètes, mais également revenir en arrière pour vérifier la production de l’expression finale de la généralité ou encore pour recourir aux premières actions si le sens de l’expression produite vient à manquer.

Et c’est bien là que réside tout l’intérêt de cette séquence construite selon notre modèle, car celui-ci permet de mettre en perspective le processus même d’émergence de la généralité (Dörfler, 1991) en étroite relation avec la symbolisation structurée en chaîne de significations, autorisant ainsi des actions et des opérations sur la base d’un va-et-vient entre le matériel, les nombres, les mots et le langage algébrique. Selon Bednarz (2005), cette capacité à utiliser différents niveaux de langage, à passer d’un niveau de langage à un autre, constitue une habileté centrale en mathématiques, dans la mesure où celle-ci permet de construire un sens aux concepts, aux raisonnements en relation avec le symbolisme mathématique.

Enfin, l’activité, malgré un potentiel qui autorise un développement progressif de la pensée algébrique, ne peut se passer d’un support important de l’enseignant pour étayer la réflexion des élèves ou faire émerger «les mathématiques» des discussions, que ce soient en intervenant dans les groupes ou en organisant une mise en commun qui visera à faire émerger les concepts et les symbolisations relatifs à la pensée algébrique en fonction du niveau scolaire des élèves.

Résumé

Abstract

Resumen

1. Introduction