Article body

Introduction

Quel que soit le contexte, développer une épreuve évaluative demande temps, argent et une variété d’expertises. Autant un enseignant soucieux de la qualité des examens qu’il soumet à ses élèves qu’une firme de testing dont une des activités principales est de développer des items et d’assembler des tests doivent mobiliser des ressources multiples afin d’assurer la qualité du matériel élaboré, et ce, même si leurs intentions et les enjeux diffèrent. Cet article présente les résultats d’une étude visant à mettre en place et à documenter une démarche de développement d’une épreuve diagnostique en mathématique adaptée aux élèves de la formation professionnelle au Québec.

Problématique

La visée diagnostique de l’évaluation est au coeur des préoccupations de nombreux systèmes éducatifs. Plusieurs pays européens évaluent les élèves dans une perspective diagnostique par l’intermédiaire d’épreuves dites externes, c’est-à-dire « conduites par des groupes extérieurs » à l’école, telles que définies par Marcoux et ses collègues (2014, p. 119), systématiques à certains niveaux de la scolarité et sous la responsabilité des divers ministères. Aux États-Unis, ce même courant s’observe, même si la responsabilité du développement des tests incombe souvent à des firmes privées.

Au Québec, il n’existe pas encore de telles démarches à grande échelle. Toutefois, des évaluations diagnostiques se développent à l’interne, à l’initiative d’enseignants dans leur classe ou de conseillers pédagogiques dans leur école. Les difficultés récurrentes vécues par les élèves dans certaines disciplines pointent néanmoins vers un besoin de diagnostic plus systématique (Loye & Lambert-Chan, 2012). C’est notamment le cas en mathématique dans la formation professionnelle (FP). En effet, une variété de programmes de FP reposent sur des savoirs et des compétences en mathématique (Ministère de l’Éducation et de l’Enseignement supérieur [MELS], 2007), par exemple les programmes préparant aux métiers de la construction ou de la santé.

Les conditions d’admission dans ces programmes varient. Elles reposent parfois sur des examens d’admission incluant une épreuve en mathématique et nécessitent en général d’avoir réussi une 4e ou parfois une 3e secondaire. Toutefois, dans les faits, le constat est que beaucoup d’élèves éprouvent de grandes difficultés en mathématique, notamment avec des contenus de base vus au primaire ou au tout début du secondaire (Loye & Barroso da Costa, 2013).

La nature hétérogène de la clientèle actuelle de ces centres de formation, le nombre croissant d’élèves ayant des besoins particuliers (Collectif de recherche sur la formation professionnelle [CRFP], 2009) et le fait que 30 % de ces élèves n’obtiennent pas leur diplôme (MELS, 2010) nous ont donc amenées à cibler ce contexte pour expérimenter une démarche d’élaboration d’épreuves ayant un pouvoir diagnostique. Ces dernières, une fois validées, pourraient à terme faire l’objet d’une passation par les élèves à l’entrée ou avant l’entrée dans un programme de FP et être gérées à l’externe, par exemple par un organisme indépendant des centres de formation, pour éviter d’alourdir la tâche des enseignants. Ce type d’épreuve n’a pas pour vocation de se substituer à des épreuves de sélection dans les programmes, mais plutôt de permettre l’accompagnement des élèves admis de manière plus efficace, à partir d’un diagnostic des forces et difficultés de chacun.

Une telle démarche doit reposer sur une conception précise de la visée diagnostique de l’évaluation dans une approche à grande échelle. L’objet de ce qui suit est de proposer un cadre de référence dans lequel ancrer notre démarche.

Cadre de référence

Une conception de l’évaluation diagnostique

De manière générale, l’évaluation diagnostique vise à mettre en évidence des éléments endogènes ou parfois exogènes à l’individu, puis à déterminer ceux qui posent problème, pour ensuite guider une intervention efficace. La réaliser nécessite donc de passer par deux grandes étapes, dont l’Étape 1 est de définir a priori les éléments sur lesquels faire porter le diagnostic et l’Étape 2, de proposer une méthode pour les mettre en évidence et déterminer ceux qui sont problématiques. Évidemment, la détermination de ces éléments problématiques doit être suivie par la planification d’interventions, dont nous ne traiterons pas ici, mais qui est indispensable une fois le diagnostic posé.

Ketterlin-Geller et Yovanoff (2009) définissent trois approches pour réaliser un diagnostic en mathématique. La première correspond à un calcul des fréquences de bonnes ou mauvaises réponses dans des regroupements d’items visant, par exemple, une même partie du curriculum, telle que l’algèbre ou encore la géométrie, sous forme d’un sous-score. Cette perspective est d’ailleurs celle retenue dans la francophonie, où les résultats des épreuves diagnostiques externes prennent la forme de fréquences de réussites ou d’erreurs, accompagnées de pistes pédagogiques (Marcoux et al., 2014). Toutefois, ces dernières nous semblent ne pas pouvoir être vraiment utiles, étant donné la nature générale du diagnostic proposé.

La seconde approche consiste à analyser les erreurs commises, par exemple à partir d’items dont les choix de réponse correspondent à des erreurs ciblées. Les travaux de Grugeon, en France, reposent sur une analyse didactique et épistémologique des items à partir de leur seule formulation. Ils s’inscrivent dans cette approche, à laquelle est ajoutée une automatisation informatisée de l’analyse des erreurs à partir de choix de réponse erronés et préalablement étiquetés (Grugeon-Allys et al., 2011 ; Grugeon, 2015). Le diagnostic prend alors la forme d’un schéma des erreurs, incluant une recherche de cohérences de fonctionnement, qui nous semble efficace pour guider une planification d’intervention (voir p. ex. Pilet, 2015).

La dernière approche, que nous nommerons approche diagnostique cognitive, est celle qui nous intéresse. À l’instar de Ketterlin-Geller et Yovanoff (2009), nous pensons qu’elle est la plus propice à maximiser le potentiel d’apprentissage de tous les élèves. Elle vise à déterminer les méconceptions persistantes des élèves dans une approche multidimensionnelle. Ancrée à la fois dans la psychologie cognitive et la psychométrie, elle repose sur des items pour lesquels des attributs sous-jacents et à diagnostiquer sont déterminés a priori, et sur des modélisations psychométriques plus complexes, mais potentiellement plus efficaces que de simples calculs de fréquences, sur lesquels s’appuient les deux autres approches.

La modélisation psychométrique des données

L’apparition dans les années 1990 et l’évolution rapide des modèles de classification diagnostique (aussi appelés modèles de diagnostic cognitif ; Loye, 2010 ; Rupp, Templin & Henson, 2010) offrent aujourd’hui un cadre de référence précis et opérationnel pour réaliser des évaluations diagnostiques à grande échelle. Il existe une variété de modèles : ceux-ci sont probabilistes, confirmatoires, à classes latentes et basés sur une structure plus ou moins complexe rendue opérationnelle par l’intermédiaire d’une matrice Q qui fait le lien entre les attributs et les items.

L’utilisation de ces modèles pour traiter les données est en parfaite adéquation avec les deux étapes proposées ci-dessus et avec un contexte de passation à grande échelle. En effet, le diagnostic issu de ces modélisations dépend de deux hypothèses : 1) il est possible de dresser une liste d’attributs portant sur les items du test et 2) de la maîtrise de ces attributs dépend la probabilité de répondre correctement aux items du test. La modélisation nécessite en outre un nombre important de candidats, étant donné la complexité des modèles et le mode d’estimation des paramètres (Rupp et al., 2010). Ils offrent donc la possibilité de produire du feedback multidimensionnel, tout en gardant un temps de test assez court (Bradshaw, Izsák, Templin & Jacobson, 2014).

Ainsi, l’Étape 1 nécessite de déterminer les attributs sur lesquels réaliser le diagnostic dans une intention diagnostique. Ils correspondent à des éléments endogènes ou exogènes, objets du diagnostic. De la cartographie des attributs nécessaires à la bonne résolution de chaque item, formalisée dans la matrice Q, dépend ensuite l’estimation de la probabilité de maîtriser chaque attribut par chaque candidat (voir p. ex. Loye, 2005), ce qui correspond à l’Étape 2. Même si ces modèles font l’objet de très nombreuses études à partir de données simulées, leur application à des données réelles est de plus en plus fréquente. En témoignent par exemple les travaux récents de Jang (2009) et de Rocher (2013) en lecture, ou de Loye (2008), Tjoe et de la Torre (2013a, 2013b) et Bradshaw et ses collègues (2014) en mathématique. Toutefois, à l’exception des travaux actuels du professeur de la Torre et de son équipe, développés en parallèle aux nôtres, peu d’études permettent de vraiment comprendre comment déterminer les attributs, les combiner et construire les items correspondant à ces combinaisons pour obtenir une épreuve en mathématique ayant le pouvoir diagnostique espéré.

La nature des attributs

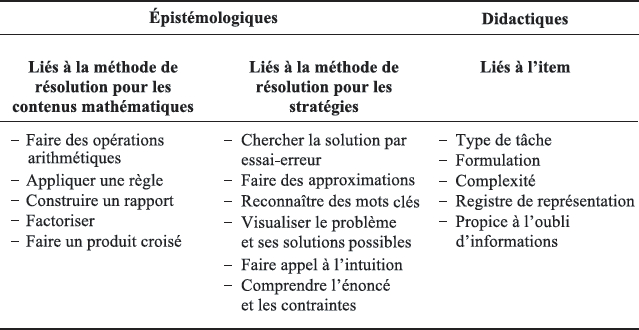
La littérature propose de nombreux exemples d’attributs à utiliser en mathématique dans une perspective de diagnostic cognitif. Toutefois, ces modèles ne reposent pas sur une théorie de la cognition. C’est d’ailleurs la raison pour laquelle nous préférons l’appellation de classification diagnostique à celle de diagnostic cognitif. Les auteurs souhaitant faire le lien entre des items et des attributs commencent en général par en proposer une synthèse (voir p. ex. Bradshaw et al., 2014 ; Loye, 2008 ; Tjoe & de la Torre, 2013b). De manière générale, ces attributs, parfois aussi appelés compétences de base, sont directement issus du domaine mathématique et font référence à des contenus ou des stratégies, ce qui s’inscrit dans l’approche épistémologique telle qu’elle est définie par Grugeon (2015). D’autres sont endogènes, autrement dit liés à l’item et non à l’élève, et vus comme une conséquence de variables didactiques (Grugeon, 2015). Le tableau 1 en propose quelques exemples.

Tableau 1

Quelques exemples d’attributs épistémologiques et didactiques

Quelques exemples d’attributs épistémologiques et didactiques

-> See the list of tables

Plusieurs études pointent vers le peu de pouvoir diagnostique des tests lorsque les modélisations se basent sur des attributs déterminés a posteriori et sur des données issues d’épreuves non conçues dans cette perspective (Bradshaw et al., 2014 ; Gorin, 2007 ; Leighton & Gierl, 2007 ; Loye et al., 2011). Ainsi, relever le défi de produire une épreuve ayant un réel potentiel diagnostique est l’objectif de notre étude.

Objectif de l’étude

La méthode proposée par Downing et Haladyna (2006) nous apparaît comme systématique et exhaustive en ce qui concerne le design de tests. Dans notre contexte, documenter la mise en oeuvre de l’Étape 1 correspond à ce que proposent ces auteurs entre la planification générale et l’assemblage du test. Ainsi, élaborer une démarche empiriquement soutenue pour définir les attributs à diagnostiquer chez les élèves de la FP en mathématique nécessite 1) de réaliser une planification générale, 2) de définir les contenus visés, 3) de définir les spécifications du test, 4) de développer les items, et 5) d’assembler le test. Cela nécessite aussi de tenir compte de notre cadre de référence lié à une visée diagnostique, et de déterminer les attributs et leurs liens avec les items conformément à une perspective de modélisation, à l’aide de modèles de classification diagnostique.

Sur la base d’une étude exploratoire auprès des enseignants de la FP (Loye & Barroso da Costa, 2013), nous avons précédemment mis en évidence le besoin de diagnostic relativement au raisonnement logique, à l’application de techniques de calcul, à la compréhension des énoncés et à la résolution nécessitant plusieurs étapes, notamment dans des problèmes liés à l’utilisation des fractions et des proportions. Nous avons également retenu l’importance d’utiliser des items ancrés dans la réalité professionnelle des élèves du Québec, celle-ci impliquant entre autres le recours à deux systèmes de mesure, l’un métrique et l’autre impérial[1].

Ainsi, la présente étude vise à documenter le processus d’élaboration d’items portant sur les fractions et les proportions, sur la mise en évidence des attributs qui leur sont sous-jacents et sur l’assemblage de ces items en une épreuve structurée par une matrice Q. Nous avons retenu les programmes de formation du domaine de la construction, étant donné le nombre important d’élèves inscrits dans ces programmes dans les divers centres de la grande région de Montréal, ce qui nous offre un bassin de grande taille pour nos expérimentations. L’objectif est d’assembler une épreuve ayant un potentiel diagnostique compatible avec la modélisation des données à l’aide d’un modèle psychométrique de classification diagnostique, puis de laisser des traces de la démarche afin de pouvoir la reproduire ensuite pour d’autres contenus mathématiques, programmes et disciplines.

Une fois défini le choix de contenus mathématiques portant sur les fractions et les proportions, et une fois ciblé le contexte de la FP dans le domaine de la construction, nous avons réalisé une planification générale et défini les contenus visés (étapes 1 et 2 de la démarche de Downing & Haladyna, 2006). Il convenait alors de déterminer quels acteurs devaient prendre part à la démarche. Nous avons choisi de faire appel à des experts de contenu, qu’ils soient enseignants ou didacticiens, pour écrire des items, tout en tentant en parallèle de définir les attributs à diagnostiquer ; puis à des élèves pour mettre les items à l’essai et stabiliser les attributs sous-jacents à chaque item. Le choix d’utiliser des items à correction objective a en outre été dicté par la nécessité d’une correction rapide conforme à nos besoins dans le cadre d’une évaluation à grande échelle et d’une gestion d’épreuve à l’externe.

Cet article présente les trois phases qui ont été nécessaires à l’assemblage d’une épreuve en mathématique à faire passer à grande échelle dans les centres de FP offrant des programmes en construction.

Phase 1

La méthodologie de la Phase 1

Étant donné le peu d’exemples de mode de développement d’une telle épreuve disponibles dans la littérature, la Phase 1 a été très exploratoire. Elle visait essentiellement à mettre en évidence les attributs et à faire émerger une intention diagnostique. À l’automne 2012, une enseignante de mathématique du secondaire habituée à produire des items dans une visée de sélection a été recrutée et mise au courant du projet. Elle a produit 9 items à réponse choisie conformes à nos attentes de contenu ciblé et de clientèle visée. Toutefois, une réelle réflexion sur les attributs à diagnostiquer avec ces items ne lui a pas été possible à partir des informations que nous lui avions fournies et qui devaient contribuer à définir les spécifications du test (étape 3 de la démarche de Downing & Haladyna, 2006). En fait, sa proposition d’étiquetage des items se limitait au domaine mathématique visé, soit les pourcentages ou les fractions.

À la suite du regard critique de deux élèves du collégial chargés de résoudre les items et de les commenter, nous avons retenu 8 de ces items et mis en place une passation d’une durée de 2 heures, dans une classe de 13 élèves, lors de leur première semaine de formation en charpenterie.

À l’instar de Roberts et ses collègues (2012) et de Tjoe et de la Torre (2013a), nous avons choisi un protocole de verbalisation à haute voix (Ericsson & Simon, 1993) afin de recueillir des données portant sur le mode opératoire des élèves pour répondre à ces items. Un cahier contenant les énoncés des 8 items leur a été fourni en version papier avec pour consigne de résoudre les questions par écrit dans le cahier, tout en verbalisant à haute voix toute leur démarche, depuis la lecture de l’énoncé jusqu’au choix d’une réponse parmi celles proposées pour chaque item. Les données ont donc été constituées par l’ensemble des cahiers remplis par les élèves et des enregistrements audios individuels, qui ont ensuite été retranscrits en verbatims.

La correction et les analyses par une didacticienne en mathématique ont permis de produire 104 cartes conceptuelles illustratives de la démarche utilisée par chaque élève pour chaque item, incluant les erreurs commises. (Un exemple de carte est disponible à la figure 1 p. 40.)

Les résultats de la Phase 1 et discussion

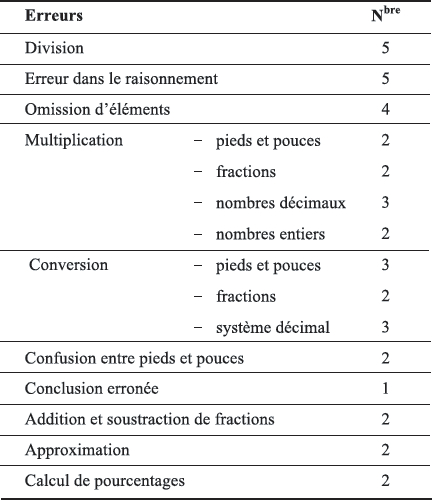
Les résultats de la Phase 1 ont d’abord confirmé la difficulté de produire des items dans une visée diagnostique, tout en définissant en parallèle les attributs qu’ils permettront de diagnostiquer. Ils ont également permis de mettre au point un mode d’analyse efficace des données recueillies dans les protocoles de verbalisation à haute voix par la création de cartes conceptuelles. Une synthèse grossière des cartes par item a ensuite été réalisée par classification dans le but de faire émerger les différentes démarches possibles pour résoudre un même item et pour tenter de dégager des attributs. Ainsi, nous avons constaté que peu d’items donnaient lieu à un mode de résolution unique, mais nous avons réussi à mettre en évidence des erreurs types et récurrentes (voir Tableau 2). En outre, les discussions informelles avec les élèves à la suite de la collecte de données nous ont amenées à comprendre le manque de plausibilité du contexte proposé dans l’un des items. Même si ces premiers résultats semblaient nous éloigner de l’approche diagnostique cognitive que nous avions retenue et nous informaient peu sur la manière de stabiliser une intention diagnostique, ils ont servi de base à la Phase 2.

En nous appuyant sur les démarches et les erreurs commises, nous avons recommencé à produire des items. Notre intention était de parvenir cette fois à cibler les processus au moment de leur élaboration afin de faire enfin émerger les attributs à diagnostiquer.

Tableau 2

Nombre d’erreurs commises par les élèves à la Phase 1

Nombre d’erreurs commises par les élèves à la Phase 1

-> See the list of tables

Phase 2

La méthodologie de la Phase 2

Dans la Phase 2, nous avons sollicité deux didacticiennes, incluant celle ayant produit les cartes conceptuelles de la Phase 1, pour écrire un nouvel ensemble d’items. Chaque item a été étiqueté selon les contenus mathématiques requis en s’inspirant des démarches correctes et erronées mises en évidence dans la Phase 1. Voici des exemples de ces étiquettes : aire ; conversion entre pieds et pouces ; conversion entre mètres et centimètres ; conversion entre mètres carrés et centimètres carrés ; division avec des nombres entiers ; division avec des fractions ; division avec des nombres décimaux ; multiplication avec des nombres entiers ; etc. Nous avons ainsi disposé d’un total de 25 nouveaux items inscrits dans le domaine de la construction, mais aussi dans le domaine de la santé et d’autres plus généraux.

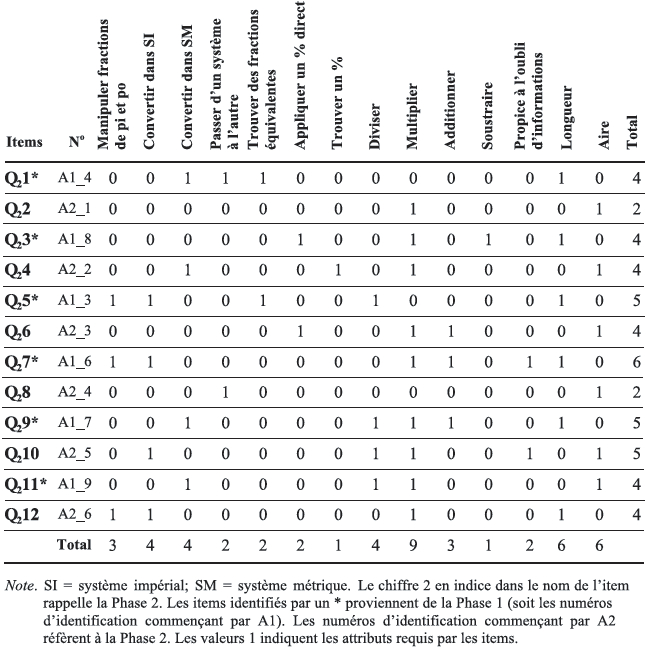
Nous avons ensuite retenu 6 items du domaine de la construction et les avons combinés à 6 items expérimentés dans la Phase 1. Nous avons en outre établi une structure a priori de l’épreuve ainsi construite. Pour les items issus de la Phase 1, nous avons porté un jugement qualitatif sur les démarches et erreurs observées. Pour les nouveaux items, nous avons utilisé l’étiquetage. Cette structure a priori, qui évoluera à la lumière des données recueillies et analysées après passation par des élèves, fait l’objet du tableau 3 et correspond à une ébauche de matrice Q pour cette épreuve ; elle comporte 14 attributs reliés à 12 items. Tous les items sont à réponse choisie parmi 4 à 6 choix, sauf l’item 12, qui demande une réponse courte. Les attributs retenus sont tous de nature épistémologique, à l’exception de « Propice à l’oubli d’informations » lié à l’item. Notons que l’attribut « Passer d’un système à l’autre » pourrait être vu comme étant didactique en référence aux registres de représentation.

Tableau 3

Matrice Q établie a priori dans la Phase 2

Matrice Q établie a priori dans la Phase 2

-> See the list of tables

L’objectif de la Phase 2 était de mettre cette structure à l’épreuve en comparant les résolutions d’élèves à ce qui était attendu, selon un protocole identique à celui de la Phase 1. À l’automne 2014, nous avons procédé à des passations dans trois programmes de formation et retenu les données de 25 élèves (voir Tableau 4) sur la base de la qualité du document audio et des traces laissées dans le cahier de réponses, indépendamment du fait d’obtenir ou pas les bonnes réponses aux items. En outre, à la suite des passations des groupes 1 et 2 et des premières analyses, nous avons constaté que le fait de ne pas avoir accès à une calculatrice amenait de nombreux élèves à rester bloqués sur les calculs, à ne pas avancer dans le raisonnement et à finalement ne fournir aucune réponse. Ce constat est cohérent avec l’usage qui est fait de la calculatrice dans la formation de certains élèves, par exemple sa place très importante dans la formation des adultes dès les apprentissages de base. C’est la raison pour laquelle nous avons autorisé les élèves du groupe 3 à utiliser leur calculatrice. Le pourcentage d’items sans réponse a ainsi beaucoup diminué dans le groupe 3.

Tableau 4

Participants de la Phase 2

Participants de la Phase 2

-> See the list of tables

Les données de la Phase 2 ont donc été constituées par l’ensemble des cahiers remplis par les 25 élèves et des enregistrements audios individuels, qui ont ensuite été retranscrits en verbatims.

Figure 1

Exemple de carte conceptuelle et du codage correspondant. La couleur grise est utilisée lorsque le processus conduit à une erreur et lorsque la réponse est fausse.

-> See the list of figures

La correction et les analyses par une didacticienne en mathématique ont permis de produire 300 cartes conceptuelles illustratives de la démarche utilisée par chaque élève pour chaque item, incluant les erreurs commises. Nous avons ensuite analysé de manière qualitative et systématique chacune des cartes en codant chacun des noeuds et en précisant si le résultat obtenu était correct ou incorrect, à chaque étape et globalement. La figure 1 propose un exemple de carte et du codage réalisé. Les allers et retours entre les verbatims, les cahiers et les cartes ont assuré la validité du codage. Cette approche a permis de constituer une base de données Excel regroupant tous les processus utilisés par item ainsi que par élève. Les résultats présentés dans la section qui suit correspondent aux analyses descriptives de ces données réalisées à l’aide d’Excel et du logiciel pour analyse statistique SPSS.

Les résultats de la Phase 2

La mise à jour des attributs

Le codage des données a fait émerger trois nouveaux attributs, qui sont : « Faire un produit croisé », « Utiliser une approximation » et « Passer d’une fraction à un nombre décimal ». En ce qui concerne l’approximation, elle a été très utilisée par les élèves des groupes 1 et 2 qui, privés de calculatrice, ont tenté de contourner les opérations par cette stratégie. Toutefois, nous avons noté que quelques élèves qui disposaient d’une calculatrice y ont également eu recours (voir Tableau 5). De plus, nous n’avions pas envisagé le passage d’une écriture fractionnaire à une écriture décimale, avec ou sans approximation, stratégie pourtant beaucoup utilisée par les élèves et que l’usage de la calculatrice semble favoriser. Le fait de le voir comme une stratégie des élèves plutôt que comme une caractéristique de l’item nous a amenées à classer cet attribut comme épistémologique.

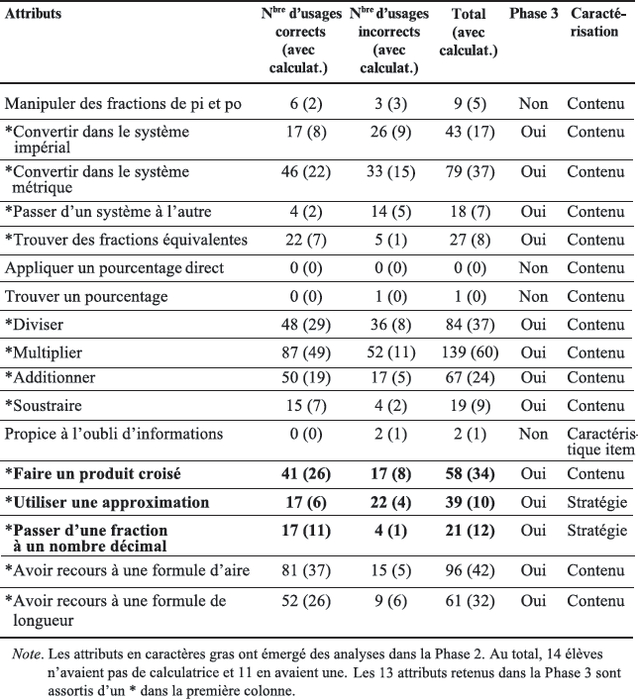
Ainsi, à part l’attribut « Faire un produit croisé » qui correspond à un contenu mathématique, les attributs émergents sont plutôt de l’ordre des stratégies. Certains des attributs attendus ont également été peu observés, comme en témoigne le tableau 5, qui récapitule les nombres d’usages corrects et incorrects. C’est le cas de l’attribut didactique « Propice à l’oubli d’informations », qui n’a mené finalement qu’à deux erreurs portant sur les items 5 et 9 – et non sur les items 7 et 10 selon nos attentes – et qui a été abandonné. L’attribut « Manipuler des fractions de pieds et de pouces » a peu émergé, en comparaison de « Convertir dans le système impérial ». Nous avons donc décidé de les regrouper sous l’attribut « Convertir dans le système impérial ». Finalement, « Appliquer un pourcentage direct » et « Trouver un pourcentage » ont été déclinés de manière plus précise dans les quatre attributs d’opération ou dans le nouvel attribut « Faire un produit croisé », et ont finalement peu été observés et eux aussi abandonnés. Pour la Phase 3, nous avons donc décidé de ne garder que les 13 attributs définis comme tels dans le tableau 5.

Tableau 5

Utilisation des attributs dans la Phase 2

Utilisation des attributs dans la Phase 2

-> See the list of tables

La comparaison entre les attributs attendus et les attributs utilisés

Nous avons également comparé les attributs attendus (selon le tableau 3) et les attributs utilisés par les élèves. Pour avoir une vue d’ensemble relativement à chaque item, nous avons calculé la corrélation bisériale de point entre le nombre total de fois que les attributs ont été sollicités (variable continue), qu’ils le soient avec succès ou non, et le fait que les attributs soient attendus ou non pour l’item (variable dichotomique). Les résultats se trouvent dans la colonne 3 du tableau 6. Dans l’ensemble, les corrélations sont fortes et statistiquement significatives, et ce, même avec trois nouveaux attributs. Il n’y a que pour les items 1 et 12 que les démarches des élèves s’éloignent de ce qui avait été prévu, sans que nous ayons d’explication précise.

L’analyse des items

Une rapide analyse d’items, ancrée dans la théorie classique des tests (TCT) étant donné le petit nombre d’élèves, a été réalisée avec le logiciel jMetrik sur les 11 items à réponse choisie (a = 0,7743). Nous y avons ajouté une analyse non paramétrique du fonctionnement des choix de réponse en fonction du score total obtenu (1 point par bonne réponse et 0 point sinon).

La synthèse des résultats se trouve dans le tableau 6. À l’issue de ces analyses, nous avons retiré deux items jugés problématiques selon leur discrimination ou le fonctionnement des choix de réponse. Nous avons ramené le nombre de choix de réponse à quatre pour les items à réutiliser dans la Phase 3. Ceux-ci sont de difficultés variables.

Une matrice Q améliorée

Nous avons ainsi retravaillé la matrice Q pour les 10 items retenus et considéré qu’un lien existe entre l’attribut et l’item lorsqu’il a été observé au moins trois fois au total. Cette matrice fait l’objet du tableau 7. Selon cette matrice, chaque item nécessite un nombre d’attributs variant de 2 à 8 ; l’attribut « Passer d’un système à l’autre » ne correspond qu’à l’item 8, tandis que « Multiplier » est requis pas tous les items, sauf un. Cette matrice pose les bases pour définir les spécifications du test (étape 3 de la démarche de Downing & Haladyna, 2006).

Tableau 6

Synthèse des résultats de l’analyse des items

Synthèse des résultats de l’analyse des items

-> See the list of tables

Tableau 7

Matrice Q à l’issue de la Phase 2 pour les 10 items retenus

Matrice Q à l’issue de la Phase 2 pour les 10 items retenus

-> See the list of tables

Une tentative de diagnostic

L’utilisation de l’approche diagnostique cognitive repose sur l’hypothèse selon laquelle la réussite des items dépend du niveau de maîtrise des attributs sous-jacents. Notre mode de collecte de données nous a permis de déterminer un par un les attributs mis en oeuvre, correctement ou pas, par chaque élève dans la résolution de chaque item. Ainsi, le caractère redondant des erreurs concernant un même attribut nous fournit une information diagnostique. Pour 21 élèves, il est ainsi possible de mettre en évidence des méconceptions par le caractère répétitif des attributs occasionnant une erreur. De manière logique, pour les deux élèves ayant obtenu les meilleurs scores (respectivement 9/12 et 10/12), il n’y a pas d’attribut fautif de manière répétitive. Enfin, seuls deux élèves avec un score moyen (6/12 et 7/12) ont des erreurs liées à une variété d’attributs sans répétitions. Ainsi, ces résultats nous semblent compatibles avec notre hypothèse.

Nous avons noté que trois élèves n’ont obtenu aucune bonne réponse, tandis que trois autres n’ont obtenu qu’une seule bonne réponse. Notre mode de collecte nous a toutefois permis d’observer leur bon usage de certains attributs. Dans une collecte à grande échelle, il serait évidemment impossible de procéder ainsi. L’approche diagnostique cognitive que nous avons retenue se base sur les bonnes et mauvaises réponses aux items et nous n’aurions pas la possibilité d’établir un diagnostic pour des élèves qui ne proposent aucune bonne réponse. Ce point attire notre attention sur la nécessité d’intégrer des items plus faciles à notre épreuve, par exemple des items ne faisant appel qu’à un seul attribut, pour nous assurer d’obtenir un certain nombre de bonnes réponses de la part des candidats les plus faibles.

Afin de tenter de comparer notre approche empirique à une approche cognitive pour notre échantillon, nous avons mis en lien les mauvais usages observés des attributs avec les mauvais usages supposés des attributs à partir des bonnes et mauvaises réponses des élèves aux 12 items. L’indicateur alors utilisé était le rapport du nombre d’items faux sur le nombre total d’items recourant à un même attribut. La corrélation[2] (r = 0,233 ; p < 0,001) entre les deux valeurs (nombre de mauvais usages et indicateur) nous offre un certain regard sur le potentiel diagnostique de nos items selon la matrice Q. Même si cette corrélation est assez faible, elle indique une certaine concordance entre les deux regards portés.

La discussion issue de la Phase 2

Les résultats de la Phase 2 nous ont amenées à certains constats pour guider la Phase 3. L’objectif en est l’assemblage d’une épreuve qui pourra faire l’objet d’une passation à grande échelle et d’une modélisation des données à l’aide d’un modèle de classification diagnostique. Tout d’abord, nous estimons que la redondance des attributs problématiques observés chez la plupart des élèves nous montre que les items que nous développons respectent les hypothèses sur lesquelles repose l’approche diagnostique cognitive retenue.

De plus, nous avons stabilisé une structure pour la matrice Q en proposant une liste d’attributs de nature épistémologique qui cadrent notre intention diagnostique, puis en retenant 10 items qui s’y inscrivent. Nous jugeons que les corrélations élevées entre les attributs attendus et utilisés témoignent de la valeur du mode opératoire développé dans la Phase 2, qui est donc à réutiliser dans la Phase 3 pour compléter notre liste d’items. Nous avons aussi constaté la difficulté à produire des items inscrits dans le domaine de la construction sans recourir à des experts de ce domaine.

En outre, il existe un actuel déséquilibre dans la matrice Q que nous avons produite. Même si la majorité des attributs se distribuent assez bien entre les items, l’usage de certains d’entre eux nécessite de produire de nouveaux items. C’est le cas de l’attribut « Passer d’un système à l’autre », qui ne correspond qu’à un seul item (voir Tableau 7). Nous devons donc développer des items portant spécifiquement sur cet attribut ou l’abandonner.

A contrario, la quasi-totalité de nos items nécessite le recours à une multiplication (voir Tableau 7). Étant donné les grandes difficultés de plusieurs élèves à l’égard des calculs et les stratégies d’évitement qu’ils mettent en oeuvre, ce diagnostic, comme celui lié à toutes les opérations, est essentiel. Nous avons observé que leur incapacité à faire le calcul amène plusieurs élèves à ne pas apporter une réponse à la question. Étant donné que notre épreuve doit permettre de mettre en évidence les problèmes liés aux calculs, mais qu’elle ne doit pas s’y limiter, nous avons décidé de contrôler le nombre d’items reliés aux attributs de type calcul en permettant l’usage de la calculatrice pour les items nécessitant des calculs un peu longs ou complexes.

Enfin, nous constatons que le nombre d’attributs retenus est grand et posera à l’évidence des problèmes au moment de la modélisation des données, si nous voulons assembler une épreuve dont la passation ne dépasse pas 1 heure à 1 heure et demie. Toutefois, nous aviserons des manières de disposer des attributs et de gérer leur nombre lorsque nous en serons à modéliser des données. Nous notons également qu’aucun attribut didactique n’a été retenu et que des items faciles sont nécessaires pour minimiser le nombre de scores nuls à l’issue de la passation.

Pour résumer, à l’issue de la Phase 2, nous avons 1) réalisé une planification générale, 2) défini les contenus visés, 3) défini les spécifications du test, et 4) développé quelques items (étapes 1 à 4 de la démarche de Downing & Haladyna, 2006). La Phase 3 doit consister à développer des items de manière à assembler un test (étape 5 de la démarche) conforme aux spécifications que nous avons retenues en tirant profit des constats réalisés dans les phases précédentes.

Phase 3

La méthodologie de la Phase 3

La Phase 3 débute avec le travail de développement de nouveaux items par les deux enseignants des groupes 2 et 3 de la Phase 2. Le regard critique qu’ils portaient sur les items et leur intérêt pour le projet les a amenés à ainsi y apporter leur contribution. À partir des attributs mis en évidence dans la Phase 2 et des items disponibles servant de modèles, ils ont produit 20 nouveaux items et les ont étiquetés avec les attributs disponibles. Même si l’exercice de production d’items reste difficile, nous avons constaté que le fait de leur fournir les attributs les guidait efficacement, comparativement à ce que nous avions proposé à l’enseignante de la Phase 1. Nous avons aussi constaté que des enseignants du domaine étaient plus à même de proposer des contextes plausibles et réalistes, ce qui avait posé problème dans les deux premières phases.

Dans la perspective d’élaborer une première version d’épreuve de 20 items pour limiter le temps de passation, nous avons sélectionné 10 de ces nouveaux items et les avons combinés aux 10 items retenus à l’issue de la Phase 2.

Nos contraintes de choix étaient dictées par les constats réalisés dans la Phase 2. Nous devions ajouter des items jugés plus faciles et propices à être résolus sans le recours à une calculatrice. Nous devions en outre ajouter au moins un item portant sur l’attribut A3 « Passer d’un système à l’autre ». De plus, nous devions prendre en compte la complexité des problèmes proposés pour limiter la difficulté anticipée des items et le temps nécessaire à leur résolution. Enfin, des critères comme la clarté de la formulation ou la longueur des énoncés ont également été pris en compte. Nous avons ainsi retenu 6 nouveaux items pour la partie de l’épreuve à passer sans calculatrice et 4 pour la partie dans laquelle la calculatrice est permise.

Pour ces 10 nouveaux items, une enseignante habituée à produire des items dans une perspective de sélection a revu le contenu, les choix de réponse et la formulation. Elle a également proposé des corrections pour les choix des réponses des 10 items de la Phase 2, conformément aux commentaires issus des analyses et présentés dans la dernière colonne du tableau 6. Son travail de révision a permis de stabiliser les énoncés des 20 items de l’épreuve ainsi construite, dont la structure fait l’objet du tableau 8. Ce dernier correspond à la matrice Q construite a priori en même temps que l’épreuve et qui servira de base aux modélisations, à l’aide d’un modèle de classification diagnostique, lorsque des données auront été recueillies en quantité suffisante. Le travail de la Phase 3 a ainsi permis de continuer à développer les items et à assembler l’épreuve (étapes 4 et 5 de la démarche de Downing & Haladyna, 2006).

Les résultats de la Phase 3 et discussion

Le tableau 8 met en évidence les choix que nous avons faits pour équilibrer la matrice Q. L’ajout de l’attribut A0 « Utiliser la calculatrice » a permis de limiter le nombre d’items reliés à chacune des opérations. Ainsi, même si nous avons déterminé les opérations nécessaires à tous les items, nous n’établirons un lien avec les opérations que pour les items pour lesquels la calculatrice n’est pas permise lorsque nous modéliserons les données. Les items sont reliés à un nombre d’attributs variant de 1 à 6. En outre, chaque attribut est requis par un nombre d’items allant de 3 à 12. Madison et Bradshaw (2015) suggèrent de proposer autant que possible au moins un item relié de manière isolée à chaque attribut, ce qui est cohérent avec notre constat d’un besoin d’items plus faciles, potentiellement reliés à un seul attribut. La contrainte est alors d’allonger le nombre d’items et, donc, le temps de passation, ce qui est difficile dans notre contexte. Dans ce cas, ces auteurs recommandent de varier les combinaisons d’attributs, ce que nous avons fait et ce dont témoigne le tableau 8.

Pour le moment, nous avons renoncé à définir les items avec des attributs de nature didactique. Toutefois, il est probable que les modélisations des données nous amèneront à reconsidérer ce choix.

Tableau 8

Synthèse du montage de l’épreuve

Synthèse du montage de l’épreuve

-> See the list of tables

Conclusion et étapes à venir

Les trois phases ont permis de développer une première version d’épreuve. La procédure itérative que nous avons retenue nous a permis de tirer profit de chaque phase pour mettre en place la suivante afin de documenter l’Étape 1 selon notre conception du diagnostic. Cette étude fournit un premier modèle de démarche permettant de stabiliser une intention diagnostique sous la forme d’une liste d’attributs à diagnostiquer et de construire les items nécessaires à son opérationnalisation. Les différentes phases nous ont enseigné la nécessité de recourir à une variété d’acteurs pour mettre en place la démarche et celle de commencer par définir les attributs pour faciliter la production des items. À ce stade, nous avons développé une épreuve de 20 items reposant sur une structure et avons documenté en détail le travail qu’elle a nécessité.

Un retour réflexif sur notre démarche met clairement en évidence sa nature très empirique ; en témoigne d’ailleurs le style narratif de notre article. Les décisions que nous avons prises au fur et à mesure ont été dictées par le terrain et ne prenaient appui ni sur d’autres études ni sur une théorie cognitive qui auraient pu nous guider.

Nous faisons un bilan positif des trois phases réalisées et considérons avoir atteint nos objectifs à ce stade de l’étude. Toutefois, nous sommes aussi conscientes de la nécessité de faire émerger un cadre de référence plus théorique pour soutenir la production future des attributs d’une épreuve diagnostique. L’ensemble du travail réalisé nous amène à chercher à puiser un tel cadre à la didactique des mathématiques, ce qui ne nous semblait pas possible au début de cette étude. Ainsi, nous considérons aujourd’hui que les travaux de Grapin (2015) nous offrent une piste de réflexion quant à un étiquetage des items non pas uniquement lié à la manière de résoudre les items par les élèves – ce qui correspond à notre approche –, mais également lié à ce qui a été enseigné à ces élèves. Cette approche ne sera pas sans poser de problèmes dans notre contexte, étant donné la nature très hétérogène de la population d’élèves que nous visons à évaluer avec l’épreuve développée. Toutefois, une analyse des programmes d’études des secteurs jeunes et adultes pourrait générer un référent complémentaire et utile.

La phase suivante de la recherche consistera en une mise à l’essai auprès d’un groupe d’élèves pour vérifier la formulation des items et leur validité apparente auprès de la clientèle visée. Par la suite, une passation à grande échelle est prévue afin de collecter des données auprès d’environ 500 élèves et de modéliser les données ainsi recueillies. Ces modélisations viseront une variété d’objectifs inscrits dans l’Étape 2, par exemple vérifier le potentiel diagnostique de l’épreuve, étudier la validité du diagnostic obtenu ainsi que déterminer les ajustements nécessaires aux items et à la matrice Q. À l’issue de ces analyses, et probablement de celles sur de nouvelles données obtenues après ajustements sur les items et sur la matrice Q, nous espérons stabiliser une épreuve validée qui pourra alors porter l’appellation de test diagnostique, et dont le potentiel diagnostique sera assuré et documenté.