Abstracts
Résumé
Plusieurs facteurs contribuent à l’instabilité des berges dans les méandres, mais le rôle joué par la dynamique de l’écoulement complexe au sein de ces sites n’est pas clairement élucidé. L’objectif de cette recherche est d’examiner la dynamique de l’écoulement tridimensionnel (3D) d’une boucle de méandre en vue de déterminer les liens entre la structure de l’écoulement moyen et turbulent, la contrainte de cisaillement et l’érosion des berges. Des données de vitesse 3D ont été recueillies dans une boucle de méandre avec un vélocimètre acoustique Doppler (ADV) et un profileur acoustique Doppler conçu pour les rivières peu profondes (PC-ADP). Une comparaison entre ces deux appareils a révélé que le PC-ADP donne de bons estimés de vitesse moyenne dans un écoulement relativement simple (au centre du chenal), mais le problème de moyennage spatial le rend moins efficace dans un plan de mélange où l’écoulement est plus complexe. L’ADV est aussi supérieur au PC-ADP pour les estimés de contrainte de cisaillement et l’étude de la turbulence à petite échelle, mais ce dernier révèle mieux les patrons à grande échelle. Deux cellules d’écoulement secondaire dans le méandre ressortent nettement avec les mesures simultanées du PC-ADP. Les maxima de contrainte de cisaillement mesurée avec l’ADV par la méthode d’énergie turbulente cinétique sont situés à l’entrée du méandre lorsque le niveau est plus bas, et à la sortie du méandre lorsque le niveau augmente. Ces deux zones correspondent à des observations de décrochement de berge au site d’étude.
Abstract
Many factors contribute to bank instability in meanders, but the exact role played by the complex flow dynamics is not very well understood. The objective of this research is to examine the three-dimensional (3D) flow dynamics in a meander loop to determine the links between the mean and turbulent flow structure, and bank erosion. 3D velocity data were collected in a meander loop with an acoustic Doppler velocimeter (ADV) and a pulse-coherent acoustic Doppler profiler (PC-ADP). A comparison between these two devices revealed that the PC-ADP provides accurate estimates of mean velocity in a relatively simple flow (in the centre of the channel), but that it is less efficient in a complex flow field with a mixing zone due to spatial averaging problems. The ADV is also better than the PC-ADP for bed shear stress estimates and for small-scale turbulence studies, but the latter reveals large-scale structures efficiently. Two secondary cells in the meander loop are clearly seen from the simultaneous PC-ADP measurements. The maximum values of bed shear stress measured with the ADV with the turbulent kinetic energy method are located at the meander entrance when flow stage is low, and at the meander exit when flow stage increases. These two zones correspond to observations of bank failure events at the field site.
Article body
Introduction
Bien qu’il s’agisse d’un phénomène naturel, l’érosion des berges liée à la présence de boucles de méandre constitue un problème majeur, particulièrement en milieu agricole. Aux États-Unis par exemple, il a été estimé que près d’un million des 5,6 millions de kilomètres de rivières enregistrent une érosion de berge (Biedenharn et al., 1997). Cette érosion engendre des pertes importantes de terrains publics et privés, une baisse de la qualité de l’eau et une sédimentation accrue des rivières, et peut avoir des impacts économiques et environnementaux sévères (Piégay et al., 2005). Il n’est donc pas surprenant que plusieurs projets de stabilisation des berges aient été implantés. Les méthodes d’ingénierie « dure » utilisent souvent des perrés (riprap) le long de la berge externe, tandis que les méthodes dites douces (soft-engineering), plus écologiques et plus esthétiques (Lee et al., 1997), utilisent la végétation pour accroître la résistance des berges.
Plusieurs études ont été menées afin d’identifier les facteurs responsables de l’instabilité des berges (Darby et Thorne, 1996 ; Allen et al., 1999 ; Simon et Collison, 2001). Ces études tendent à se concentrer sur les mesures de retrait des berges ou sur la mécanique de décrochement, mais elles ne permettent pas de réellement comprendre l’interaction entre la dynamique de l’écoulement et l’érosion de la berge. Des simulations numériques basées sur des modèles empiriques, validées à l’aide de données historiques, ont aussi été réalisées (Jia and Wang, 1999 ; Wu et al., 2000), mais l’échelle d’analyse était celle du bassin versant plutôt que des boucles individuelles de méandre. Les rares tentatives d’appliquer ces résultats à l’échelle d’une section de rivière n’ont pas été validées (Mosselman et al., 2000) ou bien elles ont grandement simplifié les processus, donnant lieu à des résultats discutables (Darby et Delbono, 2002 ; Darby et al., 2002).
La dynamique de l’écoulement dans les méandres est tridimensionnelle (3D) en raison des écoulements secondaires, nommés cellules hélicoïdales, engendrés par la force centrifuge, orientée vers la berge externe, et le gradient de pression lié à l’inclinaison latérale de la surface de l’eau, orienté vers la berge interne. Le développement d’appareils de mesure de vitesse enregistrant simultanément les trois composantes de l’écoulement tels que le vélocimètre acoustique Doppler (ADV) ou le profileur acoustique Doppler (ADCP) a permis une meilleure compréhension de la structure de l’écoulement moyen des méandres au cours des dernières années (Frothingham et Rhoads, 2003 ; Daniels et Rhoads, 2004 ; Dinehart et Burau, 2005 ; Shields et Rigby, 2005). De plus, les modèles de simulation numériques 3D sont maintenant capables de fournir un portrait détaillé des vecteurs moyens de vitesse 3D, même dans des boucles de méandres de cours d’eau naturels ayant une topographie du lit complexe (Ferguson et al., 2003 ; Rodriguez et al., 2004 ; Rüther et Olsen, 2005). Toutefois, aucune étude n’a à notre connaissance fait état de la structure turbulente 3D dans les méandres.
Malgré ces progrès substantiels dans la compréhension de la dynamique moyenne 3D des dernières années, le lien entre l’hydraulique du cours d’eau et la stabilité de la berge est encore confus. Par exemple, Rodriguez et al. (2004) affirment que les vitesses près du lit gouvernent tant l’érosion de la berge externe que le dépôt de sédiments le long de la berge interne, et qu’elles sont utilisées pour calculer les taux de migration dans les modèles d’évolution de la géométrie en plan des méandres (Ikeda et al., 1981 ; Johanesson et Parker, 1989). Il semble toutefois essentiel d’examiner attentivement la zone proximale de la berge, pas nécessairement seulement près du lit, afin de mieux comprendre les processus d’érosion de berge. Dans le même article, Rodriguez et al. (2004) indiquent que l’érosion de la berge dépend du flux de sédiments près de la berge, lui-même associé à la distribution spatiale des vitesses 3D, ce qui semble contredire leur affirmation précédente. Il faudrait aussi déterminer comment quantifier la distribution spatiale des vitesses 3D. Par exemple, faut-il déterminer une contrainte de cisaillement appliquée sur la berge (qui dépendrait alors de la composante latérale de vitesse, en plus de la composante longitudinale), ou doit-on utiliser des méthodes plus traditionnelles d’estimés de contrainte de cisaillement ?
L’objectif de cette recherche est d’examiner la dynamique 3D d’une boucle de méandre. Plus spécifiquement, nous investiguerons la question de la mesure des contraintes de cisaillement en lien avec le problème d’érosion de berges, de même que la structure de l’écoulement moyen et turbulent dans un méandre. Enfin, nous tenterons d’établir le lien entre la turbulence, la contrainte de cisaillement et l’érosion des berges.
Méthodologie
Site d’étude
Le site d’étude est une section de 70 m de long sur la rivière Petite Barbue, à environ 60 km à l’est de Montréal (Québec). Il s’agit d’une boucle de méandre de près de 180°, avec, au niveau plein bord (débit d’environ 10 m3/s), une profondeur maximale de 3,2 m, une largeur de 11,5 m et un rayon de courbure de 18,5 m. Le lit est composé de sables ayant un D50 de 0,38 mm et un D84 de 0,92 mm. Quelques rides étaient présentes sur le lit lors des périodes d’échantillonnage, principalement à l’entrée du méandre, avec une hauteur d’environ 10 mm et une longueur d’onde de près de 35 mm. Les berges sont composées d’un mélange d’argile et de limon, et la berge externe est presque verticale. Plusieurs exemples de décrochement des berges sont évidents sur ce site, tels qu’illustrés à la figure 1A. Contrairement à ce qui est souvent prédit (Whiting et Dietrich, 1993), l’érosion semble plus active à l’entrée et à la sortie du méandre, plutôt qu’à son apex (fig. 1A).
Figure 1
A)
B)
(A) Vue vers l’aval de la portion amont et aval du méandre montrant des signes d’érosion. (B) Emplacement des deux profils verticaux utilisés pour la comparaison des vitesses moyennes, turbulentes et de contraintes de cisaillement entre l’ADV et le PC-ADP.
(A) Downstream view showing the upstream and downstream part of of the meander loop where bank erosion is active. (B) Position of the two vertical profiles for the comparison of mean and turbulent velocities, and bed shear stress between the ADV and PC-ADP.
Les données de topographie du lit et des berges, ainsi que celles de vitesses ont été recueillies en 2002 et en 2003. La topographie a été mesurée avec une station totale Leica TC805L. Des repères permanents ont été utilisés afin de permettre la comparaison d’un relevé à l’autre. Une sonde à pression fournissait aussi des données de niveau d’eau en continu pendant ces deux années.
Appareils de mesure de vitesse
Les données de vitesse 3D ont été prises à l’aide de deux appareils de mesure : un ADV et un PC-ADP (Pulse-Coherent Acoustic Doppler Profiler). Les deux appareils sont basés sur le principe du décalage Doppler. Toutefois, l’ADV ne mesure qu’un point à la fois, dans un petit volume de mesure (environ 1 cm3) situé 5 cm sous les émetteurs (fig. 2A), à une fréquence d’échantillonnage de 25 Hz. Le PC-ADP est semblable à l’ADCP, fréquemment utilisé sur des grandes rivières où les mesures sont prises à partir d’un bateau, car il mesure simultanément les vitesses le long d’un profil vertical, à une fréquence de 2 Hz (fig. 2B). La taille minimum des cellules de mesure de l’ADCP ne procure toutefois pas une résolution acceptable dans la zone proximale du lit (Lacy et Sherwood, 2004) et il est en général impossible de prendre des mesures à moins de 1 à 1,5 m du lit (Dinehart et Burau, 2005 ; Shields et Rigby, 2005). Le PC-ADP résout en partie ces problèmes. Son utilisation est limitée à des cours d’eau de profondeurs de 1 à 2 m, et la taille minimum des cellules est un ordre de grandeur inférieure à celle de l’ADCP (Lacy et Sherwood, 2004). La largeur du signal acoustique émis par le PC-ADP du centre du faisceau jusqu’à sa bordure est de 15° (au lieu de 20 à 30° pour l’ADCP). L’extension latérale du volume de mesure augmente donc au fur et à mesure que l’on s’éloigne de l’appareil (fig. 2B). Par contre, la dimension verticale du volume de mesure est déterminée par l’usager (fixée ici à 45 mm). Le PC-ADP ne peut pas mesurer l’écoulement dans la portion la plus haute de la tranche d’eau ; une valeur de 10 cm a été utilisée comme distance de suppression (blanking distance) dans cette étude.
Figure 2
A)
B)
Les différences entre les volumes de mesure des deux appareils : (A) ADV et (B) PC-ADP.
Differences in sampling volumes between the two measuring devices : (A) ADV and (B) PC-ADP.
Les deux appareils de mesure étaient montés sur une perche de métal, semblable à celle décrite dans Lane et al. (1998), conçue avec un bras en U pour permettre de coulisser les vélocimètres aisément sur la verticale tout en s’assurant d’être à une distance suffisamment grande en amont de la perche pour que celle-ci n’affecte pas l’écoulement. Deux prismes étaient installés sur le haut de la perche afin de permettre de positionner les mesures de vitesse dans le même système de coordonnées que celui de la topographie du lit. Ce système à deux prismes a été développé par Lane et al. (1998) afin d’effectuer une rotation des données pour s’assurer que les composantes longitudinale (Vx) et latérale (Vy) des mesures d’ADV étaient toujours alignées selon une même direction en X et en Y pour l’ensemble de la section d’étude. Cette approche est valable pour une rivière rectiligne, mais nous avons dû la modifier pour une section courbe.
Plusieurs méthodes existent pour effectuer une rotation des coordonnées dans des chenaux courbes. Par exemple, les composantes longitudinale et latérale peuvent être pivotées afin d’être parallèles et perpendiculaires à la direction moyenne de l’écoulement à une coupe transversale, en utilisant l’approche de Rozovskii pour définir cette direction (Rhoads et Kenworthy, 1998). Cette méthode, bien que critiquée par certains (Lane et al., 1999), permet de bien cerner les cellules d’écoulement secondaire (Rhoads et Kenworthy, 1999) et a été utilisée pour les données du PC-ADP. Pour l’ADV, la rotation s’est effectuée en fonction de l’orientation des berges, c’est-à-dire les composantes longitudinale et latérale étaient parallèles et perpendiculaires, respectivement, aux berges de chaque coupe transversale. Ceci avait pour but de favoriser l’étude des structures turbulentes, où le système de référence doit être cohérent d’un point de mesure à l’autre (Roy et al., 1996). Les deux méthodes sont décrites en détail dans Tilston (2006).
Une comparaison détaillée de la performance de chaque appareil pour l’analyse des signaux de vitesse moyenne et turbulente a été effectuée pour un débit équivalent à 40 % du niveau plein bord (tabl. I) à deux profils verticaux situés dans des zones d’écoulement distinctes à l’entrée du méandre (fig. 1B) : (1) une position centrale d’une profondeur de 0,86 m et (2) une position dans le plan de mélange engendré par les anfractuosités de la berge d’une profondeur de 0,66 m. Les profils du PC-ADP contiennent 16 et 12 points, respectivement, à chaque position, d’une durée de 905,5 s à une fréquence de 2 Hz, tandis que les profils d’ADV contiennent 12 et 11 points, respectivement, d’une durée de 140 s à 25 Hz. Pour cette comparaison, les deux appareils étaient positionnés le plus exactement possible au même endroit. Un profil avec le PC-ADP était mesuré, suivi d’un profil avec l’ADV, avant de déplacer les deux appareils à l’autre emplacement. Le délai maximum entre les mesures était donc très court (environ 30 min), pendant lequel le niveau d’eau est demeuré constant.
Tableau I
Dates des campagnes d’échantillonnage et types de mesure dans chaque cas
Structure de l’écoulement dans un méandre
Afin d’examiner la structure turbulente de l’écoulement au sein du site d’étude, des mesures d’ADV ont été prises à quatre positions latérales le long de sept coupes transversales réparties régulièrement entre l’entrée et la sortie du méandre. Dépendant de la profondeur, deux à trois positions verticales étaient échantillonnées pour une durée de deux minutes à une fréquence de 25 Hz pour obtenir une bonne caractérisation de la turbulence de l’écoulement. Ces données ont été traitées afin d’éliminer les mesures dont la corrélation était inférieure à 70 % (Lane et al., 1998). Les données extrêmes (spikes) ont été éliminées à l’aide de la méthode de seuil espace-phase (phase-space threshold) de Goring et Nikora (2002). Enfin, la contamination par le bruit Doppler dans les hautes fréquences (McLelland et Nicholas, 2000) a été corrigée en utilisant un filtre passe-bas Chebyshev (type I) (Nicholas, 2001). Deux séries de mesure (15 et 27 mai 2003), correspondant à des débits de 33 et 28 % du niveau plein bord, seront examinées ici.
La structure moyenne de l’écoulement a aussi été examinée à l’aide de deux séries de mesure de PC-ADP à des coupes transversales situées à l’entrée et à l’apex (28 août 2003, 21 % du niveau plein bord), ainsi qu’à la sortie (13 octobre 2003, 29 % du niveau plein bord) du méandre. À chaque coupe, six à neuf positions latérales ont été échantillonnées pour une période de 15 min à une fréquence de 2 Hz. Le nombre total de mesures était fonction de la profondeur de l’écoulement à chaque emplacement. Le tableau I résume l’information concernant les dates des campagnes de terrain ainsi que les actions conduites dans chaque cas.
Il est à noter que des travaux de stabilisation des berges ont été effectués au site d’étude en juin 2003 (fig. 3). La pente de la berge externe a été réduite à 30°, et de la végétation arbustive résistante à l’eau a été plantée entre le haut de la berge et le niveau d’eau considéré moyen. Les données d’ADV ont été recueillies avant que ces modifications ne soient apportées, tandis que celles du PC-ADP ont été prises deux et quatre mois plus tard. Toutefois, l’impact de la stabilisation sur les données hydrauliques prises avec le PC-ADP est minime puisque le niveau d’eau était inférieur à la limite des changements apportés à la berge.
Figure 3
Travaux de stabilisation des berges, à l’aide d’un adoucissement de la pente de la berge externe (30°) et de l’ajout de végétation, effectués en juin 2003 au site d’étude (vue vers l’aval).
Bank stabilization work, consisting in a decreased external bank slope (30°) and added vegetation, implemented in June 2003 at the field site (downstream view).
Contrainte de cisaillement
En plus des vitesses moyennes et des écarts-types, différents estimés de contrainte de cisaillement (T0) ont été analysés à l’aide de l’ADV et du PC-ADP pour les deux profils verticaux décrits précédemment, aux positions indiquées à la figure 1B. Six méthodes sont comparées, trois d’entre elles utilisant la vitesse moyenne, et les trois autres les fluctuations turbulentes. Ces méthodes possèdent chacune des avantages et des inconvénients qui sont décrits en détail dans Dietrich et Whiting (1989) et Biron et al. (2004).
Parmi les approches utilisant la vitesse moyenne, la plus populaire est sans doute la méthode du profil logarithmique :
où T0 est la contrainte de cisaillement, u est la vitesse à une hauteur donnée au-dessus du lit, к est la constante de Von Karman (~0,4), z est la hauteur au-dessus du lit et z0 le paramètre de rugosité. La contrainte de cisaillement peut aussi être calculée par la méthode de traînée (drag) :
où U est la vitesse moyenne, ρ est la densité du fluide et CD est le coefficient de traînée (drag coefficient). Enfin, il est possible de modifier l’équation 1 de sorte qu’une seule mesure de vitesse soit requise à 20 mm au-dessus du lit. Ici, z0 peut être estimé par :
où A est une constante empirique, D est une échelle de longueur des particules contrôlant la résistance où x représente le pourcentage plus fin que cette taille de particule, et R* est le nombre de Reynolds de rugosité (Dietrich et Whiting, 1989). Cette équation peut se simplifier à :
où 84 % des sédiments sont plus fins que la taille représentée par D84.
Parmi les méthodes utilisant les fluctuations turbulentes, la contrainte de cisaillement de Reynolds est la plus populaire :
où ![]() est la moyenne des fluctuations instantanées de vitesse dans le plan horizontal (u′) et vertical (w′) (Clifford et French, 1993). Cette méthode possède toutefois l’inconvénient d’être difficile à appliquer lorsque les senseurs de vitesse ne sont pas parfaitement orientés par rapport à la direction du courant (Stapleton et Huntley, 1995 ; Wolf, 1999 ; Kim et al., 2000), ce qui est souvent le cas dans un méandre. De plus, dans les problèmes d’érosion de berge, il n’est pas évident que le plan horizontal et vertical soit le plus approprié — on pourrait penser que le plan horizontal et latéral serait à même de mieux cerner les forces appliquées sur la berge. Le problème de l’orientation des senseurs peut être surmonté si l’on utilise les trois composantes de l’écoulement dans la méthode de l’énergie turbulente cinétique (TKE) :
est la moyenne des fluctuations instantanées de vitesse dans le plan horizontal (u′) et vertical (w′) (Clifford et French, 1993). Cette méthode possède toutefois l’inconvénient d’être difficile à appliquer lorsque les senseurs de vitesse ne sont pas parfaitement orientés par rapport à la direction du courant (Stapleton et Huntley, 1995 ; Wolf, 1999 ; Kim et al., 2000), ce qui est souvent le cas dans un méandre. De plus, dans les problèmes d’érosion de berge, il n’est pas évident que le plan horizontal et vertical soit le plus approprié — on pourrait penser que le plan horizontal et latéral serait à même de mieux cerner les forces appliquées sur la berge. Le problème de l’orientation des senseurs peut être surmonté si l’on utilise les trois composantes de l’écoulement dans la méthode de l’énergie turbulente cinétique (TKE) :
où v’ représente les fluctuations de la composante latérale de vitesse et C1 est une constante de proportionnalité (~0,19) (Soulsby, 1983 ; Kim et al., 2000 ; Biron et al., 2004). Une variante de cette méthode a été proposée par Kim et al. (2000) qui soulèvent le problème du bruit Doppler plus marqué dans les composantes horizontales (u et v) que verticale de l’ADV, et qui n’utilisent donc que la composante verticale :
où c2 est un coefficient égal à 0,9 (Kim et al., 2000).
Résultats
Comparaison ADV et PC-ADP
Vitesses moyennes
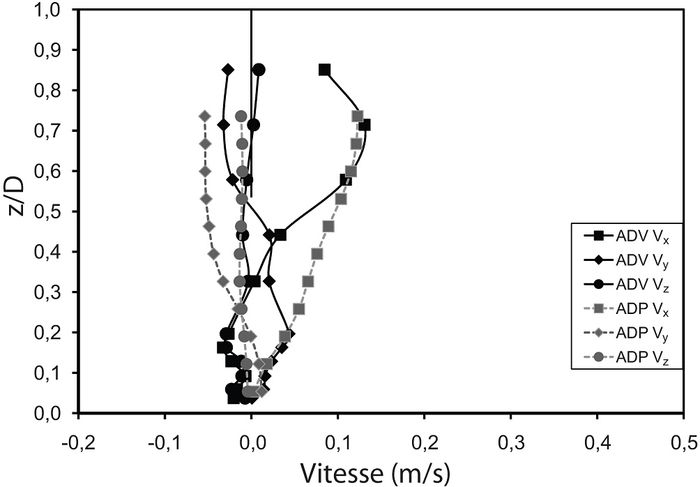
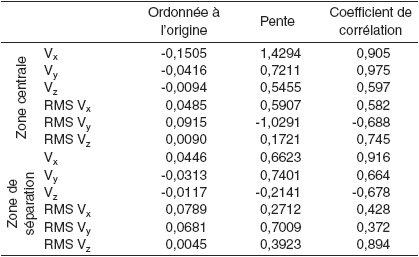
La figure 4 présente une comparaison des mesures obtenues avec l’ADV et le PC-ADP pour les deux profils (fig. 1B) recueillis dans des zones que l’on nommera « centrale » (fig. 4A) et « de séparation » (fig. 4B). Dans la zone centrale, la composante longitudinale (Vx) pour les deux appareils révèle clairement un profil logarithmique. De plus, les courants secondaires sont systématiquement dirigés vers la berge externe près de la surface de l’eau (vitesses latérales (Vy) négatives), avec du downwelling près de la berge (vitesses verticales (Vz) négatives), et sont dirigés vers la berge interne (Vy positif) près du lit. Dans l’ensemble, les deux appareils procurent des résultats assez conformes dans la portion la plus élevée de la tranche d’eau. Il semble toutefois que le PC-ADP surestime les vitesses longitudinales, avec une pente de 1,43 et une ordonnée à l’origine négative (‑0,15) (tabl. II). La composante latérale est par contre systématiquement plus faible pour le PC-ADP que pour l’ADV (pente de 0,72), et cette différence s’accroît vers le lit (fig. 4A). Les coefficients de corrélation sont toutefois élevés pour les deux composantes horizontales (0,91 et 0,98 pour Vx et Vy, respectivement) (tabl. II). Un problème d’alignement des senseurs pourrait expliquer une différence constante entre les valeurs telle qu’observée pour Vy, mais pas la variation de la surface vers le lit.
Figure 4
A)
B)
Comparaison des valeurs de vitesse moyenne pour les trois composantes de l’écoulement entre l’ADV et le PC-ADP dans (A) la zone centrale (position 1, fig. 1B) et (B) la zone de séparation (position 2, fig. 1B).
Comparison of mean velocity values for the three velocity components between the ADV and PC-ADP in (A) the central zone (position 1, Fig. 1B) and (B) the separation zone (position 2, Fig. 1B).
Tableau II
Comparaison entre les pentes, les ordonnées à l’origine (régression des moindres carrés du PC-ADP en fonction de l’ADV) et les coefficients de corrélation entre l’ADV et du PC-ADP pour les moyennes et les écarts-types (RMS) dans les deux zones (centrale et de séparation)
La situation est très différente dans la zone de séparation (fig. 4B). Bien que le coefficient de corrélation demeure élevé entre les deux appareils pour Vx (0,92) (tabl. II), il est fortement réduit pour la composante latérale (0,66) et il est même négatif pour la composante verticale (‑0,68). De plus, les pentes sont nettement inférieures à l’unité pour toutes les composantes de vitesse. Les deux appareils procurent des données relativement conformes seulement dans la portion plus élevée de la colonne d’eau (25 % du haut). Dans le bas du profil, l’ADV indique que l’écoulement est orienté vers l’amont (Vx négatifs), tandis que le PC-ADP montre une décroissance linéaire de la vitesse vers le lit, mais avec une orientation toujours vers l’aval (fig. 4B). Les problèmes d’alignement pourraient expliquer en partie ces différences, mais il est aussi fort probable que le moyennage spatial joue un rôle important. En effet, étant donné que le volume de mesure du PC-ADP augmente vers le lit, les mesures peuvent être contaminées soit par la berge, du côté droit, soit parce que la moyenne des vitesses inclut des valeurs de l’autre côté du plan de mélange du côté gauche. L’écoulement secondaire présente par contre certaines caractéristiques semblables entre les deux appareils, soit une orientation vers la berge externe près de la surface de l’eau, et un courant dirigé vers la berge interne près du lit (fig. 4B). La différence entre les vitesses latérales observée dans la zone centrale est aussi présente.
Turbulence
La figure 5 illustre les profils de turbulence (écart-type) entre les deux appareils. Dans la zone centrale (fig. 5A), les valeurs d’écart-type de Vx sont à leur maximum approximativement à 20 % de la profondeur d’eau, et diminuent ensuite vers la surface de l’eau pour les deux appareils. Ceci correspond bien à ce qui est anticipé à l’entrée d’une mouille (Song et Chiew, 2001). De même que pour la vitesse moyenne, les différences entre les appareils augmentent en s’approchant du lit, mais la comparaison des données turbulentes est en général nettement moins bonne tout au long du profil, avec des coefficients de corrélation plus faibles (négatifs pour Vy) et des pentes assez proches de 0 (tabl. II). Les problèmes d’alignement ne peuvent qu’en partie expliquer ces différences, qui reflètent sans doute la plus grande sensibilité des statistiques turbulentes aux différences de taille de volume de mesure et de fréquence d’échantillonnage.
Figure 5
A)
B)
Comparaison des valeurs d’écart-type pour les trois composantes de l’écoulement entre l’ADV et le PC-ADP dans (A) la zone centrale (position 1, fig. 1B) et (B) la zone de séparation (position 2, fig. 1B).
Comparison of RMS values for the three velocity components between the ADV and PC-ADP in (A) the central zone (position 1, Fig. 1B) and (B) the separation zone (position 2, Fig. 1B).
Dans la zone de séparation, les données sont très différentes pour les trois composantes de vitesse (fig. 5B). Ceci n’est pas vraiment étonnant compte tenu que le patron des vitesses moyennes montrait déjà des variations importantes. Encore ici, le volume de mesure nettement plus grand du PC-ADP fait en sorte que les valeurs d’écart-type représentent une portion des fluctuations de vitesse engendrées par le plan vertical de mélange, qui peuvent être substantielles (De Serres et al., 1999).
Contrainte de cisaillement
L’estimé de la contrainte de cisaillement dans les méandres est notoirement complexe en raison des changements rapides d’orientation de l’écoulement et du rôle joué par le gradient de pression et la topographie variable du lit (Whiting et Dietrich, 1991). Durant la prise de mesure, de petites rides étaient présentes et des mouvements sporadiques de particules au lit ont été observés dans la zone centrale. Les données recueillies sur ce profil sont utilisées pour analyser les différentes méthodes d’estimés de la contrainte de cisaillement, en les comparant à la contrainte critique de Shields (Knighton, 1998). La supposition est qu’une valeur appropriée de contrainte de cisaillement devrait être légèrement supérieure à la contrainte critique, ce qui expliquerait les observations qualitatives de transport sporadique en charge de fond.
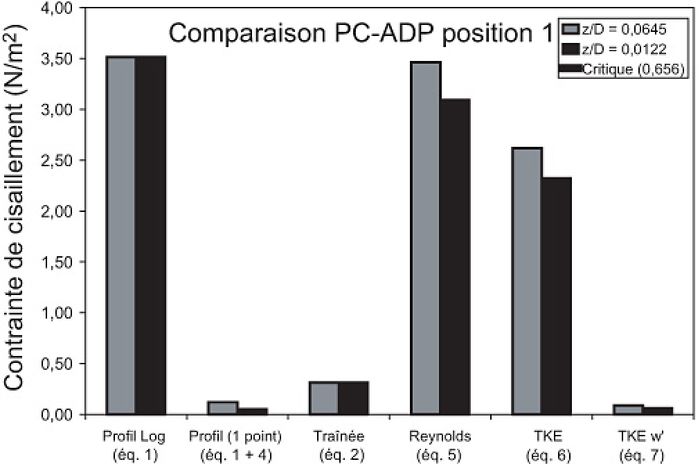
La figure 6 présente les résultats pour les deux appareils à deux hauteurs au-dessus du lit pour les équations 1 à 6. Pour l’ADV (fig. 6A), deux des trois méthodes basées sur la turbulence (Reynolds et TKE) produisent systématiquement des valeurs de contrainte de cisaillement supérieures à celles obtenues par les vitesses moyennes. Ces dernières sont nettement en dessous de la contrainte critique de Shields (0,66 N/m2) requise pour initier le transport des particules, ce qui contredit les observations de terrain de transport sporadique. Des différences comparables entre les méthodes moyennes et turbulentes avaient été notées par Drake et al. (1988) en présence de transport sous forme de poches discrètes dans le temps et dans l’espace. Ceci suggère que les méthodes de contrainte de Reynolds et de TKE sont plus appropriées dans les études de transport de sédiments.
Figure 6
A)
B)
Comparaison de différents estimés de contrainte de cisaillement dans la zone centrale (position 1, fig. 1B) pour (A) l’ADV et (B) le PC-ADP.
Comparison of bed shear stress values in the central zone (position 1, Fig. 1B) for (A) the ADV and (B) the PC-ADP.
Par contraste, les résultats obtenus avec le PC-ADP montrent que les contraintes de cisaillement diffèrent de quelques ordres de grandeur entre les méthodes moyennes et turbulentes (fig. 6B). Les estimés par la méthode de traînée (éq. 2) et la méthode de profil logarithmique en un point (éq. 3) sont nettement sous le seuil critique requis pour initier un mouvement de particules. Par contre, les méthodes de profil logarithmique traditionnel, de contrainte de Reynolds et de TKE produisent des valeurs de près de 3,2 N/m2, ce qui permettrait en théorie de déplacer des particules jusqu’à 4,5 mm. Les observations de terrain montrent que le taux de transport était nettement inférieur à ce que ces estimés indiquent. En ce qui a trait à la méthode turbulente par la vitesse verticale (éq. 7), les estimés sont trop faibles.
Ces résultats confirment les conclusions tirées des données en laboratoire de Biron et al. (2004) selon lesquelles les méthodes de turbulence de Reynolds et TKE fournissent des estimés de contrainte de cisaillement plus appropriés dans un écoulement complexe. Toutefois, en raison du problème d’alignement des senseurs dans les estimés de contrainte de Reynolds — problème accentué dans le cas d’un méandre —, nous avons opté pour la méthode TKE, conformément aux recommandations de Biron et al. (2004).
Le moyennage spatial du PC-ADP étant un problème pour l’analyse des signaux turbulents près du lit (fig. 4B et 5B), cet appareil ne sera pas utilisé pour examiner les patrons de contrainte de cisaillement. Par contre, le PC-ADP procure une densité de mesures nettement supérieure à celle obtenue par l’ADV, et est donc mieux adapté pour décrire la structure moyenne de l’écoulement.
Structure de l’écoulement moyen et turbulence
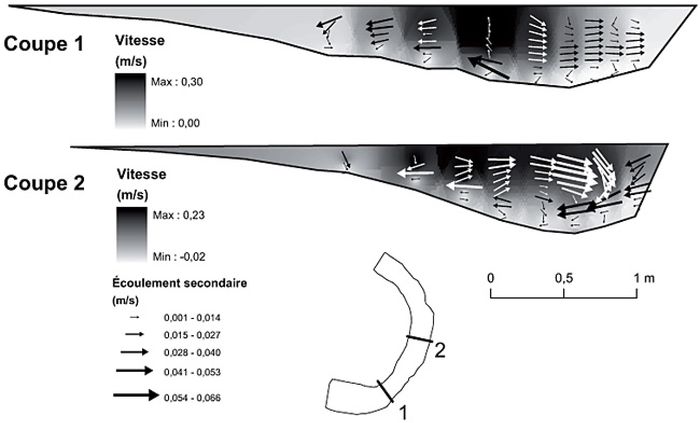
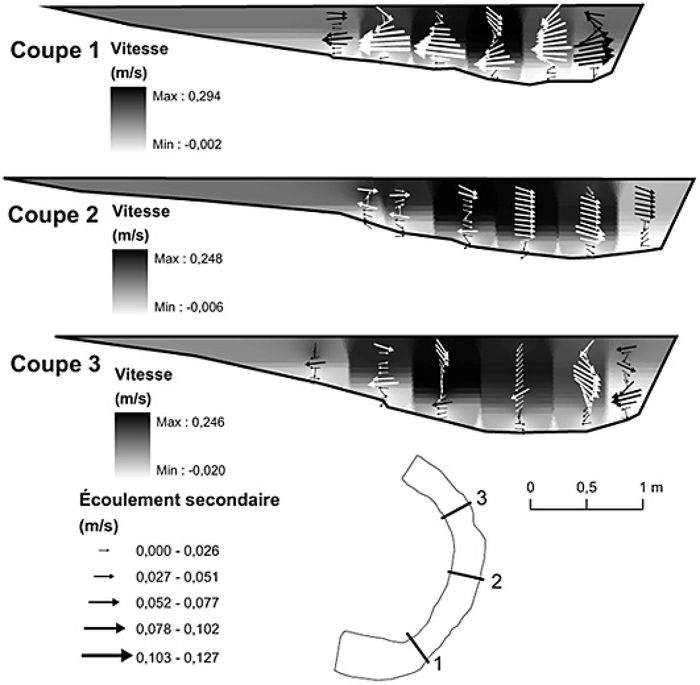
Les vitesses moyennes et l’écoulement secondaire sont présentés à la figure 7. Pour les deux périodes de mesure, la vitesse maximale diminue de l’entrée vers l’apex et la sortie (0,30 m/s à l’entrée et 0,23 m/s à l’apex pour le 28 août ; 0,29 m/s à l’entrée et 0,25 m/s à l’apex pour le 13 octobre). Le 28 août, une cellule d’écoulement secondaire est nettement présente à l’apex (fig. 7A), avec une petite cellule de plus faible intensité près de la berge. Le 13 octobre, deux cellules d’écoulement secondaire peuvent être distinguées, particulièrement à l’entrée (coupe 1), avec la cellule principale occupant une grande portion de la zone centrale du chenal, et une plus petite cellule de sens contraire près de la berge (fig. 7B). Cette dernière ne semble toutefois pas persister vers l’aval où le patron d’écoulement secondaire est complexe. Il est possible que cette moins grande cohérence soit liée à un nombre plus restreint de mesures, avec 6 profils plutôt que 9 le 13 octobre.
Figure 7
A)
B)
Vitesse moyenne et vecteurs d’écoulement secondaire superposés, mesurés avec le PC-ADP. (A) 28 août 2003 (21 % niveau plein bord) et (B) 13 octobre 2003 (29 % niveau plein bord). Deux couleurs de vecteurs sont utilisées afin de bien les distinguer de l’arrière-plan.
colors are used for velocity vectors to distinguish them from the background color.
Mean velocity and superimposed secondary current vectors, measured with the PC-ADP. (A) August 28, 2003 (21% of bankfull discharge) and (B) October 13, 2003 (29% of bankfull discharge). Two
La figure 8 montre les intensités turbulentes des composantes longitudinale, latérale et verticale pour les deux conditions d’écoulement, et ce, près du lit et près de la surface de l’eau. Au niveau d’eau plus bas (fig. 8I), les valeurs d’intensité turbulente (calculées en pourcentage de l’écart-type à chaque emplacement divisé par la vitesse moyenne à l’entrée du méandre) sont en général plus élevées pour la composante longitudinale que pour les deux autres composantes, et près du lit que plus haut dans la tranche d’eau. Les distributions spatiales indiquent que les zones d’intensité turbulente plus élevées, pour l’ensemble des données, se trouvent près de la berge externe à l’entrée et à la sortie du méandre. Lorsque le débit est plus élevé (fig. 8II), la zone de turbulence accrue à l’entrée tend à s’amenuiser alors qu’elle est plus marquée à la sortie pour les trois composantes de l’écoulement aux deux hauteurs de mesure.
Figure 8
I
II
Intensité turbulente près de la surface pour la composante longitudinale (A), latérale (B) et verticale (C), et près du lit pour la composante longitudinale (D), latérale (E) et verticale (F) le 27 mai 2003 (I) (niveau d’eau plus bas) et le 15 mai 2003 (II) (niveau plus élevé).
Turbulence intensity near the surface for the longitudinal (A), lateral (B) and vertical (C) components, and near the bed for the longitudinal (D), lateral (E) and vertical (F) components on May 27, 2003 (I) (lower flow stage), and May 15, 2003 (II) (higher flow stage).
Ces patrons d’intensité turbulente se répercutent nécessairement sur les mesures de contrainte de cisaillement puisque la méthode TKE utilise les fluctuations de vitesse des trois composantes de l’écoulement. La figure 9 présente la topographie du lit, les vecteurs de vitesse près du lit et à la surface ainsi que la contrainte de cisaillement TKE pour les deux mêmes conditions d’écoulement qu’à la figure 8. Au niveau plus bas, le méandre est caractérisé par des zones de surcreusement multiples, plutôt que par une large mouille (fig. 9IA). La présence d’une cellule d’écoulement secondaire révélée par les données de PC-ADP est ici aussi visible par les différences d’orientation entre les vecteurs près de la surface et près du lit (fig. 9IB). Les plus fortes contraintes de cisaillement se retrouvent près de l’entrée du méandre (fig. 9IC). Au niveau d’eau plus élevé, les profondeurs sont plus homogènes et moins de poches de surcreusement sont visibles, donnant lieu à une mouille persistant de la zone un peu en amont de l’apex jusqu’à la sortie du méandre (fig. 9IIA). La présence d’une cellule d’écoulement secondaire importante est encore évidente (fig. 9IIB). Par contre, la distribution spatiale de la contrainte de cisaillement diffère de celle de plus faible débit. Les valeurs les plus fortes se trouvent vers la sortie du méandre plutôt qu’à son entrée (fig. 9IIC).
Figure 9
I
II
(A) Topographie du lit, (B) vecteurs d’écoulement moyen près du lit (flèches noires) et près de la surface (flèches grises) et (C) contrainte de cisaillement (méthode TKE) avec les contours d’élévation pour le 27 mai 2003 (I) (niveau d’eau plus bas) et le 15 mai 2003 (II) (niveau plus élevé).
(A) Bed topography, (B) mean flow vectors near the bed (black arrows) and near the water surface (grey arrows), and (C) bed shear stress (TKE method) with contour of bed topography for May 27, 2003 (I) (lower flow stage), and May 15, 2003 (II) (higher flow stage).
Discussion
PC-ADP versus ADV
La compréhension de la dynamique de l’écoulement dans un environnement complexe comme une boucle de méandre requiert une grande densité de mesures de vitesse 3D, idéalement simultanées. Ceci est relativement aisé en laboratoire, par exemple avec des profileurs Doppler miniatures (Blanckaert et Graf, 2001) ou par des mesures de vitesse par imagerie de particules (PIV). Les mesures de terrain sont toujours plus complexes à recueillir, mais les progrès technologiques récents augmentent grandement notre capacité de quantifier adéquatement la dynamique de l’écoulement dans les rivières. La plus récente innovation dans la mesure simultanée de profils de vitesse dans des rivières peu profondes est le PC-ADP. Cette étude, tout comme celle de Dinehart et Burau (2005) qui utilisaient un ADCP dans une rivière plus profonde, montre que les écoulements secondaires caractéristiques des méandres sont très bien dépeints par les profils simultanés de vitesse 3D. Ceci constitue une nette amélioration sur les mesures ponctuelles de la vitesse 3D obtenues avec un ADV (Frothingham et Rhoads, 2003 ; Daniel et Rhoads, 2004 ; Rodriguez et al. 2004), qui elles-mêmes constituaient un grand progrès par rapport aux données en deux dimensions mesurées à l’aide de courantomètres électromagnétiques ou à hélice (vitesses longitudinales et latérales) qui ont longtemps été utilisées sur ces sites (Dietrich et Smith, 1983).
Cette nouvelle technologie doit par contre être bien testée avant de conclure qu’elle est supérieure ou comparable aux technologies existantes. Une comparaison détaillée entre un PC-ADP et un ADV a été réalisée récemment par Lacy et Sherwood (2004) dans un environnement littoral. Cette étude confirme nos observations en ce qui concerne la vitesse moyenne dans un environnement « relativement » simple, soit le centre du chenal d’une boucle de méandre, et un écoulement dominé par les vagues dans le cas de Lacy et Sherwood (2004). Ces derniers ont toutefois noté que l’erreur due à l’ambiguïté devait être corrigée pour des vitesses plus élevées (>0,50 m/s). Bien que qualitativement, les profils de vitesse obtenus à l’aide de l’ADV et du PC-ADP soient semblables à la position 1 (fig. 4A), des divergences assez importantes surviennent près du lit dans notre étude, ce qui n’était pas le cas dans celle de Lacy et Sherwood (2004). Ceci s’explique d’une part par le moyennage spatial qui augmente près du lit, et d’autre part par la présence d’un plan de cisaillement lié à l’irrégularité de la berge. En effet, une partie du volume de mesure près du lit dans la zone centrale du chenal inclut la zone de séparation de vitesse plus faible, tandis que le haut du profil de mesure du PC-ADP est entièrement dans la zone centrale. Ceci pourrait expliquer l’ordonnée à l’origine négative (‑0,15 m/s) et la pente supérieure à 1 (1,43) dans l’analyse de régression du PC-ADP en fonction de l’ADV (tabl. II). La concordance entre le PC-ADP et l’ADV est en général nettement moins bonne dans la zone de séparation, où le problème de moyennage spatial se fait sentir sur presque toute la profondeur du profil en raison du gradient latéral élevé des vitesses (fig. 4B).
Les données turbulentes révèlent par contre des différences plus importantes entre le PC-ADP et l’ADV. Ceci n’est pas étonnant puisque la variabilité spatiale des propriétés turbulentes dans un écoulement complexe comme une boucle de méandre est plus grande que celle des propriétés moyennes (Blanckaert et Graf, 2001). De plus, la différence de fréquence d’échantillonnage entre les deux appareils (2 Hz et 25 Hz pour le PC-ADP et l’ADV, respectivement) entre en jeu. La perte de variance due à une fréquence d’échantillonnage trop faible peut être considérable dans des chenaux de la taille de la rivière Petite Barbue où les structures turbulentes sont de petites tailles (Soulsby, 1980 ; Roy et al., 1997). Lorsque l’on utilise un filtre passe-bas (moyenne mobile) afin de décimer le signal d’ADV à une fréquence de 2 Hz pour calculer les écarts-types des vitesses recueillies avec l’ADV, les valeurs dans la zone centrale diminuent en moyenne de 15, 20 et 30 % pour les composantes de vitesse longitudinale, latérale et verticale, respectivement. Les plus importantes pertes surviennent dans la composante verticale, car elle est caractérisée par des fluctuations de plus hautes fréquences que la composante longitudinale (Heathershaw, 1979 ; Roy et al., 1997). La perte de variations turbulentes dans les hautes fréquences avec le PC-ADP, combinée au problème de moyennage spatial, implique qu’il ne s’agit vraisemblablement pas d’un instrument approprié pour des études de structures cohérentes de petite taille (par exemple les cycles d’éjection et d’incursion).
Peu d’études ont mesuré la distribution spatiale de la contrainte de cisaillement au lit dans des boucles de méandre en milieu naturel. À notre connaissance, cette étude est la première à utiliser une méthode basée sur les fluctuations turbulentes dans une section curviligne afin de quantifier cette variable. La comparaison des différents estimés de contrainte corrobore les résultats obtenus par Biron et al. (2004) autour de déflecteurs de courant qui montrent que les méthodes de calcul de la contrainte de cisaillement basées sur les fluctuations turbulentes de vitesse (Reynolds et TKE) sont plus appropriées dans un écoulement complexe. Il n’est alors pas étonnant que cette étude conclue que l’ADV procure des estimés de contrainte au lit nettement plus adéquat que le PC-ADP, puisque ce dernier souffre de lacunes importantes en ce qui a trait à la mesure de la turbulence.
Par contre, les nombreuses mesures simultanées de vitesse du PC-ADP permettent d’investiguer les structures cohérentes à grande échelle, comme celles décrites par Buffin-Bélanger et al. (2000) dans les rivières à lit graveleux, dont la durée est suffisamment longue (ou la vitesse assez faible) pour permettre de recueillir un nombre suffisant de profils simultanés. Une telle analyse a été effectuée dans le cadre de cette étude (données non présentées ici). Le moyennage temporel du PC-ADP s’est alors avéré un avantage, car il élimine le bruit des hautes fréquences et permet de distinguer aisément le passage de structures à grande échelle rapides et lentes dans le méandre dans les plans horizontal, vertical et latéral (Tilston, 2006). En cela, le PC-ADP procure un net avantage par rapport à l’ACDP dont la fréquence d’échantillonnage est semblable (1 Hz), mais qui ne peut résoudre les variations à petites échelles spatiales (Shields et Rigby, 2005).
Structure de l’écoulement moyen et turbulence
Le patron de cellules hélicoïdales obtenu à l’aide du PC-ADP (fig. 7) est conforme à ce qui est anticipé dans une boucle de méandre, soit une cellule principale circulant dans le sens des aiguilles d’une montre (en regardant vers l’aval), et une plus petite cellule de direction opposée (Rhoads et Welford, 1991 ; Whiting et Dietrich, 1991 ; Knighton, 1998). Ce patron ne ressort toutefois pas aussi bien que celui obtenu à l’aide d’un ADCP par Dinehart et Burau (2005) sur la rivière Sacramento (largeur de près de 150 m) en raison de la plus petite taille du cours d’eau et de l’impact relativement plus grand des effets de berge (et notamment du plan de cisaillement). Par contre, si l’on postule que des mesures détaillées de vitesse sont requises près des berges afin de déterminer plus précisément le lien entre l’hydraulique et l’érosion des berges dans les méandres, le PC-ADP souffre alors du problème de moyennage spatial qui contamine le signal de vitesse puisque le cône de mesure inclut une portion grandissante de la berge au fur et à mesure que l’on se rapproche du lit.
Les trois composantes de l’écoulement suivent une distribution spatiale d’intensité turbulente semblable au lit et à la surface, avec des valeurs allant en décroissant de la composante longitudinale, à latérale et enfin verticale, conformément à ce qui est attendu (Blanckaert and Graf, 2001 ; Song and Chiew, 2001). La position des maxima d’intensité turbulente est toutefois fonction des conditions d’écoulement. Au niveau plus bas, les intensités turbulentes sont à leur maximum près de l’entrée du méandre, tandis que ceci se produit plus près de la sortie du méandre lorsque le niveau augmente (fig. 8). Le même patron est observé pour les contraintes de cisaillement par la méthode TKE (fig. 9), ce qui n’est pas surprenant compte tenu du lien étroit entre ces deux variables. Cette transition corrobore les observations de Chang (2002), comme quoi la zone d’érosion maximum dans les boucles de méandre se déplace vers la sortie de la boucle lorsque le débit augmente.
Des mesures de topographie du lit et des berges prises au printemps 2004, soit une année après les travaux de stabilisation de berge, montrent que les zones d’érosion des berges nouvellement modifiées se situent là où les contraintes de cisaillement étaient les plus élevées, soit à l’entrée (niveau d’eau plus bas) et à la sortie (niveau d’eau plus élevé) du méandre (fig. 10). Il est encore trop tôt pour conclure sur l’efficacité de ces mesures de stabilisation de berge, mais les évidences de décrochement si tôt après les travaux indiquent peut-être que les zones de fortes contraintes de cisaillement à l’entrée et à la sortie du méandre devraient bénéficier d’une protection supplémentaire dans les aménagements futurs.
Figure 10
Zones d’érosion et de dépôt de sédiments observées un an après les travaux de stabilisation de berge.
Erosion and deposition zones observed one year after the bank stabilization work.
Conclusion
Cette recherche a montré que la présence de deux cellules d’écoulement secondaire dans un méandre naturel est très bien quantifiée par le PC-ADP, un appareil récemment développé pour recueillir des profils de vitesse simultanée avec une résolution spatiale suffisamment petite pour être applicable dans des rivières peu profondes. Une comparaison détaillée le long de deux profils verticaux des données de PC-ADP et d’ADV a toutefois illustré que les problèmes de moyennage spatial et temporel du PC-ADP n’en font pas un outil idéal pour obtenir des estimés adéquats de contrainte de cisaillement. Ces dernières sont essentielles pour mieux comprendre les liens entre la dynamique de l’écoulement des méandres et l’érosion des berges. De plus, cette étude a montré que les meilleurs estimés de contrainte de cisaillement sont obtenus par des méthodes de turbulence (Reynolds ou TKE), mais que la méthode TKE est préférable dans un contexte de méandre où la direction d’écoulement est très variable. Cette méthode requiert non seulement un volume de mesure plus petit que celui du PC-ADP, mais une plus haute fréquence d’échantillonnage. Des mesures ponctuelles avec un ADV sont donc encore essentielles pour bien caractériser la dynamique des méandres. L’idéal serait d’utiliser plusieurs ADV liés ensemble électroniquement afin d’obtenir des mesures simultanées de vitesse 3D.
Les maxima de contrainte de cisaillement mesurée avec la méthode TKE sont situés à l’entrée du méandre lorsque le niveau est plus bas, et à la sortie du méandre lorsque le niveau augmente. Ces deux zones correspondent à des observations de décrochement survenu un an après des travaux de stabilisation de berge au site d’étude. Ceci démontre la nécessité de mieux comprendre la dynamique des méandres pour mieux gérer les problèmes d’érosion et améliorer la conception des travaux futurs de stabilisation de berge.
Remerciements
Nous tenons à remercier le Fonds Québécois de la Recherche sur la Nature et les Technologies (FQRNT) pour le support financier accordé à Mike Tilston et le Conseil de Recherche en Sciences Naturelles et en Génie du Canada (CRSNG) pour le financement des travaux de terrain (Biron). Merci à Tim Haltigin, Lara Hoshizaki, Ivan Dolinsek, Bruno Vallée, Tracy LeBlanc et Lisa LeBlanc pour leur aide sur le terrain. Les commentaires de François Petit, d’un lecteur anonyme et de Hervé Piégay ont grandement contribué à améliorer le manuscrit original.
Appendices
Références
- Allen, P.M., Arnold, J. et Jakubowski, E., 1999. Prediction of stream channel erosion potential. Environmental and Engineering Geoscience, 5 : 339-351.
- Biedenharn, D.S., Elliott, C.M. et Watson, C.C., 1997. The WES Stream Investigation and Streambank Stabilization Handbook.
- Biron, P.M., Robson, C., Lapointe, M.F. et Gaskin, S.J., 2004. Comparing different methods of bed shear stress estimates in simple and complex flow fields. Earth Surface Processes and Landforms, 29 : 1403-1415.
- Blanckaert, K. et Graf, W.H., 2001. Mean flow and turbulence in open-channel bend. Journal of Hydraulic Engineering, 127 : 835-847.
- Buffin-Bélanger, T., Roy, A.G. et Kirkbride, A.D., 2000. On large-scale flow structures in a gravel-bed river. Geomorphology, 32 : 417-435.
- Chang, H., 2002. Fluvial Processes in River Engineering. Krieger Publishing.
- Clifford, N.J. et French, J.R., 1993. Monitoring and modelling turbulent flows : historical and contemporary perspectives, p. 1-34. In N.J. Clifford, J.R. French et J. Hardisty, édit., Turbulence : Perspectives on Flow and Sediment Transport. John Wiley and Sons, New York.
- Daniels, M.D. et Rhoads, B.L., 2004. Influence of large woody debris configuration on three-dimensional flow structure in two low-energy a meander bends at varying stages. Water Resources Research, 40 : W11302, 2004WR003181.
- Darby, S.E., Alabyan, A.M. et Van de Wiel, M.J., 2002. Numerical simulation of bank erosion and channel migration in meandering rivers. Water Resources Research, 38 : doi : 10.1029/2001WR000602.
- Darby, S.E. et Delbono, I., 2002. A model of equilibrium bed topography for meander bends with erodible banks. Earth Surface Processes and Landforms, 27 : 1057-1085.
- Darby, S.E. et Thorne, C.R., 1996. Stability analysis for steep, eroding, cohesive riverbanks. Journal of Hydraulic Engineering, 122 : 443-454.
- De Serres, B., Roy, A.G., Biron, P.M. et Best, J., 1999. Three-dimensional structure of flow at a confluence of river channels with discordant beds. Geomorphology, 26 : 313-335.
- Dietrich, W.E. et Smith, J.D., 1983 Influence of the point bar on flow through curved channels. Water Resources Research, 19 : 1173-1192.
- Dietrich, W.E. et Whiting, P.J., 1989. Boundary shear stress and sediment transport in river meanders of sand and gravel, p. 1-50. In River Meandering, Water Resources Monograph 12, Washington D.C.
- Dinehart, R.L. et Burau, J.R., 2005. Averaged indicators of secondary flow in repeated acoustic Doppler current profiler crossings of bends. Water Resources Research, 41 : W09405, 2005WR004050.
- Drake, T.G., Shreve, R.L., Dietrich, W.E., Whiting, P.J. et Leopold, L.B., 1988. Bedload transport of fine gravel observed by motion-picture photography. Journal of Fluid Mechanics, 192 : 193-217.
- Ferguson, R.I., Parsons, D.R., Lane, S.N. et Hardy, R.J., 2003. Flow in meander bends with recirculation at the inner bank. Water Resources Research, 39 : 1322-1335.
- Frothingham, K.M. et Rhoads, B.L., 2003. Three-dimensional flow structure and channel change in an asymmetrical compound meander loop, Embarras River, Illinois. Earth Surface Processes and Landforms, 28 : 625-644.
- Goring, D.G. et Nikora, V.I., 2002. Despiking acoustic Doppler velocimeter data. Journal of Hydraulic Engineering, 128 : 117-126.
- Heathershaw, A.D., 1979. The turbulent structure of the bottom boundary layer in a tidal current. Geophysical Journal of the Royal Astronomical Society, 58 : 395-430.
- Ikeda, S., Parker, G. et Sawai, K., 1981. Bend theory of river meanders. Journal of Fluid Mechanics, 112 : 363-377.
- Jia, Y. et Wang, S.S.Y., 1999. Numerical model for channel flow and morphological change studies. Journal of Hydraulic Engineering, 125 : 924-933.
- Johannesson, H. et Parker, G., 1989. Linear theory of river meanders, p. 181-213. In S. Ikeda et G. Parker, édit., River Meandering. Water Resources Monograph 12, Washington D.C.
- Kim, S.-C., Friedrichs, C.T., Maa, J.P.-Y. et Wright, L.D., 2000. Estimating bottom stress in tidal boundary layer from acoustic Doppler velocimeter data. Journal of Hydraulic Engineering, 126 : 399-406.
- Knighton, D., 1998. Fluvial Forms and Processes. Oxford University Press, New York.
- Lacy, J.R. et Sherwood, C.R., 2004. Accuracy of a Pulse-Coherent Acoustic Doppler Profiler in a wave-dominated flow. Journal of Atmospheric and Oceanic Technology, 21 : 1448-1461.
- Lane, S.N., Biron, P.M., Bradbrook, K.F., Butler, J.B., Chandler, J.H., Crowell, M.D., McLelland, S.J., Richards, K.S. et Roy, A.G., 1998. Three-dimensional measurement of river channel flow processes using Acoustic Doppler Velocimetry. Earth Surface Processes and Landforms, 23 : 1247-1267.
- Lane, S.N., Bradbrook, K.F., Richards, K.S., Biron, P.M. et Roy, A.G., 1999. Time-averaged flow structure in the central region of a stream confluence : a discussion. Earth Surface Processes and Landforms, 24 : 361-367.
- Lee, J.M., Nahajski, A. et Miller, S., 1997. Riverbank stabilization program. Journal of Water Resources Planning and Management, 123 : 292-294.
- McLelland, S.J. et Nicholas, A.P., 2000. A new method for evaluating errors in high-frequency ADV measurements. Hydrological Processes, 14 : 351-366.
- Mosselman, E., Shishikura, T. et Klaassen, G.J., 2000. Effect of bank stabilization on bend scour in anabranches of braided rivers. Physics and Chemistry of the Earth. Part B. Hydrology Oceans and Atmosphere, 25 : 699-704.
- Nicholas, A.P., 2001. Computational fluid dynamics modelling of boundary roughness in gravel-bed rivers : an investigation of the effects of random variability in bed elevation. Earth Surface Processes and Landforms, 26 : 345-362.
- Piégay, H., Darby, S.E., Mosselman, E. et Surian, N. 2005. A review of techniques available for delimiting the erodible river corridor : a sustainable approach to managing bank erosion. River Research and Applications, 21 : 773-789.
- Rhoads, B.L. et Kenworthy, S.T., 1998. Time-averaged flow structure in the central region of a stream confluence. Earth Surface Processes and Landforms, 23 : 171-191.
- Rhoads, B.L. et Kenworthy, S.T., 1999. Short communication : on secondary circulation, helical motion and Rozovskii-based analysis of time-averaged two-dimensional velocity fields at confluences. Earth Surface Processes and Landforms, 24 : 369-375.
- Rhoads, B.L. et Welford, M.R., 1991. Initiation of river meandering. Progress in Physical Geography, 15 : 127-156.
- Rodriguez, J.F., Bombardelli, F.A., García, M.H., Frothingham, K.M., Rhoads, B.L. et Abad, J.D., 2004. High-resolution numerical simulation of flow through a highly sinuous river reach. Water Resources Management, 18 : 177-199.
- Roy, A.G., Biron, P. et De Serres, B., 1996. On the necessity of applying a rotation to instantaneous velocity measurements in river flows. Earth Surface Processes and Landforms, 21 : 817-827.
- Roy, A.G., Biron, P.M. et Lapointe, M.F., 1997. Implications of low-pass filtering on power spectra and autocorrelation functions of turbulent velocity signals. Mathematical Geology, 29 : 653-668.
- Rüther, N. et Olsen, N.R.B., 2005. Three-dimensional modeling of sediment transport in a narrow 90° channel bend. Journal of Hydraulic Engineering, 131 : 917-920.
- Shields, F.D. Jr. et Rigby, J.R., 2005. River habitat quality from river velocities measured using Acoustic Doppler Current Profiler. Environmental Management, 36 : 565-575.
- Simon, A. et Collison, A.J.C., 2001. Pore-water pressure effects on the detachment of cohesive streambeds : seepage forces and matrix suction. Earth Surface Processes and Landforms, 26 : 1421-1442.
- Song, T. et Chiew, Y.M., 2001. Turbulence measurement in nonuniform open-channel flow using acoustic Doppler velocimeter (ADV). Journal of Engineering Mechanics, 127 : 219-232.
- Soulsby, R.L., 1980. Selecting record length and digitization rate for near-bed turbulence measurements. Journal of Physical Oceanography, 10 : 208-219.
- Soulsby, R.L., 1983. The bottom boundary-layer in shelf seas, p. 189-266. In B. Johns, édit., Physical Oceanography of Coastal and Shelf Areas. Elsevier, Amsterdam.
- Stapleton, K.R. et Huntley, D.A., 1995. Seabed stress determination using the inertial dissipation method and the turbulent kinetic energy method. Earth Surface Processes and Landforms, 20 : 807-815.
- Tilston, M., 2006. Three-dimensional flow structure, turbulence and bank erosion in a 180° meander loop. Mémoire de maîtrise, Université de Montréal, 146 p.
- Whiting, P.J. et Dietrich, W.E., 1991. Convective accelerations and boundary shear stress over a channel bar. Water Resources Research, 27 : 783-796.
- Whiting, P.J. et Dietrich, W.E., 1993. Experimental studies of bed topography and flow patterns in large-amplitude meanders : 1. Observations. Water Resources Research, 29 : 3605-3614.
- Wolf, J., 1999. The estimation of shear stresses from near-bed turbulent velocities for combined wave-current flows. Coastal Engineering, 37 : 529-543.
- Wu, W., Rodi, W. et Wenka, T., 2000. 3D numerical modelling of flow and sediment transport in open channels. Journal of Hydraulic Engineering, 126 : 4-15.
List of figures
A)
B)
(A) Vue vers l’aval de la portion amont et aval du méandre montrant des signes d’érosion. (B) Emplacement des deux profils verticaux utilisés pour la comparaison des vitesses moyennes, turbulentes et de contraintes de cisaillement entre l’ADV et le PC-ADP.
(A) Downstream view showing the upstream and downstream part of of the meander loop where bank erosion is active. (B) Position of the two vertical profiles for the comparison of mean and turbulent velocities, and bed shear stress between the ADV and PC-ADP.
A)
B)
Les différences entre les volumes de mesure des deux appareils : (A) ADV et (B) PC-ADP.
Differences in sampling volumes between the two measuring devices : (A) ADV and (B) PC-ADP.
Figure 3
Travaux de stabilisation des berges, à l’aide d’un adoucissement de la pente de la berge externe (30°) et de l’ajout de végétation, effectués en juin 2003 au site d’étude (vue vers l’aval).
Bank stabilization work, consisting in a decreased external bank slope (30°) and added vegetation, implemented in June 2003 at the field site (downstream view).
A)
B)
Comparaison des valeurs de vitesse moyenne pour les trois composantes de l’écoulement entre l’ADV et le PC-ADP dans (A) la zone centrale (position 1, fig. 1B) et (B) la zone de séparation (position 2, fig. 1B).
Comparison of mean velocity values for the three velocity components between the ADV and PC-ADP in (A) the central zone (position 1, Fig. 1B) and (B) the separation zone (position 2, Fig. 1B).
A)
B)
Comparaison des valeurs d’écart-type pour les trois composantes de l’écoulement entre l’ADV et le PC-ADP dans (A) la zone centrale (position 1, fig. 1B) et (B) la zone de séparation (position 2, fig. 1B).
Comparison of RMS values for the three velocity components between the ADV and PC-ADP in (A) the central zone (position 1, Fig. 1B) and (B) the separation zone (position 2, Fig. 1B).
A)
B)
Comparaison de différents estimés de contrainte de cisaillement dans la zone centrale (position 1, fig. 1B) pour (A) l’ADV et (B) le PC-ADP.
Comparison of bed shear stress values in the central zone (position 1, Fig. 1B) for (A) the ADV and (B) the PC-ADP.
A)
B)
Vitesse moyenne et vecteurs d’écoulement secondaire superposés, mesurés avec le PC-ADP. (A) 28 août 2003 (21 % niveau plein bord) et (B) 13 octobre 2003 (29 % niveau plein bord). Deux couleurs de vecteurs sont utilisées afin de bien les distinguer de l’arrière-plan.
colors are used for velocity vectors to distinguish them from the background color.
Mean velocity and superimposed secondary current vectors, measured with the PC-ADP. (A) August 28, 2003 (21% of bankfull discharge) and (B) October 13, 2003 (29% of bankfull discharge). Two
I
II
Intensité turbulente près de la surface pour la composante longitudinale (A), latérale (B) et verticale (C), et près du lit pour la composante longitudinale (D), latérale (E) et verticale (F) le 27 mai 2003 (I) (niveau d’eau plus bas) et le 15 mai 2003 (II) (niveau plus élevé).
Turbulence intensity near the surface for the longitudinal (A), lateral (B) and vertical (C) components, and near the bed for the longitudinal (D), lateral (E) and vertical (F) components on May 27, 2003 (I) (lower flow stage), and May 15, 2003 (II) (higher flow stage).
I
II
(A) Topographie du lit, (B) vecteurs d’écoulement moyen près du lit (flèches noires) et près de la surface (flèches grises) et (C) contrainte de cisaillement (méthode TKE) avec les contours d’élévation pour le 27 mai 2003 (I) (niveau d’eau plus bas) et le 15 mai 2003 (II) (niveau plus élevé).
(A) Bed topography, (B) mean flow vectors near the bed (black arrows) and near the water surface (grey arrows), and (C) bed shear stress (TKE method) with contour of bed topography for May 27, 2003 (I) (lower flow stage), and May 15, 2003 (II) (higher flow stage).
Figure 10
List of tables
Tableau I
Dates des campagnes d’échantillonnage et types de mesure dans chaque cas
Tableau II
Comparaison entre les pentes, les ordonnées à l’origine (régression des moindres carrés du PC-ADP en fonction de l’ADV) et les coefficients de corrélation entre l’ADV et du PC-ADP pour les moyennes et les écarts-types (RMS) dans les deux zones (centrale et de séparation)