Abstracts
Résumé
Le soutien de groupes rebelles par des États est récurrent dans les guerres civiles contemporaines. Or, souvent, ces rébellions ont relativement peu de chances de succès, même lorsqu’elles sont financées par des États puissants. Pourquoi est-ce que ceux-ci soutiennent des causes rebelles qui ont si peu de chances de réussite ? Cet article aborde ce paradoxe en suggérant que souvent les États ne cherchent pas à aider l’entreprise rebelle, mais plutôt à affaiblir un pays rival en y provoquant une guerre civile ou en intensifiant un conflit préexistant. L’analyse avec un modèle formel montre que le soutien étranger aux groupes rebelles peut agir comme une contre-force qui empêche la résolution des conflits par la voie institutionnelle. La relation historique entre la Russie et les rebelles kurdes est étudiée à la lumière des nouveaux éléments théoriques présentés.
Mots clés:
- guerre civile,
- rébellion,
- conflit international,
- démocratisation
Abstract
State sponsorship of rebel groups is a recurring phenomenon of contemporary civil wars. However, these rebellions are often relatively unlikely to succeed, even if they are financed by powerful states. Why do states support rebel causes with such limited chances of success ? This article looks into this paradox by suggesting that states often do not seek to help the rebel enterprise, but to weaken a rival country by provoking a civil war or intensifying an existing one. The analysis with a formal model shows that foreign support to rebel groups can act as a counterforce that prohibits institutional conflict resolution. The historical relationship between Russians and Turkish Kurds is analyzed with these new theoretical insights.
Keywords:
- civil war,
- rebellion,
- international conflict,
- democratization
Article body
Introduction
Depuis la Seconde Guerre mondiale, les guerres internationales directes entre États ont drastiquement diminué, tandis que les guerres par procuration (proxy wars) ont pris une nouvelle importance. Avec l’avènement de l’arme nucléaire et d’institutions internationales plus fortes et contraignantes, les États ont cherché à éviter les affrontements directs. Plusieurs pays ont donc commencé à utiliser les interventions indirectes comme substituts. Durant la guerre froide, les Soviétiques et les Américains ont chacun soutenu des groupes proches de leur idéologie dans de nombreuses guerres civiles (Mumford 2013). Plus récemment, le conflit entre l’Iran et l’Arabie Saoudite s’est immiscé dans plusieurs conflits civils au Moyen-Orient, tels que le conflit syrien actuel (Gause 2014).
Contrairement aux États qui, pour la plupart, ont de nombreuses relations commerciales et diplomatiques à préserver, les groupes rebelles n’ont pas autant besoin de maintenir leur légitimité face à la communauté internationale. De plus, même si le financement de ces groupes est souvent illégal ou à tout le moins condamné par les autres États, il est difficile à détecter et généralement encore plus difficile à démontrer. Il est donc devenu une façon efficace de contourner les obstacles légaux et diplomatiques aux interventions militaires (Salehyan 2010) et d’éviter l’escalade vers la nucléarisation des conflits (Mumford 2013). Aujourd’hui encore, ces alliances sont récurrentes. Parmi les cas les plus récents figurent l’Iran et le Hezbollah (Kamel 2017), le Soudan et les rebelles au Tchad (San-Akca 2016), ainsi que la Russie et les rebelles kurdes en Syrie et en Turquie (Kamel 2017 ; Reynold 2016).
Plusieurs raisons peuvent expliquer le soutien étatique à des groupes rebelles. Entre autres, les États soutiennent parfois des rébellions de groupes minoritaires dans des pays voisins car ils partagent des liens ethniques, religieux ou idéologiques forts avec ceux-ci. Cependant, dans de nombreux cas, les rebelles et leurs bienfaiteurs ont bien peu en commun, que ce soit culturellement ou idéologiquement (San-Akca 2016). De surcroît, il semble que les groupes rebelles aient souvent au départ des chances marginales d’arriver à leurs fins. À cela s’ajoute un soutien étranger fréquemment insuffisant pour donner une chance de réussite considérable à leur entreprise. Le cas du soutien russe aux rebelles kurdes en Turquie est particulièrement parlant. Les Russes ont peu en commun avec les Kurdes du point de vue culturel ou idéologique, mais cela fait tout de même près de deux siècles qu’ils soutiennent ces derniers. Cependant cet appui n’a jamais été suffisamment fort pour permettre aux Kurdes d’obtenir, ni en totalité ni en partie, leur autonomie tant souhaitée. Cela suggère qu’elle n’a jamais été au coeur des préoccupations russes (Reynold 2016). Pourquoi les États financent-ils donc des rébellions qui ont relativement peu de chances de succès ?
La réponse qu’apporte cet article est que l’objectif véritable des États est souvent d’affaiblir un pays en y changeant les rapports de pouvoir entre un groupe rebelle et le gouvernement. Ils peuvent ainsi favoriser les rébellions et nuire à l’unité nationale. Puisque le soutien de groupes rebelles coûte généralement peu sur les plans politiques et financiers, il s’agit donc d’une façon efficiente d’affaiblir un adversaire (Salehyan et al. 2011), ce qui peut servir plusieurs objectifs.
En particulier, un pays peut vouloir maintenir une position de domination sur un autre ou s’assurer une protection face à lui ou à ses alliés (Waltz 2010). Il s’agit par exemple d’une façon d’expliquer le soutien des pays musulmans du Moyen-Orient aux groupes armés pro-Palestine dans le conflit israélo-palestinien. En effet, ces pays craignent une trop grande montée en puissance d’Israël. Celle-ci représente d’autant plus une menace qu’elle ouvre la porte à une plus grande influence des Américains qui entretiennent des différends avec plusieurs pays de la région (citons notamment l’opposition États-Unis-Iran). Les groupes rebelles palestiniens peuvent ainsi être instrumentalisés pour affaiblir Israël et empêcher sa montée en puissance (San-Akca 2016).
Affaiblir un autre pays peut aussi permettre d’avoir un avantage dans un conflit international. Mentionnons pour exemple le soutien des services secrets pakistanais aux rebelles du Cachemire et du Jammu, qui ont longtemps entretenu une guerre extrêmement coûteuse pour l’Inde. Or celle-ci avait peu de chances dans les faits de mener à une sécession (Roberts 2008). Encore une fois, le financement était juste suffisant pour favoriser un long conflit civil dommageable pour l’Inde sans donner une trop bonne chance de victoire aux rebelles. Cela suggère que le Pakistan cherchait principalement à « entretenir le feu »[1] pour affaiblir l’Inde dans la région plutôt qu’à aider les minorités musulmanes du pays. Ce soutien continu, bien que coûteux, a pu aider grandement le Pakistan dans les guerres de 1947, 1965, 1971 et 1999 et lors de ses nombreux autres différends avec l’Inde (Paul 2005).
Finalement, cela peut aussi faciliter le maintien d’une position avantageuse dans une négociation pour un enjeu régional. En effet, selon l’approche réaliste des relations internationales, celles-ci sont influencées par l’équilibre des pouvoirs entre les pays, même en période de paix (Waltz 2010). En soutenant une rébellion, un État peut affaiblir un adversaire et ainsi modifier l’équilibre du pouvoir à son avantage. Cela peut expliquer pourquoi l’Afrique du Sud de l’apartheid a grandement soutenu des milices luttant contre les gouvernements de pays voisins tels que le Zimbabwe. Les régimes visés étaient généralement fortement opposés au pouvoir des minorités blanches en Afrique, et l’Afrique du Sud a pu chercher ainsi à protéger les politiques pro-blanches de la région (Frankel 1984).
Dans cet article, je propose un modèle formel pour étudier ce phénomène et mieux comprendre le rôle du soutien étatique aux groupes rebelles dans la dynamique des guerres civiles. Ce modèle permet de comprendre comment le soutien étatique interagit avec d’autres variables qui influencent la prépondérance et l’intensité des guerres civiles, notamment le rapport de force entre un gouvernement et les groupes rebelles dans son pays, de même que la capacité des institutions démocratiques et légales à répondre de façon crédible aux demandes politiques et économiques des minorités.
Le modèle prend la forme d’un jeu en information complète à trois étapes où interagissent trois acteurs : un groupe rebelle, le gouvernement et un État étranger. Premièrement, l’État étranger choisit l’ampleur de son soutien au groupe rebelle en cas de conflit. Deuxièmement, le groupe rebelle décide de combattre le gouvernement avec le soutien étranger ou conserve le transfert économique qui lui est offert en échange de la paix. Finalement, s’il y a un conflit, le gouvernement et le groupe rebelle choisissent leurs investissements dans le conflit.
De l’analyse de cette dynamique ressort un paradoxe : l’amélioration des institutions démocratiques et légales d’un pays peut conduire à une intensification des guerres civiles. En effet, la plupart de ces guerres ont lieu dans des pays partiellement démocratiques où les minorités ne sont pas bien intégrées politiquement et économiquement, ce qui suggère une corrélation négative avec la qualité des institutions. Or, une amélioration des institutions peut aussi empirer les conflits dans certaines situations. Si un gouvernement étranger a avantage à ce que le pays soit faible, une amélioration institutionnelle favorisant l’intégration pacifique des minorités dissidentes peut encourager un plus grand soutien aux factions rebelles. Cela peut aussi être le cas lorsque l’État étranger a certaines autres motivations (voir annexe 3). L’État étranger peut ainsi éviter que les rebelles soient pacifiés en leur offrant une meilleure chance d’obtenir ce qu’ils désirent par la voie du conflit. La simple possibilité du financement étranger ouvre donc une trappe qui empêche les pays de mettre fin aux guerres civiles pacifiquement. Ce résultat est suggéré par l’analyse de plusieurs études de cas. Notamment, celle de la première guerre du Congo, qui a eu lieu à la suite de l’abolition de la politique du parti unique de Mobutu, qui a constitué une évolution démocratique notoire. De nombreux adversaires de ce régime, incluant le Rwanda, l’Ouganda, le Burundi et l’Angola, ont accru leur soutien aux rebelles du pays (Tamm 2016), possiblement pour parer à la possibilité que le Congo puisse un jour être en mesure de pacifier ses groupes rebelles. S’ajoutent à cela les nombreux cas de guerres civiles qui se sont déclenchées après l’indépendance et la démocratisation d’anciennes colonies. Dans plusieurs de ces guerres, des États antagonistes ont soutenu les groupes rebelles opposés aux gouvernements. Citons notamment le cas du soutien sud-africain aux rebelles du Zimbabwe et de l’Angola (Frankel 1984), ainsi que le soutien pakistanais aux rebelles des provinces indiennes du Cachemire et du Jammu (Roberts 2008).
Cet article est structuré de la façon suivante : la prochaine section traite des travaux sur le sujet ; la section II présente le modèle, en commençant par les hypothèses et la chronologie adoptée, suivie de sa résolution détaillée. La section III porte sur l’effet de trappe du financement étranger de groupes rebelles, avant la conclusion puis les annexes explicatives.
I – Revue des travaux pertinents
A – Motivations
Le soutien à des groupes rebelles fait partie d’un ensemble de mesures que peuvent adopter les États pour intervenir militairement dans d’autres pays. La première et la plus évidente est l’intervention directe, qui s’avère cependant extrêmement risquée et coûteuse sur les plans économique et politique (Salehyan et al. 2011), ce qui encourage les États à plutôt recourir à des agents locaux. Ceux-ci peuvent servir plusieurs objectifs. Ils peuvent être utilisés par des États pour exploiter des ressources, bien que cela soit rare étant donné le coût de financement de telles opérations sur une période prolongée (Bernauer 2016). En soutenant un groupe rebelle, un État étranger peut aussi chercher à aider un groupe avec lequel il partage des liens ethniques, religieux ou idéologiques (Gleditsch 2017 ; Bernauer 2016 ; San-Akca 2016). Un État peut aussi vouloir mettre en place des régimes facilement manipulables afin de s’assurer qu’ils adoptent des politiques économiques ou militaires qui lui soient favorables (Padró i Miquel et Yared 2012). De plus, un pays peut être encouragé à mettre en place un régime vassal afin d’empêcher d’autres puissances d’y étendre leur influence (Berman et Lake 2019). Enfin, le financement de rébellions peut être un moyen de pression efficace lors de négociations internationales (Maoz et San-Akca 2012).
Dans cet article, je me concentre cependant sur une autre motivation pour le soutien à des groupes rebelles : la déstabilisation d’un pays rival (San-Akca 2016 ; Salehyan et al. 2011 ; Lee 2018). Ce type de déstabilisation peut avoir un impact énorme sur les systèmes politiques et économiques d’un adversaire, permettant ainsi de maintenir une position de domination qui protège d’une agression, facilite la victoire en cas de guerre ou aide lors de négociations pour un enjeu régional. Cette stratégie est rarement ouvertement admise par ses instigateurs, mais tout porte à croire qu’elle est communément employée (Salehyan et al. 2011 ; San-Akca 2016).
B – Dynamique des conflits avec soutien étatique à des groupes rebelles
Lorsqu’un État étranger soutient un groupe rebelle, cela peut changer radicalement la dynamique d’une guerre civile. Celle-ci risque en effet d’être plus longue et difficile à résoudre par la négociation (Cunningham 2010 ; Akcinaroglu et Radziszewski 2005 ; Sawyer et al. 2017 ; Konyukhovskiy et Grigoriadis 2019), ainsi que plus intense et violente (Nedrebo 2009 ; Martinez 2017).
La simple possibilité qu’un groupe rebelle puisse être soutenu par un État étranger, comme lorsqu’il y a un lien ethnique ou religieux, peut avoir un impact important sur la dynamique politique d’un pays. Cela peut favoriser les conflits civils (Cederman et al. 2013 ; van Houten 1998), la discrimination économique des minorités, de même que l’exclusion politique et l’assimilation (Michalopoulos et Papaioannou 2016 ; Jenne 2004). Ces liens peuvent aussi encourager le sous-investissement dans les institutions démocratiques, légales et de gouvernance dans les régions habitées par ces groupes minoritaires (Lee 2018).
C – Modèles existants
Le modèle classique de délégation se prête particulièrement bien à l’analyse du soutien étatique à des groupes rebelles. En effet, plusieurs auteurs adaptent ce modèle à cette problématique (Bapat 2012 ; Salehyan 2010 ; Salehyan et al. 2014 ; Salehyan et al. 2011 ; Konyukhovskiy et Grigoriadis 2019). D’autres développent de nouveaux modèles pour analyser comment le soutien étranger de rebelles peut encourager la violence envers les civils (Salehyan et al. 2014), comment le potentiel d’obtenir ce soutien peut encourager un groupe ethnique à se rebeller (Sambanis et al. 2018) et comment cela peut changer la façon dont il est traité par son gouvernement (van Houten 1998).
Ainsi, bien que ces modèles permettent de mieux comprendre la dynamique des relations rebelles-mécènes et rebelles-gouvernement, ils mettent un peu de côté la dynamique tout aussi complexe des conflits internationaux sous-jacents. Ceux-ci sont néanmoins pris en compte dans le modèle de Schultz (2010), qui voit dans le soutien apporté à des groupes rebelles une façon d’attaquer un adversaire de façon secrète, ce qui peut provoquer l’échec de négociations internationales. De même, de façon plus minimaliste, Maoz et San-Akca (2012) modélisent la décision des États d’utiliser des groupes non étatiques pour s’attaquer mutuellement, et la façon dont ils sont influencés par les possibilités de représailles. Bagchi et al. (2019), quant à eux, mettent en place un modèle avec trois États étrangers représentatifs de la guerre en Syrie.
Cependant ces modèles ignorent l’importance des institutions politiques dans l’émergence des guerres civiles. D’un autre côté, certains récents modèles économiques de guerres civiles (Azam 2006 ; Besley et Persson 2011) prennent en compte cette dimension fondamentale, mais ne considèrent pas l’impact du financement des groupes rebelles par d’autres pays[2]. Or, lorsqu’on ajoute cet aspect, cela transforme profondément la dynamique de ces modèles économiques. Le modèle que je développe dans la section qui suit est donc inspiré de ces deux modèles et permet de réunir les idées les plus importantes de ces deux branches des travaux de recherche dans un même cadre théorique.
D – Institutions et conflits
L’effet de trappe, qui est analysé à l’aide du modèle en section III, porte sur les liens entre la capacité des institutions démocratiques et légales d’inclure et protéger les minorités, et les guerres civiles. Ces liens ont été largement étudiés dans les travaux en science politique. En général, plus les régimes ont des institutions fortes, plus ils sont préservés du risque de guerre civile (voir Hegre 2014 pour une revue des travaux). Néanmoins, il reste que les régimes les plus fortement autocratiques sont plus stables que les régimes intermédiaires, selon Hegre et al. (2001). L’explication est que, d’un côté, les démocraties les plus avancées ont des institutions fiables qui permettent aux gouvernements de partager le pouvoir politique et économique avec les minorités de façon crédible et durable. Ces minorités sont donc satisfaites sur le plan économique et peuvent aborder leurs problèmes avec le gouvernement de façon démocratique et non violente. D’un autre côté, les régimes les plus autoritaires présentent une forte concentration des pouvoirs politiques, économiques et militaires, ce qui rend les rébellions presque impossibles. En particulier, il est beaucoup plus facile pour les régimes autoritaires de réprimer sévèrement les minorités dissidentes. Ce sont donc les régimes qui ne sont pas pleinement démocratiques, mais qui n’ont pas non plus un État tout puissant, qui sont les plus susceptibles de connaître des conflits armés internes.
Néanmoins, une transition démocratique au sein même d’un pays peut aussi avoir un impact important à court terme. Plusieurs études ont montré que les améliorations sur le plan démocratique peuvent favoriser l’émergence de guerres civiles particulièrement virulentes (Gleditsch 2009 ; Cederman et al. 2010)[3], ce qui avait été suggéré entre autres par Huntington (1993). Les périodes de démocratisation (et d’autocratisation) sont souvent des périodes d’instabilité politique qui peuvent mener à des conflits civils. Or, aucune théorie jusqu’à présent n’a abordé l’impact des acteurs internationaux sur la relation entre la démocratisation et les guerres civiles. Cet article permet donc d’aborder cette question sous un nouvel angle.
II – Modèle
A – Hypothèses
Je considère un jeu dynamique en information complète. Il y a trois acteurs : un groupe rebelle (O), un gouvernement (I) et un État étranger (E). En début de jeu, le gouvernement contrôle des ressources disputées (R > 0), qui peuvent être nationales ou régionales, comme lors d’une guerre d’indépendance. Les rebelles quant à eux contrôlent des ressources normalisées à zéro par simplicité. Il y a deux situations possibles : soit les rebelles décident de se rebeller, auquel cas il y a une guerre civile, soit la paix est maintenue.
Dans le cas d’une rébellion, je modélise le conflit civil avec un tournoi de Tullock sous une forme simple (Hirshleifer et Osborne 2001 ; Grossman et Kim 1995). Il est très commun dans les travaux en économie sur les guerres civiles d’utiliser ce type de modélisation (voir Skaperdas 1996 ; Pietri 2017). Dans ce jeu, la probabilité de victoire des rebelles est :
Dans cette équation, est un indicateur de l’avantage relatif des rebelles lors d’un
conflit militaire avec le gouvernement. ![]() correspond à l’absence d’un avantage relatif pour l’une des parties et plus
α est faible, plus le gouvernement est avantagé. LO et LI représentent respectivement les investissements dans le conflit des
forces rebelles et gouvernementales. Les deux groupes peuvent investir à un coût constant
et égal à 1.
correspond à l’absence d’un avantage relatif pour l’une des parties et plus
α est faible, plus le gouvernement est avantagé. LO et LI représentent respectivement les investissements dans le conflit des
forces rebelles et gouvernementales. Les deux groupes peuvent investir à un coût constant
et égal à 1.
Cette fonction de conflit est construite à partir de plusieurs hypothèses implicites. Entre autres, je suppose que les parties en présence ont réglé leurs problèmes d’actions collectives et de recrutement, qu’elles sont neutres par rapport au risque (voir ci-dessous) et que leurs investissements dans le conflit, qu’ils soient financiers, matériels ou humains (risque de mort, impact psychologique, etc.), font tous partie de L. Il s’agit d’hypothèses simplificatrices communément faites dans les travaux portant sur les conflits[4]. De plus, elles ont un rôle négligeable dans le mécanisme que j’étudie ici et n’affectent pas le résultat principal.
Dans le cas d’une guerre, les deux parties cherchent à maximiser leur gain espéré qui prend la forme suivante :

LI et LO représentent donc de façon endogène les pertes bilatérales causées par une guerre civile. Ces investissements sont en effet perdus lors d’un conflit au lieu d’être utilisés pour des activités productives. En effet, les ressources totales passent de R à R − LI − LO.
Deux facteurs peuvent décourager le groupe rebelle d’entrer en conflit : un avantage militaire (α ) trop faible et un partage de la rente économique (T) en période de paix assez généreux. Ce dernier est directement dépendant des institutions politiques et légales du pays. Celles-ci jouent un rôle important pour prévenir les guerres civiles en assurant aux groupes minoritaires qu’ils peuvent être représentés politiquement et recevoir une part suffisante de la rente économique en période de paix. Dans le modèle d’Azam (2006), la qualité des institutions est vue comme déterminant la capacité du gouvernement de faire des promesses de façon crédible ; cela prend la forme de la probabilité de réalisation du transfert promis après que l’occasion de se rebeller soit passée. Pour illustrer le mécanisme causal qui m’intéresse ici, je peux me contenter d’une modélisation encore plus simple, analogue à celle de Besley et Persson (2011) : en période de paix, le groupe d’opposition reçoit un partage de la rente fixe T[5]. Ainsi, lorsque la possibilité d’une révolte est passée, ce sont les contre-pouvoirs et les institutions démocratiques et légales qui empêchent le groupe au pouvoir de s’approprier l’entièreté des ressources et non pas la menace d’insurrection. Par simplicité, j’émets l’hypothèse que la concession du gouvernement est économique, mais un modèle strictement équivalent pourrait intégrer une concession sur le plan politique (au niveau de l’alignement gauche-droite par exemple) ou culturel (au niveau de l’importance politique de différentes religions par exemple).
Dans les pays démocratiques où l’État de droit domine, les minorités sont généralement mieux représentées politiquement[6]. Leur pouvoir politique et leurs ressources économiques sont plus enclins à être proportionnels à ceux de la majorité. Elles ont donc beaucoup plus à perdre à entrer en conflit avec le gouvernement, ce qui explique que les rébellions soient plus rares dans les États les plus démocratiques (Besley et Persson 2011).
L’État étranger (E) a quant à lui un rôle et un objectif différents des autres joueurs. Il existe plusieurs raisons qui peuvent motiver cet État à financer un groupe rebelle[7], mais je m’intéresse ici plus particulièrement à la situation où il le fait dans le but d’affaiblir un pays ennemi. Dans ce cas, il est indifférent de savoir qui prend le pouvoir à la fin du jeu, que ce soit le gouvernement (I) ou ses opposants (O). Ainsi, dans ce modèle, l’État étranger (E) retire un gain lorsque les ressources totales du pays sont réduites par une guerre civile à cause des pertes du gouvernement (LI) et des rebelles (LO). En réduisant les ressources du pays, l’État étranger diminue la capacité de sa cible à se défendre ou à attaquer, et ce peu importe qui prend le pouvoir. Il ne se soucie donc guère de l’issue du conflit.
Définition 1. P représente les capacités du pays à la fin du jeu, évaluées comme étant les ressources totales en fin de jeu (P = R − LI − LO).
Les capacités du pays (P) sont un élément important du point de vue des relations internationales. En effet, un gouvernement ayant de plus grandes capacités (contrôlant plus de ressources) sera davantage en mesure de défendre ses intérêts face aux autres pays. Il s’agit donc d’un élément déterminant de la notion de puissance, qui est un aspect fondamental des relations internationales selon l’approche réaliste (Waltz 2010).
Je considère une forme réduite simple ( f ) pour représenter l’utilité de l’État étranger en fonction des capacités du pays.
Hypothèse 1. f est deux fois dérivable de même que décroissante et concave en fonction de P[8].
Je pose ainsi l’hypothèse intuitive que l’État étranger retire un gain positif de l’affaiblissement du pays, ce qui est généralement le cas lorsque les deux sont des adversaires sur la scène internationale. La concavité vient du fait que, généralement, l’État étranger retire un gain très important si l’un de ses adversaires est affaibli, mais de moins en moins important s’il est affaibli davantage. Par exemple, si l’État étranger cherche à se protéger d’une agression du pays adverse ou à s’imposer lors de négociations pour un enjeu régional, plus l’autre pays est faible, moins il représente un problème réel et moins il est important de l’affaiblir encore plus. Cette propriété ressort d’ailleurs de façon endogène dans des modèles économiques de conflits et plus particulièrement dans la fonction de conflit de Skaperdas (1992).
Je considère que l’État étranger (E) peut investir s à un coût croissant et convexe (ou linéaire)
C(s) pour améliorer l’avantage comparatif des rebelles dans une guerre civile contre le gouvernement. Cette fonction de coût inclut les dépenses concrètes (armes, soutien logistique, etc.), mais aussi les coûts d’auditoires (audience costs) envers la population de l’État étranger et la communauté internationale (Salehyan 2010). Cela peut expliquer pourquoi les pays autoritaires tels que la Russie sont davantage susceptibles de soutenir des groupes rebelles : pour eux, le coût d’un contrôle national et international est plus faible (Karlén 2019).
Ainsi, le paramètre α étudié précédemment peut être décomposé en deux parties (α =
α0 + s) où α =
α0 représente l’avantage initial des rebelles sans l’aide d’un État
étranger et s ∈ [0,1 − α0) est
le soutien étranger. J’émets l’hypothèse que le groupe rebelle n’a jamais un avantage
initial sur le gouvernement ![]() [9]. Néanmoins, dans de nombreux cas, le
gouvernement peut recevoir lui aussi une aide extérieure substantielle dans le but de
l’aider à garder le contrôle de son pays. Dans le contexte de ce modèle, cette aide
contribuerait à augmenter l’avantage initial du gouvernement (α0 serait
plus petit).
[9]. Néanmoins, dans de nombreux cas, le
gouvernement peut recevoir lui aussi une aide extérieure substantielle dans le but de
l’aider à garder le contrôle de son pays. Dans le contexte de ce modèle, cette aide
contribuerait à augmenter l’avantage initial du gouvernement (α0 serait
plus petit).
L’un des éléments importants dans les travaux en science politique est la complémentarité des ressources et des savoirs entre les groupes rebelles et leurs financeurs étrangers (Salehyan et al. 2011 ; San-Akca 2016). Pour un État, le coût d’envoyer des soldats dans un autre pays est très élevé, ne serait-ce que du point de vue politique (Mumford 2013). Les rebelles quant à eux ont souvent beaucoup plus de facilité à recruter des soldats, car ils peuvent le faire au sein de bassins démographiques souvent pauvres, où les gens sont parfois sympathisants de leur cause ou prêts à risquer leur vie à moindre coût. Ces groupes ont cependant beaucoup de difficulté à acquérir du capital financier et du matériel militaire, car ils agissent dans l’illégalité et doivent acquérir ces biens dans l’ombre du gouvernement. La complémentarité entre l’État étranger et le groupe rebelle peut donc être due à l’asymétrie des coûts du capital et du recrutement de soldats entre les deux acteurs (Salehyan et al. 2011).
Ainsi, une façon d’analyser α est de le voir comme le stock relatif de capital physique qui est complémentaire du capital humain (soldats). Il peut s’agir d’armement, de stratèges militaires compétents, de défenses, etc. α dépend donc du ratio entre le capital des rebelles et celui du gouvernement. La convexité ou la constance du coût de s pour améliorer ce ratio à l’avantage des rebelles est donc facilement justifiable si on suppose un coût constant ou convexe pour augmenter le capital des rebelles (voir l’annexe 2 pour une justification mathématique).
Cette modélisation simple de l’avantage relatif des rebelles a de nombreux avantages. Non seulement elle permet de simplifier la résolution et l’analyse du modèle, mais elle permet aussi de rendre compte de plusieurs aspects importants de la collaboration entre les États étrangers et les groupes rebelles. En effet, la complémentarité peut prendre plusieurs formes et le paramètre s peut représenter bien plus que l’armement ou le capital physique. Les financeurs étrangers peuvent mettre en place des camps d’entraînement sur leur territoire pour les groupes rebelles qu’ils soutiennent (San-Akca 2016 ; Salehyan et al. 2011). Les rebelles ont aussi généralement une compréhension du terrain plus approfondie qui complémente l’expertise militaire de leur investisseur. De plus, ils ont souvent un soutien populaire qui facilite les opérations militaires, et un financeur étranger puissant peut renforcer leur crédibilité face à la population (Salehyan et al. 2011).
B – Chronologie
Le jeu se déroule en trois étapes. Dans un premier temps, l’État étranger (E) choisit son niveau de soutien s et paye C(s). Le groupe rebelle (O) décide ensuite s’il s’engage dans un conflit (L0 > 0) ou pas (L0 = 0). Dans un tel cas, il reçoit le transfert qu’il obtient toujours en temps de paix et le jeu se termine. Le gouvernement (I) obtient R − T, les rebelles (O)T et l’État étranger (E) a une utilité de f (R) – C(s). Cependant, si les rebelles se révoltent, ils abandonnent le transfert T et ils entrent dans un tournoi de Tullock avec le gouvernement tel que décrit précédemment. Les deux joueurs maximisent leur gain espéré et les allocations LO et LI sont déterminées par un équilibre de Nash unique. Le gagnant est décidé avec une probabilité endogène au tournoi de Tullock et le jeu se termine. Dans cette situation, le gain espéré du gouvernement est (1 − (α0 + s))2R, celui du groupe rebelle est (α0 + s)2R et le gouvernement étranger retire une utilité de f (P) − C(s) (P = R − LI − LO). Le jeu est ainsi illustré :

La chronologie du jeu à partir de la seconde étape est particulièrement proche du modèle d’Azam (2006), et très similaire à ce qui est généralement considéré dans les travaux sur les guerres civiles dans lesquels presque tous les modèles (voir entre autres Fearon 2004 ; Besley et Persson 2011 ; van Houten 1998) voient les rebelles (O) accepter ou refuser des ressources en échange de la paix. S’ils refusent, ils peuvent alors tenter de renverser le gouvernement[10].
L’État étranger joue avant le groupe d’opposition dans le modèle. D’une part, il est logique de laisser au groupe rebelle le dernier mot dans la décision de provoquer un conflit ou non. Après tout, c’est lui qui mènera directement un tel conflit et non l’État étranger qui occupe plutôt un rôle de soutien. D’autre part, la négociation entre le groupe rebelle et l’État étranger est hautement asymétrique. Ce dernier est beaucoup plus puissant, ce qui le place dans une position de domination lors d’une négociation avec le groupe rebelle. De plus, la rébellion est généralement bien moins importante pour l’État étranger que pour le groupe d’opposition local : le soutien à une rébellion n’est qu’une stratégie parmi d’autres pour l’État étranger, tandis qu’il s’agit souvent de la raison d’être du groupe rebelle. L’impact de l’échec de la négociation est donc bien moins important pour l’État étranger que pour les rebelles. Les modèles de négociation tels que celui de Nash (Binmore et al. 1986) prédisent qu’avec une telle asymétrie, l’un des deux acteurs, ici l’État étranger, a essentiellement un avantage équivalent à jouer en premier[11].
C – Résolution
Le jeu se résout par raisonnement inversé (backward induction).
Étape 3. Je considère le cas où il y a une guerre civile. L’équilibre de Nash pour ce tournoi de Tullock est L*I = L*O = (α0 + s)(1 - (α0 + s))R (Hirshleifer et Osborne 2001). À l’équilibre, les gains espérés des deux joueurs dans ce sous-jeu sont :

Étape 2. Le groupe rebelle (O) a le choix entre se rebeller (LO > 0) et obtenir un gain espéré de (α0 + s)2R ou ne pas se révolter (LO = 0) et obtenir T, le transfert gouvernemental. Par conséquent, il se rebelle si (α0 + s)2R ≥ T[12].
Étape 1. Je considère que l’État étranger (E) retire une utilité en fonction des capacités en fin de jeu du pays qui respecte l’hypothèse 1. Celui-ci cherche à maximiser son gain espéré.
Proposition 1. Définissons g(s) = f(Pα0 + s) - C(s), le gain que l’État étranger cherche à optimiser et
s* comme
sa stratégie optimale.s* = 0 si pour
tout ![]() , . Sinon, s* se trouve dans la partie
concave de g et il y a deux possibilités :
, . Sinon, s* se trouve dans la partie
concave de g et il y a deux possibilités :
a)![]() ou g est décroissant sur
l’intervalle
ou g est décroissant sur
l’intervalle
![]()
Dans ce cas, ![]() .
.
b) il existe ![]() tel que g'(ŝ). Dans ce cas, s* = ŝ.
tel que g'(ŝ). Dans ce cas, s* = ŝ.
Nous pouvons représenter graphiquement ce problème d’optimisation[13].
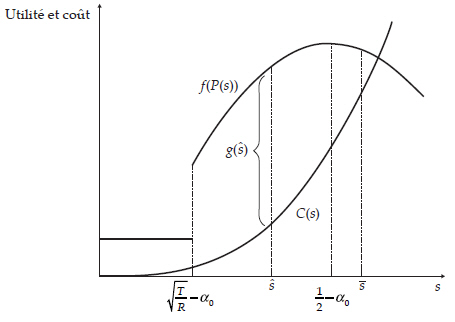
Figure 1
Problème d’optimisation de l’État étranger (E)
Lorsque s* = 0, cela signifie que soutenir
le groupe rebelle est trop coûteux pour l’État étranger comparativement à ce qu’il peut en
retirer. Il va donc s’abstenir de le faire. Si ![]() (cas a), alors l’État étranger va financer la rébellion, mais juste
suffisamment pour qu’elle ait lieu. Il donne par conséquent une chance de victoire
minimale au groupe rebelle. À l’opposé, si
(cas a), alors l’État étranger va financer la rébellion, mais juste
suffisamment pour qu’elle ait lieu. Il donne par conséquent une chance de victoire
minimale au groupe rebelle. À l’opposé, si ![]() (cas b), l’État finance le groupe rebelle au-delà de ce qui est strictement
nécessaire pour déclencher une rébellion, car il veut accroître l’intensité du
conflit.
(cas b), l’État finance le groupe rebelle au-delà de ce qui est strictement
nécessaire pour déclencher une rébellion, car il veut accroître l’intensité du
conflit.
Nous avons donc toutes les valeurs à l’équilibre du jeu, ce qui complète la résolution.
III – L’effet de trappe
Dans cette section, j’étudie le résultat le plus important du modèle. Je commence par définir une valeur endogène au modèle qui permet d’alléger l’énoncé de la prochaine proposition.
Définition 2.s̅ est le plus grand investissement que l’État étranger (E) est prêt à faire pour améliorer l’avantage comparatif du groupe rebelle (O), pour des α0 et R donnés et pour tout T. Formellement, s̅:= sup{s} tel que f(P(α0 + s)) - C(s) ≥ f(P(α0)) - C(0), le gain obtenu par l’État étranger lorsque s = 0[14].
Proposition 2. Considérons le choix optimal du soutien étranger (s*) en fonction du paramètre T et pour tous les autres paramètres fixés. Il y a trois possibilités :
a)s* est constant et égal à ŝ (tel que défini en proposition 2) si T < (α0 + ŝ)2R
b) s* est constant et égal à 0 si T > (α0 + s̅)2R.
c) ![]() si T ∈[ (α0 +
ŝ)2R, α0 + s̅)2R] et donc une augmentation de T à l’intérieur de cet intervalle augmente s*.
si T ∈[ (α0 +
ŝ)2R, α0 + s̅)2R] et donc une augmentation de T à l’intérieur de cet intervalle augmente s*.
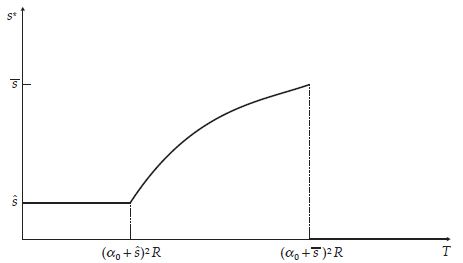
Figure 2
Soutien au groupe rebelle en fonction des institutions du pays
Les institutions du pays génèrent une contrainte d’incitation pour l’État étranger lorsqu’il veut amener le groupe rebelle à prendre les armes contre son gouvernement. Dans le cas a), cette contrainte est inactive et une variation dans la qualité des institutions n’affecte pas le soutien étranger, puisque ce dernier est prêt à investir plus que ce qui est nécessaire pour respecter cette contrainte. Cela peut correspondre à un investissement nul si l’avantage initial du groupe rebelle est assez élevé. Dans le cas b), il est trop coûteux de soutenir le groupe rebelle, car la contrainte d’incitation est trop élevée. L’État étranger s’abstient donc de le faire. Enfin, dans le cas c), la contrainte d’incitation est active, mais n’est pas assez élevée pour décourager l’investissement étranger. Une amélioration des institutions conduit donc l’État à offrir davantage de soutien au groupe rebelle, car cela est nécessaire pour que ce dernier ne fasse pas la paix avec son gouvernement. Puisqu’ils reçoivent plus de soutien extérieur et que ce soutien est complémentaire à leurs propres efforts, les rebelles sont encouragés à intensifier leurs actions militaires[15].
Ainsi, le soutien étranger peut agir comme une contre-force lorsqu’un pays améliore ses institutions, en particulier lorsque cela favorise l’inclusion économique et politique du groupe minoritaire. Par exemple, un pays qui serait en voie de développer des systèmes démocratiques et légaux de plus grande qualité pourrait voir un groupe rebelle dans son pays recevoir plus de financement de la part d’un État étranger. Ce dernier pourrait ainsi s’assurer que les rebelles continueront de se révolter, ce qui maintiendra le pays dans un état d’affaiblissement malgré l’amélioration de ses institutions. Pour qu’un pays se libère du risque de guerre civile, il faut donc que ces dernières s’améliorent jusqu’à atteindre un certain seuil. Il est donc important que la communauté internationale soit consciente qu’une faible amélioration des institutions dans un pays peut être inefficace. En effet, cela peut entraîner une augmentation du financement étranger aux rebelles, ce qui peut intensifier le conflit. Seule une amélioration d’une importance significative peut sortir un pays de cette trappe générée par le soutien extérieur aux groupes rebelles. Cette augmentation doit en général être encore plus importante si le pays financeur a un régime politique autoritaire. En effet, un pays tel que la Russie a des coûts d’auditoires faibles, et il est donc encore plus difficile de le décourager de soutenir une rébellion.
Pour qu’il y ait un effet de trappe, il faut que l’avantage initial des opposants ne soit pas trop faible. Or, lorsque le gouvernement reçoit déjà un soutien extérieur considérable visant à l’aider à garder le contrôle du pays, ce qui est relativement souvent le cas, les rebelles commencent généralement avec un avantage presque nul. Par exemple, le Rwanda a reçu un soutien international abondant depuis la fin du génocide de 1994, ce qui a contribué à la stabilisation politique du pays (The Economist 2016). Étant donné que le pays a des adversaires potentiels (rdc, Ouganda, etc.) et des tensions internes sous-jacentes qui pourraient être exploitées par ceux-ci, on peut penser que c’est le soutien important que le gouvernement reçoit qui le protège de la déstabilisation et donc de l’effet de trappe.
L’effet de trappe peut aussi être observé lorsque l’État étranger a d’autres motivations : il peut se soucier uniquement de la perte du côté gouvernemental (LI) ou peut chercher à générer de la destruction en plus des pertes dues aux investissements dans le conflit ; il peut aussi chercher à mettre le groupe rebelle au pouvoir, mais il est important qu’il ne retire pas de gain si le gouvernement du pays confronté aux rebelles lui fait des concessions sur les plans politique ou économique. Dans le cas contraire, l’effet de trappe ne devrait pas être observé. En annexe 3, je discute plus en détail de la façon dont ces autres hypothèses sur les motivations de l’État étranger affectent le modèle et les résultats, et je montre pourquoi l’affaiblissement d’un adversaire reste la motivation la plus susceptible de générer un effet de trappe.
En pratique, il est difficile de déterminer avec certitude la présence de l’effet de trappe dans un cas spécifique. Lorsque l’on observe un changement institutionnel important, comme une démocratisation, cela se produit souvent lors d’une période trouble, conjointement avec de nombreux autres changements. Il est donc impossible de dire, par exemple, qu’un accroissement de l’intensité d’un conflit civil est dû à l’effet de trappe. De plus, plusieurs éléments de ce mécanisme sont difficiles à observer empiriquement. Pensons entre autres au soutien étranger qui est généralement secret, ou à tout le moins discret, et difficile à quantifier. Néanmoins, plusieurs cas (dont ceux mentionnés en introduction) suggèrent, mais en aucun cas ne démontrent, que l’effet de trappe est réel et important.
Le cas du soutien soviétique à l’organisation séparatiste kurde « pkk » en Turquie est particulièrement parlant. La Turquie, voisine de la Russie, était un allié clé de l’Occident et ensuite de l’otan durant la guerre froide. Les Russes auraient donc eu des raisons de vouloir affaiblir la Turquie en soutenant et intensifiant les rébellions kurdes, ce que plusieurs sources attestent (voir entre autres McDowall 2003 ; Reynold 2016 ; Cornell 2001). Notons cependant que bien que les Kurdes aient eu un allié de taille – l’urss – ce soutien n’a jamais été suffisant pour leur assurer une victoire définitive. Cela suggère, dans l’esprit du modèle, que la Russie cherchait davantage à affaiblir la Turquie qu’à véritablement aider les rebelles kurdes à atteindre leurs objectifs. Si telle était leur stratégie, il semble qu’elle ait été efficace : on estime que les rébellions kurdes depuis les années 1980 ont causé 35 000 morts (upi 2013) et réduit le pib de l’Anatolie de l’Est et du Sud-Est de 6,6 % (Bilgel et Karahasan 2017).
La Turquie représente un cas intéressant de développement institutionnel car son histoire montre une constante fluctuation de ses institutions depuis la fin de l’Empire ottoman en 1922 et la mise en place des principes du kémalisme, tourné vers les valeurs occidentales de démocratie et de laïcité, suivie de l’institution du multipartisme en 1945 avec l’adhésion formelle à l’otan en 1952. Mais malgré une apparente amélioration de ses institutions démocratiques et légales, la Turquie subit trois coups d’État militaires en 1960, 1971 et 1980. En 1983, la Turquie revient à un régime civil et instaure une nouvelle constitution démocratique, et ce, de façon totalement pacifique.
Paradoxalement, les rébellions kurdes les plus sérieuses du pays se sont souvent produites lors de périodes de progrès institutionnel ayant le potentiel de favoriser leur inclusion économique et politique. Cela laisse penser que l’effet de trappe aurait pu être à l’oeuvre. Ainsi, la rébellion kurde la plus importante de l’histoire turque a lieu en 1925, juste après la fondation de la République et la fin de l’autoritarisme ottoman. De même, la deuxième plus importante rébellion kurde a eu lieu en 1984, juste après le retour au régime civil (McDowall 2003). La relation négative entre l’intensité des rébellions et la qualité des institutions paraît contraire à la logique, mais elle est suggérée par le modèle. Or, pour faire le lien entre ce résultat du modèle et l’histoire des rébellions kurdes, il nous faut deux éléments. Premièrement, selon le modèle, une amélioration des institutions ne devrait pas favoriser l’émergence d’une rébellion, mais pourrait en aggraver une déjà existante, ce qui semble être le cas des révoltes de 1925 et 1984. En effet, les hostilités entre le gouvernement et les Kurdes ont, dans les faits, commencé en 1920, juste avant la formation de la république, et en 1978, avant le retour pacifique au régime civil (McDowall 2003). Deuxièmement, le modèle indique que l’intensification de la rébellion devrait être causée par un plus grand soutien étranger aux rebelles, ce qui est très bien reflété par le rapprochement entre les Soviétiques et les Kurdes consécutivement à la fin du régime militaire en 1983 et suggéré par les liens forts qu’ils entretiennent dans les années 1920[16] (Reynold 2016).
Conclusion
Le nouveau cadre théorique développé dans cet article permet d’analyser le financement de groupes rebelles comme stratégie d’affaiblissement d’un pays concurrent sur le plan militaire, économique ou politique. La formalisation de ce mécanisme permet d’arriver à de nouveaux résultats théoriques. Le modèle aide à mieux comprendre comment le financement étranger affecte la situation politique d’un pays en y favorisant la guerre civile. Il permet aussi d’expliquer pourquoi l’amélioration de la qualité des institutions démocratiques et légales d’un pays, surtout lorsque cela affecte l’inclusion des minorités, peut intensifier une telle guerre par le biais d’un soutien externe accru aux rebelles.
Ce résultat adresse un message important à la communauté internationale. En effet, celle-ci joue souvent un rôle majeur dans la résolution des guerres civiles. Une option souvent privilégiée pour mettre fin à ce type de conflits est d’aider les pays à développer de meilleures institutions, afin de permettre le règlement des différends nationaux dans un cadre démocratique plutôt que militaire. Par exemple, l’onu a un vaste programme de reconstruction des institutions, particulièrement au niveau local, dans les zones post-conflits (Smith 2016). Cependant la communauté internationale doit tenir compte du fait qu’une telle amélioration des institutions peut ne pas avoir l’effet escompté et plutôt mener à une intensification du conflit par la voie d’un plus grand soutien extérieur aux groupes militants. L’option institutionnelle reste l’une des meilleures façons de mettre fin aux guerres civiles dans les pays déficients à ce niveau. Il faut cependant que cette amélioration soit suffisamment importante pour décourager l’augmentation du soutien étranger aux groupes rebelles et ainsi permettre un retour durable à une situation de paix. La communauté internationale ne doit pas se laisser décourager par l’échec de sa stratégie dans certains pays en guerre, mais plutôt redoubler d’efforts pour s’assurer que les pays en proie aux guerres civiles aient des institutions suffisamment favorables aux minorités pour endiguer les conflits. Il faut surtout qu’elle prenne en compte l’importance des acteurs internationaux dans ce type de conflits, puisque ceux-ci y jouent un rôle central et que leur présence peut fondamentalement en changer la dynamique.
Tout porte à croire que les interventions indirectes des États ne diminueront pas dans les prochaines années, à en juger par la façon dont se sont déroulées les plus récentes guerres civiles. Le conflit syrien, par exemple, a vu l’implication de l’Iran par l’intermédiaire de milices chiites dans le pays, ainsi que celles de la Russie et des États-Unis par le biais de leurs soutiens aux Kurdes (Kamel 2017). Au vu de l’évolution de la diplomatie internationale et des nouvelles technologies, il est même probable que les interventions indirectes prennent encore plus d’importance dans les guerres à venir (Mumford 2013).
Ce travail théorique ouvre la voie à des travaux empiriques importants. En particulier, il existe des données de qualité sur les guerres civiles avec soutien étranger (San-Akca 2016 ; Salehyan et al. 2011) qui pourraient permettre d’étudier quantitativement l’effet de trappe présenté dans cet article.
Annexes
A – Démonstrations
J’introduis en premier un lemme qui permet de simplifier la démonstration de la proposition 1.
Lemme 1. Le gain
obtenu par l’État étranger en fonction des capacités du pays (f) est strictement concave en
fonction de s si s![]() et est constant si s
et est constant si s ![]() . De plus, les valeurs dans la partie concave
de la fonction sont toujours plus grandes que celle de la partie
constante.
. De plus, les valeurs dans la partie concave
de la fonction sont toujours plus grandes que celle de la partie
constante.
Démonstration du lemme 1. Si ![]() alors il n’y a pas de conflit puisque (s + α0)2R < T, ce qui signifie que le
transfert est plus élevé que le gain espéré de O
en cas de conflit. Par conséquent, P=R et f est
constante en fonction de s pour tout s qui respecte cette inégalité.
alors il n’y a pas de conflit puisque (s + α0)2R < T, ce qui signifie que le
transfert est plus élevé que le gain espéré de O
en cas de conflit. Par conséquent, P=R et f est
constante en fonction de s pour tout s qui respecte cette inégalité.
Si ![]() , alors il y a un conflit et par les caractéristiques du tournoi de Tullock,
P est strictement convexe en fonction de
s. En effet,
, alors il y a un conflit et par les caractéristiques du tournoi de Tullock,
P est strictement convexe en fonction de
s. En effet, ![]() . De plus, sous l’hypothèse 1,
f est décroissante et concave. La composition de
ces deux fonctions f (P) est donc une fonction strictement concave : f (P)'' =
f "(P)[P']2 +
f '(P)[P] < 0. Finalement, les valeurs
dans la partie concave de la fonction sont toujours plus grandes que celles de la partie
constante, car R − LI −
LO < R quand
LI = LO ≠ 0. ∎
. De plus, sous l’hypothèse 1,
f est décroissante et concave. La composition de
ces deux fonctions f (P) est donc une fonction strictement concave : f (P)'' =
f "(P)[P']2 +
f '(P)[P] < 0. Finalement, les valeurs
dans la partie concave de la fonction sont toujours plus grandes que celles de la partie
constante, car R − LI −
LO < R quand
LI = LO ≠ 0. ∎
Démonstration de la proposition 1.
Si g(0) > g(s), pour tout ![]() , alors par la définition d’un optimum, l’État étranger investira
, alors par la définition d’un optimum, l’État étranger investira ![]() . Il n’y aura donc jamais de guerre civile puisque T est plus grand que le gain
espéré du groupe rebelle en cas de conflit. L’investissement de l’État étranger
n’affectera donc pas les capacités du pays (voir démonstration du lemme 1). C est
croissant et l’État étranger investira donc s*=0.
. Il n’y aura donc jamais de guerre civile puisque T est plus grand que le gain
espéré du groupe rebelle en cas de conflit. L’investissement de l’État étranger
n’affectera donc pas les capacités du pays (voir démonstration du lemme 1). C est
croissant et l’État étranger investira donc s*=0.
Les points a) et b) découlent directement du fait que est continue et strictement
concave dans l’intervalle ![]() . En effet, f en fonction de
s est concave par le lemme 1 et C est
convexe (ou linéaire) par hypothèse.
. En effet, f en fonction de
s est concave par le lemme 1 et C est
convexe (ou linéaire) par hypothèse.
Remarquons qu’avec le tournoi de Tullock, la dépense des deux acteurs est
décroissante en fonction de s quand ![]()
![]() et donc la partie concave de f est
décroissante quand
et donc la partie concave de f est
décroissante quand ![]() . Si g est décroissante sur
. Si g est décroissante sur
![]() , et donc sur tout l’intervalle, ou si
, et donc sur tout l’intervalle, ou si ![]() , alors il y a une solution en coin et cette solution est
, alors il y a une solution en coin et cette solution est ![]() . Sinon, il y a une solution intérieure (ŝ) qui est nécessairement plus petite ou égale à
. Sinon, il y a une solution intérieure (ŝ) qui est nécessairement plus petite ou égale à ![]() . ∎
. ∎
Démonstration de la proposition 2
a) Si g(0) ≤ g(s), pour au moins une valeur de
s ∈ (0,1 α0), alors cette valeur est nécessairement plus grande ou
égale à ![]() et est dans la partie concave f de
en fonction de s (proposition 1). Si T <
(α0 + ŝ)2R
alors la limite inférieure de la partie concave de la fonction
et est dans la partie concave f de
en fonction de s (proposition 1). Si T <
(α0 + ŝ)2R
alors la limite inférieure de la partie concave de la fonction ![]() est plus petite que le point où la dérivée est égale à zéro (ŝ) et par la proposition
1, s* = ŝ (par simplicité, g(0) = g(s) si pour un certain s ≠ 0, on considère que E choisit ce s).
est plus petite que le point où la dérivée est égale à zéro (ŝ) et par la proposition
1, s* = ŝ (par simplicité, g(0) = g(s) si pour un certain s ≠ 0, on considère que E choisit ce s).
b) Si T > (α0 + s̅)2R, alors par la définition de s̅, l’État étranger (E) ne voudra jamais investir suffisamment pour provoquer une révolte et il va donc investir s* = 0 par la proposition 2.
c) Si T ∈[(α0 + ŝ)2R,
(α0 + s̅)2R], alors par la définition de s̅, l’État étranger (E) voudra toujours investir suffisamment pour qu’il y ait
une guerre civile (ce qui peut être 0 si α0 est assez grand). De plus, puisque dans ce cas la limite
inférieure de la partie concave de la fonction ![]() est plus grande ou égale au point où la dérivée est égale à zéro (ŝ), cela implique que le choix optimal de s est
est plus grande ou égale au point où la dérivée est égale à zéro (ŝ), cela implique que le choix optimal de s est ![]() par la proposition 1. ∎
par la proposition 1. ∎
B – Tournoi de Tullock avec fonction de production explicite
Considérons que I et O ont des fonctions de « production militaire » qui ont une forme Cobb-Douglas. Elles ont comme entrants la technologie de conflit de chacun des acteurs (AI et AO) de même que les niveaux de capitaux (KI et KO) et le nombre de soldats (LI et LO). Les niveaux de capitaux dans ce contexte correspondent entre autres aux niveaux d’armement de I et O. J’émets l’hypothèse standard en économie que les capitaux ont des rendements marginaux non croissants (γ ≤ 1). Ainsi, le tournoi de Tullock prend la forme suivante :
![]()
Posons ![]() . On obtient :
. On obtient :
![]()
Cela correspond à la forme classique d’un tournoi de Tullock. Il y aura toujours un équilibre de Nash équivalent à celui du modèle si β < 2, ce qui est le cas lorsque les rendements sont décroissants pour le nombre de soldats. Dans le modèle, je considère que β = 1, par simplicité et parce que les résultats ne dépendent pas qualitativement de ce paramètre.
Si le coût marginal de l’augmentation du capital des rebelles (KO) est constant ou croissant pour l’État
étranger (E), alors le coût (C(s)) dans le
modèle) qu’il y aurait à augmenter l’avantage relatif du groupe rebelle (α) est croissant et convexe. Pour voir cela, remarquons en
premier qu’en inversant ![]() , on obtient
, on obtient ![]() où
où ![]() .
.
De même, ![]() et
et ![]() . Ainsi, si on note le coût comme étant C on obtient
. Ainsi, si on note le coût comme étant C on obtient ![]() puisque
puisque ![]() et
et ![]() . Ainsi, on obtient :
. Ainsi, on obtient :

La dernière ligne vient du fait que ![]() (coût marginal constant ou croissant),
(coût marginal constant ou croissant), ![]() ,
, ![]() et
et ![]()
C – Motivations alternatives pour l’État étranger
Dans le modèle principal, je considère que l’utilité de l’État étranger dépend uniquement de la perte générée par les investissements dans le conflit du gouvernement et du groupe rebelle (R − LI − LO). Dans cette annexe, je considère l’impact sur le modèle de considérer d’autres hypothèses sur la motivation de l’État étranger.
L’État étranger se soucie uniquement de la perte du côté gouvernemental : Dans certaines situations, il peut être plus logique de prendre pour hypothèse que l’État étranger ne se soucie que de la perte du côté gouvernemental (L*I). Or, L*I = L*O et le gain de l’État étranger en fonction de L*I est simplement la moitié de celui en fonction de L*I + L*O, ce qui ne change pas l’essence du modèle ou des résultats.
Destruction : de même, il serait naturel de considérer qu’un État étranger qui veut affaiblir un adversaire en finançant un groupe rebelle ne se soucie pas uniquement des investissements gaspillés dans le conflit, mais aussi de la destruction causée par ce conflit. Le modèle de destruction endogène de Chang et Luo (2017) est basé sur l’hypothèse intuitive que la destruction (D) est croissante en fonction de LI et LO. Or, si j’ajoute cette hypothèse à mon modèle, cela ne devrait pas changer qualitativement le modèle puisque D est simplement croissant en fonction de LI + LO. Mais l’ajout de D pourrait en théorie rendre LI + LO + D non concave, mais seulement quasi concave. Cela pourrait ajouter une difficulté technique supplémentaire au problème sans pour autant changer qualitativement les résultats.
Motivation à mettre le groupe rebelle au pouvoir :
dans plusieurs cas, l’État étranger peut avoir un véritable avantage à placer
au pouvoir un groupe d’opposition. Ainsi son gain ne dépend pas des ressources perdues
dans le conflit, mais de la probabilité de victoire du groupe rebelle. Celle-ci est de
zéro s’il n’y a pas de conflit et de π = α =
α0 +s sinon (Hirshleifer et Osborne 2001). Là où L*I + L*O en fonction s
est concave et croissant lorsque ![]() et décroissant lorsque
et décroissant lorsque ![]() , π est linéairement croissante en fonction de s.π atteint son maximum lorsque s = 1
- α0 et que les rebelles sont assurés de gagner.
Pour ce modèle alternatif, il est plus naturel de définir le gain de l’État étranger comme
étant simplement πV (une fonction où E n’est pas neutre au risque pourrait aussi fonctionner),
où V est ce que l’État étranger gagne si le
groupe d’opposition remporte la victoire. De même, il faudrait poser l’hypothèse que
C(s) est
croissant et strictement convexe afin de s’assurer d’avoir une solution unique.
, π est linéairement croissante en fonction de s.π atteint son maximum lorsque s = 1
- α0 et que les rebelles sont assurés de gagner.
Pour ce modèle alternatif, il est plus naturel de définir le gain de l’État étranger comme
étant simplement πV (une fonction où E n’est pas neutre au risque pourrait aussi fonctionner),
où V est ce que l’État étranger gagne si le
groupe d’opposition remporte la victoire. De même, il faudrait poser l’hypothèse que
C(s) est
croissant et strictement convexe afin de s’assurer d’avoir une solution unique.
Sans entrer trop dans les détails, on peut voir assez facilement que l’effet de trappe peut aussi être présent lorsque l’État étranger a cette autre motivation. Supposons que s* <1, un cas qui n’est pas particulièrement intéressant et ne semble de toute façon pas très réaliste. De même, supposons que lorsque T = 0, s* > 0. Autrement, nous serions dans une situation ou l’État étranger ne veut jamais soutenir les rebelles, ce qui n’a aucun intérêt ici. Par conséquent, nous devons avoir une solution intérieure lorsque T = 0 avec s* = ŝ et (π(ŝ)V = C(ŝ)). À partir de cela, on peut refaire le même raisonnement que dans le modèle de base : si on augmente T, dans un premier temps cela ne change pas s*. Ensuite, lorsque T augmente encore davantage, E est forcé d’augmenter s afin que les rebelles veuillent toujours se rebeller (s* > ŝ). Finalement, lorsque T devient très grand, il devient trop coûteux pour l’État étranger de générer une rébellion et il préfère donc s’abstenir (s* = 0). On observe ainsi qu’il y a un effet de trappe avec ce modèle alternatif. Le résultat principal reste donc qualitativement le même, et ce malgré une hypothèse très différente sur les motivations de l’État étranger. Néanmoins, le modèle de base reste une meilleure explication pour l’effet de trappe. En effet, on peut imaginer que le ŝ (l’investissement lorsque T est faible) est beaucoup plus élevé dans ce modèle alternatif, puisque l’État étranger veut donner une chance de réussite considérable au groupe rebelle et non pas seulement générer des pertes. La valeur minimale de T nécessaire pour observer un effet de trappe doit donc être significativement plus grande. On peut donc s’attendre à ce que l’intervalle de valeurs de T pour lequel on observe un effet de trappe soit plus rarement atteint en pratique.
Intérêt pour le bien-être de la minorité : pour finir, je présente une hypothèse sur les motivations de l’État étranger pour laquelle le modèle ne prédit pas d’effet de trappe. Dans certaines situations, l’État étranger peut avoir un souci réel pour le bien-être de la minorité qu’il soutient. Par exemple, il peut partager avec le groupe d’opposition des liens ethniques ou religieux forts. Dans ce cas, l’utilité de l’État étranger dépend directement de celle du groupe rebelle, que celui-ci entre en conflit ou reçoive un transfert. Ainsi l’État étranger n’a-t-il pas avantage à inciter le groupe rebelle à choisir le conflit au lieu de la redistribution, comme dans les autres modèles. Il n’y a donc pas de contrainte d’incitation et, par conséquent, pas d’effet de trappe.
Appendices
Remerciements
L'auteur tient à remercier Arthur Silve (Université Laval) pour son soutien et ses conseils lors de la rédaction de cet article.
Note biographique
L’auteur est étudiant au doctorat en économie politique à Stanford Graduate School of Business (États-Unis).
Notes
-
[1]
« Keep the pot boiling », comme le disait l’ancien président pakistanais Zia-ul-Haq en parlant du financement de groupes rebelles (Mumford 2013).
-
[2]
Voir Blattman et Miguel (2010) ainsi que Couttenier et Soubeyran (2015) pour un passage en revue des travaux sur l’économie des conflits civils.
-
[3]
Sunde et Cervellati (2013) ont cependant récemment trouvé des résultats qui vont à l’encontre de cette hypothèse.
-
[4]
Voir entre autres Gates (2002) et de Mesquita (1985) pour des modèles qui assouplissent certaines de ces hypothèses.
-
[5]
Bien entendu, je suppose que T est en général trop faible par rapport à la taille du groupe d’opposition. Par exemple, une situation où T = R serait absurde dans ce modèle puisque le groupe au pouvoir serait forcé de donner l’entièreté des ressources au groupe d’opposition. Si |I| et |O| sont la taille respective des deux groupes, alors je fais l’hypothèse que
 . Ainsi, si cette inégalité est respectée, un plus grand T signifie que le groupe d’opposition reçoit une part plus
juste (plus proportionnelle) des ressources. Avec de meilleures institutions démocratiques
et légales, cela devrait être le cas.
. Ainsi, si cette inégalité est respectée, un plus grand T signifie que le groupe d’opposition reçoit une part plus
juste (plus proportionnelle) des ressources. Avec de meilleures institutions démocratiques
et légales, cela devrait être le cas. -
[6]
Notons néanmoins que les institutions démocratiques peuvent parfois ne pas avantager les minorités. Entre autres, certaines formes de démocraties peuvent mener à une tyrannie de la majorité. Or, plusieurs indicateurs du niveau de démocratie prennent en compte la représentation des minorités, dont celui de l’Economist Intelligence Unit (2017) et de Marshall et al. (2018).
-
[7]
Voir l’annexe 3 pour une analyse du modèle avec d’autres hypothèses sur les motivations de l’État étranger.
-
[8]
Le résultat principal du modèle requiert seulement que f soit décroissante en fonction de P. Cette hypothèse serait minimaliste, ce qui montre la portée générale de ce résultat. Cependant, j’émets aussi l’hypothèse que f est deux fois dérivable (donc continue) et concave en fonction de P afin de faciliter la résolution et l’exposition du modèle.
-
[9]
Si on avait
 , nous pourrions nous retrouver dans une situation où l’État étranger
voudrait soutenir le gouvernement au lieu du groupe rebelle afin de maximiser les pertes
totales engendrées par le conflit. En effet, dans le modèle, plus les deux parties en
présence sont égales, plus les pertes sont grandes. Or, les études de cas n’indiquent pas
que les États étrangers financent d’autres gouvernements pour favoriser la discorde. De
plus, sur le plan théorique, le problème est parfaitement symétrique entre avoir
, nous pourrions nous retrouver dans une situation où l’État étranger
voudrait soutenir le gouvernement au lieu du groupe rebelle afin de maximiser les pertes
totales engendrées par le conflit. En effet, dans le modèle, plus les deux parties en
présence sont égales, plus les pertes sont grandes. Or, les études de cas n’indiquent pas
que les États étrangers financent d’autres gouvernements pour favoriser la discorde. De
plus, sur le plan théorique, le problème est parfaitement symétrique entre avoir
 et s ≥ 0, et avoir
et s ≥ 0, et avoir  et s ≤ 0.
et s ≤ 0. -
[10]
De façon générale, la dynamique du modèle étudie une série de décisions qui sont prises par les trois acteurs lorsqu’une occasion relativement rare de rébellion se présente. A priori, une analyse de long terme avec un jeu répété plus complexe ne changerait pas la dynamique de court terme qui m’intéresse ici, c’est-à-dire l’effet de trappe. Le lecteur intéressé peut tout de même consulter Maoz et San-Akca (2012) pour une analyse dynamique du soutien de groupes rebelles entre pays qui prend en compte les possibilités de représailles si l’État étranger a lui aussi un groupe minoritaire prompt à se rebeller. Il peut aussi consulter Mailath et Samuelson (2006) pour une revue des jeux répétés non coopératifs pouvant s’appliquer à ce contexte.
-
[11]
A priori, une modélisation avec une négociation à la Nash générerait un effet de trappe équivalent. Le modèle serait cependant plus compliqué et moins intuitif.
-
[12]
Par simplicité, je suppose qu’il y a une rébellion si (α0 + s)2R = T.
-
[13]
Il ne s’agit pas d’une représentation générale, mais plutôt d’une forme standard que peut prendre ce problème d’optimisation. Par exemple, f(P(s))
 avec pourrait être inférieur à zéro. Néanmoins, le point de maximum de la
partie concave de f en fonction de s est toujours à
avec pourrait être inférieur à zéro. Néanmoins, le point de maximum de la
partie concave de f en fonction de s est toujours à  si ce point est défini dans la partie concave (voir démonstration).
si ce point est défini dans la partie concave (voir démonstration). -
[14]
Formellement, cette variable serait plus précisément définie comme s̅(α0, R) puisqu’elle dépend de deux paramètres du modèle.
-
[15]
Remarquons que cette analyse n’est pas dépendante qualitativement de la concavité ou de la continuité de f. En effet, sans ces hypothèses, nous aurions encore un plancher pour s, suivi d’une augmentation avant que s retombe à 0 quand T >(α0 + s̅)2R. L’augmentation pourrait se faire de façon discontinue (par sauts), mais en aucun cas il n’y aurait de diminution, excepté quand s retombe à zéro définitivement. Comme mentionné précédemment, ces hypothèses permettent néanmoins de grandement simplifier le problème.
-
[16]
Néanmoins, l’importance du soutien russe dans la révolte de 1925 n’est pas claire dans les sources historiques.
Références
- Akcinaroglu Seden et Elizabeth Radziszewski, 2005, « Expectations, Rivalries, and Civil War Duration », International Interactions, vol. 31, no 4 : 349-374.
- Azam Jean-Paul, 2006, « The paradox of power reconsidered : A theory of political regimes in Africa », Journal of African Economies, vol. 15, no 1 : 26-58.
- Bagchi Aniruddha, João Ricardo Faria et Timothy Mathews, 2019, « A model of a multilateral proxy war with spillovers », Public Choice, vol. 179, nos 3-4 : 229-248.
- Bapat Navin, 2012, « Understanding state sponsorship of militant groups », British Journal of Political Science, vol. 42, no 1 : 1-29.
- Berman Eli et David A. Lake, 2019, Proxy Wars : Suppressing Violence through Local Agents, Ithaca, Cornell University Press.
- Bernauer Eva, 2016, Identities in Civil Conflict, Wiesbaden, Springer.
- Besley Timothy et Torsten Persson, 2011, « The logic of political violence », The Quarterly Journal of Economics, vol. 126, no 3 : 1411-1445.
- Bilgel Fırat et Burhan Can Karahasan, 2017, « The economic costs of separatist terrorism in Turkey », Journal of Conflict Resolution, vol. 61, no 2 : 457-479.
- Binmore Ken, Ariel Rubinstein et Asher Wolinsky, 1986, « The Nash bargaining solution in economic modelling », The RAND Journal of Economics, vol. 17, no 2 : 176-188.
- Blattman Christopher et Edward Miguel, 2010, « Civil war », Journal of Economic Literature, vol. 48, no 1 : 3-57.
- Cederman Lars-Erik, Kristian Skrede Gleditsch, Idean Salehyan et Julian Wucherpfennig, 2013, « Transborder Ethnic Kin and Civil War », International Organization, vol. 67, no 2 : 389-410.
- Cederman, Lars-Erik, Simon Hug et Lutz F. Krebs, 2010, « Democratization and civil war : Empirical evidence », Journal of Peace Research, vol. 47, no 4 : 377-394.
- Chang Yang-Ming et Zijun Luo, 2017, « Endogenous destruction in conflict: Theory and extensions », Economic Inquiry, vol. 55, no 1 : 479-500.
- Cornell Svante E., 2001, « The Kurdish question in Turkish politics », Orbis, vol. 45, no 1 : 31-46.
- Couttenier Mathieu et Raphael Soubeyran, 2015, « A survey of the causes of civil conflicts : natural factors and economic conditions », Revue d’économie politique, vol. 125, no 6 : 787-810.
- Cunningham David E., 2010, « Blocking resolution: How external states can prolong civil wars », Journal of Peace Research, vol. 47, no 2 : 115-127.
- De Mesquita Bruce Bueno, 1985, « The war trap revisited: A revised expected utility model », American Political Science Review, vol. 79, no 1 : 156-177.
- Fearon James D, 2004, « Why do some civil wars last so much longer than others? », Journal of Peace Research, vol. 41, no 3 : 275-301.
- Frankel Glenn, 1984, « Zimbabwe spells out its case on S. African support of rebels », The Washington Post, 23 juin, consulté sur Internet (https://www.washingtonpost.com/archive/politics/1984/06/23/zimbabwe-spells-out-its-case-on-s-african-support-of-rebels/4d3f6bf9-8242-4780-a20f-31b6b5cda4b6/) le 11 avril 2018.
- Gates Scott, 2002, « Recruitment and allegiance: The microfoundations of rebellion », Journal of Conflict resolution, vol. 46, no 1 : 111-130.
- Gause F. Gregory, 2014, « Beyond sectarianism: The new Middle East cold war », Brookings Doha Center Analysis Paper, vol. 11 : 1-27.
- Gleditsch Kristian Skrede, 2009, All International Politics Is Local: The Diffusion of Conflict, Integration, and Democratization, Ann Arbor, University of Michigan Press.
- Gleditsch Kristian Skrede, 2017, « Civil War from a Transnational Perspective », Oxford Research Encyclopedia of Politics (doi : 10.1093/acrefore/9780190228637. 013.312).
- Grossman Herschel I. et Minseong Kim, 1995, « Swords or plowshares? A theory of the security of claims to property », Journal of Political Economy, vol. 103, no 6 : 1275-1288.
- Hegre Håvard, 2014, « Democracy and armed conflict », Journal of Peace Research, vol. 51, no 2 : 159-172.
- Hegre Haavard, Tanja Ellingsen, Scott Gates et Nils Peter Gleditsch, 2001, « Toward a Democratic civil peace? Democracy, political change, and civil war, 1816-1992 », The American Political Science Review, vol. 95, no 1 : 33-48.
- Hirshleifer Jack et Evan Osborne, 2001, « Truth, effort, and the legal battle », Public Choice, vol. 108, nos 1-2 : 169-195.
- Huntington Samuel P., 1993, The Third Wave: Democratization in the Late Twentieth Century, vol. 4, Norman, University of Oklahoma Press.
- Jenne Erin, 2004, « A Bargaining Theory of Minority Demands : Explaining the Dog that Did not Bite in 1990s Yugoslavia », International Studies Quarterly, vol. 48, no 4 : 729-754.
- Kamel Lorenzo, 2017, The Frailty of Authority: Borders, Non-State Actors and Power Vacuums in a Changing Middle East, Rome, Edizioni Nuova Cultura.
- Karlén Niklas, 2019, « Turning off the Taps : The Termination of State Sponsorship », Terrorism and Political Violence, vol. 31, no 4 : 733-758.
- Konyukhovskiy Pavel V. et Theocharis Grigoriadis, 2019, « Proxy Wars et the Israeli-Palestinian Conflict », Defence and Peace Economics, vol. 31, no 8 : 904-926.
- Lee Melissa M., 2018, « The international politics of incomplete sovereignty : How hostile neighbors weaken the state », International Organization, vol. 72, no 2 : 283-315.
- Mailath George J. et Larry Samuelson, 2006, Repeated games and reputations: Long-run relationships, New York, Oxford University Press.
- Maoz Zeev et Belgin San-Akca, 2012, « Rivalry and state support of non-state armed groups (NAGs), 1946-2001 », International Studies Quarterly, vol. 56, no 4 : 720-734.
- Marshall Monty G., Keith Jaggers et Ted Robert Gurr, 2018, « Polity IV project: Political regime characteristics and transitions, 1800-2017 », Center for Systemic Peace, consulté sur Internet (https://www.systemicpeace.org/inscr/p4manualv2018.pdf) le 11 avril 2018.
- Martinez Luis R., 2017, « Transnational insurgents: Evidence from Colombia’s farc at the border with Chavez’s Venezuela », Journal of Development Economics, vol. 126 : 138-153.
- Mcdowall David, 2003, Modern History of the Kurds, Londres, ib Tauris.
- Michalopoulos Stelios et Elias Papaioannou, 2016, « The long-run effects of the scramble for Africa », American Economic Review, vol. 106, no 7 : 1802-1848.
- Mumford Andrew, 2013, « Proxy warfare and the future of conflict », The rusi Journal, vol. 158, no 2 : 40-46.
- Nedrebo Oystein, 2009, Transnational dimensions of civil conflict severity, mémoire de maîtrise, Université de Stellenbosch (Afrique du Sud), consulté sur Internet (http://scholar.sun.ac.za/handle/10019.1/2123) le 11 avril 2018.
- Padró I. Miquel Gerard et Pierre Yared, 2012, « The political economy of indirect control », The Quarterly Journal of Economics, vol. 127, no 2 : 947-1015.
- Paul Thazha V., 2005, The India-Pakistan conflict: an enduring rivalry, Cambridge, Cambridge University Press.
- Pietri Antoine, 2017, « Les modèles de “rivalité coercitive” dans l’analyse économique des conflits », Revue d’économie politique, vol. 127, no 3 : 307-352.
- Reynold Michael A., 2016, « Vladimir Putin, Godfather of Kurdistan? », The National Interest, 1er mars, consulté sur Internet (http://nationalinterest.org/feature/vladimir-putin-godfather-kurdistan-15358) le 12 mars 2018.
- Roberts Mark J., 2008, Pakistan’s Inter-Services Intelligence Directorate: A State within a State? Washington, National Defense University et Institute for National Strategic Studies, consulté sur Internet (https://apps.dtic.mil/sti/pdfs/ADA517856.pdf) le 10 mars 2018.
- Salehyan Idean, 2010, « The delegation of war to rebel organizations », Journal of Conflict Resolution, vol. 54, no 3 : 493-515.
- Salehyan, Idean, Kristian Skrede Gleditsch et David E. Cunningham, 2011, « Explaining external support for insurgent groups », International Organization, vol. 65, no 4 : 709-744.
- Salehyan Idean, David Siroky et Reed M. Wood, 2014, « External Rebel Sponsorship and Civilian Abuse: A Principal-Agent Analysis of Wartime Atrocities », International Organization, vol. 68, no 3 : 633-661.
- Sambanis, Nicholas, Stergios Skaperdas et William C Wohlforth, 2018, External Intervention, Identity, and Civil War, document de travail no 3019206, consulté sur Internet (https://papers.ssrn.com/sol3/papers.cfm?abstractid=3019206) le 11 janvier 2018.
- San-Akca Belgin, 2016, States in Disguise : Causes of State Support for Rebel Groups, Oxford, Oxford University Press.
- Sawyer Katherine, Kathleen Gallagher Cunningham et William Reed, 2017, « The Role of External Support in Civil War Termination », Journal of Conflict Resolution, vol. 61, no 6 : 1174-1202.
- Schultz Kenneth A., 2010, « The Enforcement Problem in Coercive Bargaining: Interstate Conflict over Rebel Support in Civil Wars », International Organization, vol. 64, no 2 : 281-312.
- Skaperdas Stergios, 1992, « Cooperation, Conflict, and Power in the Absence of Property Rights », The American Economic Review, vol. 82, no 4 : 720-739.
- Skaperdas Stergios, 1996, « Contest success functions », Economic Theory, vol. 7, no 2 : 283-290.
- Smith Leanne, 2016, « Institution-building as a Bridge Between Peacekeeping and Peacebuilding: Connecting the Security and Peace Nexus », Nations Unies, International Forum for the Challenges of Peace Operations, Policy Brief no 1, consulté sur Internet (https://www.un.org/pga/70/wp-content/uploads/sites/10/2016/01/PolicyBrief2016_1_Institution_building_Leanne_Smith.pdf) le 10 mars 2018.
- Sunde Uwe et Matteo Cervellati, 2013, « Democratizing for peace? The effect of democratization on civil conflicts », Oxford Economic Papers, vol. 66, no 3 : 774-797.
- Tamm Henning, 2016, « The Origins of Transnational Alliances: Rulers, Rebels, and Political Survival in the Congo Wars », International Security, vol. 41, no 1 : 147-181.
- The Economist, 2016, « Rwanda: A hilly dilemma », 12 mars, consulté sur Internet (https://www.economist.com/middle-east-and-africa/2016/03/10/a-hilly-dilemma) le 23 juillet 2021.
- Upi, 2013, « More than 35,000 dead in 30-year PKK fight », 29 janviers, consulté sur Internet (https://www.upi.com/TopNews/World-News/2013/01/29/More-than-35000-dead-in-30-year-PKK-fight/71511359473790/) le 19 avril 2020.
- Van Houten, Pieter, 1998, « The role of a minority’s reference state in ethnic relations », Archives européennes de sociologie, vol. 39, no 1 : 110-146.
- Waltz Kenneth N., 2010, Theory of international politics, Long Grove (Il.), Waveland Press.
List of figures
Figure 1
Problème d’optimisation de l’État étranger (E)
Figure 2
Soutien au groupe rebelle en fonction des institutions du pays