La microsimulation dans les projections de population Microsimulation in population projection

Résumé

Dans cet article, nous présentons un modèle de microsimulation qui permet de générer des histoires de vie individuelles cohérentes avec les projections de cohortes obtenues par le modèle multi-états à composantes de cohorte. Le modèle de microsimulation peut prendre en compte des différences individuelles que le modèle à composantes de cohorte ne peut traiter. Ces différences sont dues à une association de facteurs systématiques et de facteurs aléatoires. Nous nous intéressons principalement aux facteurs aléatoires. Le modèle de microsimulation utilise un modèle de survie de cohorte multi-états à temps continu et des tirages aléatoires à partir de distributions de temps d’attente exponentielles par morceaux. Si on prend comme paramètres des distributions les intensités de transition du modèle de survie de cohorte, les histoires de vie individuelles sont cohérentes avec les projections de cohorte. Les histoires de vie apportent un éclairage sur la dynamique démographique que la méthode des composantes ne peut proposer.

Abstract

A dynamic microsimulation model is presented to generate individual life histories that are consistent with cohort projections produced by the (multistate) cohort-component model. The microsimulation model can incorporate individual differences the cohort-component model cannot handle. The differences are outcomes of systematic factors and random factors. The paper focuses on random factors. The microsimulation model uses a continuous-time multistate cohort-survival model and random draws from piecewise exponential waiting time distributions. If the parameters of the distributions are the transition intensities of the cohort-survival model, then the individual life histories are consistent with cohort projections. The life histories provide insights in population dynamics that cannot be obtained from the cohort-component model.

Introduction

Les populations sont des systèmes d’individus. Les individus évoluent et interagissent. De ce fait, les populations évoluent également. Les modèles traditionnels de projection démographique décrivent les changements en termes de caractéristiques démographiques (p. ex. la composition par âge et par sexe) et les taux de fécondité, de mortalité et de migration (qui varient selon l’âge et le sexe). L’âge auquel les individus ont des enfants, migrent et décèdent détermine ces taux. Les parcours de vie individuels sont à la base des variations démographiques. La microsimulation dynamique est une technique qui associe les changements au niveau de la population aux parcours de vie individuels. Cet article présente un modèle de microsimulation qui génère des histoires de vie individuelles cohérentes avec les projections de cohorte obtenues par la méthode traditionnelle des composantes. Le modèle de microsimulation peut intégrer des différences individuelles qui ne sont pas prises en compte par le modèle à composantes de cohorte. Il fournit également des informations sur la répartition des intervalles entre les naissances et les durées de résidence, ce que le modèle à composantes ne peut proposer.

Le parcours de vie d’un individu change en fonction de ses expériences personnelles, de ses attentes, de ses préférences et de ses aspirations, ainsi que des événements et contextes qu’il connaît au cours de sa vie. C’est pendant les années de formation que l’impact du contexte est le plus significatif, d’où l’importance du concept de cohorte dans l’étude des changements démographiques et sociaux (Ryder, 1965). C’est également pour cette raison que, dans les modèles de projection démographique, les populations sont stratifiées par cohorte. Les modèles de projection les plus utilisés sont les modèles à composantes de cohorte qui distinguent les cohortes de naissances et les composantes des changements démographiques en termes de fécondité, de mortalité et de migration. Dans les projections démographiques fonctionnelles, la migration est remplacée par les transitions entre des états fonctionnels. Dans les projections de population relatives à l’éducation, c’est l’entrée et la sortie du système éducatif ainsi que les mouvements entre les différentes catégories éducatives (p. ex. le type d’école et le niveau) qui sont pris en compte. Dans les projections de la population active, ce sont l’entrée et la sortie du marché du travail ainsi que les mouvements entre les différentes catégories du marché du travail (p. ex. personnes en emploi/sans emploi, catégories professionnelles). Dans les projections de l’état de santé, c’est le mouvement entre les catégories d’état de santé. Dans les modèles de projection traditionnels, on étudie la fécondité, la mortalité et les passages d’un état à l’autre au niveau d’une population.

La justification des différences individuelles constitue une étape logique de la projection démographique. Mais ces différences ont-elles de l’importance ? Elles en ont, en effet. Prenons par exemple les projections de la force de travail. Les femmes d’un âge donné qui travaillent ont une fécondité plus faible que les femmes du même âge qui ne travaillent pas. Du fait de l’évolution de la fécondité, mais également de la sélection, cette différence varie toutefois dans le temps. Lorsque peu de femmes travaillent, celles qui ont un emploi sont susceptibles de se consacrer davantage à leur carrière qu’à leur famille. Elles ont souvent beaucoup moins d’enfants que les femmes qui ne travaillent pas. Lorsque les femmes sont plus nombreuses à entrer sur le marché du travail, la différence tend à s’atténuer parce qu’il y a moins de sélection et qu’il est plus facile d’entrer sur le marché du travail et d’y rester. En effet, l’intérêt public pour un équilibre entre vie privée et vie professionnelle se traduit par de meilleures structures d’accueil pour les enfants, un plus grand nombre d’emplois à temps partiel, et un renforcement de l’égalité entre les sexes, comme le montre par exemple le partage des tâches ménagères. Dans les projections traditionnelles, la diminution du différentiel de fécondité s’impose de manière exogène. Si les individus peuvent se différencier, le changement est alors endogène et peut être lié aux préférences individuelles, aux contextes institutionnels ou à d’autres facteurs non démographiques. Les modèles de projection qui acceptent cette hétérogénéité incluent une possibilité de sélection et sont plus adaptés aux théories comportementales et plus à même de rendre compte des changements temporels, souci constant de la modélisation des projections de population (Chi, 2009 ; Keyfitz, 1982 ; Sanderson, 1998 ; Willekens, 1984).

Pour rendre compte des différences entre les individus, ceux-ci sont caractérisés par des attributs soit démographiques (qui intéressent directement la projection), soit non démographiques (et donc considérés comme d’importants covariants). Le nombre et les types d’attributs pris en compte varient suivant l’objectif de la projection et la prise ou compte ou non de l’impact des facteurs institutionnels. Une des stratégies visant à intégrer les attributs personnels dans les modèles de projection consiste à stratifier la population en fonction des principaux attributs et à utiliser un modèle multi-états qui distingue les sous-populations (strates) et autorise les échanges entre les sous-populations. Une deuxième stratégie, qui peut être associée à la première, consiste à identifier une série de prédicteurs (covariants) des paramètres du modèle de projection et à spécifier un modèle de régression qui capture la relation. La microsimulation représente une troisième stratégie, qui peut être associée aux deux premières. Ces trois stratégies partagent les mêmes caractéristiques : (a) un individu est représenté par un ensemble d’attributs personnels et (b) le comportement démographique de cet individu est projeté ou prédit en se fondant sur l’expérience d’individus similaires, c’est-à-dire d’individus ayant les mêmes attributs, expérience éventuellement renforcée par des hypothèses sur leur parcours de vie future. Dans un groupe d’individus similaires, les individus partagent certains caractères, mais pas nécessairement le même parcours de vie. Les parcours de vie peuvent différer pour trois raisons : (a) les individus du groupe diffèrent en termes d’attributs omis lors de la projection, (b) des individus similaires répondent différemment aux expériences, événements et politiques et (c) des facteurs purement aléatoires. La première de ces raisons est liée à l’hétérogénéité non observée, la deuxième et la troisième aux projections probabilistes. Est-il possible de révéler les différents parcours de vie cachés dans une projection de population ? De quelle façon l’évolution des paramètres démographiques influe-t-elle sur l’évolution des parcours de vie individuels ? La microsimulation est le seul moyen d’obtenir certaines informations utiles sur les changements démographiques.

L’utilisation de la microsimulation dans les projections de population n’est pas nouvelle. Van Imhoff et Post (1998) en ont examiné plusieurs modèles. Ce qui est relativement nouveau, c’est le souci de combler l’écart entre les niveaux macro et micro. Le lien entre macro-démographie et micro-démographie a été traité (p. ex. Billari, 2006 ; Keyfitz et Caswell, 2005 ; Willekens, 2005) mais il reste beaucoup à faire pour rendre ce lien parfaitement opérationnel. Cet article a pour objectif de favoriser le rapprochement entre projections démographiques et projections biographiques. Les projections démographiques utilisent la méthode des composantes de cohortes, qui prévoit une projection des caractéristiques démographiques par cohorte de naissance. Ce modèle permet d’obtenir, pour chaque cohorte de naissance et à des moments successifs dans le temps, le nombre d’individus en fonction du sexe et d’autres attributs démographiques choisis pour la projection. À mesure de l’avancée en âge de la cohorte, les caractéristiques changent. Ryder (1965) considère cette séquence de caractéristiques comme étant la « biographie de la cohorte ». Le modèle multi-états par composantes permet d’obtenir des biographies de cohortes synthétiques. Les projections biographiques, ou projections des parcours de vie individuels, se fondent le plus souvent sur la microsimulation dynamique (pour une discussion, voir Willekens, 2009). À ce jour, la microsimulation dynamique et la méthode des composantes de cohorte n’ont pas encore été associées. C’est ce que nous tentons de faire ici.

Le modèle multi-états par composantes constitue la première étape de cette démarche. Pour rendre compte des différences individuelles, on développe la projection de la cohorte par des projections des parcours de vie individuels des membres de cette cohorte, les « biographies individuelles ». La méthode de la microsimulation dynamique a été choisie parce que les individus peuvent avoir des enfants, migrer ou décéder à n’importe quel moment ou n’importe quel âge. Le temps écoulé jusqu’à l’événement dépend de facteurs systématiques ou covariants (certains individus ont plus de probabilité de connaître un événement plus tôt ou plus tard) et du hasard. Nous nous intéresserons particulièrement à l’effet du hasard. Dans cet article, les covariants sont mentionnés de manière sporadique. Il est important qu’il y ait une cohérence entre les biographies individuelles générées par la microsimulation et les biographies des cohortes obtenues par la méthode des composantes. Dans les projections de population traditionnelles, cette cohérence est garantie parce que l’on suppose qu’une cohorte est homogène, c’est-à-dire que tous les membres de la cohorte sont identiques, et qu’on ne tient pas compte des facteurs aléatoires. Dans les modèles de microsimulation qui sont utilisés aujourd’hui, ce critère de cohérence est soit négligé soit imposé ex post à l’aide de procédures d’alignement qui imposent une correspondance entre les prévisions obtenues à partir de données agrégées et les prévisions externes (voir p. ex Zaidi et Rake, 2001). Dans cet article, nous décrivons et illustrons une méthode qui garantit la cohérence entre les biographies individuelles et les biographies de cohortes, sous certaines conditions.

Nous présentons les principaux enjeux liés au rapprochement micro-macro dans les projections de population, puis le modèle à composantes de cohorte, puis le modèle de microsimulation. Une simple illustration chiffrée sert à démontrer comment l’écart micro-macro peut être comblé et comment les projections au niveau macro et au niveau micro sont liées entre elles. Nous présentons ensuite les indicateurs qui ne peuvent être obtenus que par microsimulation. Enfin, le modèle à composantes de cohorte est associé à la microsimulation et appliqué pour projeter les histoires d’incapacité d’une cohorte synthétique d’individus âgés de 55 ans à l’aide des taux de transition entre les différents niveaux d’incapacité définis à partir de l’enquête américaine Santé et Retraite et des données sur la mortalité issues du Registre national des décès (National Death Index).

Combler l’écart micro-macro dans les projections de population

Une projection de population consiste à calculer le nombre d’individus prévus par âge et par sexe à différents intervalles de temps à partir d’un point de départ (Keyfitz, 1968 : 27). Dans les projections de population fonctionnelles, d’autres attributs sont pris en compte outre le sexe. Le modèle des composantes de cohorte utilise les taux de natalité, de mortalité et de mobilité spécifiques de la cohorte de naissance pour calculer le nombre prévu d’individus. Dans cette partie comme dans le reste du présent article, les taux de mobilité sont appelés taux de transition, conformément à la terminologie de l’analyse de survie et de l’analyse de l’historique des événements. Le nombre prévu d’individus par âge, par sexe et autre attribut à un moment futur donné peut être obtenu à partir de la population actuelle et du comportement du système de la population dans son ensemble pendant un temps donné. Dans ce cas, le comportement du système de la population est documenté en termes de taux de natalité, de mortalité et de transition entre les différents états fonctionnels. Le nombre prévu d’individus peut également être obtenu à partir de la population actuelle et du comportement démographique des acteurs individuels de cette population. Si pour chaque femme d’une population donnée ou pour une femme représentative d’un groupe de femmes similaires, nous pouvions connaître les intentions de grossesse pour les 12 prochains mois, nous serions en mesure de projeter le nombre de naissances après correction pour tenir compte des différences évidentes entre ces intentions et leur réalisation. Selon cette approche, la dynamique du système de population est déterminée par des processus internes au système au niveau des individus. La prédiction du comportement du système sur la base des actions, des attentes, des intentions et des attitudes des acteurs à un niveau inférieur à celui du système est fortement liée au mode d’explication du comportement du système adopté par Coleman (1991) et généralement appelé « individualisme méthodologique », expression forgée par Schumpeter en 1909. Selon cette approche, les changements au niveau du système qui résultent des actions et interactions individuelles ne sont ni intentionnels ni prévus par les individus (Coleman, 1991 : 5). De Bruijn (1999) a développé une base théorique du changement démographique selon la méthode de l’individualisme méthodologique. Pour les projections de population, cette méthode se justifie, parce qu’à la différence des systèmes sociaux, le système de population n’influence pas sa dynamique de manière autonome. Peu de personnes adaptent leurs désirs d’enfants en réponse à la croissance de la population et peu de personnes également adaptent leur style de vie à cause d’une augmentation des décès dans leur pays. La dynamique des populations est en grande partie déterminée par les actions des individus, par les interactions entre individus et les réponses individuelles aux facteurs et politiques institutionnels et autres variables liées au contexte. Cette perspective laisse suffisamment de place à l’influence des normes, institutions, politiques, événements historiques et autres types d’expériences collectives sur les actions et interactions individuelles. La figure 1 illustre la méthode de l’individualisme méthodologique appliquée à la projection démographique. La méthode de projection la plus répandue, c’est-à-dire la méthode des composantes, permet de prédire la taille et la structure de la population uniquement à partir de variables systémiques. La microsimulation dynamique, en revanche, décrit la dynamique au niveau micro. Cette méthode permet d’obtenir la probabilité pour un individu avec un nombre donné d’attributs aujourd’hui d’être vivant à un moment donné à l’avenir avec un ensemble donné d’attributs.

Figure 1

Le lien micro-macro en projection démographique

Nous utilisons le modèle de survie pour projeter les expériences des cohortes (biographies de cohorte) et des expériences individuelles (biographies individuelles). Nous utilisons les mêmes valeurs de paramètres. Les paramètres estimés à partir de données sont des estimations ponctuelles ou valeurs attendues que l’on utilise dans le modèle macro. Le modèle micro prend en compte les idiosyncrasies individuelles qui entraînent des différences de valeur de paramètres d’un individu à l’autre. Les valeurs possibles d’un paramètre donné sont représentées par une distribution de probabilité. En microsimulation, les valeurs des paramètres sont dérivées d’une distribution de probabilité. Les paramètres utilisés à la fois dans le modèle macro et le modèle micro sont les taux de transition (taux de naissance, taux de mortalité et taux de mobilité). Les taux sont avant tout des ratios nombre d’événements / temps d’exposition. En démographie, on les désigne comme des taux d’occurrence-exposition, dans lesquels le nombre d’occurrences est le nombre d’événements. Les taux de transition sont estimés à partir de données empiriques, qui sont des données sur la population (données d’état civil) ou microdonnées. L’estimation des taux de transition à partir de données individuelles s’appuie sur des techniques de survie et sur l’analyse de l’historique des événements (voir Aalen, Borgan et Gjessing, 2008 ; Blossfeld et Rohwer, 2002).

L’approche de la survie par cohorte

Pour illustrer la procédure, prenons un modèle simple avec les taux de transition seulement. Le modèle est désigné comme modèle de transition plutôt que modèle des composantes de cohorte. J’illustre d’abord le calcul des taux de transition. J’utilise ensuite les taux pour produire des biographies de cohortes et des biographies individuelles. Considérons une cohorte de 1 000 individus et trois états fonctionnels possibles (A, B et C). Au début de l’observation, 400 personnes sont dans l’état A, 300 en B, et 300 en C. Durant la période d’observation de deux ans, 150 personnes sortent de l’état A, 100 personnes vers B, et 50 vers C. Les dates de ces sorties seront fournies. Supposons que parmi les 150 qui sortent de A, 50 sortent 6 mois après le début de l’observation, 50 exactement un an après et 50 au bout de 18 mois. Supposons aussi que durant la période d’observation, 70 personnes entrent dans l’état A en venant de B et 50 en venant de C, et qu’elles entrent exactement un an après. Le temps passé dans l’état A par les membres de la cohorte se calcule comme suit. Parmi les 400 individus présents en A au début de l’observation, 250 restent en A pendant toute la période d’observation. Ils contribuent pour 250*24 = 6000 mois à la durée d’exposition. Les 50 personnes qui sortent de A à 6 mois contribuent 50*6 = 300 mois à la durée d’exposition. Les 50 personnes qui sortent à 12 mois contribuent 50*12 = 600 mois et les 50 personnes qui sortent à 18 mois contribuent 50*18 = 900 mois. Les personnes en A au début de l’observation contribuent 7800 mois à la durée totale d’exposition en A. Au total, 1800 mois sont perdus du fait de la sortie de A. La durée d’exposition n’est pas affectée par la destination, mais par la date de départ. Les individus qui entrent en A durant la période d’observation contribuent également à la durée d’observation. Leur contribution est la suivante : 70*12 + 50*12 = 1440 mois. La durée totale d’exposition en A durant la période d’exposition est 6000 + 1800 + 1440 = 9240 individu-mois ou 770 individu-années. Le taux de transition de A à B est de 100/770 = 0,1299 par an. Le taux de transition vers C est de 50/770 = 0,0649 par an. Le taux de sortie de A est de 150/770 = 0,1948 par an.

Pour illustrer la relation entre la projection de la cohorte et la microsimulation, prenons une cohorte de 10 000 individus, trois états (A, B, C) et des taux de transition qui ne varient pas dans le temps. Au démarrage de l’étude, soit à t = 0, on suppose que 40 % des individus sont à l’état A, 30 % à l’état B et 30 % à l’état C. Le taux de sortie de A est de 0,15, dont deux tiers pour aller en B et un tiers pour aller en C. Les taux de transition se présentent en matrice, avec des valeurs en diagonale égales au total des taux de sortie des états :

Le schéma de la matrice des taux de transition est conforme à l’usage en démographie multi-états (voir Preston, Heuveline et Guillot, 2001 : 268 ; Rogers, 1975 ; Schoen, 1988). Il est différent de ce qui est prévu par les conventions en statistique (voir p. ex. Aalen, Borgan et Gjessing, 2008 : 466), mais cette différence n’est pas d’une importance majeure pour la modélisation. On désigne par m la matrice de la transition :

Pour inclure la fécondité et la mortalité à la matrice, aux fins de la projection, nous ajoutons des taux par état à la diagonale, les taux de décès étant indiqués avec un signe positif et les taux de naissances avec un signe négatif.

La matrice de transition contient les paramètres du modèle de projection multi-états. La population à l’instant t+1 dépend de la population à l’instant t et des taux de transition pendant l’intervalle de t à t+1. En l’absence de naissances et de décès, la taille de la population est fixe et le modèle décrit alors le mouvement d’un état à l’autre. La répartition par état à l’instant t s’obtient par le modèle de projection K(t) = P(t - 1)P(t - 2) ... P(0) K(0), dans lequel k(t) est le vecteur d’état indiquant pour l’instant t le nombre de membres de la cohorte par état et P(t) la matrice des probabilités de transition durant l’intervalle de t à t+1, qui dépend des taux de transition pendant l’intervalle : P(t) = exp [-m(t)]. Si h est la durée de l’intervalle pendant lequel les taux de transition restent constants, alors le modèle de projection peut s’écrire comme l’équation récursive

1

k(t + h) = P(t) k(t) = exp [- h * m (t)] k(t)

dans laquelle P(t) est la matrice des probabilités de transition qui s’applique à un intervalle de temps de durée h. Un élément p_ij de P(t) est la probabilité qu’un membre de la cohorte en i à l’instant t soit en j à t+h. L’exponentielle de la matrice s’obtient par un développement en série de Taylor ou par décomposition spectrale de m(t). Les taux de transition sont supposés constants. Les probabilités de transition sont les suivantes :

La probabilité qu’un membre de la cohorte à l’état A à l’instant t soit à l’état B à t+1 est de 8,1 %. Au total, 87,6 % des membres en A à l’instant t sont également en A à t+1. Certains d’entre eux peuvent être sortis de l’état A puis revenus en A avant la fin de l’intervalle.

La projection en supposant des taux de transition constants est indiquée dans tableau 1.

Tableau 1

Projection de la cohorte multi-états : modèle des composantes de cohorte

La projection donne le nombre prévu d’individus par état fonctionnel.

Les taux de transition peuvent aussi être utilisés pour dériver le temps passé par les individus aux différents états. Un individu dans un état donné étant exposé au risque de sortir de cet état, le temps passé dans cet état est également le temps d’exposition ou durée d’exposition. On distingue trois types de temps de séjour prévus. Le premier est le temps de séjour prévu dans un état avant la sortie de cet état. Ce temps de séjour prévu est de 1 divisé par le taux de sortie. Il est égal à 1/0,15 = 6,67 années à l’état A, 1/0,40 = 2,5 années à l’état B et 1/0,35 = 2,86 années à l’état C. Cela signifie qu’un individu à l’état A peut s’attendre à passer encore 6,67 ans à l’état A avant d’en sortir. La procédure de sortie à taux constant étant sans mémoire, la durée de séjour prévue est indépendante de la durée effective du séjour. Le deuxième type de temps de séjour prévu est la durée de séjour prévue dans un état entre deux instants. Considérons le membre d’une cohorte à l’état A à l’instant t = 0. Le temps de séjour prévu en A entre 0 et t constitue la zone sous la courbe de survie de 0 à t. Elle s’exprime ^tL_A (0) = ʃ^t₀ S_A(τ) dτ dans lequel S_A est la fonction de survie : S_A (τ) = exp [- ʃ^τ₀μ_A+ (ξ) dξ], avec μ_A+(ξ) le taux de sortie de A à l'instant ξ. Si le taux de transition est constant, la fonction de survie est la suivante : S_A (τ) = exp [- τμ_A+]. Le temps de séjour prévu est alors : , avec m_A+ le taux de sortie de A. Pour la dérivation, voir Willekens (2007 : 48). C’est le produit du temps de séjour prévu avant la sortie de l’état et de la probabilité de sortie de l’état avant t. Pendant les 10 premières années après le début de l’observation (t = 10), un membre de la cohorte à l’état A à l’instant 0 peut s’attendre à passer 5,18 ans à l’état A avant d’en sortir. Le troisième type de temps de séjour prévu est le temps de séjour total prévu entre deux instants. Un membre de la cohorte en A au début de l’observation peut sortir de cet état et y revenir une ou plusieurs fois avant la fin de la période, disons à l’instant t. Le temps passé en A entre 0 et t dépend du taux de sortie de A mais également des taux de sortie des 0utres états et en particulier du taux de sortie d’un autre état pour entrer en A. En résumé, il dépend de l’ensemble des taux de transition. Le temps de séjour prévu à chacun des états durant la période de 0 à t, par état occupé à l’instant 0, est donné par l’expression de la matrice : ^tL(0) = m^-1 [I - exp( -tm)], dans laquelle m est la matrice des taux de transition, I la matrice identité et ^tL(0) la matrice des durées totales de séjour prévues. Un élément ^tL_AB(0) de ^tL(0) désigne le nombre total d’années qu’un membre de la cohorte à l’état A à l’instant 0 peut s’attendre à passer à l’état B avant la fin de t. Les éléments diagonaux de [I - exp( -tm)] indiquent les probabilités de sortie d’un état. Les éléments hors de la diagonale sont les probabilités inférieures de sortie de l’état d’origine pour un état de destination. La matrice m^-1 permet d’obtenir le temps de séjour total prévu dans les différents états avant l’entrée dans un état absorbant, c’est-à-dire un état dont on ne peut sortir une fois qu’on y est entré. Pour illustrer cela, faisons de C un état absorbant en donnant au taux de sortie de C la valeur zéro. Le nombre d’années prévues en A et B avant d’entrer en C s’obtient en inversant les deux lignes et les deux colonnes en coin supérieur gauche de m. Remarquons que l’élément diagonal est la somme des sorties vers l’autre état transitoire et l’état absorbant. Un membre de la cohorte en A à l’instant t peut s’attendre à passer 13,3 ans en A et 3,3 ans en B avant d’entrer en C. Un membre de la cohorte commençant à l’état B peut s’attendre à passer 10 ans en A et 5 ans en B avant d’entrer en C. Lorsque tous les états sont des états transitoires, c’est-à-dire qu’il est possible d’en sortir puis d’y entrer à nouveau, le temps de séjour total prévu pour chaque état est infini[1]. Le temps total qu’un membre moyen de la cohorte peut s’attendre à passer dans chacun des états durant une période de 10 ans, lorsque tous les états sont transitoires, est indiqué tableau 2.

Tableau 2

Temps de séjour prévu dans les trois états, par état d’origine

Un membre de la cohorte qui commence à l’état A peut s’attendre à passer 7,1 ans en A, 1,8 an en B et 1,1 an en C. Les individus qui commencent en B ou C passent davantage de temps en A que dans n’importe quel autre état. C’est là une conséquence d’un taux élevé de transition vers A et d’un taux de sortie de A relativement faible.

L’approche de la microsimulation

Les informations fournies par les taux de transition concernent la biographie de la cohorte. Considérons à présent les biographies individuelles et supposons que les différences entre les membres de la cohorte sont seulement dues au hasard. Les biographies individuelles sont établies à partir des mêmes taux de transition qui servent à obtenir les biographies de cohortes. Les biographies individuelles fournissent des informations complémentaires sur la cohorte, notamment la proportion de membres de la cohorte commençant à l’état A qui font un séjour en B et C avant de revenir à l’état A, ainsi que les temps de transition prévus. Autre exemple, la proportion d’individus sortant de A qui ne reviennent pas avant la fin de l’étude.

La génération de biographies individuelles nécessite des tirages aléatoires à partir d’une distribution de probabilité, et plus particulièrement de la distribution des temps d’attente. Supposons un individu à l’état i à l’instant 0. Les temps d’attente en i jusqu’à un déplacement potentiel vers un état de destination j, T_ij, peuvent être simulé à l’aide de la fonction de distribution inverse ou fonction quantile (Rubinstein et Kroese, 2008 : 53f ; Gampe et collab., 2009 : 3 ; Willekens, 2009). Il s’agit d’une pratique courante en simulation à événements discrets[2]. La fonction quantile est une des fonctions de probabilité qui caractérisent une variable aléatoire. Prenons μ_ij (t) pour désigner le taux instantané de transition de l’état i à l’état j à un instant t. La fonction de survie est S_ij (t) = exp [- A_ij (t)], où A_ij (t) = ʃ^t₀ μ_ij (τ) d τ est le taux de transition cumulé. Si le taux de transition est constant entre 0 et t, alors la fonction de survie est S_ij (t) = exp [- t μ_ij]. La fonction de distribution est F_ij (t) = 1 - exp [- A_ij (t)]. La fonction de distribution associe à un nombre réel (une valeur particulière t d’une variable aléatoire T) une probabilité. Le nombre réel associé à une probabilité est le quantile de la variable aléatoire (voir Evans et al., 2000 : 5). Par conséquent, t est le quantile de T. À t est associée une probabilité, disons α, et la fonction de distribution indique la probabilité que T ne soit pas supérieur à t. La fonction de distribution inverse de T, indiquée par F^-1(t) et G(α), est la valeur de t (quantile) telle que la probabilité que T ait une valeur inférieure ou égale à t est α : Pr{T≤G(α)}= α = F(G(α)) = F(t). G(α) donne la valeur t pour laquelle F(t) = α. Le quantile G(α) est le 100α quantile. La fonction de survie inverse Z(α) est le quantile qui est dépassé avec la probabilité α : Pr{T>Z(α)}=α = S(Z(α)). Les fonctions de distribution inverses sont largement utilisées en statistique, notamment pour déterminer les intervalles de confiance. Notons que Z(α) = G(1-α).

La fonction de distribution inverse est utilisée pour générer des nombres aléatoires à partir de la distribution d’une variable aléatoire. Si G(T) est la fonction de distribution inverse de T, alors U = G(T) suit une distribution uniforme sur un intervalle de 0 à 1. Dans une simulation de Monte Carlo, un tirage aléatoire à partir d’une fonction de distribution comporte deux étapes. Tout d’abord, une valeur aléatoire pour la probabilité α est extraite de la distribution uniforme U[0,1] (remarquons que G(T) suit la distribution U[0,1]). Ensuite, à l’aide de la fonction de distribution inverse G(α), la probabilité est associée à un nombre réel t, qui indique le moment de la transition. La première étape est indépendante du modèle de transition ou de la distribution du temps d’attente utilisée. Pour plus de détails, voir Willekens (2009).

Parmi les distributions du temps d’attente les plus utilisées figurent la distribution exponentielle, la distribution de Weibull et de Gompertz. Si le taux de transition est constant, la distribution du temps d’attente est exponentielle. La fonction de distribution inverse ou fonction quantile de T est . Si le taux de transition est de forme irrégulière, le taux de transition constant par morceaux constitue une approximation appropriée, qui implique un risque linéaire cumulé par morceaux.

Considérons le modèle multi-états. Si U désigne un nombre aléatoire standard uniformément distribué, c’est-à-dire U ∼ U[0,1], il est possible de créer un temps d’attente aléatoire T_ij à partir d’une distribution donnée en dérivant une valeur α de la distribution uniforme et en prenant la fonction de distribution inverse :

T_ij = A_ij-1 (T_ij) [- 1n(1 - α)] j ≠ i et j ∈ {A, B, C}

avec le risque cumulé A_ij (T_ij) = ʃ^Tij₀ μ_ij (τ) d τ, soit T_ij*m_ij si le taux est constant. Un temps d’attente aléatoire est sélectionné pour chaque destination possible. Selon la théorie des risques concurrents, le temps d’attente le plus court détermine l’état de destination, c’est-à-dire que la transition se fait de i à k à condition que la réalisation de la variable aléatoire T_ik soit inférieure à la réalisation de la variable aléatoire T_ij pour tout j ≠ k. Ce calcul du temps d'attente le plus court est répété pour chaque membre de la cohorte jusqu'à écoulement de la durée de simulation programmée ou jusqu'à ce que l'individu ait atteint un état absorbant. La distribution des temps d'attente dépend de la forme des taux de transition instantanés μ_ij(t). Lorsque le taux de transition est constant, la distribution appropriée est la distribution exponentielle.

Considérons un individu à l’état A à l’instant 0 dont le parcours de vie est déterminé par la matrice de transition m et le hasard est représenté par une distribution de probabilité. Le parcours de vie est une réalisation obtenue par une chaîne de Markov à temps continu jusqu’à un instant donné, soit 10 ans dans le cas présent. Les taux de sortie de A vers B et C sont respectivement de 0,10 et 0,05. Pour déterminer le moment de la transition et la destination, deux nombres aléatoires sont obtenus à partir d’une distribution uniforme. Le premier nombre obtenu (pour la transition AB) est 0,2 et le deuxième (pour la transition AC) 0,7. Le temps d’attente aléatoire associé à la transition AB est -ln(1-0,2)/0,10 = 2,23 ans. Le temps d’attente aléatoire associé à la transition AC -ln(1-0,7)/0,05 = 24,08 ans. Le temps d’attente le plus court détermine le moment de la transition et sa direction. La transition se produit 2,23 ans après le démarrage de l’étude. L’individu passe de l’état A vers l’état B. Les taux de sortie de B sont de 0,30 (BA) et 0,10 (BC). Deux tirages aléatoires à partir de la distribution uniforme donnent 0,4 et 0,6, les temps d’attente aléatoires associés étant -ln(1-0,4)/0,30 = 1,70 an et -ln(1-0,6)/0,10 = 9,2 ans. À 1,7 an après la transition AB, soit 3,93 ans après le démarrage de l’étude, l’individu revient à l’état A. On répète le processus jusqu’à ce que la période d’étude de 10 ans soit atteinte. La matrice des taux de transition et les tirages aléatoires réalisés à partir des distributions exponentielles des temps d’attente donnent le parcours de vie suivant : AB à 2,23 ans, BA à 3,93 ans et AC à 9,1 ans.

La simulation permet de générer les parcours de vie pour 10 000 individus, dont 4 000 commençant à l’état A, 3 000 à l’état B et 3 000 à l’état C. La matrice des taux de transition gouverne les trajectoires. Dans le présent article, nous ne prenons en compte aucun covariant. Les taux de transition par origine et destination constituent les paramètres des différentes distributions exponentielles du temps d’attente. Les parcours de vie individuels sont déterminés par des tirages aléatoires à partir des distributions exponentielles, à l’aide de la théorie des risques concurrents. Cette opération est réalisée par un logiciel de microsimulation. Nous avons utilisé ici la fonction sim.msm du package msm développé par Jackson (2010) et archivé dans le réseau CRAN (Comprehensive R Archive Network). Cette fonction implémente globalement la même méthode de simulation à événements discrets (Discrete Event Simulation) décrite au paragraphe précédent. Dans ce type de simulation, le système évolue de façon discrète, dans le temps, d’un événement à l’autre. La fonction sim.msm simule une réalisation à partir d’une chaîne de Markov à temps continu avec des taux de transition donnés jusqu’à un instant donné, soit 10 ans dans le cas présent. En d’autres termes, elle simule la trajectoire entière pour un individu isolé. En lançant cette fonction de multiples fois, on obtient la simulation des trajectoires pour toute une cohorte. Les parcours de vie simulés sont stockés dans un objet Biograph, objet en R avec une structure pouvant être utilisée comme entrée dans le package Biograph (Willekens, 2011 et à paraître).

Tableau 3

Projection de cohorte obtenue par la microsimulation

Les résultats de la microsimulation sont très proches des nombres prévus d’individus par état obtenus par le modèle à composantes de cohorte (tableau 1). La différence est due à la variation de l’échantillon, et plus précisément la variation Monte Carlo. La microsimulation peut être considérée comme l’échantillonnage d’une population virtuelle avec des paramètres démographiques (taux de transition) identiques à ceux estimés à partir de données réelles. Plus l’échantillon est important, plus les caractéristiques de l’échantillon se rapprochent des valeurs prévues.

La durée totale qu’un membre moyen de la cohorte peut s’attendre à passer dans chacun des états pendant une période de 10 ans peut facilement être dérivée des biographies individuelles (tableau 4).

Tableau 4

Temps de séjour total dans les différents états, selon l’état d’origine (échantillon de population virtuelle)

Dans l’échantillon de population virtuelle, un membre de la cohorte qui commence à l’état A peut s’attendre à passer 7,4 ans en A (valeur prévue 7,1 ans), 1,6 an en B (valeur prévue 1,8 an) et 1,0 an en C (valeur prévue 1,1 an). C’est le troisième type de temps de séjour (prévu). Le deuxième type est représenté par le temps prévu passé dans un état entre deux instants. Un membre de la cohorte à l’état A à l’instant 0 peut s’attendre à passer 5,18 ans en A avant de sortir de cet état (voir plus haut). Dans l’échantillon de population virtuelle, un individu commençant en A reste en A pendant 5,24 ans avant de passer à un autre état ou d’arriver à la fin de l’étude au bout de 10 ans. Parmi les 4 000 individus virtuels qui commencent en A, 930 restent en A pendant toute la durée de l’étude et 3 070 sortent de A pour aller en B ou en C avant la fin de l’étude. Ceux qui sortent de l’état initial A pour aller en B ou C avant la fin de l’étude font cette transition au bout de 3,8 ans en moyenne.

Les valeurs indiquées dans le tableau 4 sont différentes de celles du tableau 2. Le tableau 2 indique les valeurs attendues tandis que le tableau 4 indique la moyenne des valeurs obtenues dans l’échantillon. La taille de l’échantillon est de 10 000 individus. Des échantillons différents produisent des résultats différents qui fluctuent autour des valeurs attendues. Si la taille de l’échantillon augmente de 50 000, alors les valeurs de l’échantillon coïncident avec les valeurs attendues indiquées au tableau 2.

Résultats complémentaires

L’utilisation de la microsimulation comme outil de développement des projections de population a pour objectif d’obtenir des informations pertinentes sur les changements démographiques qui ne peuvent s’obtenir autrement. Dans les projections obtenues par les modèles à composantes de cohorte, ces informations restent cachées, tandis que la technique de microsimulation permet de les extraire. Plus précisément, elle permet d’extraire des informations sur les parcours de vie individuels totalement cohérentes avec l’expérience de la cohorte ou la dynamique démographique décrite par le modèle de projection. Les informations obtenues sont considérées comme fiables si les résultats de la microsimulation et les résultats obtenus par le modèle à composantes ou un autre modèle de projection sont suffisamment proches. Parmi les informations extraites grâce à la microsimulation, celles qui concernent les trajectoires présentent un intérêt particulier. Dans la population virtuelle, près d’un individu sur quatre qui commence en A reste en A pendant toute la période d’étude (10 ans). Ceux qui passent à l’état B ou C ont de fortes chances de revenir en A. Pas moins de 40 % de ceux qui sortent de A à un moment ou un autre y reviennent au moins une fois et sont en A à la fin de l’étude. La moitié des individus de l’échantillon virtuel de population ont une trajectoire parmi un choix de quatre trajectoires différentes, et 75 % une trajectoire parmi un choix de dix. Les trajectoires les plus fréquentes sont indiquées tableau 5.

Tableau 5

Trajectoires les plus fréquentes (population virtuelle)

ncas, nombre de trajectoires ; %, pourcentage ; cum %, pourcentage cumulé ; ns, nombre d’états par trajectoire ; cas, trajectoire ; tr, transition.

Le tableau montre le nombre de trajectoires (ncas), le pourcentage (%), le pourcentage cumulé (cum %), le nombre d’états par trajectoire (ns), la trajectoire (cas), et pour chaque transition (tr) de la trajectoire le moment de la transition et l’état de destination. Par exemple, 17,4 % de ceux qui commencent en A ont une trajectoire ABA, la première transition intervenant à 3,9 ans et la deuxième à 5,9 ans. Les moments des transitions, et par conséquent les intervalles entre les transitions, diffèrent largement d’une trajectoire à l’autre. Des résultats similaires sont obtenus pour les individus virtuels commençant en B et C. Les chiffres indiquent une variation très importante des parcours de vie. Certains parcours sont toutefois plus fréquents. Les chiffres montrent aussi que les taux de transition qui en régissent la dynamique montrent qu’une proportion très importante d’individus en B ou C se déplace en A. Dans une population multi-états, les trajectoires peuvent servir à interpréter des séries de taux de transition.

L’exploration des histoires de vie individuelles cachées à l’intérieur des projections démographiques apporte un éclairage supplémentaire sur ces dernières, ce qui est particulièrement utile pour étudier les effets des variations des paramètres démographiques. Supposons par exemple que le taux de transition de B à C augmente de 0,1 à 0,3. Ce changement implique que la probabilité pour un individu en B d’être en C un an plus tard passe de 7,5 % à 19,6 % et la probabilité qu’il reste en B baisse, passant de 69 % à 58 %. Cela signifie également que dix ans plus tard, 23 % de la population sera en C et 18 % en B, un résultat très différent de celui obtenu avec la projection précédente qui donnait 17 % en C et 23 % en B (à condition que la répartition par état à l’instant 0 soit inchangée). Le temps médian de la transition de B vers C pour un individu qui l’expérimente pour la première fois baisse de 4,3 ans à 3,7 ans (baisse moyenne de 4,5 à 4,2). Cela signifie en outre que les individus sont légèrement plus mobiles, et que la part de leur trajectoire ABC dans toutes les trajectoires possibles double, passant de 3 % à 6 % tandis que la part de la trajectoire ABA diminue, de 17 % à 11 %. La part de la trajectoire BA baisse également, de 24 % à 14 %, tandis que celle de la trajectoire BCA augmente, de 5 à 9 %. Lorsqu’un des taux de transition augmente, cela affecte les parcours de vie dans l’ensemble du système de population.

Illustration : Vieillissement et incapacité

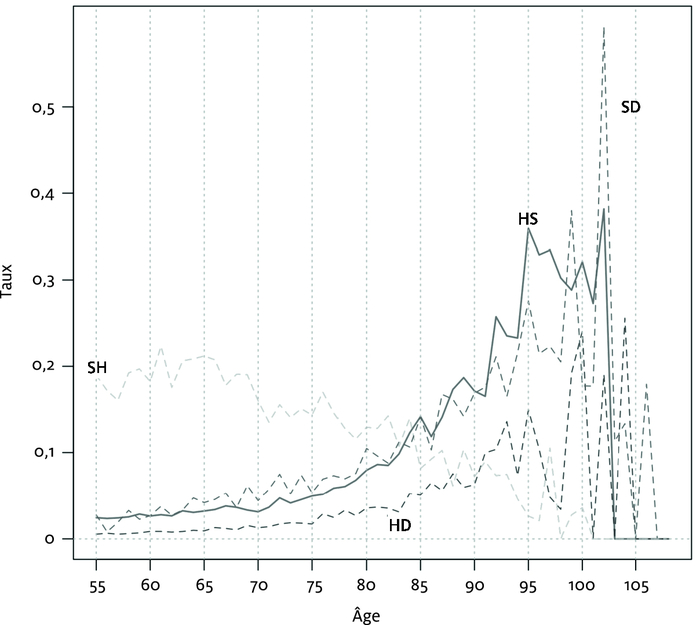
Dans cette partie, nous appliquons le modèle à composantes de cohorte pour projeter les niveaux d’incapacité d’une cohorte actuellement âgée de 55 ans, et estimer le nombre d’années prévues en état d’incapacité. Nous utilisons la microsimulation pour explorer les trajectoires d’incapacité des membres de la cohorte. Nous nous intéressons particulièrement au nombre et à la durée des périodes d’incapacité prévues. Lorsque le taux de survie des personnes âgées augmente, cela signifie-t-il pour ces personnes un plus grand nombre d’années en incapacité, ou bien une durée de vie plus longue avec un retard d’incapacité (compression de l’incapacité) ? L’accroissement de la longévité s’accompagne-t-il de périodes plus longues d’incapacité ou d’un plus grand nombre de périodes d’incapacité de courte durée ? La variabilité des trajectoires augmente-t-elle avec l’accroissement de la longévité ? Pour répondre à ces questions, nous avons utilisé les données de l’enquête américaine Santé et Retraite (HRS). L’enquête HRS est une enquête portant sur un échantillon national d’individus âgés de 51 ans et plus, réalisée à l’aide du fichier de données RAND HRS. Il s’agit d’une version simplifiée et adaptée des données HRS collectées entre 1992 et 2008. Nous utilisons ici les données collectées de 1992 à 2004 pour l’échantillon de population blanche non hispanique (HRSw) comprenant 19 452 répondants. La durée moyenne d’observation était de 8,2 ans et la durée médiane de 8,9 ans. Pour cet article, les individus ont été classés selon les 3 états de santé suivants : en bonne santé (H), en incapacité (S) ou décédé (D). Un individu est considéré en incapacité s’il ou elle éprouve quelques difficultés à exécuter au moins une des activités de la vie courante (AVC) : traverser une pièce, s’habiller, se laver, manger, se coucher et se lever, et aller aux toilettes. Les décès sont extraits du fichier original HRS NDI_Death_tracker.sav. Le mois du décès est tiré du Registre national des décès (NDI). Il s’agit d’un registre national informatisé des décès compilé à partir des fichiers informatiques transmis au National Center for Health Statistics (NCHS) par les bureaux d’état civil de chaque État. Le NDI comprend la presque totalité des actes de décès aux États-Unis depuis 1979. La date du décès est basée sur le mois et l’année enregistrés dans le NDI et sur l’hypothèse d’un décès en milieu de mois[3]. La date de la transition entre les différents états d’incapacité correspond à la date de la vague à laquelle la transition a été enregistrée[4]. Les taux de transition (taux d’occurrence-exposition) sont indiqués ci-dessous à la figure 2. Aux âges plus avancés, la variation aléatoire des taux est forte du fait du nombre peu élevé d’individus. Les taux utilisés pour cet article ne sont pas lissés. Les taux de transition sont des taux par âge.

Figure 2

Taux de transition HRSw

H, en bonne santé ; S, en incapacité ; D, décédé.

Nous distinguons trois populations : la population de l’échantillon observé et deux populations virtuelles. La première population virtuelle a simplement une fonction de test de validité, tandis que la deuxième présente un véritable intérêt pour notre étude. La population virtuelle est une population synthétique parce que les histoires de vie des membres qui la composent sont fondées sur l’observation de plusieurs individus, en général à différentes étapes de leur vie. Lorsque le modèle de projection est bien spécifié et les paramètres sont fiables, on obtient une population synthétique très proche de la population réelle. Si la population synthétique est une représentation exacte de la population réelle, elle peut être utilisée pour déduire des informations complémentaires utiles et tester des hypothèses. La première population virtuelle s’obtient en associant à chaque individu de l’échantillon HRSw une contrepartie virtuelle. Pour cette contrepartie virtuelle, on utilise les taux de transition estimés à partir des données HRS pour produire une histoire de l’incapacité entre deux âges : l’âge de l’individu HRSw au début de l’observation, et son âge à la fin de l’observation. De cette façon, la population virtuelle recouvre exactement les mêmes tranches d’âge que l’échantillon de population HRSw, condition indispensable pour comparer la population virtuelle et la population réelle dans le cadre d’un test de validité. La microsimulation est exécutée à l’aide d’une fonction écrite en R et basée sur sim.msm. La fonction utilise l’ensemble des taux de transition par âge et simule un segment de vie entre deux âges différents, en commençant par un état donné pour l’âge le plus bas. Plusieurs indicateurs de la population virtuelle sont alors comparés à ces mêmes indicateurs pour l’échantillon de population HRSw afin de vérifier la validité de la microsimulation. Dans ces deux populations, les pourcentages des trajectoires d’incapacité sont comparables. Dans la population virtuelle, 55,4 % de la population est en bonne santé au début de l’observation et reste en bonne santé durant toute la période d’observation (56,2 % dans la population HRSw). Environ 10 % des individus présente une trajectoire HS et environ le même pourcentage une trajectoire HD.

La deuxième population virtuelle s’obtient en produisant pour chaque individu de cette population une histoire de vie de l’âge de 55 ans jusqu’au décès à l’aide des taux de transition estimés de la population HRSw indiqués en figure 2. On suppose que tous les individus entrent en observation à l’âge de 55 ans. La taille de la population virtuelle est considérée comme identique à celle de l’échantillon de population HRSw (19 452 individus). La répartition à 55 ans des individus en bonne santé et en incapacité est celle que l’on observe pour les HRSw : 17 974 en bonne santé et 1 478 en incapacité. La figure 3 montre la cohorte par âge et par statut d’incapacité. Le nombre d’individus en incapacité augmente, passant de 1 478 (7,6 %) à 55 ans à un maximum de 3 284 (41,0 % de survivants) à 87 ans. Au-delà de cet âge, ce nombre diminue du fait de la mortalité. La proportion de survivants en incapacité continue d’augmenter jusqu’à plus de 80 % à 90 ans et plus.

Figure 3

Population virtuelle de 55 ans et plus, par âge et statut d’incapacité

H, en bonne santé ; S, en incapacité ; D, décédé.

Les résultats de la microsimulation peuvent être comparés aux résultats d’une projection démographique. Le modèle de projection est similaire à l’équation (1) mais avec des taux par âge : k(t + 1) = P(t) k(t) = exp [- m(t)] k(t) où t désigne l’âge. L’équation peut aussi s’écrire k(t) = P(t- 1)P(t-2).... P(0) k(0).

La figure 4 indique, pour la cohorte des personnes âgées de 55 ans, la différence entre les valeurs de l’échantillon et les valeurs attendues du statut d’incapacité par âge. La microsimulation avec un échantillon de 10 000 individus produit des moyennes d’échantillon proches des valeurs attendues obtenues par le modèle démographique. Les différences sont peu marquées sauf pour les âges les plus avancés, lorsque la taille de l’échantillon est trop petite pour obtenir une estimation fiable des temps de séjour dans les différents états.

Figure 4

Projection de l’incapacité : comparaison du modèle à composantes de cohorte et de la microsimulation

H, en bonne santé ; S, en incapacité.

Mais le résultat le plus intéressant de la microsimulation, et ce qui justifie son utilisation en association avec la projection démographique, ce sont les trajectoires d’incapacité fournies par la projection démographique. Les trajectoires sont désignées par des lettres, par ex. HSD signifie en bonne santé, suivi d’un épisode d’incapacité et du décès. La plupart des personnes en bonne santé à l’âge de 55 ans meurent en bonne santé ou après un épisode isolé d’incapacité. On compte ainsi 26 % d’individus qui décèdent en bonne santé (HD) à l’âge de 74 ans en moyenne. Un nombre un peu plus élevé (28 %) décède après une première période d’incapacité (HSD) ; ils entrent en incapacité à l’âge de 77 ans et meurent cinq ans plus tard à 82 ans. La troisième trajectoire la plus fréquente est HSHSD (18 %). Les personnes suivant cette trajectoire entrent en incapacité à un âge inférieur (70 ans), guérissent 4 ans plus tard et entament une deuxième période d’incapacité à l’âge de 84 ans avant de décéder à 89 ans. Les personnes qui décèdent durant la période de guérison (HSHD) (13 %) meurent à un âge moins avancé (82 ans). Ces quatre trajectoires ont été suivies par 85 % de la cohorte en bonne santé à 55 ans. La microsimulation montre que les personnes en incapacité à 55 ans ont des chances de se rétablir, conclusion à laquelle nous serions également parvenus en vérifiant les taux de transition par âge. Seulement 14 % des individus meurent sans s’être rétablis ; ils meurent jeunes, à l’âge de 60 ans en moyenne. La guérison intervient le plus souvent vers 60 ans, indépendamment des trajectoires d’invalidité aux âges plus avancés. Ceux qui retrouvent la santé repoussent leur décès à un âge plus avancé. Les personnes qui décèdent durant la première période de rétablissement (SHD) (24 %) meurent à l’âge de 76 ans et ceux qui décèdent durant la deuxième période d’incapacité (SHSD) (26 %) entrent dans cette deuxième période d’incapacité à l’âge de 79 ans et meurent cinq ans plus tard à l’âge de 84 ans. Parmi les personnes en incapacité à 55 ans, 90 % connaissent l’une des cinq trajectoires d’incapacité suivantes : SHSD, SHD, SHSHSD, SD et SHSHD. Le taux élevé de rétablissement enregistré pour la population HRSw a deux conséquences majeures. Tout d’abord, le statut d’incapacité à 55 ans n’a pas un grand impact sur la trajectoire d’incapacité ultérieure. La trajectoire SHSD, par exemple, est à peine moins fréquente que la trajectoire HSD (26 % au lieu de 28 %). Cela se vérifie également pour la trajectoire SHD : 24 % en SHD et 26 % en HD. Les personnes qui se rétablissent après une période d’incapacité à l’âge de 55 ans connaissent toutefois d’autres transitions ultérieures environ deux ans plus tard. Ensuite, les études qui ne prennent pas les rétablissements en compte surestiment le nombre d’années prévues en incapacité. Les rétablissements sont omis lorsqu’on utilise un modèle maladie-décès plutôt qu’un modèle multi-états complet.

Conclusion

Le modèle le plus utilisé dans les projections de population est le modèle à composantes de cohorte. L’âge et les attributs personnels sont utilisés pour segmenter la population en sous-groupes exposés de manière différentielle aux risques de la fécondité, de la mortalité et de la transition vers un autre sous-groupe. Un des principaux atouts du modèle à composantes de cohorte est qu’il explique le fait que, dans une population, les niveaux d’exposition et de risque varient avec l’âge et les attributs personnels tels que le statut d’incapacité, le sexe, la situation professionnelle, etc. Le résultat obtenu à l’aide du modèle à composantes de cohorte consiste le plus souvent en un nombre d’individus à une date future réparti en sous-groupes. Il est possible d’extraire davantage d’informations sur la population future à partir du modèle et de ses paramètres. La durée prévue de séjour dans le sous-groupe est un indicateur utile. La répartition des durées de séjour dans les sous-groupes en est un autre. La durée prévue peut être obtenue très facilement de manière analytique, à condition d’utiliser les taux par âge selon l’usage habituel. Les formules sont indiquées dans le présent article. La méthode à utiliser est avant tout la table de vie multi-états appliquée tout au long du parcours de la cohorte. La distribution des durées de séjour peut être obtenue par la microsimulation. Les durées de séjour sont associées aux taux de transition de manière aléatoire et non déterministe. La microsimulation constitue une aide pour mettre en évidence les effets du hasard. Elle constitue également une technique permettant d’identifier des parcours de vie cohérents avec les taux de transition empiriques. Les taux de transition empiriques par âge impliquent une probabilité plus grande de certains parcours de vie par rapport à d’autres. Les parcours de vie révélés par les séries de taux de transition et la probabilité de réalisation de chacun de ses parcours constituent des informations utiles qui viennent compléter les informations relatives aux nombres d’individus par sous-groupe à des dates futures déterminées. En général, ces informations ne peuvent être obtenues que par la microsimulation.

La microsimulation devrait produire des résultats cohérents avec ceux du modèle à composantes de cohorte. Pour que ces résultats soient totalement cohérents, il est nécessaire d’utiliser les mêmes taux de transition. En conséquence, le nombre de sous-groupes définis dans la microsimulation ne doit pas être supérieur à celui du modèle à composantes de cohorte. Cela implique également que les effets des covariants doivent être traités de la même façon avec ces deux méthodes. Le recours à la microsimulation se justifie souvent parce qu’elle permet d’obtenir des informations plus détaillées que les modèles démographiques. Cet objectif n’est pas incompatible avec le critère de cohérence. Toutefois, si la microsimulation prend en compte une plus grande variabilité des taux de transitions que la méthode des composantes, c’est-à-dire qu’elle prend en compte une population plus hétérogène, alors les résultats de la microsimulation et du modèle à composantes ne sont plus identiques.

La méthode des composantes remonte à Cannan (1895) mais est habituellement associée à Whelpton (1928). C’est pratiquement la seule méthode employée par les démographes pour obtenir des projections de population. La microsimulation, quant à elle, est apparue dans les années 1960, avec la mise au point par Orcutt d’un modèle de population complet (Orcutt, Caldwell et Wertheimer, 1976). Cinquante ans plus tard, la microsimulation connaît un regain de popularité (Zaidi, Harding et Williamson, 2009). Il est temps aujourd’hui d’intégrer la microsimulation dans les modèles démographiques afin de déceler des schémas qui échappent habituellement à l’observation.

Notes

• [1] Dans ce cas, la matrice m est singulière et par conséquent elle ne peut être inversée. Pour obtenir une estimation du temps de séjour prévu total dans les différents états fonctionnels avant un instant futur t, on ajoute un très petit nombre aux éléments diagonaux de m. Ce petit nombre peut être interprété comme un très faible taux de sortie vers un état absorbant qui n’est pas inclus dans l’espace de l’état (p. ex, décès). Le temps d’attente prévu avant l’entrée dans un état absorbant est supérieur à 1 divisé par ce petit nombre, ce qui correspond à un nombre très important qui n’affecte pas vraiment le temps de séjour total prévu dans les états fonctionnels pendant la période de 0 à t. Ici, nous avons utilisé le nombre 1e-08 (0,00000001).
• [2] La simulation à événements discrets est utilisée dans le cadre du projet MicMac, qui vise à combler l’écart micro-macro dans les projections de population. Pour une description du logiciel MicMac, voir l’annexe A.
• [3] Pour les besoins de l’analyse, toutes les dates (date de naissance, date du décès, date des vagues) ont été converties en dates SAS. Les dates SAS mesurent le nombre de jours écoulés depuis le 1er janvier 1960. Elles sont converties en années et fractions d’année à l’aide de la formule suivante : dateyr < - dateSAS/365,25 + 1960.
• [4] Cette procédure surestime l’âge à la transition de l’état sans incapacité à l’état d’incapacité mais également de l’état d’incapacité à l’état sans incapacité. Un nombre très important d’individus étant en incapacité au début de l’observation, la procédure ne devrait pas trop affecter les résultats.