Abstracts
Résumé
En faisons-nous assez pour les générations futures? Cette question est sous-jacente à de nombreuses questions économiques actuelles, comme celles de la réduction de la dette, de la réforme des retraites, de la lutte contre le changement climatique, de la préservation des ressources naturelles, des investissements d’infrastructure ou de la fiscalité de l’épargne par exemple. Notre responsabilité sociale envers les générations futures se traduit en termes économiques par le taux d’actualisation, qui donne une valeur au futur relativement au présent, et qui détermine l’arbitrage présent/futur des agents économiques. Si on reconnaît qu’une société court-termiste utilise un taux d’actualisation trop élevé, comment déterminer le niveau désirable de ce taux? Dans cet article, je synthétise les importants développements scientifiques récents sur ce sujet. Étant donné la baisse tendancielle de nos anticipations de croissance et les fortes incertitudes sur les évolutions longues de notre société, je recommande un taux sans risque de deux fois le taux de croissance anticipé de la consommation (pour actualiser des cash flows engendrés sur les horizons inférieurs à 20 ans) à 1 % (pour des maturités au-delà de 100 ans). La prime de risque devrait aussi avoir une structure par terme, s’étalant de 1 % à court terme jusqu’à 3 % pour le long terme.
Abstract
Do we do enough for the future? This question is related to many different current issues, from the reduction of sovereign debt in Europe, to the pension reform, the fight against climate change, the preservation of natural resources, the level of public investment in infrastructure, or the fiscal treatment of long-term savings for example. Our social responsibility towards future generations is decentralized through the choice of the discount rate, which determines the tradeoff between present sacrifices and future benefits. How should we define the efficient level of long-termism? In this paper, I summarize the most important evolutions in the economic analysis of this question in recent years. Given the strong uncertainties that prevail concerning the long term evolution of our society, I recommend to use a discount rate ranging from 2 times the anticipated growth rate of consumption for short time horizons, going down to 1 % for time horizons above 100 years. The systematic risk premium should also have a term structure, starting at around 1 % for short maturities to 3 % for extra-long ones.
Article body
Introduction
Le destin des civilisations, de leur émergence à leur écroulement, dépend de leur capacité à maintenir une préoccupation pour l’avenir par rapport à la satisfaction des besoins immédiats. Une myriade de décisions individuelles et collectives traduisent concrètement ces préoccupations, depuis l’accumulation du capital par l’épargne longue et les investissements, jusqu’au niveau d’éducation, en passant par la préservation de l’environnement, l’exploitation des ressources naturelles, la qualité des infrastructures publiques, et l’intensité des efforts de recherche et développement. Dans son livre Collapse : How Societies Choose to Fail or Succeed, Jared Diamond (2005) décrit une civilisation florissante installée sur l’île de Pâques jusqu’à la veille de sa découverte par les Occidentaux, et qui s’écroule avant leur arrivée par son incapacité à empêcher la surconsommation d’une ressource naturelle pourtant essentielle à sa survie, le bois. La crise de la pomme de terre en Irlande sur la période 1846-1850 offre une autre illustration cataclysmique du manque de préoccupation pour l’avenir. Plus d’un million d’Irlandais y laissèrent la vie. L’absence d’épargne de précaution au niveau individuel et la faiblesse du stockage de denrées non périssables au niveau collectif, constitue une des explications de la catastrophe.
La publication en 1972 du livre intitulé The Limits to Growth par le Club de Rome marque l’émergence d’une conscience collective envers les périls associés à un développement non durable. Depuis, le citoyen, le politicien, l’entrepreneur et l’actionnaire ont dû affronter une liste grandissante de problèmes environnementaux qui inclut la gestion des déchets nucléaires, la raréfaction des ressources naturelles, la perte de biodiversité ou la pollution des airs, de la terre et des océans. Le cas de l’augmentation de la concentration des gaz à effet de serre et les modifications climatiques qui s’ensuivent constitue un exemple particulièrement prégnant. Ces problèmes environnementaux posent tous la même question : en faisons-nous trop ou pas assez pour les générations futures? Cette question transcende les sujets environnementaux. Elle est centrale dans de nombreux sujets de politique publique, comme la réforme des pensions, le niveau approprié de dette publique, les investissements dans les infrastructures publiques et les efforts dans le domaine de l’éducation et de la R&D.
Les décideurs publics ne sont pas les seuls à être confrontés aux risques environnementaux de long terme. Les marchés financiers sont traditionnellement taxés de court-termisme. De nombreuses entreprises et épargnants désirent néanmoins contribuer à un développement plus respectueux des intérêts des générations futures. L’émergence de fonds labellisés « Investissement socialement responsable » (ISR) illustre cette évolution encore embryonnaire, dans laquelle les règles d’allocation d’actifs des fonds intègrent d’une façon ou d’une autre des impacts à long terme des investissements qu’ils financent. Des agences de notation sociale et environnementale ont été créées pour évaluer les actifs des entreprises sous cet angle. Néanmoins, cette dynamique n’a pas encore permis d’établir un consensus sur les outils opérationnels permettant d’intégrer les impacts de long terme dans l’évaluation des actifs financiers. Jusqu’à présent, l’absence de transparence dans les méthodologies utilisées par les fonds ISR a clairement limité le développement de ces produits financiers. Dans ce contexte aussi, les économistes sont appelés avec d’autres sciences humaines et sociales à poser les termes du débat relatif à la question de l’intensité de nos efforts envers les générations futures.
Depuis que l’homo sapiens a émergé comme l’espèce dominante sur notre planète, et jusqu’à très récemment, les êtres humains consommaient chaque année ce qu’ils glanaient, chassaient où récoltaient durant l’année. Sous la férule de la loi de Malthus, l’humanité semble être restée au niveau de subsistance durant des milliers de générations. Malgré les développements récents sur les notions d’incohérence dynamique et d’actualisation hyperbolique (voir par exemple Strotz, 1956 et Laibson, 1997), il est incontestable que les êtres humains, contrairement à la plupart des autres espèces, ont la conscience de leur propre futur, aux niveaux individuel, dynastique, communautaire et anthropologique. Au niveau individuel, l’être humain établit des compromis entre la satisfaction de ses besoins immédiats et ses aspirations pour une vie meilleure à l’avenir. Jeune, il investit dans son capital humain. Plus tard, il épargne pour sa retraite. Il fait des efforts pour préserver sa santé en faisant du sport, en se brossant les dents ou en mangeant sainement. Il planifie son propre futur et celui de ses enfants auxquels il désire transmettre du bien souvent hérité de ses propres parents. Une fois le droit de propriété individuel clairement protégé (graduellement à partir de la fin du Moyen Âge en Europe), les aspirations individuelles aux investissements d’avenir furent débloquées. En parallèle, les États ont lentement pris conscience de leur rôle en tant que producteur de biens publics durables, comme les infrastructures routières, les écoles ou les hôpitaux. Au niveau agrégé, cela a conduit à une gigantesque accumulation de capital physique et intellectuel, qui a engendré la croissance économique et la prospérité, comme décrit dans la théorie néoclassique de la croissance (Solow, 1956). Avec une croissance économique de 2 % par an, nous consommons aujourd’hui 50 fois plus de biens et services qu’il y a 2 siècles. Ce sont les sacrifices des générations passées qui ont rendu ce phénomène prodigieux possible.
L’observation de cette dynamique pose une question cruciale : en faisons-nous trop ou pas assez pour les générations futures? Plutôt que d’investir, ne devrions-nous pas consommer? Selon la formule consacrée, au lieu de dépenser à fonds perdus pour la conquête spatiale, ne devrions-nous pas sortir les plus pauvres des affres de la malnutrition, de la misère, de l’analphabétisme, de la malaria et du sida? Lomborg (2004) répond par l’affirmative à travers son « consensus de Copenhague », mais la communauté des économistes reste divisée sur ce point.
Dans des sociétés décentralisées comme la nôtre, la préoccupation pour l’avenir qu’ont la myriade d’agents économiques est coordonnée par la fixation d’une unique variable, le taux d’intérêt ou taux d’actualisation. On peut longtemps disserter sur les comportements responsables ou irresponsables des uns et des autres, mais en fin de compte, les décisions des ménages, des entreprises, des investisseurs et de l’État seront toujours déterminées par le taux d’actualisation, variable socioéconomique cruciale de notre dynamique économique. Comme l’écrivait William Baumol en 1968 :
Il y a peu de sujets dans notre discipline qui peuvent rivaliser avec celui du taux d’actualisation pour le degré considérable de connaissances accumulées et simultanément pour le niveau substantiel d’ignorance résiduelle.
Baumol, 1968
Le corollaire de cette observation qui reste d’actualité, c’est que beaucoup de commentateurs continuent à proclamer que les acteurs économiques et les marchés financiers sont court-termistes, sans que les économistes puissent exprimer une opinion scientifiquement fondée pour contribuer à ce débat. Dans cet article, j’essaie de construire un fondement scientifique à cette question.
1. Actualisation appliquée
La plupart de nos actes ont des effets qui sont disséminés dans le temps et dans de multiples dimensions sanitaires, financières et environnementales. Par exemple, lutter contre le changement climatique engendre des coûts financiers immédiats (investissement dans les énergies non fossiles et l’isolation, obsolescence accélérée des centrales thermiques…) et extra-financiers (perte de temps dans les transports en commun, réallocation de l’utilisation des terres…) ainsi que des bénéfices futurs, financiers (réduction des dommages aux biens…) et extra-financiers (amélioration de la biodiversité, augmentation de l’espérance de vie…). Confrontés à l’immensité des actions possibles pour améliorer le futur, il est indispensable de disposer d’une boîte à outils simple, transparente et opérationnelle pour déterminer si ces actes sont désirables au niveau de la communauté des parties prenantes, impliquant le cas échéant les générations futures. L’analyse coût-bénéfice (ACB) constitue un ensemble cohérent permettant d’établir une liste d’actions prioritaires compatibles avec l’intérêt général. Sa mise en place nécessite de fixer un ensemble de valeurs (ou prix) permettant de monétariser les effets extra-financiers. Ainsi, on devra se mettre d’accord sur la valeur d’une année de vie en bonne santé, ou des actifs environnementaux (valeur d’usage de la forêt, de l’ours des Pyrénées, du silence…). La manière de déterminer ces valeurs dépasse les objectifs de cet article. Retenons seulement qu’il est crucial que tous les agents économiques utilisent le même jeu de valeurs pour évaluer l’ensemble des actions à leur disposition.
Il existe un prix particulièrement difficile à déterminer et qui fait l’objet d’une bruyante controverse depuis une vingtaine d’années dans le microcosme des économistes de l’environnement. C’est celui du prix du temps. Disposer d’un euro immédiatement a plus de valeur que de n’en disposer que dans un an. Le taux auquel on déprécie une variation donnée de consommation s’appelle le taux d’actualisation. Pour évaluer un projet dont les coûts et les bénéfices sont étalés dans le temps, on calcule la somme de ces flux actualisés à ce taux. Si cette valeur actualisée nette (VAN) est positive, ce projet devrait être réalisé. Pour que cette règle de décision soit optimale, un simple argument d’arbitrage suggère que le taux d’actualisation doit être égal au taux de rendement des investissements sans risque dans l’économie ou taux d’intérêt[1].
Un taux d’actualisation positif déprécie l’avenir. C’est particulièrement vrai pour des horizons éloignés. Ainsi, un kilo de riz dans 100 ans actualisé à 4 % a une valeur présente égale à 1000/1,04100 = 20 grammes de riz. Ceci signifie qu’une action dont le seul effet à l’avenir est d’offrir un kilo de riz dans un siècle ne devrait être entreprise que si elle implique un sacrifice immédiat inférieur à 20 grammes de riz. Un taux trop élevé conduit à une évaluation qui dévalorise trop l’avenir par rapport au présent, et devra être considérée comme court-termiste. Mais quelle signification devons-nous donner à un taux « trop élevé »?
L’importance de cette question peut être illustrée dans le cadre du changement climatique. Nordhaus (2008) utilise un taux d’actualisation de 5 % pour estimer la valeur présente du flux de dommages futurs (financiers et extra-financiers) induits par l’émission d’une tonne de CO2 (tCO2) de plus aujourd’hui, dans l’hypothèse de l’absence d’intervention publique pour réduire ces émissions. Il obtient une valeur actuelle de huit dollars. Cela signifie qu’aucune action de réduction des émissions de CO2 ne devrait être entreprise qui coûte plus de huit dollars par tonne de CO2 évitée. Si on désire décentraliser les efforts de réduction, Nordhaus recommanderait donc une taxe écologique de huit dollars par tonne de CO2 émise. Dans ces conditions, la plupart des projets environnementaux tels que la séquestration, l’éolien, le photovoltaïque ou les biocarburants ont une valeur actualisée nette négative, c’est-à-dire qu’ils détruisent de la valeur puisque leurs sacrifices immédiats, que leur mise en oeuvre exige, sont supérieurs à la valeur actuelle des bénéfices futurs. Nordhaus conclut que la meilleure réponse au challenge climatique n’est pas d’investir massivement en utilisant les technologies actuelles, mais plutôt d’investir dans la R&D avant de réduire les émissions une fois les technologies efficaces obtenues, le cas échéant. Stern (2007) utilise plutôt un taux d’actualisation de 1,4 %, bien plus faible que celui de Nordhaus[2]. Étant en conséquence plus long-termiste, il obtient une valeur présente des dommages futurs d’une tCO2 bien supérieure, autour de 85 dollars. Avec une telle valeur pour les tCO2 évitées, de nombreuses technologies vertes deviennent socialement désirables et individuellement profitables si une taxe de 85 dollars par tCO2 évitée était imposée au niveau de la planète. Il augmenterait les sacrifices demandés aux générations actuelles.
Le niveau du taux d’actualisation pour évaluer les projets d’investissement publics fit l’objet d’importants débats dans les années soixante et soixante-dix dans la plupart des pays occidentaux. Aux États-Unis, l’origine des débats a pour origine l’article de Krutilla et Eckstein (1958) dans le secteur de la gestion de l’eau, mais ce débat se généralisa rapidement aux autres secteurs, comme l’énergie, les transports et la protection de l’environnement. Dans d’autres pays comme la France avec ses plans quinquennaux, des taux d’actualisation ont été fixés pour évaluer les politiques et investissements publics. Leurs niveaux et évolutions dans le temps sont résumés dans l’encadré 1.
En tant qu’observateur, acteur, et président de très nombreuses réunions de travail dans les ministères et dans les entreprises durant les deux dernières décennies en France, je peux témoigner des intenses débats et des tractations qui fondent ces décisions. Alors que les opérateurs privés qui construisent les infrastructures publiques et les ministères qui les encadrent (transport, équipement, agriculture, écologie, santé…) sont en général favorables à une baisse du taux d’actualisation parce que cela augmente la VAN des projets qu’ils soutiennent, le ministère des Finances se trouve en travers de leur chemin précisément parce qu’une baisse du taux d’actualisation peut augmenter massivement les besoins de financement public pour ces projets, dans un contexte financier particulièrement contraint. Jusqu’à présent, force est de constater que les chercheurs ont pu arbitrer efficacement ces conflits. S’ils sont intenses, c’est parce que la baisse du taux a un énorme impact sur l’évaluation de projets cruciaux pour certains ministères, comme le renforcement des infrastructures routières et ferroviaires (TGV, tunnel Lyon-Turin…), la politique d’investissement dans le secteur électrique (renouvellement du parc nucléaire et du réseau de transport, tarif de rachat…) ou la détermination du niveau d’une hypothétique taxe sur les émissions de carbone.
La littérature économique offre un corpus très riche pour réfléchir au niveau auquel ce taux d’actualisation devrait se trouver. La théorie moderne de la finance, qui cherche à donner une valeur aux actifs et aux investissements, constitue la référence épistémologique naturelle à ces réflexions. Des milliers d’articles ont été écrit à ce sujet. Néanmoins, on ne peut pas dire que cette intense activité de recherche ait permis de faire émerger un consensus dans la profession au sujet du taux d’actualisation, comme le montre Weitzman (1998).
Graphique 1
Histogramme des estimations individuelles du taux d’actualisation dans un échantillon de 2 160 économistes du monde académique
2. Les taux d’actualisation comme coût d’opportunité du capital sans risque
Une des difficultés soulevées par la littérature récente sur le taux d’actualisation provient de la multiplicité des approches pour l’estimer. Dans un monde parfait, il y a en effet trois façons de déterminer le taux d’actualisation socialement désirable. En effet, dans un tel monde sans friction, ce taux est égal à la fois au taux de rendement du capital privé sans risque, au taux d’intérêt du marché et au taux auquel les ménages sont prêts à substituer la consommation présente à la consommation future.
J’ai déjà expliqué pourquoi le taux d’actualisation doit être égal au taux de rendement du capital privé sans risque. Supposons qu’un investissement marginal de 100 dans l’économie rapporte 104 dans un an, c’est-à-dire que le rendement du capital est de 4 %. Dans ce cas, divertir du capital pour investir dans un projet public dont le taux de rendement interne (TRI) est inférieur à 4 % détruirait de la valeur sociale. Le taux d’actualisation reconnaît donc un coût d’opportunité social au capital. Notons que demander que le TRI d’un projet soit supérieur au taux d’actualisation est équivalent[5] à demander que la VAN du projet calculée avec ce taux soit positive.
Si les marchés financiers sont parfaits, le taux d’intérêt d’équilibre est égal au taux de rendement du capital marginal dans l’économie. En effet, les entrepreneurs vont emprunter pour investir tant que le TRI de leur projet est supérieur au taux d’intérêt auquel ils empruntent. La productivité marginale du capital étant décroissante, l’optimum sera atteint quand TRI et taux d’intérêt s’égalisent finalement. Le taux d’intérêt d’équilibre révèle donc le coût d’opportunité du capital dans l’économie. Ce signal-prix devient le coût moyen pondéré du capital (CMPC, ou WACC en anglais) que vont utiliser tous les entrepreneurs sans risque pour déterminer leur stratégie d’investissement.
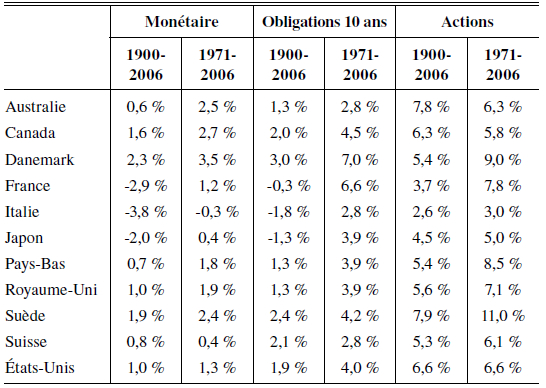
Ainsi émerge une idée simple de cette analyse : pour atteindre l’optimum social, il suffit d’utiliser le taux d’intérêt du marché pour actualiser les flux des projets d’investissement sans risque. Dans le tableau 1, j’ai calculé le taux de rendement réel annualisé du marché monétaire et des obligations d’État à 10 ans pour différents pays, respectivement sur les périodes 1900-2006 et 1971-2006. Sur l’ensemble du siècle écoulé, ce taux d’intérêt moyen fut de -2,9 % (pour le monétaire) et de -0,3 % (pour les obligations à 10 ans) en France, ce qui correspond au fait historique bien connu de « l’euthanasie du rentier » par les vagues successives d’inflation qui ont laminé les rendements réels des actifs à revenus (nominaux) fixes. Ce fait historique se retrouve dans tous les pays qui ont connu une guerre mondiale sur le territoire. Pour les autres, on constate un taux d’intérêt réel moyen autour de 1 % (pour le monétaire) et de 2 % (pour les obligations à 10 ans) sur l’ensemble du siècle. Si on se concentre sur la période plus récente 1971-2006, ce taux d’intérêt réel fut bien supérieur, pour les deux types d’actifs sans risque.
Tableau 1
Rendements réels annualisés des actifs financiers
On entend souvent l’idée selon laquelle les marchés financiers exigeraient une rentabilité minimum de 15 % des actifs. Selon cette idée, les investisseurs utiliseraient un taux d’actualisation de 15 % pour évaluer les différentes classes d’actifs dans leur portefeuille. Si c’était vrai, ceci constituerait un court-termisme extrême. Le tableau 1 montre clairement que cette rumeur est fausse, en tout cas pour la classe d’actifs peu risqués que sont les obligations d’État à 10 ans. Dans ce même tableau, j’ai aussi calculé sur les mêmes périodes et pour les mêmes pays, le taux de rendement réel annualisé d’un portefeuille diversifié d’actions. On peut conclure de ces données que ce taux de 15 % est un fantasme inassouvi même pour les détenteurs d’actions, puisque le rendement réel annualisé des actions entre 1900 et 2006 ne fut que de 3,7 % en France et 6,6 % aux USA.
Comme on l’a vu dans la section précédente, les opérateurs publics ont parfois dans le passé justifié l’utilisation d’un taux d’actualisation élevé par l’observation d’un rendement important du capital privé, par eux interprétés comme celui des actions. Je rappellerais ici que j’ai défini le taux d’actualisation comme le prix du temps, c’est-à-dire celui justifié par le fait de percevoir un bénéfice certain à l’avenir plutôt qu’aujourd’hui. Si ce bénéfice futur devient aussi incertain, on introduit une autre caractéristique de différenciation que le temps. Cette caractéristique, le risque, doit être valorisée en tant que telle et de façon indépendante du prix du temps. En théorie de la finance, il s’agit de la prime de risque, calculée comme la différence avec le rendement espéré du portefeuille diversifié contenant l’ensemble des actifs risqués. Le taux d’actualisation discuté ici est donc celui qu’il faut utiliser pour évaluer les seuls projets sans risque. Le rendement réel des actions, dont on sait qu’ils constituent une classe d’actifs très risqués, ne peut être utilisé comme référence pour ce taux d’actualisation, puisqu’il contient cette prime de risque en supplément du prix du temps.
Du côté des consommateurs, le taux d’intérêt est le taux auquel ils peuvent prêter ou emprunter pour transférer de la consommation dans le temps. Ce taux d’intérêt décrit donc aussi le taux minimum de rentabilité de l’épargne que les ménages exigent pour accepter de sacrifier leur consommation présente pour augmenter leur consommation future (taux marginal de substitution intertemporelle : TMSI). Investir dans un projet dont le TRI est supérieur au TMSI accroît le bien-être des ménages. Il est donc socialement désirable que le taux d’actualisation soit égal à la fois au taux d’intérêt et au taux marginal de substitution intertemporelle des ménages.
Dans une économie sans friction, c’est bien ce qu’il se passe : le taux d’intérêt révèle à la fois le coût d’opportunité du capital et l’exigence de rendement pour que les ménages acceptent de sacrifier un petit peu de leur consommation présente au bénéfice de l’avenir. L’équilibre concurrentiel que cette égalité caractérise engendre une allocation intertemporelle efficace des ressources, dans le sens où il conduit à un bien-être intertemporel maximal pour l’agent représentatif. L’utilisation de ce prix du temps dans l’évaluation des projets par les ménages et les entreprises décentralise les décisions de façon efficace. Néanmoins, nous savons que nos économies sont confrontées à de multiples sources de friction. Elles conduisent à une inefficacité de l’allocation des ressources et à un taux d’intérêt d’équilibre qui n’est plus le bon signal-prix que les agents devraient utiliser pour déterminer leurs actions d’épargne et d’investissement. Deux grandes familles de friction peuvent être identifiées.
Les problèmes d’agence. Le financement des investissements des entreprises et des particuliers est rendu difficile par le fait que les prêteurs ont en général une moins bonne information sur les capacités de remboursement des emprunteurs (solvabilité). Les problèmes d’antisélection et de risque moral que cela engendre sur les marchés financiers (bulle des subprimes, bulle Internet, crise des dettes souveraines…) sont très importants, comme le suggère, par exemple, la répétition des crises auxquelles ces marchés sont confrontées. Outre les importantes inefficacités dans l’allocation du capital dans l’économie, ces problèmes provoquent des distorsions dans les prix de marché.
Les problèmes intergénérationnels. Comme le souligne Diamond (1977), les générations futures ne peuvent évidemment pas échanger avec les générations présentes. Leurs intérêts ne peuvent pas s’exprimer sur les marchés. S’ils le pouvaient, ils emprunteraient et investiraient une partie des richesses produites aujourd’hui, mais leur incapacité à rembourser ces emprunts dans un laps de temps qui intéresse les générations actuelles rend le contrat impossible. Si une accumulation de capital se produit, c’est parce que les jeunes anticipent qu’ils doivent accumuler des actifs qu’ils pourront revendre ultérieurement pour financer leur retraite, et aussi, peut-être, parce qu’ils éprouvent un peu d’altruisme envers leurs descendants et désirent leur transmettre un capital. Mais cet altruisme intergénérationnel est probablement insuffisant pour que le taux d’intérêt reflète autre chose que le seul intérêt des générations actuelles.
J’en conclus que la seule observation du prix de marché du temps ne nous permet pas de déterminer le taux d’actualisation optimal du point de vue de la communauté de toutes les générations présentes et futures. Le taux d’intérêt et le taux de rendement du capital privé sans risque ne nous donnent qu’une information biaisée concernant la valeur que la société accorde au report de la satisfaction du désir de consommation dans un temps plus éloigné.
3. Définition de l’intérêt général dans une perspective intergénérationnelle
Comment définir un niveau optimal de sacrifice du présent en faveur du futur? Pour déterminer un optimum, il faut commencer par définir un objectif. Un objectif intergénérationnel possible serait de maximiser le bien-être de la génération la moins favorisée, mais cette approche rawlsienne est très rarement retenue par les économistes[6]. L’approche traditionnelle étudiée par Samuelson (1937) et axiomatisée par Koopmans (1960) est dénommée « modèle de l’espérance d’utilité actualisée ». Dans cette approche utilitariste, l’objectif retenu est la maximisation du flux actualisé de l’espérance d’utilité des différentes générations. Chaque génération extrait du bien-être des biens et services qu’elle consomme. Le niveau de consommation est synthétiquement mesuré par le PIB par habitant. On suppose que le bien-être (ou utilité) est une fonction croissante et concave de ce niveau de consommation. La concavité de cette fonction d’utilité est cruciale. Elle signifie que l’utilité marginale de la consommation est une fonction décroissante de cette consommation. En d’autres termes, une unité de consommation supplémentaire a un effet sur le bien-être plus important si elle est allouée à un pauvre plutôt qu’à un riche. Ce principe d’utilité marginale décroissante caractérise donc dans ce contexte interpersonnel une préférence pour la réduction des inégalités, c’est-à-dire une aversion aux inégalités.
Comme une politique publique ou un projet d’investissement engendrent des générations gagnantes et des générations perdantes, il est nécessaire de déterminer comment pondérer ces gains et ces pertes d’utilité pour orienter la décision collective. Dans l’approche utilitariste, on se limite à calculer une somme actualisée des variations d’utilité des différentes générations. Le taux auquel on actualise les utilités des générations futures est un taux de préférence pour les générations présentes. Il caractérise notre attitude éthique vis-à-vis du futur, ou, à l’inverse, notre degré d’égoïsme. Pour des raisons éthiques évidentes, je propose de fixer ce taux de préférence pour le présent à zéro. Ceci signifie que je définis le taux d’actualisation comme celui qui permet de soutenir une allocation des ressources qui maximise la somme (non pondérée) des espérances d’utilité des générations présentes et futures. L’absence de pondération dans la définition de l’intérêt général signifie qu’on ne donne aucune primauté aux différentes générations selon leur ordre de naissance.
Plusieurs arguments ont été présentés dans la littérature pour justifier cette approche utilitariste de l’éthique intergénérationnelle. Celle qui me plait le plus est l’argument rawlsien du voile d’ignorance, qui est la base de l’approche utilitariste (Harsanyi, 1955). Imaginons que nous puissions réunir toutes les générations à venir au sein d’une instance qui devrait choisir l’allocation des richesses de la planète d’ici la fin des temps. Les membres de cette instance représentative sont sous le voile d’ignorance, c’est-à-dire qu’aucun d’eux ne sait encore dans quelle génération il va prendre place. Dans ce contexte, créer plus d’inégalité entre générations, c’est augmenter les risques pour les individus encore dans les limbes. En fait, ces derniers se représenteront le problème comme une décision en incertitude. Le modèle d’espérance d’utilité constitue alors dans ce cadre un critère de décision dont les fondements axiomatiques sont attractifs d’un point de vue normatif. Or, si on accorde une même probabilité à naître dans telle ou telle génération, l’espérance d’utilité est juste proportionnelle à la somme des utilités, ce qui implique que les individus dans les limbes voteront unanimement en faveur de l’allocation intertemporelle qui maximise la somme des utilités espérées. Il faut noter ici que la concavité de la fonction d’utilité caractérise l’aversion au risque des agents sous le voile d’ignorance. L’aversion aux inégalités de notre société est justifiée par l’aversion au risque des générations futures sous le voile d’ignorance.
Une autre justification de l’approche utilitariste est une forme extrême de l’altruisme intergénérationnel dans laquelle les générations intégreraient le bien-être des générations futures comme si c’était la leur. Imaginons que chaque parent extraie autant de bonheur à voir ses descendants consommer des biens et services dans l’avenir que si c’était ce parent qui les consommait lui-même. Cet altruisme dynastique gomme la nature intergénérationnelle du problème intertemporel. Si on reconnait qu’un individu évalue son bien-être intertemporel comme la somme des utilités à chaque période de la vie (ici la sienne et celles de ses descendants)[7], on retombe bien sur le modèle utilitariste. Il faut noter ici que la concavité de la fonction d’utilité caractérise une aversion aux inégalités intertemporelles ou intergénérationnelles.
4. La règle de Ramsey
Dans ce modèle apparaît un argument évident pour valoriser les bénéfices futurs de moindre façon que les bénéfices présents. Supposons que nous anticipions un maintien d’une croissance positive. Puisqu’investir dans ce contexte revient à déshabiller la pauvre génération actuelle pour habiller la riche génération future, une telle action accroît les inégalités intergénérationnelles. Nous ne devrions considérer cette action comme socialement désirable que si le coût social de cette redistribution à l’envers est plus que compensé par une rentabilité suffisamment élevée de l’investissement. En d’autres termes, dans un monde en croissance, le taux d’actualisation peut être interprété comme le TRI minimum d’un investissement qui compense l’impact négatif de cet investissement sur les inégalités intertemporelles. Rappelons qu’avec un taux de croissance réel de la consommation de 2 % par an, nous consommons aujourd’hui 50 fois plus de biens et services qu’à l’époque napoléonienne. Si on anticipe le maintien de cette croissance, la problématique du changement climatique revient à s’inquiéter du bien-être de gens qui, dans 200 ans, bénéficieront d’un PIB par habitant 50 fois supérieur au nôtre. Sous cet angle, lutter contre le changement climatique, c’est comme demander des sacrifices aux sans-abris pour enrichir Bill Gates!
Techniquement, cet effet est relié à l’objectif de bien-être intergénérationnel décrit dans la section 3 par le biais de l’hypothèse d’utilité marginale décroissante avec la richesse. Le niveau de consommation étant croissant avec le temps, l’utilité marginale de cette consommation sera plus faible à l’avenir. Dans un tel contexte, réduire la consommation aujourd’hui pour augmenter la consommation demain d’un même montant réduit le bien-être intertemporel puisqu’un tel transfert réduit plus l’utilité d’aujourd’hui qu’il n’augmente l’utilité de demain.
Reste à quantifier cet effet. On aura compris qu’il est croissant avec la vitesse à laquelle l’utilité marginale décroît quand la consommation augmente, et avec le taux de croissance de la consommation. La vitesse à laquelle l’utilité marginale décroît quand la consommation croît est appelée dans la suite « coefficient γ ». Son estimation dépend de l’interprétation qu’on donne à cette caractéristique de la fonction d’utilité. Cette aversion aux inégalités est de nature éthique, et l’économiste ne peut que suggérer une méthode pour que la société le choisisse. Par exemple, on peut mener le test par introspection suivant. Supposons que nous vivions dans une société avec deux classes sociales de même taille. Supposons aussi que la classe supérieure soit deux fois plus riche que la classe inférieure. Imaginons une politique de redistribution des riches vers les pauvres avec des déperditions, dans le sens où une partie des sommes collectées chez les riches s’évapore sur le chemin du transfert[8]. Dans un tel contexte, cette politique redistributive n’est désirable que si le bénéfice social de la réduction des inégalités l’emporte que son coût social provenant de ces pertes. D’après vous, quelle est la perte maximale par euro collecté chez les riches compatible avec cette politique? Si on n’a aucune sensibilité aux inégalités, le coefficient γ est par définition nul, et la réponse doit être de 0 euro. Si on a de l’aversion aux inégalités, on peut tolérer une certaine déperdition positive. Intuitivement, plus l’aversion aux inégalités est importante, plus la perte maximale acceptable est élevée. Dans le tableau 2, j’ai calculé le lien entre cette perte maximale et le coefficient γ[9]. Si on considère que cette perte maximale est comprise entre 50 et 75 centimes, on devrait utiliser un coefficient γ compris entre 1 et 2.
Tableau 2
Perte maximale acceptable par euro collecté auprès de la classe supérieure (deux fois plus riche) en fonction du coefficient g
Dans l’approche rawlsienne, l’aversion aux inégalités peut s’interpréter comme de l’aversion au risque. Supposons que dans les limbes, vous deviez jouer à pile ou face pour déterminer la classe sociale à laquelle vous appartiendrez votre vie durant. Dans ce cas, la question de la redistribution soulevée ci-dessus peut s’interpréter comme une demande d’assurance pour réduire le risque auquel vous êtes confronté sous ce voile d’ignorance et l’aversion aux inégalités est en fait une aversion au risque.
L’estimation du coefficient γ a fait couler beaucoup d’encre dans la profession et le débat n’est pas terminé. Dans un contexte intertemporel, Stern (1977) obtint une estimation de γ autour de 2, dans un intervalle assez large compris entre 0 et 10[10]. Hall (1988) propose γ = 10, tandis qu’Epstein et Zin (1991) trouvent une valeur comprise entre 1,25 et 5. Pearce et Ulph (1995) estiment plutôt leur γ entre 0,7 et 1,5. Dans la suite, j’utiliserai une valeur de γ de 2.
Le taux d’actualisation est croissant à la fois par rapport au degré γ d’aversion aux inégalités et au taux de croissance de l’économie. La règle de Ramsey (1928) donne une formule explicite de ce lien. Elle montre que le taux d’actualisation est égal au produit de γ par le taux de croissance réelle de PIB par habitant[11]. Comme je propose de considérer γ = 2, le taux d’actualisation doit être égal au double du taux de croissance économique, selon la formule de Ramsey. Dans le tableau 3, j’ai estimé le taux de croissance économique de différents pays sur la base de sa moyenne observée sur la période 1969-2010. Dans les pays développés, le taux de croissance réel du PIB par habitant a été compris autour de 2 %, impliquant un taux d’actualisation autour de 4 %. Dans les pays émergents en revanche, la croissance a été par définition beaucoup plus forte, impliquant un taux d’actualisation beaucoup plus important, au-delà de 15 % par exemple pour la Chine. Finalement, certains pays africains ont affronté une croissance négative, impliquant un effet richesse et un taux d’actualisation négatif. On peut néanmoins espérer que le cauchemar économique de l’Afrique subsaharienne postcoloniale prenne un jour fin, cette anticipation impliquant un taux d’actualisation plus élevé que celui décrit dans cette table.
Tableau 3
Effet richesse et taux d’actualisation estimés à
partir du taux de croissance moyen du PIB réel par habitant sur la période 1969-2010
avec  = 2
= 2
Cette calibration suppose héroïquement que le taux de croissance du passé est extrapolable sur l’avenir. Dans la réalité, la croissance économique est à la fois cyclique et incertaine. Si les anticipations de croissance sont cycliques, il est indispensable que le taux d’actualisation le soit aussi. Il faut donc se préparer à organiser une révision périodique du taux d’actualisation. Comme les taux d’intérêt sur les marchés, il doit croître dans les périodes d’accélération économique et décroître en période de ralentissement. Cela correspond d’ailleurs à ce que les ménages font en fonction de l’anticipation de l’évolution de leurs revenus : ils réduisent leur épargne en cas d’anticipations plus optimistes et ils l’augmentent lorsque ces anticipations se retournent. Les variations du taux d’actualisation le long du cycle des affaires décentralisent ces variations des efforts pour l’avenir.
5. L’effet précaution et la règle de ramsey étendue
Il n’y a pas beaucoup de sens à fonder un principe de valorisation et de décision tenant compte des générations futures sur une hypothèse de croissance certaine sans fin. La croissance est un phénomène volatile par nature. De tout temps, nos sociétés ont été confrontées à des chocs, parfois très violents et durables, qui ont profondément affecté leur histoire. La Chine, région la plus développée du monde au XVe siècle, s’est retrouvée parmi les plus pauvres durant les deux derniers siècles jusqu’à son extraordinaire come-back actuel. L’Occident a connu la prospérité puis l’effondrement de l’empire romain, suivi pour l’essentiel d’un long sommeil avant la révolution industrielle. Selon Clark (2007), le salaire journalier en Babylone au milieu du deuxième millénaire avant Jésus-Christ était de 15 livres de blé. Durant l’âge d’or de la Grèce antique sous Périclès, il était de 26 livres. En Angleterre autour de 1780, il n’était plus que de 13 livres de blé. Le choc de la révolution industrielle et l’abandon de la loi de Malthus a remplacé une tendance de croissance quasi nulle sur plusieurs millénaires par une tendance de croissance de 2 % par an. Qui peut dire s’il s’agit d’une aberration temporaire de l’Histoire ou d’une altération définitive du destin de l’humanité sur terre? Les tenants d’un déclin inéluctable évoquent la disparition des ressources non renouvelables (notamment les énergies fossiles), la fin des découvertes scientifiques, les crises sanitaires majeures, etc. Les optimistes soutiennent l’idée d’un développement soutenu de façon permanente par la conquête spatiale ou les innovations technologiques et scientifiques, en particulier dans les secteurs des énergies vertes, des technologies de l’information, des biotechnologies et de la génétique.
Quoiqu’il en soit, justifier par la certitude d’un avenir radieux l’éclipse des considérations du futur lointain dans les décisions présentes avec un taux d’actualisation de 4 % n’est pas acceptable. Tout principe de décision relatif au développement doit tenir compte des incertitudes considérables qui entourent notre avenir collectif. La calibration de l’effet richesse avec une croissance du PIB par habitant espérée ne suffit pas. Il faut tenir compte d’un effet de précaution. Pour éclairer un principe de décision collective, on devrait s’inspirer de l’observation des comportements individuels. Or, on sait bien que les ménages augmentent leur épargne de précaution lorsque l’incertitude sur l’évolution de leurs revenus s’accroît. En un mot, l’incertitude sur l’avenir incite les ménages à accumuler plus de richesse de manière à leur permettre de mieux l’affronter. Cette hypothèse émise d’abord par Keynes a été systématiquement vérifiée depuis par les études économétriques (voir par exemple Guiso, Jappelli et Terlizzese, 1996). Depuis Leland (1968), Drèze et Modigliani (1972) et Kimball (1990), nous savons que cette hypothèse comportementale de prudence est vérifiée si et seulement si l’utilité marginale est une fonction convexe de la consommation. En effet, si l’utilité marginale est convexe, introduire un risque d’espérance nulle sur la consommation future augmente l’espérance d’utilité marginale et donc l’intérêt d’investir aujourd’hui pour augmenter cette consommation future. Plus cette fonction est convexe ou plus l’incertitude est importante, plus cet effet de prudence est important et plus il est désirable d’augmenter les sacrifices présents pour affronter l’avenir incertain. Dans une économie décentralisée, ceci est atteint en réduisant le taux d’actualisation.
Donc, si l’aversion aux inégalités qui justifie l’effet richesse dépend de la décroissance de l’utilité marginale, l’effet précaution dépend lui de la convexité de cette utilité marginale. Eeckhoudt et Schlesinger (2006) proposent un test simple pour déterminer si nos préférences respectent cette hypothèse de prudence. Considérons deux maux : une perte certaine de 100 euros d’une part et une loterie d’espérance nulle (par exemple un risque de gagner ou perdre 50 euros avec égales probabilités) d’autre part. Imaginons maintenant que je vous propose de jouer à pile ou face, en vous laissant le choix entre deux jeux. Dans le jeu A, les deux maux doivent être simultanément supportés si la pièce tombe sur pile. Dans le jeu B, seule la perte de 100 est supportée si la pièce tombe sur pile et seule la loterie d’espérance nulle est supportée si la pièce tombe sur face. Eeckhoudt et Schlesinger (2006) montrent que si l’utilité marginale est convexe, alors on préfère nécessairement B à A. Plus généralement, un individu prudent est celui qui préfère systématiquement répartir deux maux dans des états du monde équiprobables différents que de les concentrer dans un même état. Je considère que c’est un argument fort intuitif en faveur de cette hypothèse.
Pour résumer, l’effet de la précaution sur le taux d’actualisation est négatif. Cet effet est une fonction croissante de l’incertitude et du degré de prudence. Il existe une version de la formule de Ramsey étendue à l’incertitude. Cette formule « étendue » définit le taux d’actualisation comme la différence entre un « terme richesse » et un « terme précaution ». Comme on l’a vu tout à l’heure, le terme richesse est le produit de γ et du taux de croissance espéré de l’économie. Le terme précaution est égal à la variance de ce taux de croissance multiplié par γ(1+γ)/2. Si je maintiens l’hypothèse γ = 2, ceci signifie que l’incertitude réduit le taux d’actualisation d’un terme égal à 3 fois la variance du taux de croissance. Dans le tableau 4, pour estimer la volatilité de la croissance, j’ai repris les mêmes données que celles utilisées dans le tableau 3. Dans les pays développés, la croissance a été relativement stable autour de la tendance, ce qui donne des effets précaution très faibles par rapport à l’effet richesse décrit dans le tableau précédent, tous inférieurs à un quart de pourcent. Pour d’autres pays, les instabilités semblent plus fortes, ce qui justifie de réduire le taux d’actualisation plus vigoureusement pour tenir compte de l’incertitude que cette instabilité induit pour l’avenir. Le cas du Libéria est extrême puisqu’en plus d’avoir déjà un effet de richesse négatif, ce pays a un effet précaution très élevé, le tout conduisant à recommander un taux d’actualisation de -15 % à partir de cette méthode!
Tableau 4
Effet précaution et taux d’actualisation estimés à
partir de la volatilité du taux de croissance du PIB réel par habitant sur la période
1969-2010, avec  = 2
= 2
Si on reproduit cette méthode d’estimation du taux d’actualisation par l’utilisation de la formule de Ramsey étendue à l’incertitude pour les 190 pays de la base de données ERS/USDA, on obtient le tableau de fréquence du graphique 2. Le taux d’actualisation moyen est égal à 2,54 %, mais la dispersion est assez importante autour de cette moyenne, avec un écart-type de 3,93 %. Pratiquement, les deux tiers des taux d’actualisation se trouvent dans une fourchette de 0 à 6 %.
La formule de Ramsey étendue n’est exacte que sous deux hypothèses très spécifiques. La première contraint les préférences à la constance de l’aversion relative aux inégalités. Sans rentrer dans les détails, cela signifie que la réponse à la question décrite dans le tableau 2 ne dépend que du fait que la classe aisée est deux fois plus riche que l’autre, indépendamment du niveau de développement économique global. De même, cette hypothèse signifie que la réponse à la question liée au tableau 3 est indépendante de l’unité monétaire utilisée. Les économistes admettent traditionnellement cette hypothèse, bien qu’elle exclut la possibilité d’un minimum de consommation vital positif en dessous duquel la survie n’est pas possible. Dans Gollier (2002), je montre comment la formule de Ramsey étendue doit être modifiée si cette hypothèse de constance de l’aversion n’est pas respectée.
Graphique 2
Tableau de fréquence du taux d’actualisation dans 190 pays par la formule de Ramsey étendue à l’incertitude à partir de l’estimation de la tendance et de la volatilité de la croissance du PIB par habitant sur la période 1969-2010
La deuxième condition à satisfaire pour que la formule de Ramsey étendue soit exacte est que l’incertitude sur l’évolution de la consommation soit normale, au sens où elle soit distribuée selon la courbe en cloche gaussienne. Il y a néanmoins des raisons de croire que la volatilité du taux de croissance n’est pas normalement distribuée. Au contraire, les queues de distribution semblent beaucoup plus épaisses, avec une fréquence d’événements extrêmes (comme la crise des subprimes) beaucoup plus élevée que celle prédite sous l’hypothèse normale par la simple estimation de la moyenne et de l’écart-type issus des observations. Barro (2006) montre que la prise en compte de tels événements observés dans différents pays au XXe siècle permet de résoudre les paradoxes de la finance, dont le paradoxe dit du taux sans risque proposé par Weil (1989) (selon lequel le taux d’intérêt sans risque observé sur les 100 dernières années est plus faible que celui prédit par la formule de Ramsey étendue). En effet, la possibilité d’événements extrêmes plus fréquents que ceux prédits par la loi normale augmente le risque et donc l’effet précaution. Cela réduit le taux d’actualisation. Weitzman (2007) va plus loin. Il montre que le simple remplacement de l’hypothèse de normalité du risque de croissance par une hypothèse de loi de Student, pourtant aussi proche que l’on veut de la loi normale mais impliquant des queues de distribution plus épaisses, augmente infiniment l’effet précaution. Weitzman (2007) démontre que si nos croyances sont décrites par une loi de Student, alors le taux d’actualisation désirable est égal à… moins l’infini. Dans ces conditions, tout investissement marginal qui accroît la consommation future est désirable, quels que soient les sacrifices qu’il implique pour les générations présentes! Ce qu’il faut retenir de ceci, c’est la fragilité de la formule de Ramsey étendue, et l’importance de la prise en compte des événements extrêmes, qui tend à réduire le taux d’actualisation plus fortement qu’avec la formule de Ramsey étendue. C’est pourquoi je recommande d’utiliser un taux d’actualisation autour de 2,5 %–3 % pour tenir compte de cette observation, plutôt que les 3,43 % indiqués pour la France dans le tableau 4.
J’ai jusqu’à maintenant calibré le taux d’actualisation spécifique à chaque pays selon les spécificités de son processus de croissance, en le supposant pérenne au-delà de sa volatilité intrinsèque. Cet exercice est utile pour les projets sans risque dont les coûts et les bénéfices sont équitablement répartis au sein de la population du pays. Imaginons au contraire que nous devions évaluer un projet planétaire (comme la lutte contre le changement climatique) dont les flux sont symétriquement répartis par tous les habitants de la terre. Une méthode consisterait à calibrer la formule de Ramsey étendue en utilisant la tendance et la volatilité du PIB par habitant mondial. En utilisant la période d’estimation 1969–2010, on obtient un effet richesse de 2,82 % et un effet précaution de -0,06 %, et donc un taux d’actualisation de 2,76 %. Néanmoins, cette méthode est incorrecte parce qu’elle ne tient pas compte des fortes inégalités au niveau mondial et de la faiblesse des mécanismes de solidarité entre nations.
6. La structure par terme des taux d’actualisation
On peut appliquer cette formule de Ramsey étendue pour n’importe quel horizon temporel en vue de déterminer le taux auquel il faut actualiser le flux correspondant. On obtient donc une structure par terme du taux d’actualisation. Intuitivement, l’effet richesse justifie un taux d’actualisation constant si la tendance de croissance est constant, la croissance exponentielle de la consommation justifiant une décroissance exponentielle de la valeur présente d’un bénéfice futur. On peut montrer que l’effet précaution justifie aussi un taux d’actualisation constant si le taux de croissance suit une marche aléatoire. Donc, dans le cas d’un processus de croissance du PIB par habitant suivant un mouvement brownien géométrique, la structure par terme du taux d’actualisation est plate.
Pour la France, l’impact de l’incertitude sous cette hypothèse brownienne est de réduire le taux d’actualisation de 3,50 % à 3,43 %, uniformément pour toutes les maturités. La faiblesse de cet impact est intuitivement surprenante, étant donné l’importance de cet élément d’incertitude dans les débats publics touchant au développement durable. Ce paradoxe évoqué initialement par Gollier (2002) dans ce contexte est équivalent au paradoxe dit du « taux sans risque » en théorie de la finance. Avec Weitzman (2007), je défends l’idée que ce paradoxe peut être levé en tenant compte des vraies caractéristiques de nos croyances sur la croissance future de nos économies. En fait, la formule de Ramsey étendue n’est vraie que si on suppose que la croissance économique est un processus stable combinant une tendance immuable et une volatilité idiosyncratique, stable et connue. En clair, l’utilisation d’un taux d’actualisation de 3,43 % pour la France n’est satisfaisante que si on est convaincu que l’économie française croîtra pour les siècles des siècles autour d’un taux de 1,75 % par an, avec un bruit blanc normalement distribué d’écart-type 1,57 %, comme ce fut le cas durant les 40 dernières années. Je ne pense pas que ces croyances soient raisonnables. Plusieurs points peuvent être invoqués :
Se limiter aux 40 dernières années pour prédire l’avenir sur plusieurs siècles, c’est un peu court. Après tout, si on prend comme référence les 3 derniers millénaires, le taux de croissance annuel moyen a été infiniment plus faible que les 1,5–2 % qui servent de référence pour justifier une actualisation à 3–4 % par an. Je pense qu’il est raisonnable de tenir compte dans la modélisation de la croissance économique d’une possibilité d’un brusque retour à une tendance de croissance faible, symétriquement au brusque basculement dans la révolution industrielle il y a un peu plus de 2 siècles.
Le taux de croissance ne suit pas une marche aléatoire. Au contraire, il subit des chocs qui sont persistants. Une innovation technologique génère un gain de croissance qui s’étale sur de nombreuses années, souvent des décennies. Cela engendre des dynamiques stochastiques impliquant des cycles et des phénomènes de « retour à la moyenne ».
Même si le taux de croissance suit une marche aléatoire, on ne connait que très partiellement ses caractéristiques. En d’autres termes, on ne connait pas aujourd’hui les paramètres de cette marche aléatoire, même si on les apprendra au fur et à mesure de l’observation.
Je pense que ces trois points illustrent des caractéristiques de nos croyances collectives sur l’évolution de notre société. Elles satisfont toutes une propriété essentielle : par rapport au processus de référence dans lequel le taux de croissance suit une marche aléatoire, nos croyances réelles subissent des chocs qui sont persistants. Cela tend à magnifier l’incertitude de long terme, sans changer le risque de court terme. En conséquence, l’effet précaution augmente avec le temps plus vite que dans le cas de référence dans lequel nous avons vu que le taux d’actualisation est indépendant du terme. Donc, la structure par terme du taux d’actualisation sera décroissante avec de telles croyances, comme je le montre dans Gollier (2008).
Dans le graphique 3, je considère quatre processus de croissance suivants :
Dans le processus PR, considéré comme processus de référence, le taux de croissance annuel suit une marche aléatoire d’espérance µ = 1,75 % et d’écart-type σ = 1,57 %. Cela veut dire que les chocs sur le taux de croissance sont purement temporaires et que l’observation du taux de croissance de cette année ne donne aucune information sur le taux de croissance de l’an prochain.
Dans le processus PM, il y a deux états du monde. Dans le bon état, la tendance de croissance est de 1,75 %, tandis qu’elle est de 0 % dans le mauvais état. Chaque année, il y a une probabilité de 1 % de changer d’état. On rajoute une volatilité autour de la tendance qui est égale à σ = 1,57 %. Dans cette économie, on voit que le choc sur le taux de croissance est très persistent, avec de longues séquences de croissance nulle et de longues périodes de croissance élevée. On suppose qu’on est actuellement dans le bon état.
Dans le processus PAR1, le taux de croissance subit des chocs persistants avec un retour à la moyenne. Concrètement, le taux de croissance d’une année est égal à la moyenne du taux de l’année précédente et du taux historique de 1,75 %, plus un bruit blanc d’espérance nulle et d’écart-type σ = 1,57 %. Cela signifie que si le taux de croissance est actuellement au-dessus de 1,75 %, il y a de bonnes chances que cela reste vrai l’an prochain, mais que cette surperformance de l’économie s’estompera à l’avenir. Dans la calibration reproduite dans le graphique 3, on suppose que le taux de croissance de l’année initiale est de 1,75 %.
Finalement, dans le processus PIP, le processus de consommation est comme dans le cas PR une marche aléatoire, mais on est confronté à une incertitude paramétrique sur la tendance de croissance. Cette tendance est égale à 3 % ou 0,5 % avec d’égales probabilités. La volatilité est connue et égale à σ = 1,57 %.
Si la structure est plate pour le processus PR avec un taux de croissance suivant une marche purement aléatoire, les trois autres structures sont bien décroissantes. Dans le cas du processus PAR1 avec retour à la moyenne, la décroissance du taux se limite à un horizon temporel très court, car la persistance des chocs est très faible. Dans les processus PM de Markov et PIP avec incertitude paramétrique, la persistance des chocs est importante et de longue durée, ce qui implique une amplitude de la décroissance plus importante et plus longue. Dans ces deux cas, l’incertitude et l’effet précaution sont des éléments clé de la détermination du taux d’actualisation.
Graphique 3
Structure par terme des taux d’actualisation de 1 à
250 ans pour 4 processus de croissance économique, avec  = 2
= 2
7. Cohérence temporelle
Depuis les travaux de Strotz (1956) et Phelps et Pollack (1968), on sait que l’utilisation d’un taux de préférence pure pour le présent qui dépend de l’horizon temporel conduit à un comportement qui est intertemporellement incohérent. Dans un monde sans incertitude, cela signifie que l’action en t + 1 qui maximise le bien-être intertemporel du décideur en t n’est plus optimale lorsqu’arrive t + 1. Comme la meilleure action en t dépend en général de ce qu’on fera en t + 1, toute planification rationnelle est vouée à l’échec dans une telle situation. Le même constat peut être fait en situation d’incertitude si on se rappelle qu’une stratégie dynamiquement optimale est définie de façon contingente aux états du monde. Il est évidemment indispensable que l’action publique soit dynamiquement cohérente. Est-ce que le processus d’évaluation de l’action publique défini dans cet article conduit à des décisions intertemporellement cohérentes? Certains économistes ont mis en doute que la réponse à cette question soit positive, en observant que le taux d’actualisation dépend en général de l’horizon temporel. En produisant cet argument, ces économistes confondent le taux d’actualisation monétaire avec le taux de préférence pour le présent. Comme je propose dans cet article de considérer un taux de préférence pour le présent nul pour tous les horizons et à tout moment, le processus de décision induit par cette méthode d’évaluation est dynamiquement cohérent.
Je vais illustrer ce résultat par un exemple assez simple qui permettra par ailleurs au lecteur de réviser ses connaissances. Considérons une économie dans laquelle le taux de croissance sera certainement de 2 % dans les 12 prochains mois. Par contre, il y a beaucoup d’incertitude sur le taux de croissance l’année suivante. À la date d’aujourd’hui, nos croyances sur ce taux sont normalement distribuées avec une espérance de 2 % et un écart-type très élevé de 16,33 %. Cette incertitude sera levée dans 12 mois. On suppose que le taux de préférence pour le présent est nul, et que le coefficient γ est égal à 2. On obtient immédiatement par la formule de Ramsey que le taux d’actualisation à 1 an est aujourd’hui égal à 4 %. Un rapide calcul montre que le taux à utiliser aujourd’hui pour un bénéfice certain dans 24 mois est de 0 %[12]. L’incertitude de la deuxième année justifie de prendre un taux d’actualisation nul pour les bénéfices se réalisant à 24 mois. Supposons que nous ayons à choisir entre deux projets mutuellement exclusifs aujourd’hui. Le premier projet garantit un bénéfice certain de 1€ dans deux ans. Le second garantit un bénéfice certain de 1,04 € dans un an. Vu d’aujourd’hui, les deux projets ont des valeurs actuelles exactement identiques et le décideur devrait être indifférent.
Projetons-nous maintenant à 12 mois moins un jour, alors que l’incertitude sur la croissance économique de la seconde année n’est pas encore levée. La cohérence dynamique requiert que le simple passage du temps sans aucune nouvelle information ne modifie pas l’indifférence entre les deux projets telle qu’évaluée 12 moins plus tôt. À la fin de la première année, le second projet garantit le versement de 1,04 € immédiatement. Le premier projet garantit 1€ dans 12 mois. En utilisant la règle de Ramsey étendue, on sait que le taux d’actualisation à utiliser dans 1 an (moins un jour) pour actualiser un bénéfice dans 2 ans est égal à 2 × 2 % – 3 × 0,16332 = –4 %. La valeur actuelle de cet euro dans un an est donc de 1,04 €. A nouveau, les deux projets ont la même valeur, et l’indifférence est maintenue. Plus généralement, le simple passage du temps dans ce modèle ne pourra jamais modifier l’ordre de préférence des projets.
8. Actualisation de projets risqués
J’ai alerté à plusieurs reprises le lecteur sur le fait que le taux d’actualisation qui fait l’objet de cet article est celui qu’il faut utiliser pour actualiser un coût ou un bénéfice certain. Néanmoins, la plupart des projets d’investissement engendrent des flux dont l’impact est incertain. Dans cette section, je discute la manière dont il faut prendre en compte le risque dans l’évaluation des investissements. Cette section reprend certaines des idées développées dans le Gollier (2011) commandé par le ministre de l’Écologie au Centre d’analyse stratégique (CAS).
Si les parties prenantes à un projet d’investissement étaient neutres vis-à-vis du risque, il suffirait de calculer la valeur actuelle nette du flux espéré pour en déterminer la valeur socioéconomique. Le fait qu’ils éprouvent de l’aversion pour le risque justifie que l’on corrige ce flux espéré par une prime de risque. Le flux dit « équivalent certain » (EC) tient compte des caractéristiques de risque du flux et de l’aversion pour le risque des bénéficiaires de ce flux. Il est défini par la propriété que le bénéficiaire de ce flux est indifférent entre être confronté à ce flux incertain et recevoir avec certitude cette somme EC, les deux à la date d’échéance considérée. Techniquement, les espérances d’utilité des deux options doivent être identiques. On définit la prime de risque comme la différence entre le bénéfice espéré et son EC. C’est donc le coût du risque. Après avoir calculé l’EC des bénéfices nets à chaque échéance, il ne reste plus alors qu’à évaluer ce flux équivalent certain. Comme expliqué plus haut, cette évaluation est obtenue par la VAN de ce flux d’EC en utilisant le taux d’actualisation des projets sans risques.
Cette approche est opérationnellement complexe. Elle nécessite d’estimer pour chaque échéance la distribution de probabilités des bénéfices nets et leur relation statistique avec le reste de l’économie. Le cas le plus simple se produit lorsque le bénéfice net socioéconomique est incertain, mais statistiquement indépendant des autres risques dans l’économie. Supposons pour commencer que ce risque soit porté par un seul agent économique. Dans ce cas, l’aversion pour le risque de cet agent implique que la prime de risque soit positive, c’est-à-dire que l’EC soit inférieur au bénéfice espéré. Ce coût du risque est approximativement proportionnel à l’aversion au risque mesuré par le coefficient γ et à l’intensité du risque mesuré par la variance du bénéfice net. Ceci signifie que le coût du risque porté par un individu est proportionnel au carré de la taille du risque qu’il porte.
Ce dernier point est important. En effet, supposons qu’on puisse partager équitablement le risque entre deux individus plutôt que de le faire supporter par un seul. En partageant le risque en deux, on divise par quatre la variance du risque supporté par chacun et donc aussi son coût individuel. Du point de vue collectif, après l’addition des coûts du risque individuels, on a divisé par deux le coût collectif du risque. Plus généralement, en impliquant n personnes dans le portage du risque du projet, on divise par n le coût collectif du risque. C’est le bénéfice de la mutualisation des risques. Demander à 1 000 personnes de porter chacun un millième d’un risque donné, c’est beaucoup mieux que de demander à une seule personne de porter l’intégralité de ce risque. À la limite, pour de très grands n, le coût du risque tend vers zéro. Bien que les ménages soient risquophobes, l’évaluation des risques diversifiables devrait se faire comme s’ils étaient neutres face au risque. Ce résultat, souvent désigné comme le théorème de Arrow et Lind (1970), s’explique par le fait que nous sommes tous approximativement neutres face aux petits risques. Pour expliquer ce point, permettez-moi de revenir à la question dont le tableau 3 donne les réponses possibles. Vous devez jouer à pile ou face vos revenus annuels pour le reste de votre vie. Dans le jeu initial, vos revenus étaient de 80 000 € ou 120 000 € avec d’égales probabilités. Dans le nouveau jeu, vos revenus seront de 100 000 € ± 1 €. Je pense que la plupart d’entre nous ne seraient pas prêts à donner même un dixième de centime pour éliminer ce risque.
On ne peut donc pas séparer le problème de la prise en compte du risque dans l’évaluation d’un investissement de la manière dont le risque est alloué dans la société. Comme la mutualisation des risques crée de la valeur, comme je viens de le montrer, il n’est pas surprenant qu’il existe dans nos économies de nombreux mécanismes relativement efficaces de mutualisation. L’assurance (privée et publique) en est l’exemple le plus évident. Les marchés financiers jouent aussi un rôle crucial, en offrant aux entrepreneurs la possibilité de partager le risque d’entreprendre avec des actionnaires potentiellement très nombreux et disséminés sur l’ensemble de la planète. Le financement des investissements publics par le contribuable offre aussi la garantie d’une bonne mutualisation des risques au niveau d’un pays. Par exemple, un projet public impliquant une incertitude sur les coûts de l’ordre de ± 600 millions d’euros n’implique qu’un risque de ± 10 euros pour chacun de nos 60 millions de concitoyens.
Il faut néanmoins mettre un bémol à ce tableau. Beaucoup de risques théoriquement mutualisables restent en pratique concentrés dans les mains d’un nombre réduits d’acteurs. Les raisons en sont maintenant bien connues. Les transferts de risque créent du risque moral[13] et de l’antisélection[14] qui, au mieux, augmentent les coûts de transaction (évaluation, sélection, signalement, monitoring, audit…) et au pire, rendent les risques inassurables. Par exemple, les risques liés au capital humain (chômage, santé …) ne sont que très partiellement assurables. Dans les partenariats public/privé, les risques d’entreprendre doivent rester assez largement entre les mains de l’opérateur de manière à lui offrir suffisamment d’incitation à mener à bonne fin l’opération. La crise des subprimes a par ailleurs bien montré que les marchés disséminent les risques avec une déperdition considérable de l’information et des incitations. Dans ce contexte de second rang très détérioré, le théorème de Arrow-Lind est souvent inapplicable et l’évaluateur devra imputer aux projets dont les risques sont les moins mutualisables une prime qui tient compte de l’exposition au risque des parties prenantes les plus vulnérables. Cette règle de valorisation aura l’avantage supplémentaire d’inciter les acteurs supportant le projet à réfléchir à des mécanismes efficaces de mutualisation des risques que ce projet engendre. Par exemple, si on considère l’installation d’infrastructures pour l’exploitation de gaz de schiste, il est important de tenir compte des incertitudes sur les impacts sanitaires et environnementaux subis essentiellement par la population locale. Cela incitera les promoteurs de ces investissements à une meilleure prévention, ainsi qu’à un renforcement des garanties de responsabilité, d’assurance et d’indemnisation des dommages potentiels.
Les risques indépendants des autres risques dans l’économie ont la caractéristique désirable d’être totalement diversifiables par mutualisation, au moins en théorie. Toutefois, très souvent, les bénéfices nets anticipés des investissements sont positivement corrélés avec l’activité économique. Une infrastructure de transport, un parc de production d’électricité et beaucoup de capitaux humains auront une valeur socioéconomique plus importante en cas de boom qu’en cas de récession. Les risques liés à ces investissements ne seront pas totalement diversifiables même si la mutualisation était parfaite. Le théorème de Arrow-Lind ne s’applique donc pas dans ce cas qui constitue la règle plutôt que l’exception.
Considérons le cas très particulier d’un projet d’investissement dont les bénéfices socioéconomiques nets ont une élasticité unitaire par rapport au PIB par habitant. Quand le PIB par habitant augmente (diminue) de 1 %, le bénéfice net du projet augmente (diminue) de 1 %. Dans ce cas, le risque du projet duplique exactement le risque macroéconomique. Supposons que le risque soit parfaitement mutualisé dans l’économie et que la distribution des richesses soit équitable[15]. Intuitivement, investir dans un tel projet augmente le risque macroéconomique porté par les ménages. Comme le coût du risque croît approximativement avec le carré de la taille du risque, le fait d’augmenter le risque macroéconomique initialement non nul a un effet de premier ordre sur ce coût. En conséquence, ce projet doit être pénalisé pour le supplément de risque qu’il implique pour la société. C’est une tradition héritée de la théorie de la finance que de pénaliser les projets dont les flux sont corrélés avec le marché en augmentant le taux auquel on actualise les flux espérés. Mais quelle doit être l’intensité de cette augmentation? La réponse à cette question s’appelle la prime du risque agrégé. Si les hypothèses proposées pour obtenir la règle de Ramsey étendue (constance du coefficient γ et marche aléatoire du taux de croissance) sont satisfaites, alors on peut montrer que cette prime de risque systémique est égale au produit de l’aversion pour le risque γ et de la variance du taux de croissance économique. En considérant comme précédemment γ = 2 et un écart-type de σ autour de 3 % (voir tableau 4), on obtient une prime de risque approximativement égale à 0,2 %. Je rappelle que les projets courts dont le risque est non corrélé au risque systématique devraient être actualisés à un taux autour de 3,5 %. En conséquence, pour évaluer un projet d’investissement dont le risque duplique le risque macroéconomique, il faudrait actualiser les flux de bénéfices socioéconomiques à un taux augmenté à 3,7 %.
La faiblesse de la prime de risque agrégée obtenue par cette méthode pose deux problèmes. Le premier problème provient du fait qu’elle ne correspond pas à ce qu’on observe sur les marchés. Dans un monde parfait, les marchés financiers devraient traiter l’ensemble des risques et des actifs de l’économie. La fluctuation de la valeur de ces actifs devrait donc dupliquer celle des revenus, donc du PIB par habitant. En théorie donc, on pourrait observer la prime de risque agrégée comme la différence de rendement moyen entre un portefeuille sans risque (disons des obligations d’État à 3 mois) et un portefeuille diversifié d’actions. En France, le taux réel des obligations à 3 mois a été de -2,9 %, alors que celui des actions (voir tableau 1) a été de 3,7 %, ce qui donne une prime de risque actions autour de 6,6 %. Les autres pays donnent des primes de risque du même ordre, toutes largement supérieures à la prime de risque agrégée de 0,2 %! Il faudrait un coefficient γ d’aversion au risque supérieur à 40 pour pouvoir atteindre une prime de risque agrégée proche de celle qui est observée par le marché. Comme on le voit au tableau 3, un tel niveau d’aversion au risque semble absurde, à défaut d’être irrationnel. Cette distance très importante entre théorie et observations s’appelle le paradoxe de la prime de risque. De nombreuses tentatives d’explication ont été proposées dans la littérature depuis la publication par Mehra et Prescott (1985) du premier article sur le sujet[16].
Le deuxième problème concerne le traitement des données pour l’évaluation du risque macroéconomique. Comme je l’ai expliqué plus haut, et dans l’esprit d’une critique de Barro (2006), il est probable que les ménages intègrent dans leurs croyances concernant la croissance future des événements extrêmes qui ne sont pas (encore) contenus dans les données macroéconomiques. Supposons par exemple qu’en plus d’une volatilité de 3 %, il existe un risque extrême d’une chute de 40 % du PIB par habitant. Supposons en outre que les ménages pensent que la probabilité d’un tel événement soit de 2 % par an. Alors, avec une aversion au risque γ = 2, la prime de risque agrégée monte jusqu’à 2,3 %. Ceci peut permettre d’expliquer une partie du paradoxe de la prime de risque. Confronté à ces différents résultats, la commission du CAS que j’ai présidée a décidé de retenir une prime de risque agrégée de 3 %[17].
Cette prime de risque est l’augmentation du taux d’actualisation pour les projets dont l’élasticité des bénéfices socioéconomiques avec le PIB par habitant est unitaire[18]. Comme dans la théorie de l’évaluation des actifs financiers basée sur la consommation (consumption-based CAPM), définissons le bêta d’un actif comme l’augmentation espérée en pourcentage des bénéfices nets socioéconomiques (par habitant) consécutive à une augmentation du PIB par habitant de 1 %. On peut montrer que l’augmentation du taux d’actualisation nécessaire pour compenser l’accroissement du risque systématique induit par un projet est égale au produit du bêta du projet par la prime de risque agrégée (3 %). Un bêta élevé caractérise un projet qui augmente beaucoup le risque macroéconomique porté par les ménages et donc la pénalisation qu’il faut lui imputer pour compenser ce risque supplémentaire. Au contraire, il existe des investissements dont les bénéfices nets sont négativement corrélés au PIB par habitant. Investir dans ces projets au bêta négatif est particulièrement désirable, puisqu’ils jouent un effet d’amortisseur (ou d’assurance) des chocs macroéconomiques. Les bénéfices nets de ces projets devront être actualisés à un taux plus faible que le taux sans risque.
Le bêta d’un projet d’investissement constitue donc un élément essentiel dans son évaluation. Si nous voulons en faire plus pour les générations futures, autant que ce soit dans des projets qui n’accroissent pas les risques qu’ils devront subir. L’estimation des bêtas peut être assez difficile, en particulier en l’absence de données. Déjà, l’estimation du bénéfice socioéconomique net dans un état du monde particulier est délicat, puisqu’il nécessite de calculer non seulement les coûts et les bénéfices directs, mais aussi les externalités négatives et positives générés. Le calcul de son élasticité aux variations du PIB par habitant constitue un niveau supplémentaire de complexité. Comme contribution au rapport du CAS évoqué plus haut, Pierre Fery a estimé le bêta socioéconomique de plusieurs secteurs économiques. Ce bêta est mesuré par l’élasticité de la valeur ajoutée (qui tient lieu de mesure de la valeur socioéconomique ici) aux variations du PIB par habitant sur la période 1990–2009. Certains de ces chiffres sont reportés au tableau 5. Par exemple, le bêta socioéconomique du secteur du transport est égal à 1,6. Cela signifie qu’en moyenne, le taux d’actualisation à utiliser dans le secteur du transport est égal à 3,5 % + 1,6 * 3 % = 8,3 %. Le secteur est fortement pénalisé par la forte sensibilité de sa valeur ajoutée à l’activité économique générale. Au contraire, le taux d’actualisation moyen dans le secteur des activités agricoles et énergétiques est de 6,05 %.
Tableau 5
Estimation du bêta socioéconomique sur la base de données françaises (valeur ajoutée sectorielle 1990 – 2006)
Cette méthode d’évaluation des investissements s’apparente à celle qu’utilisent les investisseurs et les financiers. Ces derniers ont l’habitude d’identifier leur taux d’actualisation par le coût moyen de leur capital, ou dans le vocable anglophone plus connu, de leur weighted-average cost of capital (WACC). Néanmoins, ce WACC est dérive d’un bêta purement financier, car il ne s’intéresse qu’à la sensibilité de la valeur de marché de l’entreprise aux variations de la rentabilité du portefeuille de marché. Du point de vue de l’actionnaire, cette approche est logique. Néanmoins, elle ne tient pas compte des externalités extrafinancières engendrées par l’activité économique de l’entreprise[19]. Parce que la volatilité des marchés financiers est beaucoup plus importante que celle du PIB par habitant, la prime de risque financière est aussi plus importante que la prime de risque agrégée. Le WACC utilisé par le secteur privé pour actualiser les flux futurs est donc souvent plus élevé que le taux d’actualisation socioéconomique recommandé dans mon rapport. Ce constat, qui peut poser de sérieux problèmes dans l’élaboration de partenariats public-privé, n’est que la conséquence des multiples inefficacités des marchés financiers évoquées plus haut.
Dans ce contexte, chaque projet a son propre bêta et donc son propre taux d’actualisation. Comme le rappellent Krüger, Landier et Thesmar (2011), un même secteur économique ne constitue qu’un portefeuille d’investissements de nature très différente, impliquant des risques ayant des bêtas très hétérogènes. Le bêta sectoriel ne constitue qu’une moyenne des bêtas des investissements du secteur. Ainsi, il ne faudrait pas que le secteur énergétique français utilise systématiquement un bêta de 0,85 pour évaluer des projets aussi divers que dans l’éolien, le nucléaire, l’hydraulique ou le photovoltaïque. Faire cela reviendrait à faire profiter de la présence de projets à faible bêta dans le secteur pour financer des projets à bêta élevés. Cela conduirait à une allocation inefficace du capital dans l’économie.
L’évaluateur est donc confronté à un défi important pour calculer le bêta spécifique du projet qu’il évalue. Prenons un exemple pour lequel l’ambigüité reste importante. Quel est le bêta d’un investissement dont l’unique bénéfice serait la réduction des émissions de CO2 et des dommages ainsi évités? Dans la plupart des modèles intégrés (DICE, PAGE…), les dommages sont proportionnels au PIB par habitant. Un effort de réduction des émissions aura donc des bénéfices plus importants en cas d’expansion qu’en cas de récession. Le bêta de ce type d’investissement devrait donc être proche de 1 dans ce type de modèle. Néanmoins, j’entends parfois l’argument selon lequel la lutte contre le changement climatique aura le bénéfice le plus important en cas d’événement extrême, avec une régression importante de notre civilisation. Cet argument ne tient pas. La simple existence d’un bénéfice dans ce scénario catastrophe ne suffit pas; il existe certainement beaucoup d’autres actions au bêta plus faible (voire négatif) qui constituent de meilleures assurances contre ce type d’événement.
Je reconnais que la prise en compte du risque dans l’évaluation des investissements reste complexe et non consensuelle. Certains économistes recommandent que cette prise en compte se fasse uniquement à travers l’adaptation des bénéfices socioéconomiques exprimés en termes d’équivalent-certain. Cette solution que j’ai présentée dans la première partie de cette section a l’avantage de garder le principe de l’unicité du taux d’actualisation, dont la vocation d’origine est de donner une valeur au report d’une consommation certaine. Néanmoins, dans le cas où la dynamique du PIB par habitant et du bénéfice socioéconomique du projet est gouvernée par une marche aléatoire dans les deux dimensions, le rapport du flux espéré et de l’équivalent certain du flux évolue exponentiellement avec le temps. Dans ce cas, la correction du flux espéré par son équivalent certain revient exactement au même que d’augmenter le taux d’actualisation d’une prime de risque fixe. Mais cette hypothèse d’évolution brownienne est évidemment rarement vérifiée. Par exemple, dans le cas d’une centrale nucléaire, les incertitudes sur les bénéfices socioéconomiques nets sont de nature très différente selon le stage du cycle de vie de cette centrale : construction, production, démantèlement et stockage des déchets ultimes. À chaque étape, son bêta. De plus, la méthode du bêta ne tient pas compte de l’existence de risques mal mutualisés dans l’économie, un phénomène qui nécessite une prise en compte spécifique au numérateur de la VAN.
Conclusion
En faisons-nous assez pour les générations futures? Cette question prend une intensité particulière alors que la crise n’en finit pas de nous inquiéter à propos du présent immédiat. Elle menace le financement parfois très important de nombreux pays riches en faveur du développement des énergies vertes, mais aussi de l’éducation et de la R&D, par exemple. Les services de ces États ont depuis plusieurs décennies pris la bonne habitude d’évaluer les investissements publics en utilisant le critère de la VAN, dont j’ai rappelé qu’il est fondé sur la recherche de l’optimum social. Il serait bon que les autres agents économiques en fassent autant. Encore faut-il que le taux d’actualisation utilisé soit compatible avec nos anticipations collectives relatives à notre avenir. J’ai montré que si nous croyons à la pérennité du taux de croissance économique autour de 1,75 % dans les années à venir, il est raisonnable d’utiliser un taux autour de 2,5 %–3,5 % pour actualiser les projets sans risque sur les horizons temporels correspondants. J’ai aussi montré qu’il existe des arguments forts pour utiliser un taux d’actualisation plus faible – jusqu’à 1 % – pour des horizons beaucoup plus lointains, compte tenu de l’importance des incertitudes qui entourent l’environnement économique de ces générations éloignées. Sans que ce soit le but recherché, cette recommandation devrait contribuer à réconcilier les penseurs du développement durable avec la science économique, sa méthode et ses outils.
Appendices
Remerciements
Les recherches conduisant aux résultats présentés dans ce document ont été financées par les Chaires « Finance durable et investissement responsable » et « Risques de marché et création de valeur » à TSE.
Notes
-
[1]
Soit r le taux de rendement sans risque dans l’économie. Considérons un projet qui coûte un euro aujourd’hui et rapporte B euros dans un an. Sa valeur actuelle nette est donc -1+B/(1+r), où le bénéfice futur a été actualisé au taux r. Si elle est positive, cela signifie que l’investissement dans ce projet combiné à un désinvestissement de un euro dans le reste de l’économie augmente le cash flow net futur B-(1+r) > 0, sans avoir d’effet aujourd’hui.
-
[2]
En fait, Nordhaus n’utilise pas l’ACB en tant que telle, mais plutôt son corpus théorique sous-jacent, la théorie utilitariste du bien-être en économie publique. Le taux de 1,4 % est compatible avec les hypothèses de Stern, dans le cadre de l’utilisation de la formule de Ramsey (voir plus loin).
-
[3]
On notera que cet argument est biaisé par le fait que ce taux contient une prime de risque. Il ne s’agit donc pas du taux d’actualisation sans risque, qui est l’objet de cet article.
-
[4]
Néanmoins, si on utilise les données pour l’ensemble des 110 dernières années, ce taux de rendement réel sans risque est de seulement 1 % aux États-Unis. Voir plus loin.
-
[5]
Voir par exemple Babusiaux (2005).
-
[6]
Parmi les défauts de l’approche du « maxmin » rawlsien, il faut noter que cet objectif conduit à ne donner aucune valeur à l’avenir dès lors que l’économie croît, même faiblement.
-
[7]
Je fais ici l’hypothèse irréaliste que les consommateurs sont patients, et que s’ils ont l’opportunité d’accroître pendant un jour leur utilité d’une unité au jour de leur choix, ils sont indifférents quant au choix de ce jour. Sur l’impatience des consommateurs, voir Frederick, Loewenstein and O’Donoghue (2002).
-
[8]
On peut par exemple penser aux inefficacités dues à la réduction des incitations au travail que la fiscalité implique.
-
[9]
La relation est la suivante : perte maximum =1- 2-γ.
-
[10]
Une interprétation possible de cette diversité des estimations est qu’il existe une forte hétérogénéité des préférences dans la population. Gollier et Zeckhauser (2005) analysent la méthode d’agrégation des préférences dans ce contexte intertemporel.
-
[11]
Cette règle de Ramsey est applicable pour les taux d’actualisation correspondant aux différentes maturités. Le taux d’actualisation annualisé correspondant à une maturité t est égal à γ fois le taux annualisé de croissance du PIB/hbt sur la période [0, t].
-
[12]
La situation à deux ans est équivalente à celle qui prévaudrait à un an avec un taux de croissance espéré de 4 % et une volatilité de 16,3 %. Les termes richesse et précaution sont donc respectivement égaux à 8 % et 3 × 0,16332 = 8 %.
-
[13]
Un risque moral se produit lorsqu’un agent détermine son action face à un risque sans en porter l’ensemble des conséquences. Si les autres parties prenantes sont incapables d’observer cette action, ce transfert du risque réduit les incitations à agir dans l’intérêt général.
-
[14]
L’antisélection se produit lorsqu’un assureur est incapable d’observer le degré de risque intrinsèque des différents assurés. Si la tarification est uniforme, les mauvais risques s’assureront plus. Plus généralement, hors du contexte d’assurance, l’antisélection désigne le phénomène selon lequel, lorsque les risques sont hétérogènes et inobservables, les porteurs de risque les plus importants ont une propension à transférer leur risque plus forte.
-
[15]
Gollier (2001) étudie l’impact des inégalités sur la prime de risque.
-
[16]
Kocherlakota (1996) propose une revue de cette littérature.
-
[17]
L’argument de Barro a été l’élément qui a déterminé ce choix. Néanmoins, il faut noter que cette décision n’est pas compatible avec un taux d’actualisation de 3,5 %, parce que la prise en compte d’un tel risque extrême augmente massivement le terme précaution de la règle de Ramsey étendue. Cette incohérence devra tôt ou tard être corrigée.
-
[18]
On dit de ces projets qu’ils ont un bêta unitaire.
-
[19]
Voir Gollier et Pouget (2011) pour l’analyse d’un modèle où certains investisseurs socialement responsables intégreraient ces externalités dans leur demande d’actif.
Bibliographie
- Arrow, K. J. et R. C. Lind (1970), « Uncertainty and the Evaluation of Public Investment Decision », American Economic Review, 60(3) : 364-378.
- Babusiaux, D. (2005), Décision d’investissement et création de valeur, Éditions Technip, Paris.
- Barro, R. J. (2006), « Rare Disasters and Asset Markets in the Twentieth Century », Quarterly Journal of Economics, 121(3) : 823-866.
- Baumol, W. J. (1968), « On the Social Rate of Discount », American Economic Review, 58(4) : 788-802.
- Clark, G. (2007), Farewell to Alms. A Brief Economic History of the World, Princeton University Press.
- Commissariat général au Plan (1985), « Recommandations sur les règles de calcul économique pour le 9e plan, Lettre au Premier ministre », mimeo.
- Diamond, P. (1977), « A framework for social security analysis », Journal of Public Economics, 8(3) : 275-298.
- Diamond, J. (2005), Collapse: How Societies Choose to Fail or Succeed, New York: Viking Books.
- Dimson, E., P. Marsh et M. Staunton (2002), Triumph of the Optimists: 101 Years of Global Investment Returns, Princeton University Press, Princeton.
- Drèze, J. H. et F. Modigliani (1972), « Consumption Decisions Under Uncertainty », Journal of Economic Theory, 5 : 308-335.
- Eeckhoudt, L. et H. Schlesinger (2006), « Putting Risk in its Proper Place », American Economic Review, 96(1) : 280-289.
- Epstein, L. G. et S. Zin (1991), « Substitution, Risk Aversion and the Temporal Behavior of Consumption and Asset Returns: An Empirical Framework », Journal of Political Economy, 99(2) : 263-286.
- Frederick, S., G. Loewenstein et T. O’Donoghue (2002), « Time Discounting and Time Preference: A Critical Review », Journal of Economic Literature, 40(2) : 351-401.
- Gollier, C. (2001), « Wealth Inequality and Asset Pricing », Review of Economic Studies, 68(1) : 181-203.
- Gollier, C. (2002), « Time Horizon and the Discount Rate », Journal of Economic Theory, 107(2) : 463-473.
- Gollier, C. (2008), « Discounting with Fat-tailed Economic Growth », Journal of Risk and Uncertainty, 37(2) : 171-186.
- Gollier, C. (2010), « Ecological Discounting », Journal of Economic Theory, 145(2) : 812-829.
- Gollier, C. (2011), « Le calcul du risque dans les investissements publics », Centre d’analyse stratégique, Rapports et Documents n° 36, La Documentation Française.
- Gollier, C. (2012), Pricing the Planet’s Future: The Economics of Discounting in an Uncertain World, Princeton University Press.
- Gollier, C. et R. J. Zeckhauser (2005), « Aggregation of Heterogeneous Time Preferences », Journal of Political Economy, 113 : 878-898.
- Gollier, C. et S. Pouget (2011), « The Good, the Bad, and the Ugly: A Theory of Profitable and Effective Socially Responsible Investments », mimeo, Toulouse School of Economics.
- Guesnerie, R. (2004), « Calcul économique et développement durable », Revue Économique, 55 : 363-382.
- Guiso, L. T. Jappelli et D. Terlizzese (1996), « Income Risk, Borrowing Constraints, and Portfolio Choice », American Economic Review, 86(1) : 158-172.
- Hall, R. E. (1988), « Intertemporal Substitution of Consumption », Journal of Political Economy, 96(3) : 339-357.
- Harsanyi, J. C. (1955), « Cardinal Welfare, Individualistic Ethics, and Interpersonal Comparisons of Utility », Journal of Political Economy, 63 : 309-321.
- HM Treasury (2003), « The Green Book – Appraisal and Evaluation in Central Government », London.
- IPCC (2014), Climate Change 2014: Mitigation of Climate Change, Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Edenhofer, O., R. Pichs-Madruga, Y. Sokona, E. Farahani, S. Kadner, K. Seyboth, A. Adler, I. Baum, S. Brunner, P. Eickemeier, B. Kriemann, J. Savolainen, S. Schlömer, C. von Stechow, T. Zwickel et J.C. Minx (éds), Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
- Kimball, M. S. (1990), « Precautionary Saving in the Small and in the Large », Econometrica, 58(1) : 53-73.
- Kocherlakota, N. R. (1996), « The Equity Premium: It’s Still a Puzzle », Journal of Economic Literature, 34(mars) : 42-71.
- Koopmans, T. C. (1960), « Stationary Ordinal Utility and Impatience », Econometrica, 28(2) : 287-309.
- Krüger, P., A. Landier et D. Thesmar (2011), « The WACC Fallacy : The Real Effects of Using a Unique Discount Rate », mimeo, Toulouse School of Economics.
- Krutilla, J. V. et O. Eckstein (1958), Multiple Purpose River Development, Baltimore, MD: Johns Hopkins Press.
- Laibson, D. I. (1997), « Golden Eggs and Hyperbolic Discounting », Quarterly Journal of Economics, 62(mai) : 443-479.
- Lebègue, D. (2005), « Révision du taux d’actualisation des investissements publics », Commissariat général au Plan, mimeo.
- Leland, H. E. (1968), « Saving and Uncertainty: The Precautionary Demand for Saving », Quarterly Journal of Economics, 82(3) : 465-473.
- Lomborg, B. (2004), Global Crises, Global Solutions, Cambridge University Press.
- Meadows, D. H., D. L. Meadows, J. Randers et W. W. Behrens III (1972), The Limits to Growth, A Report for the Club of Rome, Universe Books.
- Mehra, R. et E. Prescott (1985), « The Equity Premium: A Puzzle », Journal of Monetary Economics, 15(2) : 145-161.
- Nordhaus, W. D. (2008), A Question of Balance: Weighing the Options on Global Warming Policies, Yale University Press, New Haven, CT.
- Office of Management and Budget (1972), « Circular N. A-94 (Revised) to the Heads of Executive Department Establishments, Subject: Discount Rates to be Used in Evaluating Time Distributed Costs and Benefits », Washington: Executive Office of the President.
- Office of Management and Budget (2003), « Circular N. A-4 to the Heads of Executive Department Establishments, Subject: Regulatory Analysis », Washington: Executive Office of the President.
- Pearce, D. et D. Ulph (1995), « A Social Discount Rate For The United Kingdom », CSERGE Working Paper no 95-01 School of Environmental Studies University of East Anglia Norwich.
- Phelps, E. S et R.A. Pollack (1968), « On Second-best National Savings and Game-equilibrium Growth », Review of Economic Studies, 35(2) : 185-199.
- Quinet, E (2013), « L’évaluation socioéconomique des investissements publics », Commissariat général à la stratégie et à la prospective, Rapports et Documents, Paris.
- Ramsey, F. P. (1928), « A Mathematical Theory of Savings », The Economic Journal, 38(152) : 543-559.
- Samuelson, P. A. (1937), « A Note on Measurement of Utility », Review of Economic Studies, 4(2) : 155-161.
- Solow, R. M. (1956), « A Contribution to the Theory of Economic Growth », Quarterly Journal of Economics, 70(1) : 65-94
- Stern, N. (1977), « The Marginal Valuation of Income », in Artis, M. et A. Nobay (éds), Studies in Modern Economic Analysis, Blackwell: Oxford, p. 209-254.
- Stern, N. (2007), The Economics of Climate Change: The Stern Review, Cambridge University Press, Cambridge.
- Strotz R. (1956), « Myopia and Inconsistency in Dynamic Utility Maximization », Review of Economic Studies, 23(3) : 165-180.
- Weil, P. (1989), « The Equity Premium Puzzle and the Risk-Free Rate Puzzle », Journal of Monetary Economics, 24 : 401-421.
- Weitzman, M. L. (1998), « Gamma Discounting », American Economic Review, 91(1) : 260-271.
- Weitzman, M. L. (2007), « Subjective Expectations and Asset-return Puzzle », American Economic Review, 97(4) : 1102-1130.
List of figures
Graphique 1
Histogramme des estimations individuelles du taux d’actualisation dans un échantillon de 2 160 économistes du monde académique
Graphique 2
Tableau de fréquence du taux d’actualisation dans 190 pays par la formule de Ramsey étendue à l’incertitude à partir de l’estimation de la tendance et de la volatilité de la croissance du PIB par habitant sur la période 1969-2010
Graphique 3
Structure par terme des taux d’actualisation de 1 à
250 ans pour 4 processus de croissance économique, avec  = 2
= 2
List of tables
Tableau 1
Rendements réels annualisés des actifs financiers
Tableau 2
Perte maximale acceptable par euro collecté auprès de la classe supérieure (deux fois plus riche) en fonction du coefficient g
Tableau 3
Effet richesse et taux d’actualisation estimés à
partir du taux de croissance moyen du PIB réel par habitant sur la période 1969-2010
avec  = 2
= 2
Tableau 4
Effet précaution et taux d’actualisation estimés à
partir de la volatilité du taux de croissance du PIB réel par habitant sur la période
1969-2010, avec  = 2
= 2
Tableau 5
Estimation du bêta socioéconomique sur la base de données françaises (valeur ajoutée sectorielle 1990 – 2006)