Abstracts
Résumé
Les probabilités subjectives ont un rôle central dans la prise de décision. Si les modèles théoriques et les données expérimentales sont relativement silencieux en économie sur la façon dont se forment ces croyances lors du processus décisionnel, il n’est pas de même en sciences cognitives. Nous proposons ici une revue de littérature de l’étude de la métacognition au travers de modèles computationnels de détection du signal. Cette méthodologie est ensuite importée à la décision non perceptive et nous montrons comment son utilisation ouvre de nouvelles pistes de recherche dans l’étude des croyances subjectives en économie expérimentale.
Article body
Introduction
Les croyances subjectives sont au coeur de la théorie de la décision depuis l’ouvrage fondateur de Savage (1954). En effet, la plupart des modèles de décision en univers risqué ou incertain supposent que les individus attribuent un poids à chaque évènement possible à l’aide de probabilités subjectives (ou d’une transformation interne de celles-ci). Cependant rien n’est dit au sujet de la nature même de ces croyances. Cette absence d’analyse provient de la contrainte méthodologique propre à la théorie économique que sont les préférences révélées. Ainsi l’utilisation de modèles « comme si » (as if) permet d’étudier les comportements sans avoir besoin de connaissances sur leurs fondements psychologiques et biologiques. À partir de la seule observation des choix effectués, les comportements sont représentés par des fonctions de préférence. Les individus se comportent comme s’ils maximisaient leurs fonctions d’utilité. L’étude du processus de décision en lui-même est donc exclue de l’analyse. À l’inverse, les sciences cognitives se basent sur des modèles « en l’état » (as is) et étudient le véritable processus de décision qui conduit aux choix. Dans le cas des croyances subjectives, la théorie de détection du signal (TDS) fournit un modèle computationnel permettant d’étudier le processus de formation des croyances dans une tâche perceptive. Cet outil permet donc de confronter les probabilités réellement utilisées par les individus lors de leur prise de décision avec les données comportementales recueillies expérimentalement. Deux processus de décision sont analysés : comment l’individu prend une décision perceptive (décision de type I) et quel est son jugement de confiance sur la justesse de ce choix (décision de type II). Les modèles de détection du signal offrant des prédictions sur le comportement optimal, il est possible de définir des critères de qualité des probabilités subjectives observées. Cette étude de la métacognition (littéralement la cognition sur sa propre cognition, c’est-à-dire la compréhension de ses propres processus cognitifs) est un champ en pleine expansion en sciences cognitives.[1] Du point de vue de l’étude de la décision, il semble évident qu’une compréhension de la façon dont se forment les croyances subjectives permettrait de mieux comprendre et expliquer les comportements observés. Si le potentiel méthodologique est indéniable pour l’économie expérimentale, nous allons voir que l’application à des décisions non perceptives n’est pas sans poser différents problèmes et qu’il faut donc considérer l’étude de la métacognition comme une piste de recherche prometteuse plutôt qu’une solution d’analyse toute faite. Dans cet article, nous allons tout d’abord présenter les bases méthodologiques de la théorie de détection du signal pour des choix perceptifs et des jugements de confiance. Nous verrons ensuite comment la qualité métacognitive peut être mesurée par les deux principaux critères que sont la calibration et la discrimination. Dans une dernière partie, nous résumerons les résultats issus des sciences cognitives sur ce qui affecte la métacognition et nous proposerons différentes applications de l’analyse de la métacognition à des choix non perceptifs (décision de valeurs, choix de groupe et comportements assurantiels). Si la portée et l’apport potentiel de ce champ de recherche ne font aucun doute, nous verrons que son application en économie est encore loin d’être évidente et que de nombreuses étapes restent à franchir. Nous proposerons ainsi certaines pistes de recherche potentielles couvrant divers champs de l’analyse économique.
1. Théorie de la détection du signal
La théorie de détection du signal offre un cadre général d’analyse de la prise de décision en univers incertain. Son point de départ est que toute décision se prend en présence d’incertitude. Considérons le cas d’un individu qui doit décider si un évènement est survenu ou non. Il utilisera toute l’information disponible pour faire son choix mais cette information restera insuffisante ou trop bruitée pour déterminer complètement la réponse correcte. Il s’en suit la présence inévitable d’erreurs. La fréquence et la forme de ces erreurs sont liées à la nature de l’évènement et aux processus utilisés par l’individu pour former son choix. La TDS offre un cadre pour analyser de telles situations en séparant les caractéristiques des évènements et les processus de décision. Si le cadre le plus naturel pour appliquer la TDS est la décision perceptive[2], son raisonnement peut s’étendre à de nombreuses prises de décision de la vie réelle. Imaginons par exemple un médecin cherchant à déterminer la présence ou non d’une maladie pour un de ses patients. Il basera son diagnostic sur des preuves empiriques, par essence bruitées, et son jugement final sera donc fait en présence d’incertitude. Nous pouvons également prendre le cas d’un négociateur qui doit décider d’acheter ou de vendre des actions en réaction à une variation du prix dans les marchés. Il doit alors déterminer si ces fluctuations sont juste dues à des bruits ou alors si elles révèlent une vraie tendance. D’une manière générale, il s’agit pour l’individu de déterminer s’il observe un signal ou un bruit. Le signal est suffisamment faible et le bruit suffisamment fort pour que la décision soit incertaine. Il en résulte quatre situations possibles : une « détection correcte » dans le cas d’une présence du signal effectivement détectée; un « rejet correct » si la présence d’un bruit n’a pas été interprétée comme un signal; une « fausse alarme » quand le bruit a été interprété comme un signal; et enfin une « omission » quand la présence du signal n’a pas été reportée. La distribution de chaque cas dépend de la nature du signal et de la façon dont l’individu prend sa décision. Avant de présenter le cadre formel de l’analyse, notons que la TDS peut faire l’objet de trois utilisations différentes (Wickens, 2002) : un puissant outil d’analyse proposant une description précise des comportements observés; une identification des effets de traitements jouant sur les paramètres des conditions expérimentales et enfin un modèle psychologique décrivant comment l’individu prend ses décisions. Ce dernier point est évidemment sujet à débat, mais depuis l’ouvrage initial de Green et Swets (1966), la TDS a été confortée par des résultats en neurosciences montrant que le cerveau semble effectivement se comporter de façon similaire à ce qui est prévu dans la modélisation par TDS (par exemple dans le cas d’une tâche de numérosité, c’est-à-dire impliquant la capacité à discerner des quantités d’objets dans un espace donné – Piazza et al., 2004; Pica et al., 2004; Nieder et Dehaene, 2009). Cette section vise à présenter les bases de la TDS dans l’analyse des choix (TDS de type I) puis à voir comment l’étendre au cas de la confiance (TDS de type II).
1.1 Le choix ou la TDS de type I
Considérons le cas d’un individu devant déterminer si le stimulus perçu est un signal ou non. Quatre types de réponse sont possibles en fonction de la réalité {signal; bruit} et de la décision {présence; absence} :

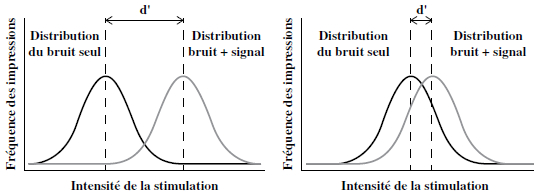
L’information sur la pertinence de la décision est réduite à deux probabilités : le taux de détections correctes (h) et le taux de fausses alarmes (f) calculées respectivement comme le nombre de détections correctes sur le nombre d’essais en présence du signal et le nombre de fausses alarmes sur le nombre d’essais en présence du bruit. Si ces probabilités permettent de nous donner une idée de la façon d’agir de l’individu, elles sont insuffisantes pour caractériser complètement la prise de décision. La TDS va plus loin et permet de mesurer la capacité de l’individu à détecter un signal, c’est-à-dire sa sensibilité. L’analyse repose sur trois hypothèses : (i) l’individu accumule de l’information sur le signal, des « évidences », qui peuvent être représentées par une valeur unique; (ii) ces évidences suivent un processus aléatoire; (iii) le choix est pris en appliquant un critère de décision basé sur la quantité d’évidences obtenues. La première hypothèse repose sur l’idée qu’il existe une réponse interne au signal qui va déterminer si l’individu pense avoir observé le signal ou non. Cette réponse codée de manière continue par une unique valeur reflète l’activité neuronale du cerveau. Cette activité est bruitée et peut être représentée graphiquement par la probabilité d’occurrence du signal en fonction de l’intensité de la réponse interne. Ainsi le graphique 1 représente la distribution du signal et du bruit lors de deux cas hypothétiques.
Graphique 1
Deux types de distributions du signal et du bruit
Note : La figure de gauche (A) présente un cas d’intensité de signal élevé et donc une décision facile avec un dʹ élevé. Dans la figure de droite (B) on observe un chevauchement du signal et du bruit et donc une décision très incertaine avec un dʹ faible.
Notons que les deux distributions peuvent différer en termes de moyennes et de variances permettant ainsi de discriminer le signal du bruit. Par ailleurs la distribution du signal est située plus à droite et implique donc des valeurs plus élevées en présence du signal. Cependant le chevauchement des deux courbes montre bien que dans certains cas, le bruit implique de plus larges valeurs et confirme donc que la justesse de la décision est incertaine. La possibilité de discriminer le signal correspond donc à la séparation et à l’écart entre les deux distributions. Si l’intensité du signal est suffisamment forte, l’écart entre les deux distributions est important et le signal est facilement distingué du bruit (graphique 1A). Dans le cas contraire, le chevauchement des deux distributions rend le signal peu discernable du bruit (graphique 1B). La différence entre le mode des deux distributions donne une mesure de la possibilité de discriminer le signal et est notée dʹ. À partir de cette information incertaine, l’individu prend une décision à l’aide d’un critère décisionnel qui coupe chacune des distributions en un point précis. Si la quantité d’évidences est supérieure à ce critère l’individu déclare le signal présent, sinon il considère faire face à un bruit.
Graphique 2
Deux types de critères décisionnels
Le placement de ce critère individuel et interne définit la stratégie décisionnelle de l’individu : un critère élevé (β2 dans le graphique 2) représente une stratégie prudente où l’individu ne reconnait la présence du signal que lorsqu’il en est pratiquement certain. À l’inverse, un critère bas (β1) conduit à une stratégie risquée dans laquelle l’individu répond positivement au moindre indice en faveur du signal. Le placement du critère implique évidemment différents taux de réponse de type détections correctes et fausses alarmes (graphique 3).
Graphique 3
Relations entre les différents types de réponse et le placement du critère décisionnel
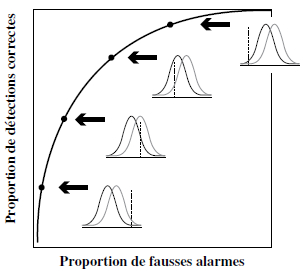
Il est alors possible de représenter pour chaque valeur de dʹ le lien entre ces deux taux en fonction du critère de décision. Ce lien est représenté sur le graphique 4 par les courbes ROC (receiver-operating characteristics). L’aire sous ces courbes nous donne alors le pourcentage d’essais correctement classés. Une aire de 0,5 correspond à des choix purement aléatoires et une aire égale à 1 indique une classification parfaite.
Graphique 4
Courbes ROC
a
b
Note : (a) Courbes ROC en fonction de différents dʹ. La partie grisée correspond au critère inférieur à 1. Ainsi les points A et B représentent des stratégies respectivement prudente et risquée pour un même dʹ de 1. (b) Courbe ROC pour un même dʹ en fonction de différents niveaux de critères.
Une dernière mesure peut être utilisée pour caractériser le comportement de l’individu : son biais, c’est-à-dire sa tendance à choisir une réponse plus souvent qu’une autre quelle que soit la distribution du signal. Ce biais se mesure comme la différence entre le critère et la moitié de la distance entre les deux distributions.
La TDS offre donc un outil puissant d’analyse de la prise de décision. En estimant la sensibilité du signal, le critère décisionnel et le biais, elle permet de définir la performance maximale d’un individu face à une tâche incertaine.[3]
1.2 La confiance ou la TDS de type II
Étant donné le succès de la TDS de type I, il est naturel d’essayer de l’appliquer à la décision de type II c’est-à-dire les jugements de confiance. Ainsi après avoir effectué son choix de type I, l’individu va estimer la confiance dans l’exactitude de cette réponse. Ce report de confiance peut s’effectuer sous de multiples formes : un simple report verbal, un choix binaire, des échelles de Likert ou un jugement de probabilités. Autrement dit, il s’agit pour l’individu de classer ses réponses de premier ordre en fonction de différents niveaux de confiance. Cette approche permet de mesurer la capacité d’un individu à discriminer entre ses bonnes et ses mauvaises réponses. En prenant par simplification une confiance binaire, les différentes réponses possibles sont les suivantes :

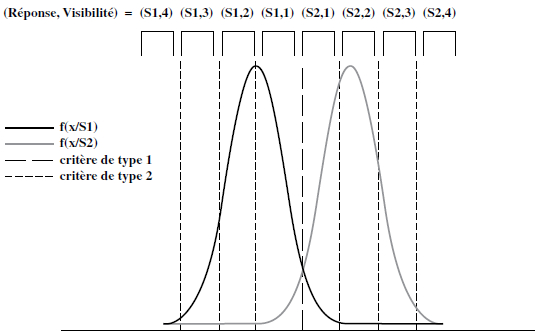
Le cadre analytique est donc similaire à celui de la décision de type I et des mesures identiques de la sensibilité de type II sont estimables. Par ailleurs, la TDS de type II fait l’hypothèse que les jugements de confiance sont basés sur les mêmes évidences utilisées pour la prise de décision de type I.[4] Le choix du niveau de confiance se fait donc en fonction des évidences reçues et des différents niveaux de critères individuels (graphique 5). L’ensemble des mesures utilisées pour la décision de type I peut ainsi être estimé pour la décision de type II.
Graphique 5
Critères décisionnels de la confiance en fonction des distributions du signal et du bruit
Note : Les mêmes évidences sont utilisées pour prendre la décision de type I et de type II. Chaque critère représente ici un niveau de confiance avec une symétrie de ces niveaux par rapport au critère de type I c’est-à-dire (S1,1) et (S2,1) correspondent à une confiance de 1 (sur une échelle de 1 à 4) respectivement pour le stimulus 1 et le stimulus 2.
À partir des taux de détections correctes et de fausses alarmes de type II, il est possible de calculer un dʹ de type II, des critères décisionnels pour chaque niveau de confiance ainsi que des courbes ROC de type II.[5] Bien qu’il soit analytiquement possible d’estimer la sensibilité de type II à l’aide du dʹ de type II ou du ROC de type II, ces deux approches présentent des lacunes les rendant plus ou moins inutilisables.
Ainsi l’approche la plus naturelle est de calculer la sensibilité de type II comme le dʹ de type II et de l’exprimer en fonction des taux de détections correctes et de fausses alarmes de type II (Kunimoto, Miller et Pashler, 2001). Ce dʹ de type II s’exprime in fine en fonction du dʹ de type I ainsi que des critères décisionnels de type I et II. Cependant calquer le cadre analytique de la TDS du choix sur celui de la confiance pose différents problèmes qui rendent cette approche peu pertinente.[6]
L’utilisation de courbes ROC de type II permet de surmonter ces problèmes en ayant recours à une approche non-paramétrique (Galvin et al., 2003; Macmillan et Creelman, 2005). Ce ROC de type II offre donc une caractérisation de la sensibilité de la confiance. Cependant son défaut majeur est sa dépendance à la sensibilité de type I et donc aux différents biais de décision.[7] Il est possible d’utiliser des techniques psychophysiques (calibration de la difficulté par des escaliers psychométriques à la Levitt, 1971) pour s’assurer que le niveau de performance est constant et identique entre sujets.[8] Cependant la difficulté à obtenir des résultats empiriques fiables joue en faveur d’une modélisation explicite du lien entre sensibilité et performance. Ainsi l’application directe de la TDS de type I à la décision de type II pose de nombreux problèmes et nous verrons dans la partie suivante comment estimer cette sensibilité de type II de manière plus efficace.
1.3 Exemple illustratif : décision perceptive en choix forcé et confiance probabiliste
En guise d’illustration des choix perceptifs de type I et II, nous présentons ici un design classique d’expérience en choix forcé avec élicitation de la confiance de manière probabiliste (graphique 6C et Massoni, 2013).
Graphique 6
Design expérimental
A
B
C
Note : (A) Exemple de stimuli perceptifs. (B) Règle d’élicitation de la confiance dite de matching probabilities. (C) Exemple d’un essai complet avec fixation, stimulus, choix de type I et de type II.
La tâche perceptive est un choix forcé entre deux alternatives (2AFC) qui est connu pour être un paradigme pertinent pour l’analyse par TDS (Bogacz et al., 2006). Lors de cette tâche, les sujets doivent comparer le nombre de points contenus dans deux cercles de diamètres identiques (graphique 6A). Les deux cercles sont présentés après un écran de fixation de manière rapide (700 ms) afin qu’il ne soit pas possible de compter le nombre de points. Les sujets doivent indiquer quel cercle contient le plus de points puis donner leur niveau de confiance dans le succès de ce choix. Nous présentons ici une confiance probabiliste où les individus doivent donner leurs probabilités d’avoir correctement répondu entre 0 et 100. Le mécanisme incitatif est la règle de matching probabilities qui incite les sujets à donner leur véritable confiance quelle que soit leur préférence vis-à-vis du risque (nous renvoyons le lecteur à la partie 3.1 pour plus d’explications).
Un avantage de ce type de stimuli est qu’il permet de calibrer la difficulté de la tâche en fonction des capacités individuelles des individus. Ainsi en utilisant un escalier psychophysique (Levitt, 1971), il est possible de déterminer de manière individuelle le nombre de points d’écarts entre les deux cercles pour obtenir une réussite moyenne de 71 % lors de l’expérience. Il convient alors de faire varier la difficulté, c’est-à-dire augmenter ou diminuer l’écart de points entre les deux cercles, lors d’une phase d’entrainement avec une variation du nombre de points après chaque échec ou après deux réussites consécutives. Le niveau de difficulté convergera alors assez rapidement (une trentaine de renversements) pour identifier l’écart de points entre les deux cercles permettant une réussite identique entre tous les sujets lors de l’expérience. Cette approche offre la possibilité de figer la réussite et donc d’étudier les croyances subjectives avec un plus grand contrôle et en disposant d’un critère objectif de performance.
Ce design expérimental permet de recueillir les choix des individus (droite ou gauche), leurs niveaux de confiance (entre 0 et 100 par pas de 5) et leur temps de réponse en fonction des stimuli présentés. La tâche s’effectuant de manière assez rapide, il est possible de faire environ 200 essais sans fatigue excessive du sujet. L’ensemble de données permet alors d’estimer les paramètres de la TDS pour le choix de type I et de type II. Ainsi, les stimuli droit et gauche (c’est-à-dire les cercles) produisent les réponses internes suivantes : ![]() et
et ![]() .
.
Comme nous connaissons les vraies valeurs x1 et xr, c’est-à-dire le nombre de points dans chaque cercle, nous pouvons estimer l’habileté à discriminer de chaque sujets, σ2i. Ensuite, le sujet doit déterminer si le signal perçu x provient de X = XL − XR positif (et donc répondre gauche) ou négatif (répondre droite). De plus, sa probabilité subjective peut être facilement déduite par une règle bayésienne (Massoni, Gajdos et Vergnaud, 2014). Il est alors possible d’estimer l’ensemble des paramètres de détection du signal du choix et de la confiance (critères décisionnels, d’, ROC que ce soit pour le type I ou le type II).
Ainsi en utilisant une tâche perceptive et la TDS, nous pouvons mesurer et estimer la façon dont un individu agit lors de son processus décisionnel. Ce qui ouvre la voie à l’étude des capacités métacognitives et l’identification de certains facteurs jouant sur la formation des probabilités subjectives.
2. Mesures de la métacognition
Au-delà de la TDS, la question se pose de savoir comment mesurer la qualité de la confiance, c’est-à-dire les capacités métacognitives d’un individu. Deux aspects sont à prendre en compte : la sensibilité de la métacognition et son biais.
Graphique 7
Dissociation entre la sensibilité métacognitive et le biais métacognitif
Note : La discrimination correspond à l’écart entre les deux distributions alors que la calibration se concentre sur le niveau moyen de confiance exprimée.
La première reflète la capacité de discrimination, c’est-à-dire la façon dont s’ajuste la confiance en fonction des performances; la seconde, la capacité de calibration, c’est-à-dire comment la confiance se rapproche de la réussite en moyenne. Nous présentons dans cette section les principales mesures utilisées.[9] Notons que si la calibration et la surconfiance sont étudiées quasi systématiquement en économie, la discrimination est quant à elle très peu analysée. Ces deux mesures captent pourtant deux aspects différents de la qualité de la confiance. Ainsi, telle qu’elle est présentée dans le graphique 7, la sensibilité dépend de l’écart entre les distributions de confiance pour les essais réussis et les essais ratés alors que la calibration ne concerne que le niveau de confiance moyen. Un exemple simple pour comprendre cette différence est le suivant (Liberman et Tversky, 1993) : un médecin prédisant le sexe d’un nouveau-né avec une probabilité de 0,5 sera parfaitement calibré (le sexe étant équiprobable) mais aura une discrimination nulle (ne pouvant discriminer entre les deux sexes possibles).
Une première mesure de performance globale de la confiance est le Brier Score (Brier, 1950). Considérons un individu qui donne sa confiance sur n évènements, pi étant sa confiance dans l’évènement Ei et xi une indicatrice valant 1 si l’évènement Ei est correctement prédit. Le Brier Score est calculé comme suit :
Comme ce score est un score d’erreur, plus il est faible plus la confiance moyenne est correcte. La décomposition de Murphy (Murphy, 1972; Yates, 1982) montre que ce score agrège un indice de calibration et un indice de discrimination. On peut en effet le décomposer comme suit :
avec ![]() le taux de succès, P l’ensemble des niveaux de confiances possibles, Np le nombre de fois où le niveau de confiance p est utilisé et fp le taux de succès au sein de ce niveau de confiance. Le premier terme, UNC, représente la variance de la variable de succès qui est indépendante de la confiance; le second terme, DI, est l’indice de discrimination mesurant la qualité du taux de détections correctes au niveau du taux global, f; le dernier terme, CI, est l’indice de calibration qui mesure la différence entre le taux observé de détections correctes (fp) et la confiance élicitée. Cette décomposition donne donc deux premières mesures de la calibration et de la discrimination.
le taux de succès, P l’ensemble des niveaux de confiances possibles, Np le nombre de fois où le niveau de confiance p est utilisé et fp le taux de succès au sein de ce niveau de confiance. Le premier terme, UNC, représente la variance de la variable de succès qui est indépendante de la confiance; le second terme, DI, est l’indice de discrimination mesurant la qualité du taux de détections correctes au niveau du taux global, f; le dernier terme, CI, est l’indice de calibration qui mesure la différence entre le taux observé de détections correctes (fp) et la confiance élicitée. Cette décomposition donne donc deux premières mesures de la calibration et de la discrimination.
En plus de cet indice de calibration, le biais est aussi caractérisé par le niveau de surconfiance. L’utilisation de cette mesure est largement répandue en économie (Camerer et Lovallo, 1999) et en psychologie (voir les revues de littérature de Lichtenstein, Fischho et Phillips, 1982; Wallsten et Budescu (1983); Harvey, 1997). Pour mesurer le niveau de calibration, la distance entre le taux de succès et la confiance moyenne est utilisée. Une mesure de la sur/sous confiance est la suivante :
Une valeur nulle reflète une parfaite calibration alors qu’une valeur négative (respectivement positive) traduit une sous-confiance (respectivement surconfiance). La sur/sous-confiance et l’indice de calibration saisissent deux aspects différents du biais : le premier mesure la tendance à un optimisme ou pessimisme excessif alors que le second étudie la différence entre confiance et taux de succès pour chaque niveau de confiance.
Si la méthode utilisée pour mesurer le biais n’est pas sujette à débat, il n’en est pas de même pour la mesure de la sensibilité. Ainsi une multitude de mesures est proposée dans la littérature (Fleming et Lau, 2014). La mesure la plus simple est l’étude des corrélations entre réussite et confiance : la ϕ-corrélation correspond à la corrélation de Pearson entre les réussites essai par essai et la confiance binarisée alors que la γ-corrélation est la corrélation de Goodman-Kruskall pour des niveaux de confiance multiples. Cette méthode fournit un premier aperçu de la sensibilité mais présente le principal défaut d’être dépendante du niveau de calibration tant pour la ϕ-corrélation (Nelson, 1984) que la γ-corrélation (Masson et Rotello, 2009). L’utilisation de la TDS permet de résoudre ce problème de dépendance de la discrimination au biais. Ainsi les mesures précédemment présentées (d’ de type II, ROC de type II) sont indépendantes du niveau de calibration. Cependant, nous avons vu que ces mesures sont elles aussi sujettes à caution. La nécessité d’une modélisation explicite du lien entre sensibilité et performance a conduit au développement d’une nouvelle mesure introduite par Maniscalco et Lau (2012, 2014), le meta-d’ et son utilisation est de plus en plus fréquente dans la littérature.[10] Le concept de meta-d’ repose sur l’idée de mesurer le signal disponible pour effectuer la tâche de type II. Ainsi le meta-d’ est le dʹ de type I qu’un observateur idéal de TDS (en termes de choix et de confiance) aurait besoin pour atteindre la sensibilité de type II observée. La comparaison entre meta-d’ et dʹ offre une mesure de la capacité à discriminer entre ses niveaux de confiance : une égalité des deux valeurs signifie que l’individu utilise toute l’information disponible lors du choix pour former sa confiance et a donc une métacognition optimale au sens de la TDS. Si le meta-d’ est inférieur, sa sensibilité de type II est sous-optimale. Le cas d’un meta-d’ supérieur peut être envisagé si l’on considère que toute l’information n’a pas été utilisée pour le choix et que de nouvelles évidences ont été accumulées entre les décisions de types I et II. Cette nouvelle mesure est clairement supérieure aux deux précédentes et les questions relatives à son estimation sont détaillées dans Maniscalco et Lau (2012, 2014) et Barett, Dienes et Seth (2013).[11] Cependant deux principaux problèmes peuvent être reliés à cette mesure : la prise en compte du biais et de la variance semblent problématiques sous certaines conditions (Barett, Dienes et Seth, 2013); de même le problème des critères décisionnels multiples en cas de niveaux de confiance non-binaire pose le problème d’une lecture multiple du meta-d’ et reste pour le moment une question ouverte. Malgré ces difficultés techniques, cette méthode offre actuellement la meilleure mesure de la sensibilité en permettant de la dissocier des aspects décisionnels de type I. Notons qu’une autre mesure propose également un indice de discrimination contrôlé pour l’effet de la performance : Yaniv, Yates et Smith (1991) proposent d’ajuster et de normaliser l’indice de discrimination du Brier Score. En normalisant par la performance et en ajustant par le nombre de niveaux de confiance utilisé, la mesure obtenue (ANDI) permet de mesurer la discrimination indépendamment de la performance.
Nous avons vu les principaux outils de mesures de la métacognition. Si les mesures de la calibration sont bien établies et peu sujettes à débat, le lien entre performance et capacité de discrimination rend l’analyse de cette dernière plus complexe. Notons cependant que les modèles de type meta-d’ et ANDI, qui prennent explicitement en compte cette relation et proposent une mesure corrigée de ce facteur, semblent les plus pertinents et les plus à même d’offrir une véritable estimation de la discrimination.
3. Principaux Résultats
Dans cette section nous présentons tout d’abord les principaux résultats permettant de caractériser la métacognition, puis nous proposerons plusieurs applications de son utilisation à des questions d’ordre économique. Notons que nous choisissons de nous concentrer essentiellement sur la capacité de discrimination plutôt que celle de calibration en raison de sa faible couverture dans la littérature économique. Le lecteur peut se référer aux différentes revues de littérature de Lichtenstein, Fischho et Phillips (1982); Wallsten et Budescu (1983) et Harvey (1997) pour une analyse détaillée de la calibration.
3.1 Capacités métacognitives
Nous cherchons ici à savoir comment se forme la qualité métacognitive et quels sont les facteurs pouvant l’influencer. D’un point de vue neuronal, les évidences sont encore récentes et non définitives. Si les études au niveau d’un unique neurone commencent à donner certains résultats, il est trop tôt pour identifier précisément ce qui a trait à la métacognition et ce qui concerne la cognition en général. Middlebrooks, Abzug et Sommer (2014) recensent les principaux travaux de cette littérature et montrent que l’activité métacognitive active des connexions neuronales chez les animaux dans les régions suivantes : le cortex orbitofrontal (OFC) chez le rat (Kepecs et al., 2008); le cortex latéral intrapariétal (LIP) chez les macaques rhésus (Kiani et Shalden, 2009) et le cortex dorsolatéral préfrontal (SEF) chez le singe. Si ces études nous donnent un point de départ, elles ne permettent pas de conclure que leurs activités sont nécessaires à la métacognition. Des études par microsimulation ou sur des patients souffrant de liaisons cérébrales précises sont nécessaires (par exemple, David et al., 2012, sur la métacognition de patients schizophréniques ou Fleming et al., 2014, sur des patients souffrant de lésions cérébrales). À défaut de pouvoir actuellement comprendre les mécanismes de formation de la métacognition, les études d’imageries montrent le rôle primordial du cortex latéral préfrontal (PFC) dans les capacités métacognitives. L’étude de Fleming et al. (2010) montre par exemple que les différences individuelles en termes de facultés de discrimination peuvent s’expliquer par la taille de la matière grise dans le PFC dorsolatéral. Nous renvoyons le lecteur à la revue de littérature de Fleming et Dolan (2012) sur les bases neuronales de la métacognition.
Si la métacognition n’est pas encore bien comprise au niveau cérébral, les facteurs l’influençant au niveau comportemental sont mieux observés. Une première question cherche à comprendre comment révéler les différents niveaux de confiance et quelle méthode d’élicitation doit être privilégiée. Overgaard et Sandberg (2012) comparent différentes méthodes de report et montrent que les reports favorisant l’introspection donnent les meilleurs résultats. Hollard, Massoni et Vergnaud (2016) et Massoni, Gajdos et Vergnaud (2014) comparent trois types de règles d’élicitation[12] : une règle libre sans incitation, une règle empruntée à l’économie expérimentale (quadratic scoring rule) avec incitation mais faisant appel à des choix de montants de rémunérations plutôt qu’à des probabilités de confiance et en enfin une règle de matching probabilities disposant à la fois d’incitations et d’une échelle en termes de pourcentage de confiance.
Deux résultats sont à retenir : les performances en termes de calibration et discrimination sont dépendantes de la nature de la règle et d’un point de vue méthodologique, seules les confiances issues du mécanisme de matching probabilities sont conformes aux hypothèses émises sur le choix de type II par la TDS. Si la façon de demander son niveau de confiance affecte la décision, il en va de même pour la nature de la tâche. Ainsi Fleming et al. (2016) étudient les décisions en termes de jugements prospectifs et rétrospectifs. Ils montrent que si la calibration est stable pour les deux tâches, il n’en est pas de même pour la discrimination. Cette étude ouvre la question de l’analyse des jugements prospectifs et en particulier les difficultés à utiliser un modèle de détection du signal sur des prédictions de choix perceptifs. Enfin les facteurs internes commencent à être étudiés et ils semblent jouer un rôle prépondérant dans le niveau de capacités métacognitives à un moment donné. Garfinkel et al. (2013) montrent que la métacognition est affectée par les processus internes et en particulier les battements cardiaques. De son côté Massoni (2014) montre que l’état émotionnel affecte la métacognition avec une amélioration à la fois de la calibration et de la discrimination dans le cas d’un sentiment d’anxiété vis-à-vis de la décision.
Globalement, l’étude des capacités métacognitives est encore un champ récent en neurosciences et en psychologie cognitive. Bien que la compréhension de ces mécanismes s’améliore au fil des expériences, il reste encore beaucoup à faire pour réellement comprendre le fonctionnement métacognitif humain.
3.2 Métacognition et décision
En raison de l’aspect récent de ce champ de recherche, peu d’études ont pour l’instant tenté d’utiliser le cadre métacognitif pour comprendre les décisions économiques. Nous allons présenter ici trois groupes d’études portant sur les décisions économiques en termes de valeurs, la décision collective et les choix assurantiels.
Une première application de la métacognition dans des décisions de nature économique peut être trouvée dans l’étude de De Martino et al. (2013). Utilisant une tâche d’évaluation (choix entre deux casse-croûtes et élicitation du consentement à payer par un mécanisme à la Becker-DeGroot-Marschak) et une tâche de révélation de la confiance, leur protocole expérimental permet de séparer le mécanisme d’évaluation des choix de celui de la formation de la confiance dans ce choix. Il est ainsi possible de dissocier les variations de la confiance des autres processus cognitifs et ainsi obtenir des mesures séparées des choix et de la confiance dans une décision de nature économique. Leurs principaux résultats montrent tout d’abord que la confiance varie bien en fonction de la variable de décision en s’adaptant à la justesse de la décision et à la valeur des différentes options. Au-delà de ce résultat comportemental, les données d’imagerie apportent des indications sur la façon dont la confiance se forme et son lien avec l’évaluation des choix possibles. Ainsi une même aire cérébrale représente la différence monétaire entre les différentes options et la confiance associée à cette comparaison des valeurs (cortex préfrontal ventro médial – vmPFC). Le report de cette confiance s’effectue au niveau du cortex préfrontal rostrolatéral (rlPFC) montrant un transfert d’information au sein du cerveau. La relation entre ce report de confiance et l’évaluation des options, c’est-à-dire la capacité métacognitive, est mise en évidence par un lien systématique entre ces deux aires cérébrales. Ainsi cette étude montre que les individus ont accès au bruit de leur prise de décision et que des changements dans le niveau de ce bruit se reflètent dans le niveau de confiance révélé. L’accès à ce bruit décisionnel permet alors d’identifier et de corriger les décisions erronées (voir également Yeung et Summerfield, 2012, pour une analyse de la prise en compte des erreurs par la confiance). L’étude de la métacognition permet ainsi de quantifier le bruit de la décision, de mieux comprendre les changements de décision et même, comme nous allons le voir, de communiquer entre individus.
Ainsi une deuxième application de la métacognition peut être trouvée dans la décision de groupe. Dans un cadre perceptif, un intérêt récent s’est porté sur la façon dont deux individus agrègent l’information disponible pour prendre une décision commune (Bahrami et al., 2010, 2012; Koriat, 2012; Sorkin, Hays et West, 2001). En particulier il a été montré que « deux têtes ne sont pas toujours meilleures qu’une ». La principale raison avancée à cette inefficience de la décision de groupe est l’hétérogénéité des performances des membres du groupe. Ainsi Bahrami et al. (2010) montrent que plus les performances des deux individus sont éloignées, plus la décision de groupe sera différente de la décision optimale. Au contraire, Massoni et Roux (2014) prouvent que ce n’est pas l’hétérogénéité des performances qui est en cause mais la différence de calibration des confiances. Leur design expérimental propose aux sujets de regarder individuellement un stimulus perceptif de discrimination visuel, de donner leur réponse ainsi que leur confiance puis de comparer avec un binôme qui aura vu le même stimulus pour trouver une décision commune à la fois sur la réponse et sur le niveau de confiance. En proposant aux individus d’échanger à la fois leur choix et leur confiance, les auteurs montrent que l’hétérogénéité de performances n’a plus d’effet sur la décision sous-optimale du groupe une fois prise en compte l’hétérogénéité en termes de calibration. Ce résultat montre bien l’importance de la capacité métacognitive dans la prise de décision commune et le partage d’information. Ce rôle de la métacognition est confirmé par une étude récente de Bang et al. (2014) montrant que l’hétérogénéité en termes de discrimination joue un rôle dans l’efficacité d’heuristiques de décision en groupe.
Nous présentons une dernière application visant à étudier dans un même cadre expérimental et analytique des décisions de type perceptif et des décisions purement économiques d’assurance vis-à vis du risque dans un cadre de confiance à la fois prospective et rétrospective. Les trois derniers chapitres de la thèse de Massoni (2013b) détaillent un protocole expérimental dans lequel les individus doivent faire des choix de loteries basés sur leur réussite à une tâche perceptive tout en ayant la possibilité de s’assurer contre cette incertitude. La capacité métacognitive est également calculée pour les décisions perceptives et pour les prédictions de succès.[13] Les résultats montrent que si les capacités métacognitives (calibration et discrimination) sont liées entre la tâche de prédiction et d’assurance ce n’est pas le cas pour la métacognition perceptive. Ce résultat insiste sur la difficulté d’appliquer un modèle général métacognitif indépendant du type de choix. La question de la prédiction est également centrale et renvoie aux résultats de Flemming et al. (2016) sur la dissociation entre discrimination de jugements prospectifs et rétrospectifs. Ainsi, si les modèles de formation de croyances, et en particulier ceux issus de la TDS, reposent sur des hypothèses réalistes pour estimer une confiance passée, ce n’est pas le cas pour les jugements prédictibles au sein desquels le signal utilisé pour former cette croyance n’est pas déterminé. L’extension de modèles de formation des jugements probabilistes à la prédiction est une étape cruciale pour l’analyse de la métacognition des décisions économiques. Si les apports de la psychologie cognitive sont certains pour la compréhension de la confiance, il convient d’appliquer et d’amender ces modèles pour permettre d’analyser le principal champ d’application des économistes qu’est la prédiction.
Malgré cette limitation, la TDS, en proposant un modèle théorique permettant de définir les décisions et les croyances optimales, offre un cadre d’analyse potentiellement fécond des comportements économiques. On peut par exemple penser à l’analyse des croyances dans un contexte assurantiel avec une mesure des distorsions en présence de risque de faibles probabilités mais aux conséquences majeures (par exemple, risques catastrophiques : risques naturels, terrorisme ou catastrophe industrielle). Une autre application se trouve dans la possibilité de faire varier les gains et coûts des 4 types de réponses possibles. Il est alors possible d’observer les déviances des comportements et des croyances par rapport aux comportements optimaux. On peut penser ici à des applications évidentes en termes de décisions médicales ou financières avec une réelle asymétrie des coûts des omissions et des fausses alarmes ainsi que des bénéfices des détections et des rejections correctes. Ces exemples sont loin d’être exhaustifs et de multiples applications sont possibles.
Ainsi, même si les prédictions sont difficiles à analyser dans un cadre de TDS, un apport immédiat à l’analyse économique réside dans la possibilité de comparer les comportements et les croyances des individus vis-à-vis des prédictions d’un modèle théorique robuste et d’analyser la façon dont des changements dans les conséquences des actions et/ou les niveaux objectifs de probabilités ont un effet sur les comportements observés. On peut donc envisager des applications multiples de ce cadre d’analyse à la compréhension des phénomènes économiques.
Conclusion
Dans cette revue de littérature nous avons présenté la manière dont la confiance peut être analysée à l’aide d’outils issus des sciences cognitives et en particulier par la TDS. En prenant en compte le fait que les travaux issus de ce champ sont encore non définitifs et que de nombreux mécanismes restent à comprendre et à modéliser, on peut tirer plusieurs conclusions de cette analyse. Tout d’abord, la TDS offre une modélisation du processus de décision utilisé par l’individu pour faire ses choix et déterminer sa confiance en ceux-ci. Face à une tâche perceptive il est possible de modéliser et d’estimer la manière d’agir d’un individu. Ces modèles computationnels offrent donc un puissant outil d’analyse et de compréhension des comportements observés. Notons cependant que nous avons ici choisi d’analyser la décision perceptive uniquement à l’aide de la TDS mais des théories alternatives existent dans la littérature. Il est ainsi possible de proposer différentes modélisations du processus de décision et nous renvoyons les lecteurs vers les trois alternatives que sont les théories de seuil (Luce, 1963b; Krantz, 1969), la théorie du choix (Luce, 1959, 1963a) et la TDS non paramétrique (Egan, 1975; Metz et Pan, 1999).
Une autre approche plus complémentaire consiste à ne plus considérer la décision comme statique mais à intégrer sa composante dynamique, c’est-à-dire les temps de réponse. L’idée principale est que l’individu accumule des évidences vis-à-vis du stimulus et doit décider quand arrêter ce processus d’accumulation pour prendre sa décision (Ratclff, 1978; Ratcliff et McKoon, 2008; Busemeyer et Townsend, 1993; Diederich, 2003). Ces modèles séquentiels de la TDS offrent un cadre d’analyse particulièrement pertinent pour les décisions sous contraintes temporelles et l’analyse de l’arbitrage temps de décision / performance. Notons que l’analyse des temps de réponse commence à devenir de plus en plus répandue en économie expérimentale.[14] Cette approche dynamique a récemment été appliquée à l’étude de la confiance avec des processus d’accumulation de type II (Ratcliff et Starns, 2009; Pleskac et Busemyer, 2010). Au-delà de leurs capacités à analyser les données expérimentales, ces modèles sont renforcés par des évidences neuronales montrant une activité de type modèle de diffusion des circuits neuronaux (Gold et Shadlen, 2007). Bien que cette approche semble particulièrement prometteuse, des difficultés computationnelles ainsi que l’absence d’évidence quant à la nature des signaux de deuxième ordre ne permettent pas actuellement de la considérer comme une modélisation définitive mais plutôt comme une piste de recherche en cours.
Si la modélisation de la TDS est particulièrement puissante pour analyser et comprendre la décision perceptive, nous avons vu que son application à des questions économiques est plus délicate. La confiance joue clairement un rôle dans la prise de décision et elle peut nous fournir un bon indicateur des erreurs de décision et donc d’explication des choix observés. De plus elle semble primordiale pour permettre aux individus de communiquer et de prendre des décisions communes. Cependant l’application directe de la métacognition aux décisions économiques est encore difficile. Savoir en quoi la capacité à discriminer d’un individu l’aide à prendre une décision économique optimale est une question ouverte. Comme nous l’avons vu, l’absence de modélisation des processus prédictibles ne permet pas actuellement d’appliquer directement la TDS aux choix de nature économiques.
Il convient cependant de nuancer cette conclusion négative en insistant sur l’aspect très récent des travaux dans ce domaine et qui doivent donc être considérés comme un processus de découverte en cours plutôt qu’un cadre d’analyse figé. L’absence d’analyse de la métacognition et en particulier de la discrimination en économie expérimentale laisse penser que son utilisation future pourrait offrir de nouvelles pistes de compréhension des comportements. En particulier l’hétérogénéité individuelle observée dans toutes les études semble jouer en faveur d’une vision de la métacognition comme d’un nouveau facteur explicatif de la décision : la métacognition servant alors à détecter ses erreurs et à corriger sa décision. Cependant, ce passage de la décision perceptive à la décision économique nécessite des avancées théoriques dans la TDS : le passage aux jugements prédictibles en est une mais aussi et surtout une modélisation de l’hétérogénéité métacognitive au sein même du modèle semble nécessaire. Ainsi l’utilisation de la TDS et l’analyse de la métacognition ne doivent pas être vues comme un outil définitif mais plutôt comme une piste de recherche en cours offrant des perspectives d’analyses nouvelles et un important potentiel d’explication du processus décisionnel.
Appendices
Annexe
Théorie de la Détection du Signal : bases des modélisations du choix de type I et II
Nous présentons ici les bases de la modélisation du choix de type I par la TDS et les prémices de la modélisation du choix de type II.
La quantité d’évidence est représentée par une variable aléatoire XS pour le signal et XN pour le bruit. Nous supposons qu’elles suivent toutes les deux une distribution gaussienne avec
Les taux de détections correctes
et de fausses alarmes,
s’expriment comme suit :
et
avec β le critère décisionnel de l’individu. En pratique le paramètre s est fixé à 1 et nous utilisons un modèle à variance égale par la suite.[15] À partir de ces deux taux nous pouvons calculer le critère, β, et le d’. Le critère est déterminé par le taux de fausses alarmes calculé sur la distribution du bruit :
Le taux de détections correctes et la distribution du signal nous donne la distance entre le critère et le d’ :
En combinant ces deux résultats nous obtenons une estimation du d’ :
Ainsi en se basant uniquement sur les comportements observés nous pouvons estimer la sensibilité des individus en fonction de la nature des stimuli. Il est également intéressant d’estimer le biais en faveur d’une réponse, c’est-à-dire la tendance à choisir plus souvent une réponse quelle que soit la distribution du signal. Ce biais se mesure comme la différence entre le critère et la moitié de la distance entre les deux distributions (d’/2).[16] Son calcul est le suivant :
Enfin une mesure complémentaire de la sensibilité est l’aire sous la courbe ROC (AUROC). Les taux de détections correctes et des fausses alarmes sont dépendants du choix du critère. La courbe ROC saisit graphiquement l’ensemble des alternatives disponibles en fonction du choix de placement du critère. En notant le taux de détections correctes (respectivement fausses alarmes) comme l’aire en dessous de la courbe de distribution du signal (respectivement du bruit) au niveau du critère :
l’AUROC se calcule comme suit :
Notons qu’une majorité d’expériences n’utilise pas une tâche de type signal/bruit mais une tâche de choix forcé à deux alternatives (2AFC). L’individu reçoit alors deux stimuli et doit déterminer lequel contient un signal spécifique. Ce cadre analytique change le calcul des paramètres de la TDS. Face à deux stimuli et devant choisir si celui de droite ou de gauche contient le signal en question, l’individu note les évidences en faveur du signal à chaque position (XD à droite et XG à gauche provenant de XS et XN). Il compare ensuite ces deux quantités d’évidence pour déterminer celle qui est la plus importante. Notons Y = XG − XD la différence entre ceux-ci. Au cours des essais SN (i.e. signal à gauche, bruit à droite), XG provient de XS et XR de XN, ainsi
et dans le cas des essais NS nous avons
Lors des essais SN, le choix est fait en fonction du critère βFC, avec une réponse gauche si Y ≥ βFC et droite sinon. Comme YSN et YNS sont les différences de deux variables aléatoires identiques, nous sommes automatiquement dans le cadre d’un modèle à variances égales. Dans ce cas, le dʹFC est calculé comme la distance entre les moyennes des variables en termes d’unité de déviation standard. Le calcul des paramètres s’obtient ici directement à partir du taux de succès pour les deux types d’essais. En notant ces taux ![]() et
et ![]() , nous avons les mesures suivantes :
, nous avons les mesures suivantes :
Avec le taux de succès global, PC, défini comme la probabilité de succès à chaque essai pondérée par la probabilité d’occurrence de deux types d’essais, la formule devient :
Notons que ce dʹFC en choix forcé est différent du dʹ précédent avec la relation suivante : dʹFC = √2dʹ. Enfin, un résultat intéressant montre que l’AUROC correspond ici à la probabilité de répondre correctement. Ainsi l’utilisation d’une tâche de choix forcés permet de calculer les paramètres de la TDS uniquement en observant les taux de succès.
Pour une présentation détaillée de l’application de la TDS au choix de type II nous renvoyons le lecteur aux présentations de Barett, Dienes et Seth (2013) et Massoni (2013). Nous ne présentons ici que les bases de la modélisation avec l’introduction des taux de fausses alarmes et de détections correctes ainsi que le dʹ de type II. En se basant sur l’hypothèse que les jugements de confiance sont basés sur les mêmes évidences que les réponses de type I, il est possible de définir des taux de détections correctes et de fausses alarmes de type II. En supposant que la réponse prend deux valeurs, R si elle est correcte et W si elle est fausse, et que la confiance est binaire, C pour confiant et U pour non-confiant, les critères de type II se définissent comme suit : β- et β+. Si les évidences sont inférieures à β- ou supérieures à β+ l’individu est confiant, autrement il est non-confiant.[17] Les taux de détections correctes et de fausses alarmes de type II sont donc H = P(C|R) et F = P(U|W). Étant données les notations précédentes, ce taux de détections correctes se calcule de la manière suivante :
Chaque terme pouvant s’exprimer par la fonction de densité gaussienne nous obtenons au final la formule suivante :
De la même manière, le taux de fausses alarmes est donné par :
Le dʹ de type II (D’) est une application directe du dʹ de type I à la décision de type II (Kunimoto, Miller et Pashler, 2001) :
Ainsi le Dʹ est défini par les valeurs du dʹ et les critères de type I et de type II.
Notes
-
[1]
Nous renvoyons le lecteur à l’ouvrage collectif de Fleming et Frith (2014) pour un aperçu des travaux les plus récents.
-
[2]
Nous définissions ici la prise de décision perceptive comme la façon dont un individu choisit une action appropriée dans une tâche de détection, de discrimination ou de catégorisation d’information sensorielle. Par oppostion, une prise de décison économique renvoie à la façon dont un individu choisit entre différentes options en fonction de ses préférences. La revue de litérature de Summerfield et Tsetsos (2012) détaille les similitudes et les oppositions entre ces deux types de décision.
-
[3]
Le lecteur intéressé par la formalisation de la TDS peut se référer à l’annexe ou aux ouvrages de Green et Swets (1966) et Wickens (2002).
-
[4]
Cette hypothèse de chaine d’évidence unique est relâchée dans les modèles à double chaine, par exemple Del Cul et al. (2009) ou les modèles hiérarchiques, par exemple Merkle, Smithson et Verkuilen (2011).
-
[5]
Nous renvoyons le lecteur à l’annexe et aux travaux de Barett, Dienes et Seth (2013) et Massoni (2013) pour une présentation détaillée.
-
[6]
Ainsi les hypothèses concernant la distribution des signaux ne sont valables que pour les réponses de type I et non de type II (gaussiennes avec variances égales – Galvin et al., 2003; Evans et Azzopardi, 2007). Il existe aussi une dépendance empirique au biais de types I et II (Evans et Azzopardi, 2007) et on observe un dʹ de type II maximal pour un niveau de sous-confiance maximale (Barett, Dienes et Seth, 2013). Enfin la possibilité d’obtenir un dʹ de type II supérieur à celui de type I (Galvin et al., 2003) pose problème.
-
[7]
Un autre problème réside dans l’utilisation de critères multiples de confiance conduisant à une multitude de courbes ROC. Ce problème peut être surmonté en calculant un critère unique basé sur la vraisemblance d’être correct (Galvin et al., 2003) ou sur le calcul de taux de détections correctes de type II maximal en fonction des fausses alarmes de type II et du critère de type I (Barett, Dienes et Seth, 2013).
-
[8]
Par exemple, Fleming et al. (2010); Massoni (2013); Fleming et al. (2014).
-
[9]
Pour une revue de littérature exhaustive se référer à Flemming et Lau (2014).
-
[10]
Par exemple, Rounis et al. (2010); Baird et al. (2013); Charles et al. (2013); Lee, Blumenfeld et d’Esposito (2013); Massoni (2014); McCurdy et al. (2013); Fleming et al. (2016).
-
[11]
Un script MATLAB pour calculer le meta-d’ est disponible à l’adresse suivante : http://www.columbia.edu/bsm2105/type2sdt/.
-
[12]
Ces règles peuvent être considérées comme des extensions de celles testées par Dienes et Seth (2010).
-
[13]
Notons aussi que ce design implique également une composante émotionnelle avec des loteries comportant des pertes et ayant de forts enjeux monétaires.
-
[14]
Nous renvoyons le lecteur à la revue de littérature de Fehr et Rangel (2011) pour l’analyse des temps de réaction en économie.
-
[15]
Cette hypothèse permet de simplifier la présentation tout en ne changeant pas l’esprit de la modélisation. Nous renvoyons le lecteur à Wickens (2002) pour les calculs des paramètres de la TDS sans cette hypothèse.
-
[16]
Une mesure alternative est la hauteur relative des deux distributions au niveau du critère :
 .
. -
[17]
Les critères de type II sont restreints à β− < β < β+.
Bibliographie
- Bahrami, B., K. Olsen, D. Bang, A. Roepstorff, G. Rees et D. Frith (2012), « What Failure in Collective Decision-Making Tells us about Metacognition », Philosophical Transactions of the Royal Society B: Biological Sciences, 367 (1594) : 1350-1365.
- Bahrami, B., K. Olsen, P.E. Latham, A. Roepstorff, G. Rees et C.D. Frith (2010), « Optimally Interacting Minds », Science, 329 (5995) : 1081-1085.
- Baird, B., J. Smallwood, K.J. Gorgolewski et D.S. Margulies (2013), « Medial and Lateral Networks in Anterior Prefrontal Cortex Support Metacognitive Ability for Memory and Perception », Journal of Neuroscience, 33 : 16657-16665.
- Bang, D., R. Fusaroli, K. Tylen, K. Olsen, P.E. Latham, J.Y.F. Lau, A. Roepstorff, G. Rees, C.D. Frith et B. Bahrami (2014), « Does Interaction Matter? Testing whether a Confidence Heuristic can Replace Interaction in Collective Decision-Making », Consciousness and Cognition, 26 : 13-23.
- Barett, A.B., Z. Dienes et A.K. Seth (2013), « Measures of Metacognition on Signal-Detection Theoretic Models », Psychological Methods, 18 (4) : 535-552.
- Bogacz, R., E. Brown, J. Moehlis, P. Holmes et J.D. Cohen (2006), « The Physics of Optimal Decision Making: a Formal Analysis of Models of Performance in Two-Alternative Forced Choice Tasks », Psychological Review, 113 (4) : 700-765.
- Brier, G.W. (1950), « Verification of Forecasts Expressed in Terms of Probability », Monthly Weather Review, 78 (1) : 1-3.
- Busemeyer, J.R. et J.T. Townsend (1993), « Decision Field Theory: a Dynamic-Cognitive Approach to Decision Making in an Uncertain Environment », Psychological Review, 100 (3) : 432-459.
- Camerer, C. et D. Lovallo (1999), « Overconfidence and Excess Entry: an Experimental Approach », The American Economic Review, 89 (1) : 306-318.
- Charles, L., F. Van Opstal, S. Marti et S. Dehaene (2013), « Distinct Brain Mechanisms for Conscious versus Subliminal Error Detection », NeuroImage, 73 : 80-94.
- David, A.S., N. Bedford, B. Wiffen et J. Gilleen (2012), « Failures of Metacognition and Lack of Insight in Neuropsychiatric Disorders », Philosophical Transactions of the Royal Society B: Biological Sciences, 367 (1594) : 1379-1390.
- Del Cul, A., S. Dehaene, P. Reyes, E. Bravo et A. Slachevsky (2009), « Causal Role of Prefrontal Cortex in the Threshold for Access to Consciousness », Brain, 132 (9) : 2531-2540.
- De Martino, B., S.M. Fleming, N. Garrett et R.J. Dolan (2013), « Confidence in Value-Based Choice », Nature Neuroscience, 16 (5787) : 105-110.
- Diederich, A. (2003), « MDFT Account of Decision Making under Time Pressure », Psychonomic Bulletin and Review, 10 (1) : 157-166.
- Dienes Z. et A.K. Seth (2010), « Gambling on the Unconscious: a Comparison of Wagering and Confidence Ratings as Measures of Awareness in an Artificial Grammar Task », Consciousness and Cognition, 19 (2) : 674-681.
- Egan, J.P. (1975), Signal Detection Theory and ROC Analysis, New York, NY : Academic Press, 277 p.
- Evans, S. et P. Azzopardi (2007), « Evaluation of a “Bias-Free” Measure of Awareness », Spatial Vision, 20 (1-2) : 61-77.
- Fehr, E. et A. Rangel (2011), « Neuroeconomics Foundations of Economic Choices – Recent Advances », Journal of Economic Perspectives, 25 (4) : 3-30.
- Fleming, S.M. et R.J. Dolan (2012), « The Neural Basis of Accurate Metacognition », Philosophical Transactions of the Royal Society B: Biological Sciences, 367 (1594) : 1338-1349.
- Fleming, S.M. et C. Frith (2014), The Cognitive Neuroscience of Metacognition, Springer-Verlag : Berlin, Heidelberg.
- Fleming, S.M. et H.C. Lau (2014), « How to Measure Metacognition », Frontiers in Human Neuroscience, 8 : 443, 2014.
- Fleming, S.M., J. Ryu, J.G. Golfinos et K. Blackmon (2014), « A Domain-Specific Impairment in Metacognitive Accuracy Following Anterior Prefrontal Lesions », Brain, 137 (10) : 2811-2822.
- Fleming, s.M., S. Massoni, t. Gajdos et j.-C. Vergnaud (2016), « Metacognition about the Past and Future: Quantifying Common and Distinct Influences on Prospective and Retrospective Judgments of Self-Performance », Neuroscience of Consciousness, 2016 (1) : niw018.
- Fleming, S.M., R.S. Weil, Z. Nagy, R.J. Dolan et G. Rees (2010), « Relating Introspective Accuracy to Individual Differences in Brain Structure », Science, 329 (5998) : 1541-1543.
- Galvin, S.J., J.V. Podd, V. Drga et J. Whitmore (2003), « Type 2 Tasks in the Theory of Signal Detectability: Discrimination between Correct and Incorrect Decisions », Psychonomic Bulletin and Review, 10 : 843-876.
- Garfinkel, S.N., A.B. Barrett, L. Minati, R.J. Dolan, A.K. Seth et H.D. Critchley (2013), « What the Heart Forgets: Cardiac Timing Influence Memory for Words and is Modulated by Metacognition and Introspective Sensitivity », Psychophysiology, 50 (6) : 505-512.
- Gold, J.I. et M.N. Shadlen (2007), « The Neural Basis of Decision Making », Annual Review of Neuroscience, 30 : 535-574.
- Green, D. M. et J. A. Swets (1966), Signal Detection Theory and Psychophysics, John Wiley and Sons.
- Harvey, N. (1997), « Confidence in Judgment », Trends in Cognitive Sciences, 1 (2) : 78-82.
- Hollard, G., S. Massoni et J.-C. Vergnaud (2016), « In Search of Good Probability Assessors: An Experimental Comparison of Elicitation Rules for Confidence Judgments », Theory and Decision, 80 (3) : 363-387.
- Kepecs, A., N. Uchida, H. Zariwala et Z.F. Mainen (2008), « Neural Correlates, Computation and Behavioural Impact of Decision Confidence », Nature, 455 (7210) : 227-231.
- Kiani, R. et M. Shalden (2009), « Representation of Confidence Associated with a Decision by Neurons in Parietal Cortex Knowledge: Some Calibration Studies », Science, 324 (5928) : 759-764.
- Koriat, A. (2012), « When are Two Heads Better than one and Why? », Science, 336 (6079) : 360-362.
- Krantz, D.H. (1969), « Threshold Theories of Signal Detection », Psychological Review, 76 (3) : 308-324.
- Kunimoto, C., J. Miller et H. Pashler (2001), « Confidence and Accuracy of Near-Threshold Discrimination Responses », Consciousness and Cognition, 10 (3) : 294-340.
- Lee, T.G., R.S. Blumenfeld et M. D’Esposito (2013), « Disruption of Dorsolateral but not Ventrolateral Prefrontal Cortex Improves Unconscious Perceptual Memories », Journal of Neuroscience, 33 : 13233-13237.
- Levitt, H. (1971), « Transformed Up-Down Methods in Psychoacoustics », Journal of the Acoustical Society of America, 49 (2) : 467-477.
- Liberman, V. et A. Tversky (1993), « On the Evaluation of Probability Judgments: Calibration, Resolution, and Monotonicity », Psychological Bulletin, 114 : 162-173.
- Lichtenstein, S., B. Fischhoff et L. Phillips (1982), « Calibration of Probabilities: the State of the Art to 1980 », inD. Kahneman, P. Slovic et A. Tversky (éds), Judgment under Uncertainty: Heuristic and Biases, Cambridge, UK : Cambridge University Press, p. 306-334.
- Luce, R.D. (1959), Individual Choice Behavior: A Theoretical Analysis, New York, NY : Wiley.
- Luce, R.D. (1963), « Detection and Recognition », in R.D. Luce, R.R. Bush et E. Galenter (éds), Handbook of Mathematical Psychology, volume 1, New York, NY : Wiley, p. 103-189.
- Luce, R.D. (1963), « A Threshold Theory for Simple Detection Experiments », Psychological Review, 70 (1) : 71-79.
- Macmillan, N.A. et C.D. Creelman (2005), Detection Theory: A User’s Guide (2nd edition), Hove, UK : Psychology Press.
- Maniscalco, B. et H. Lau (2012), « A Signal Detection Theoretic Approach for Estimating Metacognitive Sensitivity from Confidence Ratings », Consciousness and Cognition, 21 (1) : 422-430.
- Maniscalco, B. et H. Lau (2014), « Signal Detection Theory Analysis of Type 1 and Type 2 Data: Meta-d’, Response-Specific Meta-d’, and the Unequal Variance SDT Model », inS.M. Fleming et C. Frith (éds), The Cognitive Neuroscience of Metacognition, Springer : Berlin, Heidelberg, p. 25-66.
- Massoni, S., T. Gajdos et J.-C. Vergnaud (2014), « Confidence Measurement in the Light of Signal Detection Theory », Frontiers in Psychology, 5 : 1455.
- Massoni, S. et N. Roux (2014), « Optimal Group Decision: a Matter of Confidence Calibration », Mimeo.
- Massoni, S. (2013), Essays on Subjective Probabilities and Metacognition, thèse de doctorat, University of Paris 1.
- Massoni, S., « Emotion as a Boost to Metacognition: How Worry Enhances the Quality of Confidence », Consciousness and Cognition, 29 : 189-198.
- Masson, M.E.J. et C.M. Rotello (2009), « Sources of Bias in the GoodmanKruskal Gamma Coefficient Measure of Association: Implications for Studies of Metacognitive Processes », Journal of Experimental Psychology: Learning, Memory and Cognition, 35 : 509-527.
- McCurdy, L.Y., B. Maniscalco, J. Metcalfe, K.Y. Liu, F.P. de Lange et H. Lau (2013), « Anatomical Coupling Between Distinct Metacognitive Systems for Memory and Visual Perception », The Journal of Neuroscience, 33 (5) : 1897-1906.
- Merkle, E.C., M. Smithson et J. Verkuilen (2011), « Hierarchical Models of Simple Mechanisms Underlying Confidence in Decision Making », Journal of Mathematical Psychology, 55 (1) : 57-67.
- Metz, C.E. et X. Pan (1999), « Proper Binormal ROC Curves: Theory and MaximumLikelihood Estimation », Journal of Mathematical Psychology, 43 (1) : 1-33.
- Middlebrooks, P.G., Z. Abzug et M.A. Sommer (2014), « Studying Metacognitive Processes at the Single-Neuron Level », in Fleming, S.M. et C.D. Frith (éds), The Cognitive Neuroscience of Metacognition, Springer : Berlin, Heidelberg, p. 225-244.
- Murphy, A.H. (1972), « Scalar and Vector Partitions of the Probability Score: Part I. Two-State Situation », Journal of Applied Meteorology, 11 : 273-282.
- Nelson, T.O. (1984), « A Comparison of Current Measures of the Accuracy of Feeling-of-Knowing Predictions », Psychological Bulletin, 95 : 109-133.
- Nieder, A. et S. Dehaene (2009), « Representation of Number in the Brain », Annual Review of Neuroscience, 32 (1) : 185-208.
- Overgaard, M. et K. Sandberg (2012), « Kinds of Access: Different Methods for Report Reveal Different Kinds of Metacognitive Access », Philosophical Transactions of the Royal Society B: Biological Sciences, 367 (1594) : 1287-1296.
- Piazza, M., V. Izard, P. Pinel, D. Le Bihan et S. Dehaene (2004), « Tuning Curves for Approximate Numerosity in the Human Intraparietal Sulcus », Neuron, 44 (3) : 547-555.
- Pica, P., C. Lemer, V. Izard et S. Dehaene (2004), « Exact and Approximate Arithmetic in Amazonian Indigene Group », Science, 306 (5695) : 499-503.
- Pleskac, T.J. et J.R. Busemyer (2010), « Two-Stage Dynamic Signal Detection: A Theory of Choice, Decision Time, and Confidence », Psychological Review, 117 (3) : 864-901.
- Ratcliff, R. et G. McKoon (2008), « The Diffusion Decision Model: Theory and Data for Two-Choice Decision Tasks », Neural Computation, 20 (4) : 873-922.
- Ratcliff, R. et J.J. Starns (2009), « Modeling Confidence and Response Time in Recognition Memory », Psychological Review, 116 (1) : 59-83.
- Ratcliff, R. (1978), « A Theory of Memory Retrieval », Psychological Review, 85 (2) : 59-108.
- Rounis, E., B. Maniscalco, J.C. Rothwell, R.E. Passingham et H. Lau (2010), « Theta-Burst Transcranial Magnetic Stimulation to the Prefrontal Cortex Impairs Metacognitive Visual Awareness », Cognitive Neuroscience, 9 (8) : 165-175.
- Savage, L.J. (1954), The Foundations of Statistics, New York, NY : John Wiley and Sons.
- Sorkin, R.D., C. J. Hays et R. West (2001), « Signal Detection Analysis of Group Decision Making », Psychological Review, 108 : 183-203.
- Summerfield, C. et K. Tsetsos (2012), « Building Bridges between Perceptual and Economic Decision-Making: Neural and Computational Mechanisms », Frontiers in Neuroscience, 6 (70) : 1-20.
- Wallsten, T.S. et D.V. Budescu (1983), « Encoding Subjective Probabilities: a Psychological and Psychometric Review », Management Science, 29 (2) : 151-173.
- Wickens, T.D. (2002), Elementary Signal Detection Theory, New-York, NY : Oxford University Press.
- Yaniv, I., F. Yates et K. Smith (1991), « Measures of Discrimination Skill in Probabilistic Judgment », Psychological Bulletin, 110 (3) : 611-617.
- Yates, J.F. (1982), « External Correspondence: Decompositions of the Mean Probability Score », Organizational Behavior and Human Performance, 30 (1) : 132-156.
- Yeung, N. et C. Summerfield (2012), « Metacognition in Human Decision-Making; Confidence and Error Monitoring », Philosophical Transactions of the Royal Society B: Biological Sciences, 367 (1594) : 1310-1321.
List of figures
Graphique 1
Deux types de distributions du signal et du bruit
Graphique 2
Deux types de critères décisionnels
Graphique 3
Relations entre les différents types de réponse et le placement du critère décisionnel
a
b
Note : (a) Courbes ROC en fonction de différents dʹ. La partie grisée correspond au critère inférieur à 1. Ainsi les points A et B représentent des stratégies respectivement prudente et risquée pour un même dʹ de 1. (b) Courbe ROC pour un même dʹ en fonction de différents niveaux de critères.
Graphique 5
Critères décisionnels de la confiance en fonction des distributions du signal et du bruit
Note : Les mêmes évidences sont utilisées pour prendre la décision de type I et de type II. Chaque critère représente ici un niveau de confiance avec une symétrie de ces niveaux par rapport au critère de type I c’est-à-dire (S1,1) et (S2,1) correspondent à une confiance de 1 (sur une échelle de 1 à 4) respectivement pour le stimulus 1 et le stimulus 2.
A
B
C
Note : (A) Exemple de stimuli perceptifs. (B) Règle d’élicitation de la confiance dite de matching probabilities. (C) Exemple d’un essai complet avec fixation, stimulus, choix de type I et de type II.
Graphique 7
Dissociation entre la sensibilité métacognitive et le biais métacognitif