Abstracts
Résumé
L’objectif de cet article est de présenter un modèle synthétique de taux de change réel d’équilibre de type « NATural Real EXchange rate » pour une petite économie « développée » et ouverte mais confrontée à des marchés de capitaux imparfaits. Conformément à la tradition NATREX, le taux de change réel d’équilibre dépend de l’horizon temporel considéré. À moyen terme, il est déterminé, dans le cadre d’un équilibre de flux, conjointement par un ensemble de fondamentaux réels (la productivité globale, la demande étrangère, les termes de l’échange, le taux d’intérêt réel, la préférence pour le présent et les dépenses publiques) et de variables prédéterminées (le capital productif et la dette externe). À long terme, par contre, des ajustements de nature stock-flux, liés aux mouvements endogènes des variables prédéterminées, entrent en jeu. Le taux de change réel d’équilibre ne dépend plus alors que des seuls fondamentaux réels. Par ailleurs, cette présentation fait ressortir l’importance de certains paramètres structurels du modèle, à savoir l’effet richesse, l’élasticité des importations par rapport à l’investissement national et le degré de mobilité internationale des capitaux.
Abstract
This article presents a synthetic model of the « NATural Real EXchange rate » approach for a small open « developed » economy constrained by an imperfect international capital mobility. In accordance with the conventional NATREX wisdom, the determination of the equilibrium real exchange rate obviously depends on the time horizon considered. In the medium run, the equilibrium value results from both the real fundamentals (global productivity, foreign demand, terms of trade, real interest rate, time preference and government spending) and the predetermined variables (productive capital and external debt). In the long run, the stock-flow dynamics linked to the endogenous adjustments of the predetermined variables come into action. Thereafter, the equilibrium real exchange rate is only impacted by the real fundamentals. Moreover, the model puts forward the crucial role of some structural parameters, namely the wealth effect, the import elasticity of national investment and the degree of international capital mobility.
Article body
Introduction
Ces 30 dernières années de crises économiques et financières auront au moins servi à faire ressortir un constat implacable. Le système monétaire international fonctionne mal et la nécessité de sa réforme urgente ne fait plus aujourd’hui aucun doute (Bergsten et al., 1999; Cartapanis, 2004). L’une des manifestations les plus évidentes de ce dysfonctionnement est la récurrence des situations de distorsions de change ou encore de « mésalignement réel », lesquelles peuvent être à l’origine de perturbations importantes de l’économie[1]. Concrètement le mésalignement réel d’une monnaie représente les écarts soutenus du taux de change réel courant par rapport à son niveau d’équilibre de long terme. Aussi toute évaluation crédible du mésalignement réel ne peut faire l’économie d’une réflexion préalable sur le problème de détermination des taux de change réels d’équilibre.
La théorie la plus couramment utilisée dans ce domaine est la parité des pouvoirs d’achat [PPA] (Cassel, 1925). Celle-ci définit le niveau du taux de change nominal d’équilibre comme le taux assurant la parité de pouvoir d’achat entre deux monnaies, de telle sorte qu’une unité de monnaie domestique puisse être échangée contre la même quantité de biens dans son pays d’origine ou dans tout autre pays après conversion en monnaie locale. Toutefois, qu’elle soit prise dans sa version absolue ou relative[2], la théorie de la PPA présente des défauts majeurs, tant au niveau conceptuel qu’au niveau empirique, qui ne lui permettent pas d’analyser correctement les mouvements de moyen à long terme des taux de change réels (Isard, 1997; MacDonald, 1999; Darné et Hoarau, 2008).
La seconde théorie explicative des taux de change réels d’équilibre est l’approche microéconomique (Joly et al., 1996; Hinkle et Montiel, 1999; Hoarau, 2009). Elle montre en particulier que si la PPA est effectivement susceptible d’être valide pour les biens faisant l’objet du commerce international, elle n’a aucune raison de l’être pour les biens du secteur abrité de la concurrence internationale, c’est-à-dire les biens non échangeables. Par conséquent, les fluctuations constatées dans le taux de change réel ne peuvent provenir que des modifications du prix relatif des biens échangeables par rapport aux biens non échangeables. Il est donc considéré dans sa dimension de prix relatif interne dont l’ajustement permet l’allocation des ressources entre les secteurs des biens échangeables et des biens non échangeables. Ainsi, le taux de change réel, qui est maintenant fonction d’un ensemble de déterminants fondamentaux, peut faire l’objet d’une analyse microéconomique rigoureuse dans le cadre d’un modèle d’équilibre général intertemporel. Toutefois, sa validité repose fondamentalement sur la loi du prix unique, et donc sur la PPA, sur le secteur des biens échangeables. Or, de nombreux éléments viennent remettre en cause cette hypothèse parmi lesquels l’imparfaite substituabilité des biens soumis à la concurrence internationale. Deux enseignements en découlent. D’une part, le taux de change réel d’équilibre doit prendre en compte les déterminants du prix relatif des biens échangeables entre pays. D’autre part, la faiblesse des élasticités prix du commerce extérieur qui résulte de l’hétérogénéité des biens échangeables, implique que la balance commerciale devient relativement insensible aux variations du taux de change réel. La détermination du taux de change réel d’équilibre de long terme doit donc reposer sur la double analyse des marchés des biens et des capitaux.
C’est l’optique retenue par l’approche macroéconomique. Celle-ci considère le taux de change réel (e) comme un indicateur de la compétitivité-prix globale d’une économie, avec ![]() [3]. Elle définit ensuite son niveau d’équilibre comme celui qui permet, parallèlement à la réalisation de l’équilibre interne, de garantir, à moyen et long terme, la compatibilité entre le solde courant et le solde des flux de capitaux structurels (investissements directs à l’étranger, investissements de portefeuille à long terme). Cette approche générale est particulièrement attrayante car elle permet de distinguer plusieurs concepts d’équilibre selon l’horizon temporel considéré.
[3]. Elle définit ensuite son niveau d’équilibre comme celui qui permet, parallèlement à la réalisation de l’équilibre interne, de garantir, à moyen et long terme, la compatibilité entre le solde courant et le solde des flux de capitaux structurels (investissements directs à l’étranger, investissements de portefeuille à long terme). Cette approche générale est particulièrement attrayante car elle permet de distinguer plusieurs concepts d’équilibre selon l’horizon temporel considéré.
La parité réelle d’équilibre peut être d’abord envisagée dans une perspective de moyen terme (sur l’horizon de la politique économique) dans le cadre d’un modèle d’équilibre en flux de type « Fundamental Equilibrium Exchange Rate » [FEER]. À cet effet, elle s’intéresse particulièrement aux problèmes du financement du déséquilibre externe et de l’évaluation des flux de capitaux compatibles avec la soutenabilité de la position extérieure nette. Par ailleurs, elle peut reposer soit sur des objectifs de politique économique (Williamson, 1985, 1994), soit sur la politique économique en vigueur (Isard et Faruqee, 1998; Faruqee et al., 1999), relatifs aux équilibres interne et externe.
Ensuite, elle peut être envisagée dans une perspective de long terme dans le cadre d’un modèle stock-flux de type « NATural Real Exchange Rate » [NATREX] (Stein, Allen et al., 1995; Stein, 1999; Marin Martinez, 2003; Stein 2006). Ce dernier considère que la spécification en termes de flux du FEER réduit la portée de l’analyse essentiellement au moyen terme. En effet, la fixation de la cible de compte courant à un solde de flux de capitaux sous-jacents non nul introduit des effets dynamiques, absents du modèle initial. Par la suite, la présence d’effets de stock et la modification perpétuelle de l’équilibre externe induite nécessitent une détermination du taux de change réel d’équilibre qui soit résolument dynamique et compatible avec la réalisation de l’état stationnaire stable d’un modèle macroéconomique. Toujours dans une perspective de long terme, d’autres travaux (Clark et MacDonald, 1999, 2000), en fondant le modèle « Behavioral Equilibrium Exchange Rate » [BEER], ont choisi de retenir une approche moins structurelle et tournée vers l’empirisme, afin de prendre en compte simultanément dans la détermination du change de référence les facteurs fondamentaux du prix relatif des biens échangés (entre pays) et du prix relatif des biens échangés en termes de biens non échangés (à l’intérieur de chaque pays).
Parmi cet ensemble de modèles du taux de change réel d’équilibre, l’approche du NATREX apparaît comme la plus aboutie, au moins sur le plan théorique[4], dans le sens où elle permet d’étudier de manière claire et rigoureuse les effets des déterminants fondamentaux sur la parité de référence à chaque étape de son évolution (Rey, 2009). Il peut se définir simplement comme « the equilibrium real exchange rate that clears the balance of payments in the absence of cyclical factors, speculative capital flows, and movements in international reserves » (Allen, 1995 : 6). En d’autres termes, le NATREX détermine la parité réelle compatible à la fois avec l’équilibre interne, assimilé au taux de chômage naturel, et l’équilibre externe, identifié à l’équilibre de la balance des paiements à moyen terme, c’est-à-dire en faisant abstraction des changements des réserves internationales et des flux de capitaux de court terme (Stein et Paladino, 2001).
Néanmoins, faire une présentation exhaustive de ce concept reste un exercice délicat. En effet, celui-ci est une famille de modèles plutôt qu’un modèle unique, tous animés par la même logique sous-jacente, mais se distinguant par la nature de l’économie représentée (Allen, 1995; Federici et Gandolfo, 2002). Les modèles relatifs au NATREX peuvent être regroupés en deux catégories selon la position du pays étudié sur les marchés internationaux. Certains travaux s’intéressent au cas d’un « grand pays », lequel, en présence de parfaite mobilité internationale des capitaux, est capable d’agir sur ses termes de l’échange[5] et sur le taux d’intérêt réel mondial. Dans ce cas, la modélisation complète du pays étranger devient indispensable (Stein, 1995; Belloc et Federici, 2010). D’autres se focalisent sur le cas du « petit pays ». À l’intérieur de ce cadre général, deux types d’approche sont envisagés selon le degré de mobilité des capitaux au niveau international. Lorsque celle-ci est parfaite, le modèle suppose que la petite économie ouverte, qualifiée ici de « développée », peut emprunter sans limite au taux d’intérêt réel mondial exogène (Crouhy-Veyrac et Saint-Marc, 1995; Song, 1997). Lorsque celle-ci est imparfaite, la petite économie ouverte, qualifiée dans ce cas d’« économie en développement », est contrainte sur les marchés internationaux de capitaux. Son taux d’intérêt réel est alors égal au taux mondial exogène plus une prime de risque (Lim et Stein, 1995; Artus, 1998; You et Sarantis, 2008a)[6]. Quel que soit le cas envisagé, seule la modélisation du petit pays est utile et les variables définissant le reste du monde sont considérées comme exogènes.
Toutefois, aucune approche n’a envisagé jusqu’à présent la configuration d’une petite économie « développée » endettée devant faire face à des marchés de capitaux internationaux contraints. Pourtant, la sévérité de la crise financière récente a révélé la fragilité financière de plusieurs économies développées telles la Grèce, l’Espagne ou encore le Portugal. C’est précisément dans cette perspective que notre présent article s’inscrit. Nous nous proposons d’établir un modèle synthétique capable d’intégrer et de formaliser l’ensemble des résultats pertinents découlant de la modélisation du NATREX pour une petite économie « développée » ouverte confrontée à des marchés de capitaux imparfaits. Nous verrons que les caractéristiques structurelles de ce type d’économies (croissance démographique nulle, position débitrice nette, prédominance du secteur moderne, forte ouverture aux échanges extérieurs, price taker sur les marchés mondiaux, croissance économique faible, dette libellée en monnaie domestique, préférence pour les biens de consommation domestiques,...) ne sont pas sans influence sur la détermination du taux de change réel d’équilibre.
Aussi, nous choisissons d’organiser la suite de notre article de la manière suivante. La première section expose un modèle canonique d’une petite économie développée ouverte en considérant à la fois les situations de parfaite et d’imparfaite mobilité internationale des capitaux. Les sections 2 et 3 mettent en évidence les solutions statiques du modèle, c’est-à-dire les taux de change réel d’équilibre de moyen terme et de long terme. La section 4 étudie les mécanismes d’ajustement dynamique. Enfin, la dernière section conclut en insistant sur la portée du modèle dans le domaine de la politique économique.
1. La structure du modèle NATREX
Le modèle est écrit en termes réels et admet l’hypothèse d’une petite économie ouverte produisant et échangeant un bien imparfaitement substituable avec le reste du monde. Les variables définissant ce dernier sont donc considérées comme exogènes. Nous supposons également que les variables sont exprimées par habitant de travailleurs actifs, que le taux de croissance de la population est nul, que le pays est débiteur net et que les capitaux sont imparfaitement mobiles au niveau international. D’autres caractéristiques seront introduites lors de la présentation des relations structurelles concernées. Au total, la structure du modèle fait apparaître deux blocs, en l’occurrence les relations d’équilibre fondamental et dynamiques[7].
1.1 Équilibre fondamental et balance des paiements
Notre modèle de taux de change réel d’équilibre s’appuie sur la relation d’équilibre fondamental donnée par l’identité traditionnelle des comptes nationaux lorsque l’équilibre interne est réalisé, c’est-à-dire lorsque la production nationale est égale à son potentiel :
L’équation (1), où ka représente le compte des capitaux et ca le compte courant, est particulière car elle traduit deux équilibres à la fois. En effet, dans un premier temps, elle décrit la condition d’équilibre de la balance des paiements. En supposant que i – s (investissement national désiré moins épargne nationale désirée) représente les flux d’entrée nets de capitaux, c’est-à-dire le compte de capitaux, la relation (1) devient :
Cet équilibre signifie que les déficits courants doivent être financés par les flux d’entrée nets de capitaux. La vision du change adoptée est par conséquent résolument positive. En effet, pour définir les flux de capitaux, aucune hypothèse n’est faite sur des niveaux cibles ou des objectifs de politique économique à atteindre. Elle s’appuie simplement sur les valeurs constatées de l’épargne et de l’investissement.
Dans un deuxième temps, en se référant à la définition de l’utilisation du revenu (3) et aux composantes du compte courant (4), l’équilibre fondamental peut s’interpréter comme la condition d’équilibre du marché des biens et services (5).
et
avec y la production domestique, cs la consommation sociale ou nationale, rf le paiement des intérêts sur la dette extérieure, r le taux d’intérêt réel domestique, f la dette extérieure libellée en monnaie domestique, b le solde commercial et g les dépenses publiques. Notons que la consommation nationale a été décomposée en ses parties privée (c) et publique (g) en posant cs = c + g. Il convient à présent de définir explicitement l’ensemble des arguments de cette relation (5).
1.1.1 La production domestique
Le côté offre du modèle est représenté simplement par la production domestique (y). Celle-ci est définie par l’équation (6) comme une fonction croissante de la productivité globale des facteurs (u) et du capital productif (k). La forme retenue de type « Cobb-Douglas » pour la fonction de production indique que cette dernière respecte les trois propriétés d’une fonction de production de type néoclassique à savoir une productivité marginale du capital décroissante, des rendements d’échelle constants et le respect des conditions d’Inada[8].
1.1.2 Consommation privée et consommation publique
Dans la théorie NATREX, le niveau de consommation sociale (privée plus publique) (cs) optimal est choisi en maximisant une fonction d’utilité intertemporelle (V) sous contrainte budgétaire donnée par l’accumulation des avoirs extérieurs nets (a) et compte tenu du taux d’actualisation (ρ) qui représente également la préférence pour le présent. Le programme, résolu par les techniques de programmation dynamique optimale en situation d’incertitude (Fleming et Zariphopoulou, 1991), est le suivant :
où Λ donne la valeur actualisée du prix implicite du revenu. Ensuite, en supposant une élasticité de substitution intertemporelle unitaire et en prenant une forme fonctionnelle simple pour la fonction d’utilité (V(cs) = ln(cs)), il découle le montant de la consommation instantanée, soit :
Maintenant, en supposant que le stock de capital actuel (k) représente la somme des revenus nationaux futurs actualisés au taux d’intérêt courant et en posant la dette extérieure (f) comme l’opposé de l’avoir extérieur net, il vient w̅ = k –f. Il est possible finalement de déduire la fonction de consommation nationale :
Au final, la fonction de consommation dépend positivement du taux de préférence pour le présent et de la richesse nette (w). Notons cependant que cette spécification ne permet pas d’isoler le rôle spécifique de la consommation publique. Or, il apparaît clairement qu’au cours des 30 dernières années, l’essentiel des variations du taux d’épargne global a été le fruit d’importants changements d’orientation des politiques budgétaires (Artus, 1998). Ce dernier propose donc la spécification amendée (7), exprimée par habitant et sous forme linéarisée, qui a l’avantage de faire apparaître explicitement le secteur public et l’impact de ce dernier sur les choix de consommation des agents privés. À l’image de ce qui est communément retenu dans la modélisation NATREX (Belloc et Federici, 2010), nous considérons qu’il n’y a pas d’équivalence ricardienne dans la mesure où par hypothèse le consommateur représentatif ne peut prévoir le futur correctement. Celle-ci est fonction du revenu disponible (yd), de la richesse (w) et de la préférence pour le présent[9] (ρ). Ces trois variables ont une influence positive sur les décisions des ménages.
Le revenu disponible (yd) est donné par la différence entre le revenu national[10] (y) et un impôt forfaitaire prélévé par l’État (t), d’où yd = y – t. La richesse est définie par l’équation (8). Elle réagit positivement par rapport au capital productif (k) et négativement par rapport à la dette extérieure (f). La dette extérieure étant libellée en monnaie nationale, sa valeur pour les ménages domestiques est indépendante des variations de taux de change réel.
Il est possible alors de réexprimer la fonction de consommation en substituant dans l’équation (7), la production et la richesse par leurs valeurs données respectivement par (6) et (8) :
Il apparaît de cette dernière équation que la consommation des ménages est une fonction décroissante de la dette externe. En effet, quand la dette augmente, la richesse nette diminue, ce qui décourage la consommation privée[11].
Les dépenses publiques (g), données par (9), sont considérées comme étant exogènes. Étant donné que l’hypothèse d’équivalence ricardienne n’est pas retenue, les ménages ne compensent pas entièrement les variations des dépenses publiques, celles-ci vont avoir des effets significatifs sur le secteur réel de l’économie. De plus, nous faisons l’hypothèse que le budget public est équilibré quelle que soit la période retenue[12].
1.1.3 Investissement domestique et activité économique
La fonction d’investissement du NATREX s’appuie sur le concept de « profitabilité » developpé par Tobin (1969) ou encore appelé le q de Tobin[13]. Elle adopte en fait une interprétation résolument microéconomique du coefficient q en le redéfinissant comme le rapport entre la valeur acquise par une unité additionnelle de capital, c’est-à-dire l’espérance de la valeur actualisée de tous les flux de revenus qu’elle procure, et le prix de vente de cette unité avant sa mise en place, c’est-à-dire son coût d’achat. Étant donné que les flux futurs de revenus correspondent à la valeur de la productivité marginale physique du capital, le coefficient q de Tobin s’écrit :
où Px, Pk et E sont respectivement les prix du bien final[14], du bien capital et l’espérance mathématique. De par la forme de notre fonction de production donnée par (6), l’expression de la productivité marginale du capital ![]() est :
est :
De plus, si nous supposons que le bien capital est composé d’une proportion a de bien produit au prix Px et d’une proportion 1 – a de bien importé au prix Pm, le prix du bien capital s’écrit :
Si nous substituons les expressions de la productivité marginale du capital, du prix du capital et des termes de l’échange ![]() dans la définition du coefficient q, il vient :
dans la définition du coefficient q, il vient :
d’où la fonction d’investissement domestique :
Le coefficient q, qui détermine le niveau d’investissement, dépend positivement des termes de l’échange, de la productivité globale du capital et négativement du stock de capital et du taux d’intérêt réel domestique[15]. Néanmoins, cette spécification demeure incomplète dans la mesure où elle ne fait aucunement référence à l’état de l’activité économique et à l’influence de l’évolution de la demande sur les décisions d’investissement, c’est-à-dire les contraintes de débouchés perçues ou anticipées par la firme locale. Or, une capacité de production importante permet de répondre à la demande en cas de bonne conjoncture, mais reste sous-utilisée en cas de mauvaise conjoncture. Face à une demande incertaine, les firmes acceptent d’autant plus ce risque de surcapacité que la profitabilité de l’investissement est forte dans les bons états. Par conséquent, le coefficient q et la profitabilité ne doivent pas seulement refléter des indicateurs financiers ou de rentabilité de l’investissement, mais incorporer plus généralement toutes les contraintes perçues ou anticipées par l’entreprise, parmi lesquelles les contraintes de débouchés (Malinvaud, 1987). En s’inspirant du modèle IS-LM-BP, Hoarau (2004) propose de retenir une fonction d’investissement (11) qui incorpore, parallèlement à la composante q traditionnelle, une composante qui illustre les perspectives de débouchés aussi bien sur le marché domestique qu’à l’extérieur, soit :
avec yw et y représentant respectivement l’état de la demande étrangère et locale. Soit sous forme linéaire :
L’évaluation d’un projet d’investissement repose désormais sur deux éléments. D’une part, elle tient compte de manière positive de la comparaison entre la productivité marginale et le coût marginal du capital, augmentée de l’impact des termes de l’échange. D’autre part, elle intègre l’influence de l’activité économique de telle sorte qu’une hausse de la demande étrangère et domestique, en élargissant les perspectives de débouchés pour les firmes locales, stimule l’investissement.
1.1.4 Une demande nette d’exportations
La balance commerciale, donnée par l’équation (12), est représentée par la différence entre les exportations (x) et les importations (m), c’est-à-dire b = x – m. Les exportations dépendent positivement de la demande étrangère (yw) et de la compétitivité extérieure de l’économie nationale résumée par le taux de change réel ![]() [16] et les termes de l’échange exogènes. Les importations sont une fonction croissante de l’absorption domestique, c’est-à-dire la consommation plus l’investissement. Nous supposons ici qu’il existe une certaine préférence pour les biens de consommation domestique de telle sorte que l’élasticité des importations par rapport à la consommation (λ3) est relativement faible. Elles dépendent aussi de façon négative du taux de change réel puisqu’une hausse de ce dernier signifie un renchérissement des produits étrangers. Par conséquent, l’impact du taux de change réel sur la balance commerciale est complexe. Nous choisissons de l’introduire simplement par l’intermédiaire du terme
[16] et les termes de l’échange exogènes. Les importations sont une fonction croissante de l’absorption domestique, c’est-à-dire la consommation plus l’investissement. Nous supposons ici qu’il existe une certaine préférence pour les biens de consommation domestique de telle sorte que l’élasticité des importations par rapport à la consommation (λ3) est relativement faible. Elles dépendent aussi de façon négative du taux de change réel puisqu’une hausse de ce dernier signifie un renchérissement des produits étrangers. Par conséquent, l’impact du taux de change réel sur la balance commerciale est complexe. Nous choisissons de l’introduire simplement par l’intermédiaire du terme ![]() qui représente le pouvoir d’achat en devises d’un revenu national de ε. Cela permet d’obtenir un équilibre du marché des biens et services qui soit linéaire (Artus, 1998). En définitive, nous supposons que la condition de Marshall-Lerner-Robinson généralisée est vérifiée, ce qui implique que le taux de change réel exerce un effet positif sur la balance commerciale.
qui représente le pouvoir d’achat en devises d’un revenu national de ε. Cela permet d’obtenir un équilibre du marché des biens et services qui soit linéaire (Artus, 1998). En définitive, nous supposons que la condition de Marshall-Lerner-Robinson généralisée est vérifiée, ce qui implique que le taux de change réel exerce un effet positif sur la balance commerciale.
Cette dernière relation montre bien que le taux de change réel occupe une place centrale dans le modèle. En effet, il doit permettre à la balance commerciale de s’ajuster pour résorber un éventuel déséquilibre entre la production et l’absorption domestiques.
1.2 Les relations dynamiques
Le modèle introduit trois variables dynamiques, à savoir le stock de capital productif (k), le stock de dette extérieure (f) et le taux de change réel.
1.2.1 Variables prédéterminées et dynamique de l’économie
Les variables prédéterminées sont caractéristiques des modèles de change réel d’équilibre puisqu’elles définissent, conjointement avec les fondamentaux réels, la dynamique du taux de change réel d’équilibre. Ces variables sont le capital par habitant (k) et la dette extérieure nette (f). Par hypothèse, à court et moyen terme, leur niveau est considéré comme donné, c’est-à-dire elles sont exogènes. Toutefois, durant la transition du moyen au long terme, le capital productif et la dette deviennent endogènes et varient en fonction des perturbations constatées dans les fondamentaux, par le biais des fonctions d’investissement et de compte courant. Finalement, à long terme, ces deux variables convergent vers leur niveau d’état stationnaire déterminé par les variables fondamentales.
Par conséquent, la prise en compte de leur évolution du moyen au long terme donne une dimension dynamique au modèle. Étant donné que les différentes variables sont exprimées par habitant et que le taux de croissance de la population est nul, l’accumulation du stock de capital productif (11), en l’absence de dépréciation de ce dernier, est définie simplement par la fonction d’investissement, telle que :
La dynamique de la dette extérieure, donnée par (13), est représentée par l’écart entre l’investissement et l’épargne désirés du pays considéré, c’est-à-dire les flux d’entrée nets de capitaux :
L’accumulation de la dette extérieure correspond donc simplement au déficit de compte courant. C’est une fonction croissante de r et de f, et décroissante de b.
1.2.2 Taux d’intérêt réel, équilibre de portefeuille et imparfaite mobilité des capitaux
En définitive, le modèle est bouclé par la dynamique du taux de change réel. Elle se déduit de la condition d’équilibre de portefeuille avec imparfaite mobilité des capitaux :
Ensuite, en exprimant de nouveau cette relation par rapport au taux d’intérêt réel domestique, il vient :
Cette formulation nous indique que le taux d’intérêt réel domestique est composé d’une part de sa partie non couverte, c’est-à-dire le taux d’intérêt réel étranger (rw) ajusté de l’anticipation d’une dépréciation du change ![]() , et d’autre part du terme supplémentaire
, et d’autre part du terme supplémentaire ![]() . Le paramètre θ représente le degré de mobilité internationale des capitaux et
. Le paramètre θ représente le degré de mobilité internationale des capitaux et ![]() la valeur en devises de la dette extérieure du pays considéré. De plus, si nous postulons les hypothèses d’anticipations rationnelles (E[e] = e) et de prévision parfaite, à l’état stationnaire de la dynamique du change réel (E[ė] = 0), l’expression (14) devient :
la valeur en devises de la dette extérieure du pays considéré. De plus, si nous postulons les hypothèses d’anticipations rationnelles (E[e] = e) et de prévision parfaite, à l’état stationnaire de la dynamique du change réel (E[ė] = 0), l’expression (14) devient :
Dès lors, il en découle que la valeur prise par θ, c’est-à-dire l’hypothèse faite sur la mobilité des capitaux, revêt une importance non négligeable dans le processus de détermination de l’équilibre[17].
2. Le taux de change réel d’équilibre de moyen terme
À tout instant, il existe un taux de change réel d’équilibre de court terme qui correspond à la solution du modèle Mundell-Fleming. Il se déduit de la combinaison des équilibres du marché des biens et services, du marché des titres et du marché des changes. À cette échéance, les prix sont généralement rigides et la production ne se fixe pas automatiquement à son niveau de plein emploi. Le taux de change réel d’équilibre de court terme est donc fonction des différentes variables agissant sur ces équilibres, à savoir les fondamentaux exogènes à l’économie nationale, les variables prédéterminées (la dette et le capital productif donnés à court terme) et les variables jouant sur les anticipations des agents. Toutefois, notre travail ne porte pas sur la formation de l’équilibre de court terme[18]. Dans l’esprit des théories du taux de change réel d’équilibre, nous considérons seulement les horizons de moyen et long terme.
À moyen terme, l’équilibre externe se définit comme la condition de soutenabilité des paiements extérieurs. Les déficits de compte courant doivent être financés par des flux d’entrée nets de capitaux soutenables. Par conséquent, dans ce contexte, le compte courant plus l’investissement moins l’épargne, évalués au plein emploi et en respectant l’équilibre de portefeuille, doit être égal à zéro, c’est-à-dire c’est la relation (2). La spécificité de l’analyse de moyen terme provient de l’hypothèse faite sur la vitesse de convergence des variables prédéterminées. En effet, nous supposons que celles-ci possèdent une vitesse d’ajustement relativement lente. En définitive, le taux de change réel d’équilibre de moyen terme est celui associé aux équilibres interne et externe sachant que les stocks de capital productif et de dette extérieure sont donnés à cette échéance. Le NATREX de moyen terme se déduit alors de l’équilibre du marché global des biens et services. La demande extérieure nette, représentée par la balance commerciale, va s’ajuster par le biais du taux de change réel dès qu’il y a un déséquilibre entre l’offre et l’absorption nationale. Par ailleurs, puisqu’il y a imparfaite mobilité des capitaux, ce mécanisme est perturbé par l’ajustement simultané du taux d’intérêt réel domestique.
2.1 Équilibre stationnaire et instabilité dynamique du change réel
Après avoir introduit la condition d’équilibre de portefeuille dans l’équation (5) et identifié chaque variable, l’équilibre du marché des biens et services peut se réécrire comme :
À partir de cette relation, la dynamique du change réel par rapport à ces déterminants de moyen terme peut être dégagée.
Comme il a été précisé plus haut, le taux de change réel d’équilibre de moyen terme (ẽ) est la parité réelle stationnaire qui réalise l’équilibre du marché des biens et services. Ainsi, après avoir identifié au préalable la production nationale dans (16), nous déduisons ẽ pour ė = 0 tel que :
avec
À moyen terme, le taux de change réel d’équilibre est donc fonction des fondamentaux réels domestiques (la productivité globale, la préférence pour le présent et les dépenses publiques), étrangers (le taux d’intérêt réel mondial, les termes de l’échange et la demande mondiale) et des niveaux donnés des variables de stock (le capital productif et la dette extérieure).
Il convient ensuite d’étudier la stabilité de cet équilibre dynamique. Par souci de simplification, l’expression (16) se réécrit sous la forme suivante :
La condition de stabilité dynamique à moyen terme se déduit de la dérivée de ė par rapport à e, c’est-à-dire :
Le signe de z va nous renseigner sur la stabilité du système. Si z < 0, cela implique que, suite à un choc, le taux de change réel revient automatiquement vers l’équilibre stationnaire, c’est-à-dire l’équilibre ẽ est stable. Au contraire, si z > 0 , suite à un choc, le taux de change réel va s’éloigner et ne plus revenir vers l’équilibre stationnaire, c’est-à-dire l’équilibre ẽ est instable. Dans ce dernier cas, la seule solution stable est l’équilibre stationnaire. D’après l’équation (18), ![]() peut se réécrire comme :
peut se réécrire comme :
Ce qui nous donne finalement l’expression suivante pour z :
La dynamique du change réel révèle sa nature instable à moyen terme. Il n’existe donc qu’une seule solution stable et le taux de change réel saute instantanément sur son point d’équilibre stationnaire. Ce résultat se justifie par le fait que le stock de capital productif et de dette extérieure ne se sont pas encore ajustés à leur état stationnaire. Nous retrouvons là une des conclusions principales des modèles de taux de change réel d’équilibre. Ce dernier n’est pas un point mais une trajectoire de moyen à long terme convergeant vers l’état stationnaire de l’économie.
2.2 L’impact des déterminants fondamentaux : les effets directs
Afin d’identifier les effets directs découlant des fondamentaux de l’économie, nous supposons pour le moment que la mobilité des capitaux est parfaite, d’où θ = 0. Les résultats pour θ ≠ 0 sont présentés dans la section 2.3.
2.2.1 La demande étrangère
Notre modèle révèle que l’impact de la demande étrangère sur le taux de change réel à moyen terme doit être décomposé en deux canaux.
Le premier canal, de nature externe, regroupe deux effets très différents. D’abord, une hausse de yw entraîne une augmentation des exportations, ce qui améliore la balance commerciale et pousse le change réel d’équilibre à s’apprécier. Ensuite, cette même hausse de yw stimule l’investissement domestique, ce qui provoque une augmentation des importations et une détérioration de la balance commerciale. Ce deuxième effet implique une dépréciation réelle d’équilibre. En définitive, l’impact sur le taux de change réel dépend de l’influence globale exercée par la demande mondiale sur la balance commerciale, et en particulier du degré de dépendance de l’économie locale par rapport à l’étranger en matière d’investissement (si les investissements sont massivement importés), c’est-à-dire le paramètre λ4. En dérivant l’expression de la balance commerciale (12) par rapport à yw, nous obtenons :
Par conséquent, la demande étrangère améliore (détériore) la balance commerciale si et seulement si l’élasticité des importations par rapport à l’investissement domestique (λ4) est inférieure au rapport des élasticités des exportations et des investissements par rapport à la demande étrangère ![]() [19].
[19].
Le deuxième canal est d’ordre interne. En effet, une hausse de la demande mondiale en stimulant l’investissement national entraîne un gonflement de l’absorption domestique. L’accroissement de la demande interne qui en découle implique une appréciation du taux de change réel d’équilibre pour résorber l’excès de demande et rétablir l’équilibre sur le marché des biens et services.
Au final, l’effet global sur le taux de change réel d’équilibre à moyen terme ![]() est indéterminé et tout dépendra de l’importance du paramètre λ4 :
est indéterminé et tout dépendra de l’importance du paramètre λ4 :
Cette inégalité signifie simplement qu’une hausse de la demande étrangère apprécie (déprécie) le change réel si et seulement si la part des investissements domestiques dans les importations nationales est relativement faible (forte).
2.2.2 La productivité globale des facteurs
L’effet total de la productivité globale des facteurs est donné par la dérivée de l’expression du taux de change réel d’équilibre par rapport à u, soit :
Par conséquent, l’impact de la productivité globale peut être décomposé en deux canaux de transmission, exerçant des effets opposés sur le change réel d’équilibre.
Le premier agit à travers l’épargne nationale (![]() ). Une hausse de la productivité provoque à la fois une hausse de la production et de la consommation. Toutefois, puisque la propension marginale à consommer (β1) est inférieure à l’unité, l’effet sur l’offre domine, ce qui met une pression positive sur l’épargne et tend à faire déprécier le taux de change réel d’équilibre.
). Une hausse de la productivité provoque à la fois une hausse de la production et de la consommation. Toutefois, puisque la propension marginale à consommer (β1) est inférieure à l’unité, l’effet sur l’offre domine, ce qui met une pression positive sur l’épargne et tend à faire déprécier le taux de change réel d’équilibre.
Le deuxième transite à travers l’investissement national ((1 –λ4)kα[γ4 + γ1αk–1]). D’une part, une hausse de la productivité globale élève la productivité marginale du capital et stimule l’investissement. Il faut donc une appréciation réelle d’équilibre pour rétablir l’égalité entre l’offre et la demande globale de biens et services. D’autre part, ce même choc sur u, en augmentant le revenu national, améliore les perspectives de débouchés pour les firmes locales. Nous observons une nouvelle fois une augmentation de l’investissement et une appréciation réelle d’équilibre. Néanmoins, il convient d’insister sur le fait que l’appréciation du change réel à moyen terme par le biais du canal de l’investissement ne tient que si le pays domestique n’importe pas massivement les biens d’équipement, c’est-à-dire si λ4 est petit. Dans le cas contraire, la hausse des investissements entraîne un boom des importations, une forte détérioration de la balance commerciale et finalement une dépréciation réelle d’équilibre pour rééquilibrer le marché des biens et services.
Au total, l’impact global est indéterminé et tout dépend encore une fois du paramètre λ4. À moyen terme, un choc positif sur la productivité globale des facteurs apprécie (déprécie) le taux de change réel si et seulement si ![]() , soit :
, soit :
2.2.3 Le stock de capital productif
Lorsque la mobilité internationale des capitaux est parfaite, l’effet total du stock de capital productif sur le taux de change réel d’équilibre est donné à moyen terme par :
Là encore, trois canaux de transmission doivent être distingués. D’abord, une hausse du stock de capital productif modifie l’épargne nationale à travers deux effets opposés. En premier lieu, la production domestique est stimulée, ce qui augmente l’épargne. En second lieu, le niveau plus élevé de richesse pousse les ménages à la consommation, ce qui réduit l’épargne. Traditionnellement, le NATREX postule un impact positif de k sur s, ce qui suppose implicitement que la condition suivante soit vérifiée[20] :
Ensuite, l’investissement est affecté également par deux effets opposés. D’une part, la hausse de k diminue la productivité marginale du capital, donc l’investissement. D’autre part, l’amélioration des anticipations sur l’activité économique domestique et les perspectives de débouchés encouragent les firmes locales à investir. Aussi, l’investissement diminue (augmente) suite à un choc positif sur le stock de capital si[21]![]() .
.
Enfin, nous ne devons pas oublier le canal externe. Si le pays domestique importe massivement son capital productif, alors la baisse de i induite par la hausse de k diminue les importations et améliore la balance commerciale. Si le paramètre λ4 est suffisamment fort, l’effet de la balance commerciale peut très bien dominer celui de l’épargne. Au total, nous avons les conditions suivantes :
et
2.2.4 La préférence pour le présent et les dépenses publiques
Une augmentation du taux de préférence pour le présent et des dépenses publiques entraîne une augmentation de la consommation nationale (privée plus publique). La hausse induite de l’absorption domestique aboutit à un déséquilibre sur le marché des biens et services en faveur de la demande. La demande extérieure nette doit donc s’ajuster à la baisse, c’est-à-dire il se produit une appréciation réelle qui conduit à une détérioration de la balance commerciale. Nous avons donc :
et
2.2.5 Le taux d’intérêt réel mondial
Une hausse du taux d’intérêt réel mondial accroît le coût de l’emprunt et décourage donc l’investissement. L’apparition d’un excès d’offre domestique nécessite une balance commerciale excédentaire, c’est-à-dire une dépréciation réelle, d’où :
Bien entendu, ce résultat ne tient que si λ4 < 1. Dans le cas où les investissements sont massivement importés, il est plus probable d’observer une appréciation réelle.
2.2.6 Les termes de l’échange
Les termes de l’échange exercent un impact sur la parité réelle d’équilibre similaire à celui de la demande étrangère. Ces deux variables sont modélisées de la même manière, c’est-à-dire à travers des effets positifs sur les exportations et l’investissement national, d’où : ![]() . Tout dépend donc de l’importance des investissements importés (le paramètre λ4), soit :
. Tout dépend donc de l’importance des investissements importés (le paramètre λ4), soit :
et
2.2.7 La dette extérieure
Une détérioration de la position extérieure (augmentation de la dette) du pays a un impact négatif sur la consommation par le biais de l’érosion de la richesse. Le pays doit donc dégager un surplus commercial obtenu grâce à une dépréciation réelle, soit :
2.3 Les effets induits via l’imparfaite mobilité des capitaux
L’hypothèse de l’imparfaite mobilité internationale des capitaux bouleverse la détermination de l’équilibre à moyen terme. Celle-ci a des effets sur le taux de change réel à travers les mouvements endogènes du taux d’intérêt réel. La conséquence fondamentale du contrôle des changes se manifeste à travers la relation d’équilibre de portefeuille. En effet, la mobilité imparfaite des capitaux va rendre le taux d’intérêt réel domestique endogène au nouveau taux de change réel d’équilibre. Le taux d’intérêt réel n’est plus égal au taux d’intérêt mondial, mais il est donné par ![]() . Désormais, ce dernier participe, conjointement avec le taux de change réel, au processus d’ajustement. Le rôle crucial du taux d’intérêt réel domestique va modifier sensiblement l’impact des déterminants fondamentaux sur le taux de change réel à moyen terme. À côté de l’effet direct présenté précédemment, un effet indirect se manifeste à travers le canal du contrôle des changes. En effet, un choc donné sur une variable exogène et la modification du change réel qui en découle va transformer le poids de la dette externe libellée en devises, le taux d’intérêt réel domestique et donc l’investissement. Ce mécanisme ajoute ainsi un effet rétroactif du change sur l’absorption domestique, amplifiant ou réduisant l’influence des fondamentaux sur le niveau du taux de change réel d’équilibre.
. Désormais, ce dernier participe, conjointement avec le taux de change réel, au processus d’ajustement. Le rôle crucial du taux d’intérêt réel domestique va modifier sensiblement l’impact des déterminants fondamentaux sur le taux de change réel à moyen terme. À côté de l’effet direct présenté précédemment, un effet indirect se manifeste à travers le canal du contrôle des changes. En effet, un choc donné sur une variable exogène et la modification du change réel qui en découle va transformer le poids de la dette externe libellée en devises, le taux d’intérêt réel domestique et donc l’investissement. Ce mécanisme ajoute ainsi un effet rétroactif du change sur l’absorption domestique, amplifiant ou réduisant l’influence des fondamentaux sur le niveau du taux de change réel d’équilibre.
L’introduction de l’imparfaite mobilité des capitaux peut être représentée graphiquement dans le plan (e, r). Nous devons tracer d’une part l’équilibre de portefeuille, noté Ep, qui donne une relation décroissante entre le taux de change réel et le taux d’intérêt réel :
Nous représentons d’autre part l’équilibre sur le marché des biens et services (EI) qui établit une relation entre le change réel et le taux d’intérêt réel dont le signe dépend du paramètre λ4 :
Finalement, deux cas doivent être distingués selon qu’il y ait initialement une appréciation ou une dépréciation réelle, c’est-à-dire selon l’importance des investissements importés (λ4). Pour présenter clairement les forces en action, nous prenons le cas d’un choc positif (négatif) sur la productivité globale. D’un côté, si λ4 est faible (graphique 1), la hausse (baisse) de u apprécie (déprécie) initialement le taux de change réel. La hausse (baisse) du taux d’intérêt réel domestique induite décourage (encourage) l’investissement et l’absorption nationale. Le taux de change réel d’équilibre doit alors se déprécier (s’apprécier) afin de dégager le surplus (déficit) commercial nécessaire au rétablissement de l’équilibre du marché des biens et services, ce qui atténue l’appréciation (la dépréciation) réelle initiale, c’est-à-dire à taux de change réel constant. D’un autre côté, si λ4 est fort (graphique 2), la hausse (baisse) de u déprécie (apprécie) initialement le taux de change réel. La baisse (hausse) induite du taux d’intérêt réel stimule (réduit) l’investissement et la demande. Il se produit alors un afflux (reflux) d’importations dégradant (améliorant) la balance commerciale et exigeant une nouvelle dépréciation (appréciation) réelle.
Pour conclure sur ce point, précisons que les résultats précédents sont généralisables à l’ensemble des facteurs fondamentaux. Lorsque les investissements sont massivement importés alors l’effet direct est renforcé par l’action de l’imparfaite mobilité des capitaux. Dans le cas contraire, celle-ci atténue l’ampleur de l’effet direct.
Graphique 1
L’effet de l’imparfaite mobilité des capitaux avec λ4 petit
Graphique 2
L’effet de l’imparfaite mobilité des capitaux avec λ4 grand
3. Le taux de change réel d’équilibre de long terme
La solution de long terme est obtenue lorsque l’économie a atteint son point d’équilibre stationnaire stable. À ce niveau, la dette extérieure et le capital productif se fixent à leur état stationnaire déterminé par les variables fondamentales. En conséquence, le taux de change réel d’équilibre est fonction uniquement de ses déterminants fondamentaux. En d’autres termes, l’équilibre de long terme est un équilibre de moyen terme, c’est-à-dire la réalisation conjointe de l’équilibre du marché des biens et services et de l’équilibre de portefeuille pour ė = 0, avec deux conditions supplémentaires, à savoir ḟ = 0 et k̇ = 0. De plus, par souci de simplification et de manière à présenter clairement le rôle de l’imparfaite mobilité des capitaux à long terme, le modèle est résolu, d’une part, dans le cas d’une parfaite mobilité des capitaux (θ ≈ 0), et, d’autre part, dans le cas d’une absence totale de mobilité des capitaux (θ ≈ ∞).
3.1 Équilibre de long terme et parfaite mobilité des capitaux
Dans cette configuration, le contrôle des changes n’existe pas et le paramètre θ est nul, c’est-à-dire le taux d’intérêt réel domestique est égal au taux d’intérêt réel mondial.
3.1.1 Une solution analytique
À long terme, il faut résoudre le système d’équations ( k̇ = ḟ = ė =0) en fixant le paramètre θ = 0 afin de déduire la solution unique et stable donnée par le triplet (k*, f*, e*). Toutefois, chaque équation de ce système peut être résolue séparément.
En premier lieu, le capital productif se déduit de k̇ = 0 et ė = 0. En annulant l’équation (11), nous avons :
D’où l’expression du capital productif à long terme (k*)[22] qui est fonction de la productivité globale des facteurs, des termes de l’échange, de la demande et du taux d’intérêt réel à l’étranger :
De plus, à l’état stationnaire, le stock de capital doit être stable. De par la formulation particulière de la fonction d’investissement, cette propriété n’est pas automatiquement garantie[23] et une condition doit être respectée, soit :
En second lieu, le niveau de long terme de la dette externe (f*) est donné pour ḟ = 0, c’est-à-dire la condition de soutenabilité de la dette externe à long terme[24], et ė = 0. En partant de l’équation (13), nous posons :
De plus, étant donné qu’à l’état stationnaire, l’investissement est nul, l’équilibre sur le marché des biens et services peut s’écrire comme y – c – ḡ = b. En substituant cette expression dans (26), nous déduisons :
Finalement, en substituant (24) dans (27), nous constatons qu’à long terme la dette devient également endogène et dépend de la productivité globale des facteurs, des termes de l’échange, de la préférence pour le présent, des dépenses publiques, de la demande et du taux d’intérêt réel à l’étranger :
Il s’agit maintenant de voir dans quelles conditions cet équilibre est stable. Nous devons tout d’abord exprimer de nouveau l’équation (13) en tenant compte du niveau d’équilibre de moyen terme du change réel donné par (17), toujours pour θ = 0. La dynamique de la dette extérieure pouvant se réécrire comme ![]() [25], la condition suivante s’impose :
[25], la condition suivante s’impose :
Celle-ci s’interprête facilement. Si la dette extérieure augmente, le service de la dette augmente aussi de rw, ce qui pousse encore la dette vers le haut. Pour compenser, cette hausse entraîne dans le même temps une baisse de la richesse de β2 et donc de la consommation. Ceci va provoquer une diminution des importations et par conséquent un rééquilibrage de la stabilité de la dynamique de la dette. Ainsi, pour que l’effet de proportion soit respecté, il faut que l’impact de la richesse sur la consommation soit supérieur au taux d’intérêt réel étranger.
En dernier lieu, le taux de change réel d’équilibre de long terme (e*) se déduit de l’équilibre du marché des biens et services pour les valeurs d’état stationnaire du capital productif et de la dette extérieure. Plus précisément, à l’équilibre de long terme, le taux de change réel doit dégager le solde commercial compatible avec le remboursement des intérêts sur la dette, d’où[26] :
avec
ou encore :
Par conséquent, à long terme, avec la convergence du capital productif et de la dette extérieure vers leur niveau d’état stationnaire, le taux de change réel ne dépend plus que de ses fondamentaux réels, à savoir la productivité globale des facteurs, les termes de l’échange, la préférence pour le présent, les dépenses publiques, la demande étrangère et le taux d’intérêt réel mondial.
3.1.2 L’impact de la demande étrangère
Pour mettre en évidence l’effet de long terme d’une modification de la demande étrangère (ou de toute autre variable exogène d’ailleurs) sur le taux de change réel d’équilibre, il convient de distinguer l’effet direct, c’est-à-dire l’influence directe de la demande étrangère, des effets indirects, c’est-à-dire l’influence de la demande étrangère à travers les mouvements endogènes du capital productif et de la dette extérieure. Une hausse de la demande étrangère augmente le capital productif mais a un impact ambigu sur la dette externe :
et
En effet, la hausse de k consécutive à celle de yw stimule d’une part la production, ce qui diminue la dette, et d’autre part la consommation, ce qui alourdit la dette. Pour des raisons qui ont déjà été exposées plus haut (voir section 2.2.3), le premier domine le second (– (1 – β1)Pmk* > β2), impliquant qu’un choc positif sur la demande étrangère réduit la dette à l’état stationnaire. Cette ambiguïté se retrouve dans la dérivée de l’expression du taux de change réel d’équilibre par rapport à yw :
Plusieurs effets peuvent être dégagés. D’abord, une hausse de yw exerce un impact positif sur la balance commerciale par le biais de l’accroissement des exportations nationales. Pour maintenir un solde commercial constant, il faut donc une appréciation réelle d’équilibre. Ensuite, la hausse de k augmente la production et l’épargne et par voie de conséquence pousse la dette à diminuer. Les paiements d’intérêts sur la dette sont donc moins élevés et la condition d’équilibre externe exige un solde commercial plus faible obtenu grâce à une appréciation réelle. Mais, cette même hausse de k encourage les dépenses de consommation, lesquelles vont accroître la dette et la charge d’intérêt, ce qui tend à faire déprécier le taux de change réel. Néanmoins, si nous supposons que la dette finit par baisser à l’état stationnaire, cette indétermination disparaît. Aussi, le taux de change réel d’équilibre s’apprécie suite à une amélioration de la demande étrangère, d’où ![]() .
.
3.1.3 L’impact de la productivité globale des facteurs
Une amélioration de la productivité globale des facteurs modifie positivement le capital productif et négativement la dette extérieure, soit :
et
Même si le signe de la dérivée de la fonction de la dette par rapport à u n’est pas évident a priori, il est attendu qu’il soit négatif. Effectivement, bien que la hausse de la consommation suite à celle de k creuse la dette, le double effet de u sur la production (un effet pur et un effet par le biais de k) tend à la réduire fortement.
Par conséquent, si la dette externe diminue à long terme, un choc de productivité positif conduit à une appréciation réelle d’équilibre :
L’explication est la suivante. Une hausse de u entraîne un augmentation de la production et une accumulation de capital productif. Le stock de capital plus élevé engendre ensuite une nouvelle augmentation de la production mais également une plus forte consommation. Si le double effet sur la production supplante l’effet sur la consommation, la hausse subséquente de l’épargne nationale réduit la dette extérieure. L’économie domestique doit désormais dégager une balance commerciale compatible avec un niveau plus faible du service de la dette. Celle-ci est obtenue grâce à une appréciation du taux de change réel d’équilibre.
Cependant, le niveau de production plus élevé implique une demande d’importations plus grande, d’où une détérioration de la balance commerciale et une nécessaire dépréciation réelle d’équilibre pour un niveau constant de remboursement d’intérêts. Étant donné que, par hypothèse, le pays n’importe pas massivement les biens de consommation (λ3 faible), ce dernier effet est négligeable et ne remet pas en cause le résultat précédent, c’est-à-dire ![]() .
.
3.1.4 La préférence pour le présent
Un choc positif sur la préférence pour le présent n’a pas d’impact sur le capital mais accroît la dette extérieure d’équilibre :
et
La hausse de la dette engendre deux effets complémentaires. D’une part, la baisse de la richesse décourage la consommation et exerce une pression positive sur le change réel. D’autre part, le niveau plus fort de la dette à long terme entraîne une augmentation des paiements d’intérêts. La balance commerciale doit s’améliorer à travers une dépréciation réelle. Par conséquent, un choc positif sur le taux de préférence pour le présent est susceptible d’aboutir à une dépréciation réelle à long terme, d’où :
3.1.5 Les dépenses publiques
Un choc positif sur les dépenses publiques exerce le même type d’impact que la préférence pour le présent, à savoir un stock de capital inchangé et une dette plus importante à l’état stationnaire :
et
La richesse moindre et les flux de paiements d’intérêts plus élevés conduisent à une dépréciation réelle, soit :
Toutefois, la dépréciation réelle ne se produit que si ![]() , c’est-à-dire si λ3 est petit. En d’autres termes, l’effet indirect des dépenses publiques par le biais de la consommation, provoquant une amélioration de la balance commerciale, ne doit pas dominer l’effet direct sur la demande domestique.
, c’est-à-dire si λ3 est petit. En d’autres termes, l’effet indirect des dépenses publiques par le biais de la consommation, provoquant une amélioration de la balance commerciale, ne doit pas dominer l’effet direct sur la demande domestique.
3.1.6 Les termes de l’échange
L’impact des termes de l’échange s’analyse comme celui de la demande étrangère. Une hausse des termes de l’échange accroît le capital productif mais a un effet indéterminé sur la dette externe :
et
Néanmoins, puisque l’effet richesse est, par hypothèse, dominé par l’effet production, c’est-à-dire β2 < (1 – β1)Pmk*, la dette extérieure est plus susceptible de diminuer. Cette ambiguïté se retrouve dans l’expression de l’impact total sur le taux de change réel d’équilibre :
Trois effets peuvent être distingués suite à une hausse des termes de l’échange. Premièrement, les exportations sont stimulées, la balance commerciale s’améliore et le change réel s’apprécie pour maintenir l’équilibre externe. Les deux derniers opèrent à travers la hausse du capital productif. D’un côté, la production et l’épargne privée augmentent, ce qui fait diminuer la dette. La baisse des intérêts dûs à l’étranger nécessite une détérioration de la balance commerciale et une appréciation réelle. De l’autre, la consommation s’élève par le biais de la richesse, augmentant la dette et dépréciant le change réel. Au final, conformément aux résultats empiriques (Hoarau, 2006; Rey, 2009), il est légitime de supposer que cette dérivée est négative. Un choc positif sur les termes de l’échange aboutit à une appréciation réelle à long terme, d’où ![]() .
.
3.1.7 Le taux d’intérêt réel mondial
Nous analysons l’impact d’une hausse du taux d’intérêt réel mondial dans le cas d’une économie débitrice vis-à-vis du reste du monde (f > 0) par hypothèse. Au préalable, ce choc entraîne une chute du capital productif et une accumulation de dette extérieure :
et
De son côté, le taux de change réel d’équilibre va se déprécier pour deux raisons. Tout d’abord, pour une position débitrice donnée, une hausse du taux d’intérêt réel mondial alourdit la charge des paiements d’intérêts. La balance commerciale doit donc s’améliorer par le biais d’une dépréciation réelle. Ensuite, la hausse du niveau de long terme de la dette extérieure, induite par rw et k, provoque un accroissement des flux d’intérêts versés. Il faut ainsi une nouvelle dépréciation réelle et une amélioration du solde commercial pour respecter l’équilibre externe. L’impact total pour λ3 faible est donc donné par :
3.2 Équilibre de long terme et absence de mobilité des capitaux
Nous montrons plus avant que lorsque la mobilité des capitaux est nulle, le taux de change réel n’influence pas l’équilibre du marché des biens et services. Son rôle n’est plus que de maintenir continuellement une balance commerciale équilibrée.
3.2.1 Une solution analytique
Dans le cas de l’absence totale de mobilité des capitaux (θ = +∞), de nouvelles conditions doivent être prises en compte. Tout d’abord, l’endettement externe est nul, ce qui signifie que f = 0. Ensuite, le taux d’intérêt réel étranger est supposé n’exercer aucun effet sur l’économie domestique. Ces hypothèses sont cruciales pour la détermination de l’équilibre de long terme du modèle qui se résume désormais par le couple (k*, e*).
Dans un premier temps, le niveau du capital productif à long terme se déduit de l’équilibre du marché des biens et services pour k̇ = f = b = 0, soit :
En résolvant pour k*, il vient :
Par conséquent, le capital productif à l’état stationnaire est fonction de la productivité globale des facteurs, des dépenses publiques et de la préférence pour le présent. De plus, en substituant (33) dans l’équation k̇ = 0, il est possible de trouver l’expression du taux d’intérêt réel d’équilibre à l’état stationnaire (r*), c’est-à-dire :
Enfin, à l’état stationnaire, la dynamique du capital productif doit être stable. Puisque dans le cas où θ = +∞, la dette extérieure et par voie de conséquence la balance commerciale sont toutes deux nulles, nous avons ![]() , d’où :
, d’où :
Ainsi, une fois de plus, l’effet richesse occupe une place importante dans notre analyse. En effet, β2 doit être grand pour que le capital productif soit stable à long terme.
Dans un second temps, étant donné que la dette extérieure du pays est supposée nulle, le rôle du taux de change réel à long terme, dans ce cas de figure, est de maintenir continuellement la balance commerciale équilibrée. Il se déduit par conséquent de ḟ = f = b=0.
En posant l’équilibre sur le marché des biens et services y = c + ḡ et résolvant pour e*, il découle :
avec ![]()
d’où :
Par conséquent, à l’exception du taux d’intérêt réel étranger, l’ensemble des fondamentaux n’est pas modifié par rapport au cas de parfaite mobilité des capitaux. Toutefois, puisque le rôle du change réel a changé, c’est-à-dire qu’il n’influence plus l’équilibre du marché des biens et services, les effets exercés par les fondamentaux doivent eux aussi être différents.
3.2.2 L’impact de la demande étrangère
Lorsque la mobilité des capitaux est totalement absente, l’ambiguïté des résultats concernant l’influence des fondamentaux à long terme disparaît. L’effet de la demande étrangère découle de la dérivée de (37) par rapport à yw, à savoir :
avec ![]() .
.
Étant donné que la demande étrangère n’a pas d’impact sur le capital productif à l’état stationnaire, seul l’effet direct est présent (λ2). Ainsi, un choc positif sur la demande étrangère stimule les exportations nationales et améliore la balance commerciale. Puisque cette dernière doit être constamment égale à zéro, le taux de change réel d’équilibre s’apprécie.
3.2.3 L’impact de la productivité globale des facteurs
En ce qui concerne l’impact de la productivité globale, les résultats sont tout aussi clairs. En effet, nous montrons que sous l’hypothèse d’un effet richesse fort à long terme, ce qui est nécessaire pour vérifier la stabilité du capital productif, l’effet indirect à travers k* renforce l’effet direct, impliquant une dépréciation réelle d’équilibre.
La dérivée de l’équation (37) par rapport à u donne :
avec ![]() .
.
Le mécanisme est le suivant. Une hausse de la productivité globale provoque une augmentation de la production domestique, ce qui engendre un excès d’offre sur le marché des biens et services. Comme à long terme l’effet richesse est dominant, l’équilibre sur ce marché ne peut être obtenu que par une augmentation du capital productif. Cette dernière stimule la richesse. Le surcroît de consommation qui en découle aboutit à un gonflement des importations et à une détérioration de la balance commerciale. Par conséquent, pour que l’équilibre externe tienne, c’est-à-dire une balance commerciale nulle, le taux de change réel d’équilibre doit se déprécier.
3.2.4 La préférence pour le présent et les dépenses publiques
Une hausse de la préférence pour le présent et des dépenses publiques met une pression positive sur la consommation. L’excès de demande qui en résulte nécessite une baisse du capital productif pour garantir l’équilibre sur le marché des biens et services (avec un effet richesse fort), soit :
et
La baisse du capital productif réduit la richesse, la consommation et la demande d’importations émanant des résidents[27]. L’objectif d’une balance commerciale nulle nécessite donc une appréciation réelle d’équilibre, soit :
et
3.2.5 Les termes de l’échange
Une amélioration des termes de l’échange n’exerce aucun impact sur le capital productif, soit :
Par conséquent, l’effet des termes de l’échange sur le taux de change réel se résume par l’effet direct sur la balance commerciale. Un choc positif sur les termes de l’échange stimule les exportations nationales, ce qui est bénéfique pour la balance commerciale. Il faut alors une appréciation réelle pour ramener celle-ci à sa cible, d’où :
4. La dynamique du taux de change réel d’équilibre
Auparavant, les solutions statiques de moyen et de long terme ont été mises en évidence. Il convient maintenant d’étudier de manière plus explicite la dynamique de transition qui permet le passage de l’équilibre de moyen terme à celui de long terme. L’approche stock-flux de type NATREX que nous présentons délivre une avancée certaine au niveau de l’aspect dynamique du change réel d’équilibre. En effet, en prenant en compte les ajustements de moyen à long terme des variables prédéterminées, elle montre que la parité réelle d’équilibre doit être définie comme une trajectoire plutôt que comme un point d’ancrage fixe.
4.1 La construction du système dynamique
Avant d’exposer la solution dynamique du modèle, deux remarques doivent être précisées. D’abord, afin d’isoler de manière simple les forces en présence dans le processus d’ajustement, notre présentation repose sur des fonctions et des solutions d’équilibre prises sous leur forme générale. Ensuite, nous nous plaçons dans la situation intermédiaire d’une imparfaite mobilité des capitaux (θ > 0).
Si z est une variable regroupant l’ensemble des fondamentaux du modèle, le taux de change réel à moyen terme peut s’écrire sous sa forme la plus simple :
Si nous prenons la différentielle totale de (38) par rapport au temps, nous obtenons :
La description du système dynamique complet nécessite donc l’explicitation d’un sentier d’ajustement équilibré pour le stock de capital et la dette extérieure.
La dynamique du capital productif est donnée par :
De même, la trajectoire de la dette extérieure s’écrit :
À partir de là, il est possible de définir les deux relations dynamiques d’équilibre qui vont permettre de déduire les niveaux d’état stationnaire du capital et de la dette.
Cette relation représente toutes les combinaisons du capital et de la dette pour lesquelles le taux d’investissement net est égal à zéro. Sur le graphique (3), la droite représentant k̇ = 0 est de pente négative[28]. En effet, d’une part, la condition d’imparfaite mobilité des capitaux fait que la hausse de f augmente le taux d’intérêt réel domestique et décourage donc l’investissement. D’autre part, une hausse de k agit négativement sur l’investissement par le biais de la productivité marginale mais positivement grâce aux anticipations de demande. Néanmoins, il a été démontré que la stabilité du capital productif exige que l’effet productivité domine l’effet demande[29]. Nous posons par conséquent une relation inverse entre le stock de capital et l’investissement. À gauche de k̇ = 0, le taux d’investissemeent est positif, ce qui fait augmenter k. À droite, le taux d’investissement devient négatif et k diminue[30].
Graphique 3
La dynamique du capital productif
Une équation similaire peut être écrite pour la dynamique de la dette extérieure :
Cette relation indique l’ensemble des combinaisons du capital et de la dette extérieure pour lesquelles les flux de capitaux (et donc le compte courant) sont nuls. La droite représentant ḟ = 0, donnée par le graphique 4, est aussi de pente négative. En effet, une hausse de f entraîne une hausse de l’épargne par rapport à l’investissement. Cette dernière augmente car la consommation baisse par le biais de l’impact négatif de f sur la richesse. L’investissement baisse avec l’augmentation du taux d’intérêt réel. De plus, une hausse de k décourage l’investissement et réduit donc la dette. Par conséquent, à gauche de ḟ = 0, il y a des déficits de compte courant, c’est-à-dire des flux d’entrée nets de capitaux, ce qui fait augmenter f. À droite de ḟ = 0, c’est la situation inverse avec des excédents de compte courant et une diminution de la dette extérieure.
Graphique 4
La dynamique de la dette extérieure
La solution dynamique complète est réalisée par la construction du diagramme des phases (5) donné par la juxtaposition des deux conditions d’équilibre (42) et (43).
La solution stationnaire de long terme, c’est-à-dire le couple (k*, f*), est donc le point d’intersection (le point P du graphique 5) des deux droites d’équation k̇ = 0 et ḟ = 0 tel que :
La résolution de ce système donne le niveau d’état stationnaire du capital et de la dette, à savoir k* et f*, en fonction des fondamentaux z :
Ainsi, à long terme, le capital et la dette deviennent des fonctions des fondamentaux et par conséquent le taux de change réel d’équilibre à l’état stationnaire n’est plus déterminé que par les seules variables fondamentales :
Graphique 5
Représentation graphique de l’équilibre dynamique
Par ailleurs, le graphique 5 montre que cet équilibre est stable. En effet, quel que soit le point de départ, le système finit toujours par converger vers le point stationnaire P. Toutefois, cette stabilité n’est pas un fait établi et plusieurs conditions doivent être remplies. Pour les mettre en évidence, nous posons la matrice jacobienne représentant la dynamique des variables prédéterminées au voisinage de l’équilibre stationnaire, soit :
Pour que le système soit stable, il faut que le déterminant et la trace de Mj soient respectivement positif et négative :
et
D’après les conditions de stabilité du capital et de la dette, la trace est toujours négative. Par contre, pour que le déterminant soit positif, il faut que ![]() . En d’autres termes, la pente de ḟ = 0 doit être supérieure à celle de k̇ = 0.
. En d’autres termes, la pente de ḟ = 0 doit être supérieure à celle de k̇ = 0.
4.2 L’analyse dynamique de différents chocs
Cette représentation simplifiée ne doit pas masquer la présence à la fois d’effets directs et indirects. La différentielle totale de (46) par rapport à z donne :
Le terme entre crochets représente les effets indirects (de long terme), par le biais du processus d’évolution du stock de capital et de la dette extérieure, et le terme restant l’effet direct (de moyen terme). Pour bien comprendre l’imbrication de ces différents effets, il convient d’analyser deux cas d’école montrant l’influence des fondamentaux à différentes étapes du processus d’évolution de l’économie : un choc de demande et un choc d’offre.
4.2.1 Un choc du côté demande
Si la consommation globale augmente, par exemple suite à une hausse du taux de préférence pour le présent (ρ) ou des dépenses publiques (ḡ), l’épargne domestique va baisser par rapport à l’investissement. Ainsi, au niveau national, l’épargne ne suffira pas à financer l’investissement, c’est-à-dire qu’il y a un excès de demande. La restauration de l’équilibre interne nécessite soit une appréciation réelle à taux d’intérêt réel constant, soit un accroissement du taux d’intérêt réel à taux de change réel constant. En fait, puisque la mobilité internationale du capital est imparfaite, ces deux ajustements se produisent simultanément. La hausse du taux d’intérêt réel incite les investisseurs étrangers à demander des titres nationaux, ce qui amène donc des flux d’entrée nets de capitaux. Par conséquent, l’effet direct de z est d’apprécier le taux de change réel d’équilibre ![]() , conduisant à des déficits de compte courant.
, conduisant à des déficits de compte courant.
Nous devons aussi considérer les effets indirects. Les déficits de compte courant augmentent la dette, ce qui décourage la formation de capital par le biais de la hausse du taux d’intérêt réel. Ceci nous donne l’effet de z sur k et f à savoir ![]() et
et ![]() . Au fur et à mesure que la dette augmente, la consommation diminue à l’instar de l’épargne jusqu’à ce que l’équilibre épargne-investissement soit rétabli. Sur le diagramme de phases (5), ceci correspond à la trajectoire [KP].
. Au fur et à mesure que la dette augmente, la consommation diminue à l’instar de l’épargne jusqu’à ce que l’équilibre épargne-investissement soit rétabli. Sur le diagramme de phases (5), ceci correspond à la trajectoire [KP].
À mesure que l’épargne augmente, sous la pression de l’effet richesse positif exercé par le capital et la dette, les capitaux sortent, le taux de change réel se déprécie et le compte courant se redresse, d’où ![]() et
et ![]() . Toutefois, la dette se stabilise à un niveau plus fort que le niveau initial. Le taux de change réel doit donc se déprécier une nouvelle fois pour dégager le surplus de la balance commerciale nécessaire pour servir les paiements d’intérêt sur la dette[31]. Sous l’impulsion de la dette extérieure, le taux de change réel se surdéprécie, ce qui compense même l’appréciation de moyen terme.
. Toutefois, la dette se stabilise à un niveau plus fort que le niveau initial. Le taux de change réel doit donc se déprécier une nouvelle fois pour dégager le surplus de la balance commerciale nécessaire pour servir les paiements d’intérêt sur la dette[31]. Sous l’impulsion de la dette extérieure, le taux de change réel se surdéprécie, ce qui compense même l’appréciation de moyen terme.
4.2.2 Un choc du côté offre
Dans le cas d’un choc d’offre, par exemple suite à une hausse de la productivité globale[32] (u), l’investissement augmente et finit par supplanter l’épargne. L’effet direct des fondamentaux est le même que précédemment, c’est-à-dire une appréciation réelle du change ![]() , des flux d’entrée nets de capitaux et un déficit de compte courant. Par conséquent, la dette et le capital progressent ensemble. Cela correspond sur le graphique 5 à la trajectoire [BH].
, des flux d’entrée nets de capitaux et un déficit de compte courant. Par conséquent, la dette et le capital progressent ensemble. Cela correspond sur le graphique 5 à la trajectoire [BH].
Toutefois, la hausse du stock de capital va déprimer l’investissement[33] et va stimuler l’épargne par la hausse de la production. L’économie finit par dégager des surplus de compte courant, ce qui entraîne des flux de sortie nets de capitaux. La dette commence alors à diminuer et elle se stabilise à un niveau inférieur au niveau initial. Le capital continue à augmenter vers son niveau d’état stationnaire fixé par les fondamentaux. C’est la trajectoire [HP] du graphique 5. L’effet de z sur k et f se résume donc respectivement par ![]() et
et ![]() .
.
La baisse de la dette réduit les paiements d’intérêts et par la conditon d’équilibre externe, le taux de change réel doit s’apprécier, d’où ![]() . La hausse du stock de capital provoque une hausse de la production et de la demande d’importations, ce qui dégrade la balance commerciale et pousse le change réel à se déprécier
. La hausse du stock de capital provoque une hausse de la production et de la demande d’importations, ce qui dégrade la balance commerciale et pousse le change réel à se déprécier ![]() . Puisque l’impact de la consommation sur la balance commerciale est supposé faible, le premier effet l’emporte et le taux de change réel finit par s’apprécier.
. Puisque l’impact de la consommation sur la balance commerciale est supposé faible, le premier effet l’emporte et le taux de change réel finit par s’apprécier.
Conclusion
En résumé, la théorie NATREX fournit un cadre conceptuel intéressant dans lequel le taux de change réel d’équilibre pour une petite économie développée est déterminé par un ensemble de fondamentaux constitué de la préférence pour le présent, de la productivité globale, des termes de l’échange, des dépenses publiques, du taux d’intérêt réel mondial et de la demande étrangère. Celle-ci montre clairement que le taux de change réel d’équilibre dépend de l’horizon temporel retenu. À moyen terme, il est déterminé dans le cadre d’un équilibre de flux. La parité d’équilibre est donc fonction des fondamentaux et des variables prédéterminées que sont la dette extérieure et le capital productif. À long terme, par contre, des ajustements de nature stock-flux, liés aux mouvements endogènes de la dette extérieure et du capital productif sont explicitement incorporés. La parité d’équilibre ne dépend plus alors que des seuls fondamentaux réels. Cette distinction entre équilibre de moyen terme et équilibre de long terme est un atout incontestable par rapport aux approches concurrentes. Un autre avantage du NATREX est qu’il propose une théorie explicative des flux de capitaux structurels. L’épargne nationale est modélisée selon la théorie du revenu permanent alors que l’investissement national se déduit du q de Tobin.
De plus, notre formulation du NATREX a permis de faire ressortir l’importance cruciale de certains paramètres structurels du modèle, à savoir l’effet richesse à long terme, le degré de dépendance de l’économie domestique vis-à-vis de l’extérieur en matière d’investissements importés à moyen terme et l’imparfaite mobilité des capitaux au niveau international. Cette dernière a des conséquences importantes sur la détermination de l’équilibre à la fois à moyen et à long terme. La principale modification associée à l’imparfaite mobilité des capitaux est d’introduire, à côté du taux de change réel, une autre variable d’ajustement, en l’occurrence le taux d’intérêt réel qui n’est plus fixé par le niveau mondial. Selon les cas, l’effet initial des fondamentaux réels (avec parfaite mobilité des capitaux) s’en trouve renforcé ou contrebalancé. En corollaire, la richesse structurelle du modèle lui permet de reproduire les spécifités d’une économie donnée et apporte une réponse adaptée au problème d’hétérogénéité qui prévaut même parmi le groupe des pays avancés.
Enfin, notre travail a également un intérêt certain en termes de politique économique. Le contexte actuel de crise qui sévit en Europe a révélé l’urgence de mener des réflexions approfondies sur l’élaboration d’une nouvelle théorie des crises financières. La prise en compte des interactions entre le taux de change réel d’équilibre et la dette externe dans le cadre de notre approche offre une perspective intéressante dans ce domaine. Stein (2006) montre notamment qu’il est possible de définir des signaux d’alerte pour les pays qui connaissent des difficultés financières en combinant un modèle NATREX « sur mesure » et le modèle de dette optimale. Nous observons parmi ces indicateurs celui de l’écart entre le taux de change réel effectif et sa valeur d’équilibre donnée par le NATREX de long terme. Une surévaluation de la monnaie nationale par rapport à cette référence constitue un signal fort de risque de crise monétaire[34]. Aussi, pour identifier et limiter les retombées négatives de ce type de distorsions, les décideurs de politique économique ont besoin de comprendre avec précision (selon le type d’économie considérée) comment se déterminent les taux de change à long terme.
Appendices
Notes
-
[1]
La littérature identifie au moins quatre coûts majeurs associés au mésalignement réel (Stemitsiotis, 1992) : (i) les crises de change; (ii) des phénomènes de désindustrialisation, l’explosion du chômage et une croissance économique faible sur le moyen et long terme; (iii) des pressions inflationnistes en cas d’alternance de périodes de surévaluation et de sous-évaluation et (iv) des pressions protectionnistes durables.
-
[2]
Dans la version absolue, le taux de change nominal est déterminé par le rapport entre les niveaux de prix entre deux pays. Le niveau d’équilibre du taux de change réel se déduit alors facilement de cette relation puisqu’il est finalement égal à l’unité. Dans la version relative, le taux de change nominal évolue de manière à effacer les écarts d’inflation entre pays. Le taux de change réel est donc constant et n’est plus forcément unitaire.
-
[3]
Dans ce cas de figure, le taux de change réel est côté à l’incertain. Son augmentation, obtenue par une hausse du taux de change nominal (E) et/ou une baisse du prix relatif des biens nationaux
 , est synonyme d’amélioration de la compétitivité-prix du pays considéré.
, est synonyme d’amélioration de la compétitivité-prix du pays considéré. -
[4]
Sur le plan empirique, un avantage manifeste en termes de fort pouvoir explicatif se dégage des différentes études. Ces dernières se sont orientées vers deux directions méthodologiques : (i) l’estimation d’une forme réduite simple se rapportant uniquement au taux de change réel (Crouhy-Veyrac et Saint-Marc, 1995; Lim et Stein, 1995; Song, 1997; Duval, 2001; Hoarau, 2006; Rey, 2009; You et Sarantis, 2012) et (ii) l’introduction d’une structure dans l’estimation (Gandolfo et Felettigh, 1998; Detken et al., 2002; Belloc et Federici, 2010).
-
[5]
En ce qui concerne les termes de l’échange, c’est généralement l’observation empirique qui établit s’ils sont endogènes ou exogènes. Une explication intéressante est fournie par Allen (1995).
-
[6]
Certains travaux introduisent aussi dans cette configuration la distinction entre biens échangés et non échangés.
-
[7]
Pour ne pas alourdir la présentation, les fondements microéconomiques des équations structurelles (consommation, investissement,...) ne sont que sommairement abordés. Précisons simplement que le NATREX fait appel aux techniques de programmation dynamique et de contrôle optimal stochastique en environnement incertain (Stein et Paladino, 2001; Stein, 2006).
-
[8]
Cette fonction de production traditionnelle suppose l’utilisation de deux facteurs, à savoir le travail et le capital. Il est possible d’introduire également le facteur « ressource naturelle ». Song (1997), en incorporant dans la fonction de production, à côté du travail et du capital, une matière première importée dans le cas du Japon, montre que celle-ci, bien qu’affectant l’investissement, ne modifie pas qualitativement les résultats. Pour faciliter la présentation analytique, nous nous limitons par conséquent à une fonction simple.
-
[9]
Certains modèles préfèrent considérer un taux d’épargne exogène (s*) tel que ρ = –s* (Stein, 1995; Stein, 1999).
-
[10]
Nous supposons que les consommateurs privés considèrent leur revenu sur la base du PIB plutôt que du PNB. Cela permet d’évacuer une source de complexité liée au terme des paiements d’intérêts sur la dette.
-
[11]
Nous montrons par la suite que cet « effet richesse », conformément à la tradition des modèles NATREX, occupe une place déterminante dans notre approche, notamment dans le mécanisme de stabilisation de la dette extérieure. Il constitue également une des principales limites des approches NATREX. En effet, le fait de stipuler que la fonction de consommation globale des ménages intègre un tel effet richesse implique que les agents privés de l’économie domestique incorporent dans leur comportement de consommation la position extérieure nette de la nation, ce qui est rarement le cas dans la réalité. Stein (1995) reconnait lui-même ce défaut et indique que ce mécanisme tient encore si la position extérieure nette constitue une variable explicative du comportement budgétaire de l’État.
-
[12]
La formulation de la contrainte budgétaire de l’État est très réductrice. En effet, elle évacue d’emblée les sources de financement hors impôt et la dimension intertemporelle. Toutefois, puisque le modèle est écrit en termes réels et qu’il se place directement dans une optique de moyen-long terme, cette simplification ne pose pas de problème majeur.
-
[13]
Pour formaliser la relation existant entre l’investissement et la situation sur les marchés boursiers, Tobin définit le coefficient q comme le rapport entre la valeur boursière de la firme et sa valeur comptable, c’est-à-dire la valeur de remplacement du capital. Ensuite, l’investissement est traité comme une fonction positive de q. Si q est inférieur à l’unité, le capital nouveau coûte trop cher par rapport à la valorisation boursière du capital existant. Il est donc préférable d’acheter une entreprise sur le marché plutôt que d’investir. Si, au contraire, q est supérieur à l’unité, il devient rentable d’investir, puisque les anticipations de profit incorporées dans les cours boursiers dépassent le coût d’achat du capital.
-
[14]
Nous faisons l’hypothèse que le pays produit un bien qui est consommé et exporté au même prix Px.
-
[15]
Le taux de change réel peut aussi influencer le coefficient q. Néanmoins, sa prise en compte ne bouleverse pas les résultats d’ensemble (Duval, 2001).
-
[16]
Cf. note de bas de page 3.
-
[17]
Plus précisément, trois cas apparaissent selon l’hypothèse faite à l’égard du contrôle des changes :
Si on admet l’hypothèse forte de parfaite mobilité des capitaux (θ = 0), alors le terme
 est nul. On retrouve l’égalité des taux d’intérêt national et étranger. Ainsi, tout changement de i ou de s (et donc du solde de la balance des capitaux) se traduit uniquement par une modification du taux de change réel, laquelle permet un ajustement de la balance courante.
est nul. On retrouve l’égalité des taux d’intérêt national et étranger. Ainsi, tout changement de i ou de s (et donc du solde de la balance des capitaux) se traduit uniquement par une modification du taux de change réel, laquelle permet un ajustement de la balance courante. Si on retient l’hypothèse contraire, c’est-à-dire celle de l’absence totale de mobilité des capitaux (θ = +∞), le terme
 est très grand. Le taux d’intérêt réel devient la seule variable d’ajustement et se modifie afin de garantir l’égalité. Par conséquent, tout changement de i ou de s produit l’ajustement nécessaire du taux d’intérêt réel domestique (r) qui n’affecte ni le taux de change réel ni le compte courant.
est très grand. Le taux d’intérêt réel devient la seule variable d’ajustement et se modifie afin de garantir l’égalité. Par conséquent, tout changement de i ou de s produit l’ajustement nécessaire du taux d’intérêt réel domestique (r) qui n’affecte ni le taux de change réel ni le compte courant. Si on se place enfin dans une situation intermédiaire, c’est-à-dire celle d’imparfaite mobilité des capitaux (0 < θ < +∞), il y a alors deux variables d’ajustement puisque les changements de l’écart s – i influencent directement à la fois le taux de change réel et le taux d’intérêt réel domestique.
-
[18]
La non-modélisation du court terme fait que le NATREX n’échappe pas à la contrainte de l’effet d’hystérèse, c’est-à-dire la dynamique du taux de change réel n’est pas neutre sur son niveau d’équilibre de long terme. Tout dépend alors de la vitesse de convergence du taux de change réel de court terme vers le NATREX de moyen terme. S’il existe dans l’économie des mécanismes forts de rigidité nominale sur le change et les prix intérieurs, ce problème ne peut être négligé (Hinkle et Montiel, 1999).
-
[19]
Hoarau et al. (2003) montrent plus précisément que l’effet de la demande étrangère sur la balance commerciale prend la forme d’une courbe en J. En effet, suite à une hausse de yw, le pays doit importer le capital productif nécessaire pour répondre à ce surcroît de demande. Par conséquent, la balance commerciale se détériore dans un premier temps. Lorsque le pays a accumulé suffisamment de capital, il peut alors satisfaire la demande étrangère par une hausse des exportations. La balance commerciale va donc, dans un second temps, s’améliorer.
-
[20]
Ceci indique donc que l’effet production domine l’effet dépense (ou encore l’effet richesse). Cette hypothèse aura des conséquences importantes pour l’équilibre de long terme (voir section 3.1).
-
[21]
Nous montrons plus loin que cette condition doit être respectée pour vérifier la stabilité du stock de capital. Pour le moment, nous nous contentons de l’admettre.
-
[22]
De par la spécification de la fonction d’investissement, il est difficile de trouver une forme explicite pour le capital productif à l’état stationnaire, ce qui nous incite à donner simplement sa forme réduite. Néanmoins, cela ne limite pas notre analyse puisque seules les dérivées partielles sont indispensables.
-
[23]
L’investissement ne décroît pas automatiquement avec une hausse du capital productif.
-
[24]
Cette condition découle de la contrainte budgétaire intertemporelle de la nation, prise dans sa version la moins restrictive (Burda et Wyploz, 1998). En effet, la contrainte budgétaire intertemporelle de la nation ordinaire stipule que tout ce qu’un pays doit aujourd’hui (court terme) doit être entièrement remboursé demain (long terme). Or, dans notre modèle, nous supposons simplement que la dette doit se stabiliser à long terme à un niveau qui soit soutenable, c’est-à-dire qu’elle ne doit pas exploser.
-
[25]
Les éléments non pertinents ont été écartés de la relation.
-
[26]
Dans la suite de l’article, le dénominateur de la relation (30) est noté l.
-
[27]
Dans le cas des dépenses publiques, les importations diminuent également par la chute du revenu disponible des ménages qui découle des impôts supplémentaires.
-
[28]
En cas de parfaite mobilité des capitaux, cette droite serait indépendante de f et par conséquent parallèle à l’axe des ordonnées.
-
[29]
Nous nous plaçons d’emblée sur la partie de la fonction d’investissement décroissante en k.
-
[30]
Sur le graphique, la direction du champ de vecteurs est matérialisée par des flèches.
-
[31]
Néanmoins, la hausse de la dette et la baisse induite de la consommation provoquent un redressement de la balance commerciale par la chute des importations, d’où une tendance à l’appréciation réelle. Nous ne considérons pas cet effet et le supposons négligeable.
-
[32]
La demande mondiale (yw), les termes de l’échange (T) et le taux d’intérêt réel mondial (rw) exercent le même type d’influence que la productivité globale. Aussi, nous ne les développons pas. Néanmoins, il est important de préciser que pour le taux d’intérêt réel mondial, il faut considérer le cas d’un choc d’offre négatif.
-
[33]
La baisse de la productivité marginale et la hausse du taux d’intérêt réel dominent l’amélioration des anticipations de demande.
-
[34]
Stein (2006) propose également un deuxième indicateur qui complète le premier, à savoir l’écart entre la dette effective et la dette optimale. Si la première dépasse la seconde, alors le pays court le risque de faire défaut dans la mesure où il devra diminuer sa consommation pour faire face au service de la dette.
Bibliographie
- Agenor, P.R. (2000), The Economics of Adjustment and Growth, The World Bank, Washington, D.C.
- Allen, P. R. (1995), « The Economic and Policy Implications of the NATREX Approach », in Stein, J. L., P. R. Allenet alii, Fundamental Determinants of Exchange Rates, Oxford Clarendon Press, p. 1-37.
- Artus, P. (1998), « Le taux de change réel d’équilibre : un modèle général », Document de travail de la caisse des dépôts et consignations, janvier, no 1998-17/EI.
- Asea, P. et E. Mendoza (1994), « The Balassa-Samuelson model : A General Equilibrium Appraisal », Review of International Economics, 2(3) : 244-267.
- Balassa, B. (1964), « The Purchasing Power Parity Doctrine : A Reappraisal », Journal of Political Economy, 72 : 584-596.
- Balvers, R. J. et J. H. Bergstrand (2002), « Government Expenditure and Equilibrium Real Exchange Rates », Journal of International Money and Finance, 21 : 667-692.
- Bayoumi, T., P. Clark, S. Symansky et M. Taylor (1994), « The Robustness of Equilibrium Exchange Rate Calculations to Alternative Assumptions and Methodologies », in Williamson J. (éd.), Estimating Equilibrium Exchange Rates, Washington, D.C., Institute for International Economics, p.19-60.
- Belloc, M. et D. Federici (2010), « A Two-Country NATREX Model for the Euro/Dollar », Journal of International Money and Finance, 29(2) : 315-335.
- Bergsten, F., O. Davanne et P. Jacquet (1999), « The Case for Joint Management of Exchange Rate Flexibility », Working Paper no 99-9, Institute for International Economics.
- Black, S. (1994), « On the Concept and Usefulness of the Equilibrium Rate of Exchange », in Williamson, J. (éd.)., Estimating Equilibrium Exchange Rate, Institute for International Economics, Washington, p. 279-292.
- Burda, M. et C. Wyplosz (1998), Macroeconomics : A European Text, Oxford University Press.
- Cartapanis, A. (2004), « Le déclenchement des crises de change : qu’avons nous appris depuis dix ans? », Economie internationale, 1 : 5-48.
- Cassel, G. (1925), « Rates of Exchange and Purchasing-Power Parity », Scandinaviska Kreditaktiebolaget Quarterly Report, avril : 17-21.
- Clark, P. B. et R. MacDonald (1999), « Exchange Rates and Economic Fundamentals : Methodological Comparison of BEERs and FEERs », in MacDonald, R. et J. Stein (éds), Equilibrium Exchange Rate, Kluwer Acamedic Publishers, p. 285-322.
- Clark, P. B. et R. MacDonald (2000), « Filtering the BEER : A Permanent and Transitory Decomposition », IMF Working Paper, no 144.
- Crouhy-Veyrac, L. et M. Saint-Marc (1995), « The Natural Real Exchange Rate Between the Franc and the Deutsche Mark : Implications for Monetary Union » in Stein, J. et P. Allen (éds), Fundamental Determinants of Exchange Rates, Oxford, Oxford University Press, p. 126-153.
- Darné, O. et J. F. Hoarau ( 2008), « Tester la validité de la parité des pouvoirs d’achat pour l’économie chinoise : une nouvelle analyse par les tests de racine unitaire », Recherches Economiques de Louvain, 72(2) : 219-236.
- De Gregorio, J. et H. G. Wolf (1994), « Terms of Trade, Productivity and the Real Exchange Rate », NBER Working Paper, no 4807.
- Detken, C., A. Dieppe, J. Henry, C. Marin et F. Smets (2002), « Determinants of The Effective Real Exchange Rate of The Synthetic Euro : Alternative Methodological Approaches », Australian Economic Papers, 41(4) : 404-436.
- Duval, R. (2001), « Les déterminants de long terme du taux de change réel », Thèse de doctorat, Paris I.
- Edwards, S. (1993), « Openness, Trade Liberalization, and Growth in Developing Countries », Journal of Economic Literature, 31(septembre) : 1358-1393.
- Edwards, S. (1994), « Real and Monetary Determinants of Real Exchange Rate Behavior : Theory and Evidence from Developing Countries », in Williamson, J. (éd.), Estimating Equilibrium Exchange Rates, Washington, D.C., Institute for International Economics, p. 61-92.
- Elbadawi, I. (1994), « Estimating Long-Run Equilibrium Real Exchange Rates », in Williamson, J. (éd.), Estimating Equilibrium Exchange Rates, Washington, D.C., Institute for International Economics, p. 93-132.
- Faruqee, H. P. Isard et P. R. Masson (1999), « A Macroeconomic Balance Framework for Estimating Equilibrium Exchange Rates », in MacDonald, R. et J. Stein (éds), Equilibrium Exchange Rate, Kluwer Acamedic Publishers, p.103-134.
- Fleming, W. H. et T. Zariphopoulou (1991), « An Optimal Investment/Consumption Model with Borrowing », Mathematics of Operations Research, 16(4) : 802-822.
- Gandolfo, G. et A. Felettigh (1998), « The NATREX : An Alternative Approach. Theory and Empirical Verifications », CIDEI working paper, no 52, Universita di Roma, La Sapienza.
- Hinkle, L. E. et P. Montiel (1999), Exchange Rate Misalignment : Concepts and Measurement for Developing Countries, Oxford University Press, New York.
- Hoarau, J.F. (2004), « Le mésalignement du taux de change réel dans le cadre d’une petite économie ouverte : causes, procédures d’estimation et politiques de correction. Une application à l’économie australienne », Thèse de doctorat, Université de La Réunion.
- Hoarau, J.-F. (2006), « Les régimes monétaires en Australie, 1977-2000 : une mise en perspective à l’aide d’un indicateur de distorsion du taux de change réel », Economie internationale, 105(premier trimestre) : 85-112.
- Hoarau, J.-F., N. Latchimy et A. Nurbel (2003), « Foreign Demand, Domestic Investment and Trade Balance : The Case of Australia », Journal of Business and Economic Research, 1(4) : 49-59.
- Isard, P. (1997), Exchange Rate Economics, Cambridge Surveys of Economic Literature.
- Isard, P. et H. Faruqee (1998), « Exchange Rate Assessment : Extensions of the Macroeconomic Balance Approach », Occasional Paper 167, IMF, Washington D. C.
- Joly, H. C. Prigent et N. Sobczak (1996), « Le taux de change réel d’équilibre : une introduction », Economie et Prévision, 123-124 : 1-21.
- Lim, G. et J. Stein (1995), « The Dynamics of the Real Exchange Rate and Foreign Debt in a Small Open Economy : Australia », in Stein, J., P. Allenetalii (éds), Fundamental Determinants of Exchange Rates, Oxford, Oxford University Press, p. 85-125.
- MacDonald, R. (1999), « What do we Really Know About Real Exchange Rates », in MacDonald, R. et J. Stein (éds), Equilibrium Exchange Rate, Kluwer Acamedic Publishers, Kluwer Academic Publisher, p. 19-66.
- MacDonald, R. et J. L. Stein (1999), Equilibrium Exchange Rates, Kluwer Academic Publishers.
- Malinvaud, E. (1987), « Capital productif, incertitudes et profitabilité », Annales d’économie et de statistiques, 5(janvier-mars) : 1-36.
- Marin Martinez, C. (2003), « The Structural Approach of Natrex Model on Equilibrium Exchange Rates », Documentos de Economia finanzas Internacionales, 03/03(octobre).
- Montiel, P. (1999), « The Long-Run Equilibrium Real Exchange Rate : Conceptual issues and Empirical Research », in Hinkle, L. E. et P. Montiel, Exchange Rate Misalignment : Concepts and Measurement for Developing Countries, Oxford University Press, New York.
- Rey, S. (2009), « L’apport du NATREX à la modélisation des taux de change d’équilibre : Théorie et application au dollar canadien », L’Actualité économique, Revue d’analyse économique, 85(2) : 131-181.
- Samuelson, P. (1964), « Theoretical Problems on Trade Problems », Review of Economics and Statistics, 46 : 145-154.
- Song, C. Y. (1997), « The Real Exchange Rate and the Current Account Balance in Japan », Journal of the Japanese and International Economies, 11(2) : 143-184.
- Stein, J. (1995), « The Natural Exchange Rate of the US Dollar and Determinants of Capital Flows », in Stein, J., P. R. Allenet alii (éds), Fundamental Determinants of Exchange Rate, Oxford, Clarendon Press, p. 38-84.
- Stein, J. (1999), « The Evolution of the Real Value of the US Dollar Relative to the G7 Currencies », in MacDonald, R. et J. Stein (éds), Equilibrium Exchange Rate, Kluwer Acamedic Publishers, Kluwer Academic Publisher, p. 67-102.
- Stein, J. (2006), Stochastic Optimal Control, Intemational Finance, and Debt Crisis, Oxford University Press, New York.
- Stein, J., P.R. Allenetalii (1995), Fundamental Determinants of Exchange Rates, Oxford, Clarendon Press.
- Stein, J. et G. Paladino (2001), « Exchange Rate Misalignments and Crises », Review of Economics, 52(2) : 111-151.
- Stein, J. et K. Sauernheimer (1995), « The Real Exchange Rate of Germany », Brown University Department of Economics Working Paper, no 96-13, Brown University.
- Stemitsiotis, L. (1992), Taux de change de référence et système monétaire international, Economica, Paris.
- Tobin, J. (1969), « A General Equilibrium Approach to Monetary Theory », Journal of Money Credit and Banking, 1 : 15-29.
- Williamson, J. (1985), The Exchange Rate System, MIT Press.
- Williamson, J. (1994), Estimating Equilibrium Exchange Rate, Washington, D.C., Institute for International Economics.
- You, F.K. et N. Sarantis (2008a), « An Extended NATREX Model for China », Discussion Paper, no 2008-2, Centre for International Capital Markets, London Metropolitan Business School, London Metropolitan University.
- You, F.K. et N. Sarantis (2012), « Structural Breaks and The Equilibrium Real Effective Exchange Rate of China : A NATREX Approach », China Economic Review, 23(4) : 1146-1163.
List of figures
Graphique 1
L’effet de l’imparfaite mobilité des capitaux avec λ4 petit
Graphique 2
L’effet de l’imparfaite mobilité des capitaux avec λ4 grand
Graphique 3
La dynamique du capital productif
Graphique 4
La dynamique de la dette extérieure
Graphique 5
Représentation graphique de l’équilibre dynamique



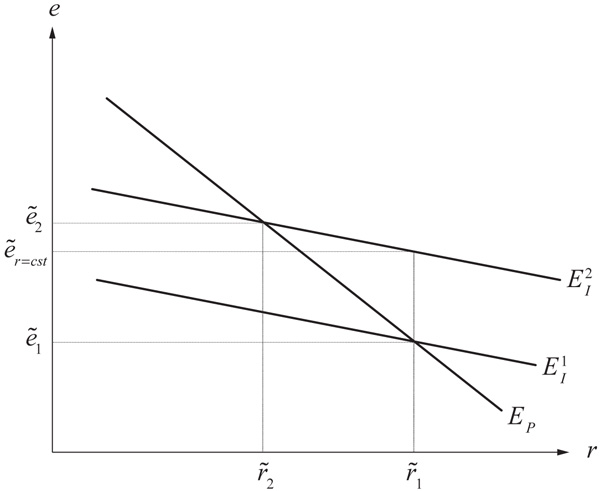


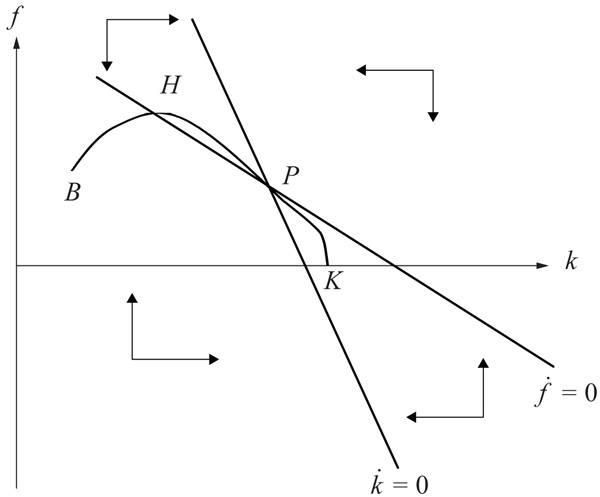
 10.7202/044252ar
10.7202/044252ar