Abstracts
Résumé
Il existe plusieurs critères d’information dont le but est de faciliter la sélection du modèle statistique représentant le mieux possible la réalité. Ces critères s’appliquent notamment au cas des modèles de séries chronologiques à une seule variable. La théorie asymptotique peut être utilisée pour faire un choix entre ces critères. Par exemple, si le modèle possède un ordre authentique, il peut être démontré que certains critères sont fortement convergents pour cet ordre. Historiquement, l’estimation en échantillon fini se base sur la sélection d’un ordre unique, même si plusieurs auteurs reconnaissent l’importance du cas où il n’existe pas de vrai ordre fini. Nous proposons ici un survol de la littérature sur les critères d’information et sur leur comparaison asymptotique et en échantillons finis. Nous présentons également quelques comparaisons de critères en échantillons finis en ne prenant pas pour acquis un ordre authentique au modèle. Nous utilisons alors une mesure de distance dans le but d’évaluer les performances de divers critères dans la sélection de modèles simulés. Cette mesure nous permet de juger l’exactitude de la sélection de l’ordre des modèles résultant de l’utilisation des critères (la sélection non optimale) par rapport à la sélection de l’ordre des modèles simulés (la sélection optimale). Ceci n’est pas possible dans le cas où l’on assume une forme vraie par rapport à laquelle on compare notre modèle.
Article body
Introduction
Ce texte a été écrit en mémoire de Marcel Dagenais. Il a produit un corpus important touchant les questions de spécification de modèle, erreurs de spécification et erreurs dans les variables. Quoique notre texte ne découle pas directement de ses travaux, les idées et les approches méthodologiques de Marcel Dagenais nous ont influencés de façon significative.
Les critères d’information de Akaike (1974), Hannan et Quinn (1979), Hurvich et Tsai (1989) et Schwarz (1978) sont basés sur l’échantillon observé et peuvent servir à sélectionner le meilleur modèle parmi un ensemble de modèles possibles. Lorsque le vrai processus générateur de données se trouve dans cet ensemble et que l’échantillon est assez grand par rapport au nombre de paramètres, le rôle de ces méthodes est clairement de l’identifier parmi toutes les possibilités contenues dans l’ensemble. Il est donc naturel de chercher à évaluer la convergence des différents critères, c’est-à-dire la convergence de l’ordre des modèles estimés par rapport à l’ensemble des vrais processus. L’étude de la convergence des critères d’information n’est pas un sujet nouveau. Il est bien connu que le critère d’information d’Akaike (AIC) n’est pas convergent pour l’ordre réel des modèles de séries chronologiques mais il peut être démontré que d’autres méthodes, telles que les critères de Schwarz et Hannan et Quinn, sont convergentes dans ces circonstances.
Il est possible que des méthodes alternatives résultent en des conclusions radicalement différentes dans des échantillons finis, même lorsqu’elles sont toutes convergentes. Ainsi, nous désirons évaluer les propriétés des divers critères en échantillons finis de manière à identifier ceux offrant les meilleures performances pour certaines classes de problèmes. Comme c’est le cas en théorie asymptotique, il est de mise, lors de l’évaluation de la performance des critères de sélection en échantillon fini, de se demander quel critère sélectionne le vrai processus générateur de données (PGD) le plus souvent. Il s’agit de l’approche habituellement utilisée pour les problèmes en échantillons finis. Cependant, il est également possible que le PGD soit tel qu’il n’existe aucun ordre précis qui puisse le représenter, comme c’est le cas, par exemple, des approximations d’ordre fini de processus autorégressifs d’ordre infini. Ces cas de modèles d’ordre infini expliquent l’intérêt porté par la littérature au critère d’Akaike malgré son manque de convergence quand le modèle est d’ordre fini et existe[1]. Les comparaisons s’appuyant sur des simulations de processus d’ordre fini peuvent alors mener à un choix de critère non optimal. Malgré cela, un ordre fini est généralement postulé dans la plupart des comparaisons effectuées dans des échantillons contenant un petit nombre d’observations.
Cependant, il importe tout autant de pouvoir évaluer les performances des critères d’information lorsque l’ordre théorique ou la forme du modèle n’existent pas dans la classe de modèles considérée. Peu de résultats sont connus dans ces cas. Il est alors nécessaire d’utiliser une méthode différente des méthodes de simulation discutées ci-haut pour arriver à comparer la performance relative de différents critères de sélection. L’utilisation du critère d’information de Kullback-Liebler moyen (KLIC) est considéré par Sin et White (1996). Leurs conclusions incluent plusieurs résultats sur la convergence de fonctions de pénalité. Au cours d’une revue des applications des mesures de distances à des problèmes économétriques, Galbraith et Zinde-Walsh (2001) proposent d’utiliser de telles mesures entre les modèles estimés et le vrai PGD comme indicateur de la performance des critères d’information. Cet article suggérait l’utilisation d’une mesure de distance et en démontrait le potentiel pour l’évaluation des critères d’information. Il incluait aussi une brève étude par simulation. Le présent article poursuit la même idée en évaluant la performance de quelques critères d’information dans le cadre de la sélection de l’ordre adéquat de modèles autorégressifs. Les processus générateurs de données considérés ont des formes ARMA, avec des composantes de moyenne mobile non nulles, de sorte qu’il n’existe pas d’ordre correct pour les approximations par les modèles autorégressifs. L’utilisation d’une mesure de distance nous permet de juger la proximité des modèles non optimaux par rapport au modèle optimal, chose impossible lorsque les modèles ne sont caractérisés qu’en tant que « vrai » ou « faux ».
La première partie de cet article offre une revue des quelques critères d’information parmi les plus importants, certains convergents et d’autres non convergents, au sens défini plus haut. Pour chacun d’entre eux, les conditions de convergence sont décrites lorsqu’elles existent. La deuxième partie résume l’état des connaissances sur les performances relatives des critères d’information dans des échantillons finis. Ces résultats se basent en grande partie, mais pas totalement, sur l’hypothèse de l’existence d’un ordre réel pour le PGD. Ainsi, ces deux sections offrent un résumé des connaissances actuelles sur les performances asymptotiques et en échantillons finis des instruments de sélection de modèles statistiques. La troisième partie examine le cas d’un modèle pour lequel aucun ordre authentique n’existe en considérant l’approximation de modèles autorégressifs d’ordre infini par des modèles autorégressifs d’ordre fini. Cette section débute par une courte introduction aux notions de mesures de distance qui y sont utilisées. Nous concluons que, dans de telles situations, les meilleurs guides dans la sélection de l’ordre d’un modèle en échantillon fini sont les critères menant aux formes plus simples tels que les critères de Bayes et de Schwarz, bien que le critère d’Akaike soit généralement considéré comme étant le plus adéquat.
1. Les critères d’information et leurs propriétés asymptotiques
Le choix d’un modèle parmi une classe de modèles alternatifs (pouvant contenir le vrai modèle ou non) ne peut être effectué à partir d’une comparaison entre les valeurs estimées de la fonction d’objectif (comme, par exemple, la fonction du maximum de vraisemblance) puisque ces fonctions impliquent une forme particulière pour le modèle. Typiquement, les critères de sélection ajoutent une fonction de pénalité à la fonction d’objectif. Les principes les plus importants sur lesquels sont construits les critères de sélection de modèles sont basés sur des mesures d’information telles que des mesures de risque, de longueur de codage, des critères bayésiens et des prédictions d’erreur[2]. La validité des critères peut être évaluée par rapport à certaines considérations asymptotiques. Ces considérations sont : premièrement, si le bon modèle a une probabilité limite d’être choisi égale à un s’il est un élément de l’ensemble de modèles considérés; deuxièmement, si le « meilleur » modèle parmi tous les modèles incorrects est choisi de façon convergente lorsque le bon modèle ne fait pas partie des alternatives considérées. Il est à noter que le second point peut autant être appliqué au cas où le vrai modèle est inclus qu’à celui où il ne l’est pas alors que le premier point est limité au cas où le vrai modèle est inclus. Un troisième point à considérer est l’efficacité asymptotique dans la sélection d’une approximation d’ordre fini d’un processus d’ordre infini. Ce point ne repose aucunement sur l’existence d’un ordre vrai.
1.1 Quelques critères importants
Le principe général d’information utilisé pour la construction de critères d’information est basé sur la divergence entre deux fonctions de densité, f et g,
On peut interpréter cette quantité comme étant une mesure du risque impliqué par la possibilité de choisir une fausse densité g au lieu de la bonne densité f. Alternativement, elle peut également représenter la surprise de découvrir que g est la vraie densité lorsque f avait été considérée comme la vraie. Si les deux densités font partie d’une classe paramétrique et que g contient k paramètres, il est possible d’obtenir une approximation de I(f;g) en utilisant la méthode du maximum de vraisemblance dans un échantillon de taille T :
Il s’agit de l’équation utilisée par Akaike (1974) pour obtenir le critère d’information d’Akaike (AIC). Ce critère est appliqué dans le contexte des séries chronologiques sous la forme suivante
où k représente l’ordre d’un processus AR ou la somme des ordres AR et MA dans un modèle ARMA[3]. De nombreuses modifications au AIC sont proposées dans la littérature. En particulier, notons le AIC corrigé (AICC) (Suguira, 1978; Hurvich et Tsai, 1989). Le AICC de Hurvich et Tsai peut être écrit comme suit
La correction se rapporte au biais d’estimation de l’information de Kullback-Leibler effectuée dans le AIC. Il est a noter que ce critère corrigé est fréquemment écrit sous la forme d’une somme du AIC et d’une pénalité non stochastique supplémentaire mais que Hurvich et Tsai écrivent le AIC sous une forme qui est une transformation de celle donnée ici, mesurée par T. Il est donc important d’être prudent dans l’application de la pénalité additionnelle.
Des critères d’information bayésiens peuvent être dérivés à partir de distributions a priori. Le critère d’information bayésien (BIC) le plus utilisé est
où la différence avec le AIC se situe dans la fonction de pénalité. Schwarz (1978) a dérivé ce critère (le BIC) à partir de distributions a priori de la famille Koopman-Darnois. Dans le contexte des processus ARMA, le BIC devient
Une fois de plus, plusieurs modifications existent. Rissanen (1987, 1988) explore une autre approche de l’information basée sur le principe de la description des données la plus courte (shortest data description) découlant de la théorie de l’encodage de Shannon. Le critère de Rissanen résultant de cette approche est similaire au BIC.
Hannan et Quinn (1979) proposent un critère (HQ) pour les processus ARMA qui peut être considéré comme un intermédiaire entre le AIC et le BIC. En effet, le HQ adoucit quelque peu la sévérité de la fonction de pénalité du BIC relativement à la croissance de la taille de l’échantillon tout en maintenant une forte convergence dans l’identification de l’ordre réel du modèle. Le coût de ces améliorations est l’obligation de choisir une valeur pour le paramètre c (supérieure à 1) :
Malheureusement, il existe très peu d’information susceptible d’aider au choix de la valeur de c. Plusieurs études, parmi lesquelles celle de Hannan et Quinn, utilisent la valeur limite de c = 1 pour conduire des expériences de simulation, en dépit du fait que la preuve de la convergence de HQ requière que c soit strictement supérieur à 1.
Un autre principe de sélection est celui de la minimisation du FPE, l’erreur de prédiction finale d’un modèle de séries chronologiques potentiellement incorrectement spécifié. La pénalité en résultant est similaire à celle du AIC quoique typiquement plus parcimonieuse :
Un critère similaire, celui de Mallows (1973), dénoté par Cp, est applicable au contexte des régressions.
L’ensemble des critères d’information discutés ici sont ceux qui seront examinés dans l’étude comparative qui suit.
1.2 Propriétés asymptotiques
De façon générale, une fois que la forme du modèle et la dimension des paramètres sont connus pour les modèles (par exemple, l’ordre d’un modèle ARMA stationnaire ou l’ensemble des régresseurs dans un modèle linéaire), plusieurs méthodes permettent d’obtenir des estimations convergentes et asymptotiquement normales. Ces faits suggèrent que l’emphase devrait être désormais placée sur la convergence d’un critère d’information, c’est-à-dire, sur la sélection du bon ordre pour le modèle à être estimé. De plus, ceci suggère que le vrai modèle est un élément de la classe de modèle à laquelle le critère est appliqué.
Hannan et Quinn (1979) présentent des conditions s’appliquant aux fonctions de pénalité et suffisantes pour la convergence de la sélection de l’ordre pour des modèles de type ARMA. Selon cette approche, il a été démontré que les critères AIC, AICC, FPE et Cp sont tous non convergents (voir Choi, 1992, pour les références). Les autres critères considérés, c’est-à-dire les BIC, SIC et HQ, sont fortement convergents.
Comme nous le mentionnions plus tôt, le fait qu’il soit possible que le vrai modèle ne soit pas contenu dans la classe de modèles considérés rend les arguments basés sur la seule convergence asymptotique insuffisants pour classer les critères les uns par rapport aux autres. Par exemple, le fait que le AIC choisit systématiquement des modèles d’ordre plus élevé que ceux choisis par les autres critères peut se transformer en avantage dans les cas où le vrai modèle possède une dimension paramétrique infinie, relativement à la classe de modèles considérés, au lieu d’une dimension finie. Cependant, comme nous le verrons plus tard, d’autres critères peuvent offrir de meilleures performances que le AIC dans l’exercice de sélection d’un ordre fini pour un modèle devant servir d’approximation à un modèle de séries chronologiques n’ayant pas d’ordre fini, à condition qu’une définition convenable de l’ordre fini optimal soit établie.
Une telle définition constitue une façon de comparer des modèles même lorsque le vrai modèle n’est pas inclus dans la classe de modèles considérée. Par exemple, dans leur article sur la convergence des critères d’information, Sin et White (1996) définissent la convergence comme étant la sélection du modèle minimisant le critère d’information de Kullback Leibler moyen (KLIC). Cette approche de la convergence n’est pas conditionnelle à l’inclusion du vrai modèle. Le modèle choisi est simplement celui de la classe étant le plus rapproché du vrai modèle dans le sens précis de la minimisation de l’espérance mathématique du KLIC. Sin et White suggèrent des conditions s’appliquant à la fonction de pénalité ĉT pour obtenir la faible ou la forte convergence dans les critères d’information par rapport au KLIC moyen dans une large classe de modèles. Pour obtenir la forte convergence dans le cas des processus ARMA, il est alors nécessaire d’avoir une fonction de pénalité possédant un taux de croissance, et une pénalité sur les paramètres en trop, qui sont similaires à ceux obtenus par Hannan et Quinn.
Bien que la convergence lorsqu’un vrai ordre existe soit une propriété désirable, la propriété de convergence générale s’obtient seulement pour les critères sacrifiant l’efficacité asymptotique dans la sélection d’approximation de processus de dimension infini en échantillons finis (par exemple, voir Hannan et Quinn, 1979 et Schwarz, 1978). Dans cette optique, l’efficience asymptotique tient pour, entre autres, les critères AIC, AICC et FPE (Hurvich et Tsai, 1989). Nous pouvons donc anticiper que ces critères offriront de bonnes performances lorsque testés dans le cadre de problèmes où les modèles ne possèdent pas d’ordre réel, comme ce sera le cas dans le reste de cet article. Toutefois, comme nous l’avons déjà mentionné, ce potentiel ne se démarque pas clairement dans nos résultats.
2. Évaluation de critères d’information pour la sélection de modèles en échantillon fini
L’évaluation des critères d’information en échantillons finis se fait généralement par l’observation de l’ordre sélectionnée selon les critères appliqués à des données générés par des simulations de processus connus. Typiquement, ces processus sont d’un ordre fini et relativement petit. Cependant, quelques auteurs, Hannan et Quinn (1979) par exemple, pour les modèles AR, ont étudié les performances des critères dans des cas où il n’existe pas de vrai ordre fini. Des études de simulation de ce type sont Hannan et Quinn (1979), Geweke et Meese (1981), Lütkepohl (1985), Koehler et Murphree (1988), Mills et Prasad (1992), Ducharme (1997) et Anderson et al. (1998). Comme le présent article, toutes ces études traitent du problème de l’estimation de la meilleure représentation d’un processus et non pas de l’estimation d’une caractérisation d’un processus de nuisance à utiliser dans des tests d’hypothèses. Au contraire, Ng et Perron (2001) traitent de l’ordre de processus autoregressifs dans le cadre des tests d’hypothèses. L’ordre optimal d’un modèle peut être sensiblement différent lorsque le but du chercheur est la mesure de la taille d’un test d’hypothèse.
Même si Hannan et Quinn (1979) ne s’occupent que du critère qu’ils proposent, leur approche à néanmoins l’intérêt d’être parmi les premières à s’intéresser au cas où l’ordre du vrai modèle n’est pas fini. En particulier, en plus d’un processus AR d’ordre 1, ils considèrent un processus MA(1) non inversible pour lequel il n’existe pas d’ordre fini. Dans ce cas, comme dans celui où l’ordre du modèle est 1, le critère de Hannan et Quinn indique des modèles d’ordre en moyenne moins élevés que le AIC.
Lütkepohl (1985) compare des critères dans le cadre de modèles autorégressifs vectoriels (VAR). Son article est particulièrement exhaustif et il compare les critères autant par la fréquence avec laquelle ils choisissent le bon ordre que par leur erreur moyenne de prévision. Le critère de Schwarz ainsi qu’une version du critère de Hannan et Quinn se détachent clairement des autres comme étant les plus performants selon ces tests. On trouve aussi des comparaisons entre plusieurs critères dans Hurvich et Tsai (1989), particulièrement par rapport au AIC corrigé qu’ils introduisent. Bien qu’ils considèrent le cas où le processus n’est pas de dimension finie, leur étude est basée sur la fréquence de sélection du bon ordre du modèle, où il est accepté qu’un modèle d’ordre fini existe dans la classe de modèles considérée. Ils concluent que le AICC choisit le bon modèle le plus souvent.
Mills et Prasad (1992) comparent plusieurs critères d’information, parmi lesquels le AIC, AICC, le critère de Schwarz, celui de Hannan et Quinn, le critère de longueur minimale de description (Rissanen, 1987, 1988) et plusieurs autres. Ces comparaisons se basent sur deux classes de processus : (i) des processus autorégressifs d’ordre 3, pour lesquels la classe de modèles considérés est celle des processus autorégressifs d’ordre allant jusqu’à 8; (ii) des processus générés par quatre variables causales, pour lesquels la classe de modèles considérés consiste en un sous-ensemble de ces quatre variables plus quelques variables n’ayant rien à faire avec le PGD. Dans ces deux cas, il existe un vrai modèle, d’ordre 3 et 4 respectivement. Mills et Prasad considèrent l’ordre sélectionné par différents critères ainsi que l’erreur de prédiction moyenne commise par les modèles choisis.
Plusieurs conclusions intéressantes ressortent. Premièrement, comme dans plusieurs études mentionnées plus haut, il est évident que le SIC a tendance à sélectionner des dimensions plus petites que le AIC et le AICC dans les contextes des modèles AR et des régressions. De plus, il semble que le AIC ait une forte tendance à choisir des ordres trop élevés. Deuxièmement, les différences dans la mesure de l’erreur de prédiction moyenne sont petites, particulièrement lorsque comparées à la différence moyenne entre les tailles sélectionnées des modèles. Ceci est en contradiction avec les résultats de Anderson et al. (1998) qui, en comparant le AIC et le AICC, trouvent une tendance considérable au AICC avec la correction de Hurvich-Tsai à sous-paramétriser les modèles. Ces auteurs présentent également quelques résultats prometteurs, quoique non définitifs, pour un critère basé sur la longueur minimale de description de Rissanen. De façon générale, cependant, aucune indication claire de la dominance d’un critère particulier n’existe.
King et Bose (2002) comparent la performance de critères de sélection de modèles dans un contexte de régression et obtiennent des résultats similaires à ceux mentionnées ci-haut pour les modèles de séries chronologiques. Ils évaluent plusieurs critères possédant des fonctions de pénalité similaires à celle du AIC tels que le Cp, de Mallows, le BIC, le SIC et le HQ ainsi qu’une nouvelle méthode sur la base de la probabilité du choix du bon processus. Bien qu’aucun critère ne domine les autres, le BIC présente, de façon générale, les meilleurs résultats, suivi du HQ. La probabilité que le Cp ou le AIC sélectionnent le bon modèle est sensiblement moins élevée.
Dans la prochaine section, nous présentons plus d’information sur la performance relative sous la forme de résultats traitant de manière explicite du cas où il n’existe pas d’ordre réel, de sorte que la performance des critères d’information doit être jugée d’une autre façon que par le nombre de fois où il choisit le bon modèle.
3. Sélection de modèles autorégressifs quand il n’existe aucun ordre fini
Lorsque la classe de modèles considérée ne contient pas le vrai modèle, il est nécessaire de trouver une unité de mesure de l’adéquation de l’estimation sélectionnée par rapport à la réalité. C’est ce que nous faisons dans la présente section, où nous considérons la sélection de modèles AR ayant une partie MA, ce qui fait en sorte que la vraie représentation du modèle ne fait pas partie de la classe considérée (les AR). Nous utilisons ici la mesure de Hilbert puisqu’il s’agit d’une mesure bien adaptée aux processus stochastiques stationnaires. La mesure de Hilbert ainsi que celle de Kullback-Leibler sont discutées dans Galbraith et Zinde-Walsh (2002) et, suivant cette présentation, nous débutons par une révision de la distance de Hilbert que nous utiliserons plus tard ainsi que ses applications à la classe des modèles ARMA que nous utiliserons par la suite. Nous nous concentrons sur la distance de Hilbert parce qu’elle s’applique naturellement à la représentation des innovations des processus ARMA. Pour une revue plus large et plus complète de la littérature sur les mesures de distances et sur la théorie de l’information, voir, par exemple, Ullah (1996).
3.1 Mesure de la qualité de l’approximation du vrai modèle
Soit un processus stochastique {Xt} en temps discret. L’espace des processus stochastiques ayant une moyenne zéro et une variance finie peut être représenté par un espace de Hilbert, H, muni du produit scalaire (X, Y) défini par E(XY) et la norme de Hilbert ∥X∥ définie par [E(X2)]½. Les valeurs du processus {Xt}, pour t à l’intérieur d’un ensemble d’index, existent dans un sous-ensemble Hx ⊂ H de l’espace de Hilbert. Ce sous-ensemble Hx est lui-même un espace de Hilbert.
Puisque l’espace des processus stochastiques stationnaires du second degré est un espace de Hilbert, la distance entre deux processus X et Y peut être mesurée par la norme de la différence dH(X, Y) = ∥X – Y∥ = [E(X – Y)2]½. Dans cette optique, une caractéristique importante de l’espace de Hilbert est qu’il nous laisse définir la distance d’un processus à une classe de processus (ou la distance entre les classes de processus). Pour calculer cette distance, il suffit de minimiser la distance avec tous les processus de la classe.
Quand nous travaillons avec des processus stationnaires, la distance entre les processus peut également être obtenue par les représentations des innovations des processus, c’est-à-dire, les représentations en fonction des processus stationnaires non corrélés (la base orthogonale {et}∞-∞). Si Xt = ∑∞i=0 βiet-i et Yt = ∑∞i=0 ξi εt-i avec εt = et, alors dH(X, Y) = ∥X – Y∥ = [∑∞i=0 (βi - ξi)2]½ σe, où ∥et∥ = σe, l’écart type de {et}. En plus d’imposer que les variances soient égales pour εt et et, nous posons aussi que σe = 1.
Nous considérons des processus ARMA stationnaires et inversibles. Soit l’opérateur de retard L tel que LZt = Zt-1, nous pouvons alors représenter ces processus sous la forme de fonctions d’innovations Zt = f(L) et, où et est un bruit blanc fort et f(L) est un polynôme rationnel tel que f(L) = Q(L) / P(L) où Q et P sont les polynômes de retard pour les parties MA et AR, c’est-à-dire, P(L) = I – α1L – ... – αpLp, et Q(L) = I + θ1L + ... + θqLq. Un processus ARMA(p, q) peut être écrit comme P(L) Zt = Q(L)et, et est stationnaire (inversible) si et seulement si les racines des polynômes P(L) (Q(L)) sont en dehors du cercle de rayon unité. Nous supposons que P(L) et Q(L) n’ont aucun facteur en commun.
Pour notre étude de processus ARMA d’ordre fini, il est important qu’un processus ARMA(p, q) de moyenne zéro et inversible représentant {Zt} puisse être estimé avec une relative exactitude par un processus AR(ℓ) pour un ordre ℓ, quelconque, puisqu’il est possible d’exprimer le processus comme étant une somme convergente des valeurs passées pondérées de Zt-i. Soit un polynôme MA inversible d’ordre k représenté par Qk(L). Ce polynôme possède une représentation AR d’ordre infini avec un polynôme autorégressif Pk(L) ʃ [Qk(L)]-1. Si Qk(L) = I + θ1L + ... + θkLk, alors Pk(L) = (I + θ1L + ... + θkLk)-1 = I – θ1L + (θ21 – θ2) L2 + ...= ∑∞i=0 γiLi. Soient νi l’inverse des racines de Qk(L). Notons que γi ≈ O(ν̄i), où ν̄ = max1≤i≤k∣νi∣, et ∣.∣ représente le modulus de la racine. Ainsi, pour un ordre ℓ du processus d’approximation assez grand, ∑∞ℓ+1 γ2i peut être rendu plus petit que n’importe quel δ choisit arbitrairement. Soit {Xt}, le processus AR(ℓ) dont les coefficients sont αi = γi, i = 1, ..., ℓ. Alors, ∥Z – X∥ = ∥Z – Y + Y – X∥ ≤ ∥Z – Y∥ + ∥Y – X∥ = (∑∞k+1 β21)½ + (∑∞ℓ+1 γ2i)½. Ainsi, il est possible de trouver un processus AR(ℓ) arbitrairement rapproché de {Zt} selon la distance de Hilbert.
Par exemple, soit un processus MA(q) inversible Zt = et + ∑qj=1 θjet-j, avec var(et) = 1. Ce processus peut être estimé par le processus AR(p) suivant : Xt = ∑pj=1 αj Xt-j + εt ayant var(εt) = σ2, et minimisant la distance de Hilbert. Lorsque p → ⋅, la distance de Hilbert entre {Zt} et {Xt} approche zéro, σ → 1, et les q premiers coefficients {αj} approchent les valeurs α1 = θ1, α2 = –θ1α1 + θ2, αi = –θ1αi-1 – θ2αi-2 – ... – θi-1α1 + θi pour i ≤ q, et αj = ∑qi=1 – θiαj-i pour j ≥ q + 1.
3.2 Évaluation des critères d’information en échantillons finis
Nous utilisons maintenant cette mesure de distance pour examiner les performances de quelques critères d’information dans le contexte de la sélection du meilleur modèle AR(ℓ) compte tenu que le vrai processus est un ARMA. Puisqu’il n’existe pas de vrai ordre dans les exemples que nous allons considérer, il est difficile de dire a priori quel résultat doit être considéré comme le plus favorable pour un critère d’information. En d’autres termes, il n’existe pas de « bonne réponse ». Cependant, il est possible d’utiliser la distance de Hilbert pour fabriquer une balise par rapport à laquelle les critères pourront être comparés. Ainsi, le résultat « optimal » sera défini comme l’identification de l’ordre optimal (au lieu de « vrai ») du modèle, qui sera défini comme celui menant à l’estimation de modèles étant le plus près possible, en moyenne, du vrai processus.
Il existe bien sûr d’autres façons d’établir des critères d’évaluation de modèles; nous pourrions, par exemple, ordonner en fonction de la distance moyenne entre modèles estimés et véritables à travers des simulations, plutôt que de tenter d’identifier, en premier lieu, un modèle « optimal ». Nous choisissons cette dernière approche toutefois, afin de souligner la différence entre modèle optimal et processus générateur de données, et afin de fournir des résultats comparables à ceux qui ont déjà été établis, et dans lesquels on mesure le degré de succès de l’identification du PGD véritable.
Ainsi, notre étude nécessite deux étapes : premièrement, il nous faut déterminer l’ordre optimal pour chacun des ensembles de processus ARMA(1,1) et pour les processus ARMA(2,1) et (1,2) possédant chacun une paire de racines complexes. Nous faisons cela de la manière suivante. Nous simulons un grand nombre de processus ARMA et pour chacun d’eux, nous estimons des processus AR(ℓ), ℓ = 1 ... L. Pour chacun des modèles estimés avec une taille d’échantillon donnée, nous calculons la distance entre ce modèle et le vrai processus. Nous obtenons ensuite la distance moyenne entre les modèles d’un ordre donné estimés et le vrai processus en calculant la moyenne des distances obtenues par un grand nombre de simulations (ici, 10 000). Le modèle optimal pour chaque taille d’échantillon et pour chaque combinaison de paramètres est celui dont l’ordre ℓ minimise la distance.
Cette première étape nous permet de définir le but que nous cherchons à atteindre par l’utilisation des critères d’information. C’est-à-dire que, même s’il n’existe pas de vrai ordre à choisir, nous pouvons déterminer un ordre optimal. Alors, les critères pourront être évalués par rapport à leur capacité à choisir l’ordre optimal. Dans la deuxième étape, noue calculons chaque critère d’information sur des échantillons simulés avec les modèles ARMA utilisant les paramètres et les tailles d’échantillon tels que définis à l’étape 1. L’ordre moyen sélectionné par chaque critère au cours des expériences de simulations est comparé avec l’ordre optimal obtenu à l’étape 1.
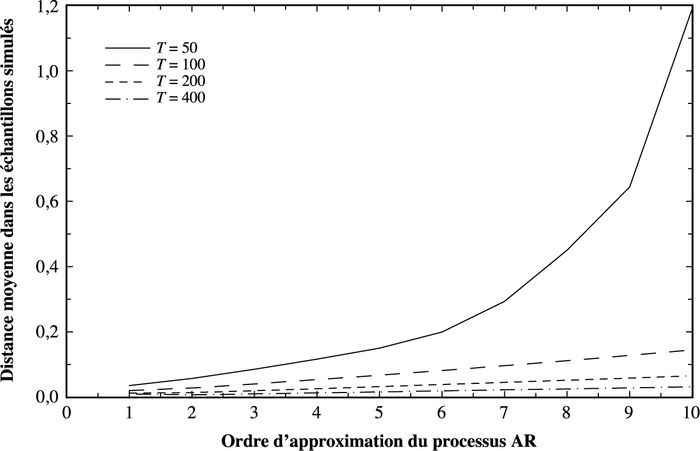
Le modèle optimal peut être lu à partir des graphiques, pour chacun desquels un processus ARMA différent est simulé. Les ordres AR considérés sont enregistrés sur l’axe inférieur avec un ordre maximum L = 10. Les graphiques (1 à 6) montrent chacun la distance moyenne entre les modèles AR estimés et le vrai processus, tel que décrit après 10 000 réplications. Quatre tailles d’échantillon sont considérées, T = {50, 100, 200, 400}. La distance moyenne pour chaque ℓ diminue à mesure que la taille de l’échantillon augmente, ce qui reflète la meilleure estimation possible avec des échantillons plus grands. Il est à noter que le minimum de ces graphes de distances moyenne change avec la taille de l’échantillon. Avec un échantillon plus large, un modèle d’ordre supérieur peut être optimal car il utilise plus d’information. Ceci constitue un aspect important du présent problème où il n’existe pas d’ordre vrai.
Graphique 1
Paramètre AR et MA 0,2 et 0,2 – distance approximative vs ordre AR
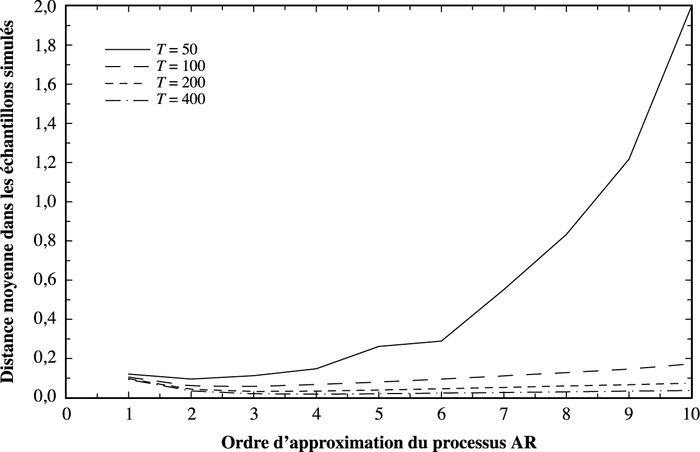
Graphique 2
Paramètre AR et MA 0,2 et 0,8 – distance approximative vs ordre AR
Graphique 3
Paramètre AR et MA 0,8 et 0,8 – distance approximative vs ordre AR
Graphique 4
Paramètre AR et MA 0,8 et -0,5 – distance approximative vs ordre AR
Graphique 5
Cas d’une racine AR complexe – distance approximative vs ordre AR
Graphique 6
Cas d’une racine MA complexe – distance approximative vs ordre AR
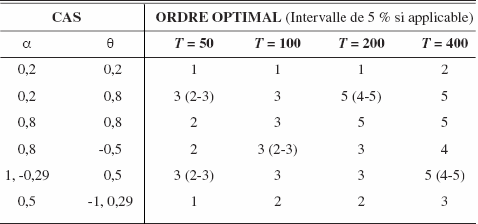
Le tableau 1 montre les paramètres des expériences de simulation et les valeurs de k minimisant les fonctions présentées dans les graphiques (dans les cas des ARMA(2,1) et (1,2), les racines du polynôme de deuxième degré sont 0,5 ± 0,2i). Dans de plus grands échantillons, les graphiques indiquent que les fonctions sont plutôt plates pour une grande région de k; cela est dû en partie au fait que l’échelle utilisée soit adéquate pour plusieurs distances moyennes. Toutefois, dans certains cas, la distance moyenne entre le vrai processus et le modèle estimé peut être très peu variable sur des intervalles de k. Ainsi, en plus des valeurs minimisant la distance, nous rapportons également les valeurs de k pour lesquelles la distance moyenne est contenue dans un intervalle de 5 pour cent de la valeur optimale (ces valeurs sont les intervalles présentés entre parenthèses) lorsqu’un espace de plus d’une valeur existe. Dans de tels cas, nous pouvons considérer un choix de modèle contenu dans cet intervalle comme optimal même si la vraie valeur minimisant la distance n’est pas atteinte.
Tableau 1
Ordre optimal du modèle AR par cas et taille d’échantillon – processus ARMA avec paramètres AR, MA α, θ
Les graphiques montrent clairement que les graphes des distances sont approximativement plates sur des sections de plus en plus larges à mesure que T augmente (nous rediscuterons de ce point plus tard); cependant, il est à noter qu’il existe relativement peu de cas dans lesquels les valeurs de k contenues dans le voisinage de l’optimum produisent des distances moyennes rapprochées à moins de 5 pour cent de l’optimum. Pour chaque cas, l’ordre optimal augmente de façon monotone en T.
Nous considérons maintenant les résultats moyen et médian d’un ensemble de critères d’information tels que décrit ci-haut : le AIC, AICC, Schwarz (SIC), bayésien (BIC), erreur de prédiction finale (FPE) et Hannan et Quinn (HQ)[4]. Le tableau 2 rapporte l’ordre moyen et médian sélectionné par les différents critères pour les simulations et les tailles d’échantillons présentées au tableau 1. Les critères sont présentés par ordre de parcimonie. Pour T = 50, dans le but d’éviter des modèles contenant trop de paramètres relativement au nombre d’observations, l’ordre maximum que nous permettons est ℓ = 10. La nécessité de telles restrictions sur la taille des modèles, surtout en échantillons finis, est discutée en détail par Hurvich et Tsai (1989).
Tableau 2
Ordre médian et moyen sélectionné par cas, taille d’échantillon et méthode – processus ARMA avec paramètres AR, MA α, θ
Note : L’astérisque « * » indique que la sélection médiane est optimale dans le sens où l’ordre est le même que celui défini au tableau 1 ou se trouve à l’intérieur de l’intervalle correspondant à une distance de 5 pour cent ou moins. Le « † » indique que l’ordre médian sélectionné diffère par plus ou moins 1 de l’ordre ou l’intervalle optimal tel que défini par le tableau 1.
Pour faciliter la comparaison entre le tableau 2 et les cibles présentées au tableau 1, nous adoptons la notation suivante. Si l’ordre médian rapporté au tableau 2 est l’ordre optimal, ou s’il correspond à l’intervalle présenté dans le tableau 1, alors, il est marqué par l’astérisque « * » et, par une croix « † », si l’ordre estimé tombe à plus ou moins un paramètre de l’ordre ou de l’intervalle optimal.
Nous utilisons les tableaux 1 et 2 ainsi que les graphiques pour tirer des conclusions. De toute évidence, la correspondance uniforme entre les résultats obtenus par les critères de BIC, SIC et les ordres optimum suggérés au tableau 1 est la meilleure. Le FPE et le HQ connaissent tous deux plusieurs bons résultats. Au contraire, le AIC et le AICC n’obtiennent pas de bons résultats. En effet, aucun des choix médians fait par l’un ou l’autre de ces critères ne correspond aux ordres optimum et ne se situe à plus ou moins un paramètre de l’optimum.
Toutefois, une attention plus profonde permet de tempérer ces conclusions. Les graphiques montrent clairement que le coût, en terme de distance, de l’incorporation de paramètres en trop est relativement petit (en considérant les échelles des graphiques et leurs effets sur les résultats en échantillons de grande taille, ce qui tend à éclipser les plus grandes distances moyennes pour T = 50). Cependant, le coût d’un ordre trop petit peut être important, surtout dans les petits échantillons. Ainsi, le coût d’utiliser les critères HQ ou FPE, qui sont typiquement moins parcimonieux, n’est pas nécessairement élevé, surtout dans de larges échantillons.
Cependant, dans chaque cas, le AIC sélectionne des ordres excédant considérablement l’ordre optimal. Grâce à son terme de correction, le AICC sélectionne des modèles moins distants de l’optimum, bien qu’ils soient aussi considérablement éloignés. Cette conclusion contredit Anderson et al. (1998), quoique le contexte ne soit pas le même. Aucune de ces mesures ne donne d’estimations sur cette classe de modèles, qui sont en compétition avec les méthodes plus précises. Contrairement à Mills et Prasad (1992), nous trouvons que la mesure du sacrifice impliqué est élevée dans plusieurs cas (comparez la distance moyenne des graphiques avec l’ordre des modèles typiquement estimés par les critères AIC et AICC).
Conclusion
Dans les cas où il n’existe pas d’ordre fini vrai dans la classe de modèles considérée, l’évaluation des performances de critères d’information ne peut se faire sur la base de la fréquence avec laquelle le bon modèle est sélectionné. De telles circonstances sont particulièrement importantes en séries chronologiques, où il existe des représentations autorégressives d’ordre non fini pour une grande classe de processus d’ordre fini plus généraux. Nous suggérons l’utilisation de la distance de Hilbert entre le vrai processus et le modèle estimé comme mesure du succès des critères de sélection. Même s’il n’existe pas de vrai modèle, nous pouvons déterminer un modèle optimal dont l’ordre est une fonction positive de la taille de l’échantillon, et dans le cas de modèles presque équivalents, nous pouvons définir un intervalle de modèles presque optimaux. Ces cibles sont ensuite utilisées pour comparer les performances de divers critères. Certains auteurs ont suggéré que les critères tels que le AIC pourraient offrir de bonnes performances dans les cas où il n’existe aucun vrai processus d’ordre fini. Nos résultats ne supportent pas cette théorie. Évidemment, le fait que le processus AR représentant le mieux le vrai processus soit d’ordre infini n’implique pas que le meilleur modèle en échantillon fini soit d’ordre infini. Nos résultats indiquent que le SIC et le BIC offrent les meilleures performances alors que le HQ et le FPE offrent également de bonnes performances (ceci est en accord avec d’autres auteurs, tels Lütkepohl). De tous les critères considérés ici, le AIC offre les moins bonnes performances considérant la classe de modèles étudiée.
Appendices
Remerciements
Nous remercions les Fonds québécois de la recherche sur la société et la culture (FQRSC), le Conseil de recherche en sciences humaines (CRSH) et le Centre Interuniversitaire de recherche en analyse des organisations (CIRANO) pour leur support financier de la présente recherche.
Notes
-
[1]
Par exemple, Buckland et al. (1997) suggèrent que « la philosophie sous-jacente aux critères AIC et AICC est que la “ vérité ” est d’un ordre dimensionnel élevé ne pouvant être décrite que par des modèles contenant plusieurs (possiblement une infinité) paramètres ».
-
[2]
Nous ne considérons içi que des critères basés sur l’information et non des alternatives tels que l’identification de modèles basés sur la fonction d’autocorrélation ou celle d’autocorrélation partielle (Box et Jenkins, 1976), ou sur des tests de la signification des composantes de modèles.
-
[3]
Il est a noter que nous utilisons (k) pour indiquer qu’une expression s’applique à un type de modèles particulier avec k termes, même si différents modèles avec k paramètres ont différentes valeurs. Par exemple, l’estimation de la variance ne sera pas la même pour un modèle ARMA(1,2) et pour un modèle ARMA(2,1), en dépit du fait que tous deux ont k = 3.
-
[4]
Le critère de Hannan-Quinn nécessite c > 1. Nous utilisons c = 1,1 bien que la valeur c = 1 soit souvent utilisée en pratique, entre autres, par Hannan-Quinn (1979). À mesure que c augmente, le critère tend à sélectionner des modèles de plus petit ordre. Avec c = 1, HQ sélectionne des modèles un peu plus petit que le AIC. L’obligation de choisir une valeur de c arbitraire est un défaut de cette méthode.
Bibliographie
- Akaike, H. (1974), « A New Look at the Statistical Model Identification », IEEE Transactions on Automatic Control, AC-19 : 716-723.
- Anderson, D.R., K.P. Burnham et G.C. White (1998), « Comparison of Akaike Information Criterion and Consistent Akaike Information Criterion for Model Selection and Statistical Inference from Capture-recapture Studies », Journal of Applied Statistics, 25 : 263-282.
- Box, G.E.P. et G.M. Jenkins (1976), Time Series Analysis: Forecasting and Control, 2e éd. Holden-Day, San Francisco.
- Buckland, S.T., K.P. Burnham et N.H. Augustin (1997), « Model Selection: An Integral Part of Inference », Biometrics, 53 : 603-618.
- Choi, B.S. (1992), ARMA Model Identification, Springer-Verlag, New York.
- Ducharme, G.R. (1997), « Consistent Selection of the Actual Model in Regression Analysis », Journal of Applied Statistics, 24 : 549-558.
- Galbraith, J.W. et V. Zinde-Walsh (2002), « Measurement of the Quality of Autoregressive Approximation, with Econometric Applications », in A. Ullah, A. Wan et A. Chaturvedi (éds), Handbook of Applied Econometrics and Statistical Inference, Marcel Dekker, New York, p. 401-421.
- Geweke, J. et R. Meese (1981), « Estimating Regression Models of Finite but Unknown Order », International Economic Review, 22 : 55-70.
- Hannan, E.J. et B.G. Quinn (1979), « The Determination of the Order of an Autoregression », Journal of the Royal Statistical Society Ser. B, 41 : 190-195.
- Hurvich, C.M. et C. Tsai (1989), « Regression and Time Series Model Selection in Small Samples », Biometrika, 76 : 297-307.
- King, M. et G. Bose (2002), « Finding Optimal Penalties for Model Selection in the Linear Regression Model », in Giles, D.E.A., (éd.), Computer-Aided Econometrics, Marcel Dekker, New York.
- Koehler, A.B. et E.S. Murphree (1988), « A Comparison of the Akaike and Schwarz Criteria for Selecting Model Order », Applied Statistics, 37.
- Kullback, L. et R.A. Leibler (1951), « On Information and Sufficiency », Annals of Mathematical Statistics, 22 : 79-86.
- Lütkepohl, H. (1985), « Comparison of Criteria for Estimating the Order of a Vector Autoregressive Process », Journal of Time Series Analysis, 6 : 35-52.
- Mallows, C.L. (1973), « Some Comments on Cp », Technometrics, 15 : 661-675.
- Mills, J.A. et K. Prasad (1992), « A Comparison of Model Selection Criteria », Econometric Reviews, 11 : 201-233.
- Ng, S. et P. Perron (2001), « Lag Length Selection and the Construction of Unit Root Tests with Good Size and Power », Econometrica, 69 : 1 519-1 554.
- Parzen, E. (1983), « Autoregressive Spectral Estimation », in D.R. Brillinger et P.R. Krishnaiah (éds), Handbook of Statistics, 3 : 221-247, North-Holland, Amsterdam.
- Rissanen, J. (1987), « Stochastic Complexity and Modelling », Annals of Statistics, 14 : 1 080-1 100.
- Rissanen, J. (1988), « Stochastic Complexity and the MDL Principle », Econometric Reviews, 6 : 85-102.
- Schwarz, G. (1978), « Estimating the Dimension of a Model », Annals of Statistics, 6 : 461-464.
- Shibata, R. (1980), « Asymptotically Efficient Selection of the Order of the Model for Estimating Parameters of a Linear Process », Annals of Statistics, 8 : 147-164.
- Sin, C.Y. et H. White (1996), « Information Criteria for Selecting Possibly Misspecified Parametric Models », Journal of Econometrics, 71 : 207-225.
- Suguira, N. (1978), « Further Analysis of the Data by Akaike’s Information Criterion and the Finite Corrections », Communications in Statistics, A7 : 13-26.
- Ullah, A. (1996), « Entropy, Divergence and Distance Measures with Econometric Applications », Journal of Statistical Planning and Inference, 49 : 137-162.
- Zinde-Walsh, V. (1990), « The Consequences of Misspecification in Time Series Processes », Economics Letters, 32 : 237-241.
List of figures
Graphique 1
Paramètre AR et MA 0,2 et 0,2 – distance approximative vs ordre AR
Graphique 2
Paramètre AR et MA 0,2 et 0,8 – distance approximative vs ordre AR
Graphique 3
Paramètre AR et MA 0,8 et 0,8 – distance approximative vs ordre AR
Graphique 4
Paramètre AR et MA 0,8 et -0,5 – distance approximative vs ordre AR
Graphique 5
Cas d’une racine AR complexe – distance approximative vs ordre AR
Graphique 6
Cas d’une racine MA complexe – distance approximative vs ordre AR
List of tables
Tableau 1
Ordre optimal du modèle AR par cas et taille d’échantillon – processus ARMA avec paramètres AR, MA α, θ
Tableau 2
Ordre médian et moyen sélectionné par cas, taille d’échantillon et méthode – processus ARMA avec paramètres AR, MA α, θ
Note : L’astérisque « * » indique que la sélection médiane est optimale dans le sens où l’ordre est le même que celui défini au tableau 1 ou se trouve à l’intérieur de l’intervalle correspondant à une distance de 5 pour cent ou moins. Le « † » indique que l’ordre médian sélectionné diffère par plus ou moins 1 de l’ordre ou l’intervalle optimal tel que défini par le tableau 1.