Le taux d’actualisation contre le principe de précaution? Leçons à partir du cas des politiques climatiques

Résumé

L’utilisation du calcul économique sur le très long terme fait l’objet de critiques qui peuvent aller jusqu’à un rejet pur et simple, en particulier en raison de la technique de l’actualisation qui, en écrasant le poids du long terme, viendrait en contradiction avec le principe de précaution. Nous expliquons ici, sur la base de l’expérience des débats autour du changement climatique, en quoi, appliquée en toute rigueur, l’actualisation est au contraire un point de passage obligé pour clarifier les enjeux de la décision. Nous montrons en particulier que, dans un cadre de décision séquentielle avec acquisition d’information, le choix, qui restera toujours controversé, du coefficient de préférence pure pour le présent, importe moins que les hypothèses sur la croissance, sur la productivité du capital, sur les préférences des agents et sur leurs « croyances » vis-à-vis des dommages climatiques. Nous concluons sur le fait que le taux de préférence pure pour le présent ne saurait résumer à lui seul les questions de solidarité avec les générations futures. Il convient aussi d’examiner la nature de ce que nous léguons aux générations futures, en particulier les stocks de capital physique et de connaissance qui déterminent leurs capacités d’adaptation à de futures informations.

Abstract

The application of standard cost-benefit analysis to evaluate long-term policies has been heavily criticized, in particular because of discounting, which is accused of putting too little weight on the future, thus contradicting the precautionary principle. Based on the example of climate mitigation policies, we show why discounting, rigorously applied, is necessary to clarify the issues at stake in the decision. In particular, we demonstrate that, within a sequential decision-making framework with increasing information, the value of pure time discounting matters less than the assumptions we make about future growth, productivity of capital, preferences and beliefs about climate change impacts. We conclude that intergenerational equity issues go beyond the value of pure time preference. We must also pay attention to the nature of our bequest to future generations, in terms of stocks of physical capital and of knowledge in particular, because it shapes their ability to adapt to new information.

Introduction

Le problème de l’effet de serre pose un défi singulier au calcul économique. Caractérisé par de très fortes incertitudes à la fois sur l’ampleur des dommages et sur les coûts des politiques de réduction des émissions de gaz à effet de serre, il porte sur un horizon temporel qui englobe plusieurs générations. Or, du fait de la double inertie des systèmes économiques et de l’accumulation des gaz à effet de serre dans l’atmosphère, attendre que la recherche scientifique réduise les incertitudes, c’est prendre le risque de décisions trop tardives, et il faut bien se résigner à décider « en méconnaissance de cause ». Voilà l’économiste requis d’informer la décision publique; mais, ce faisant, il prend le risque d’être accusé d’extrapoler sur le long terme, en s’abritant sur une technicité illusoire, les schémas du financier et de l’ingénieur optimisant un portefeuille ou une séquence d’investissements, et d’ignorer des principes éthiques comme la solidarité intergénérationnelle ou le « principe de précaution »[1].

L’objet de ce texte est d’examiner sous quelles conditions le calcul économique peut, malgré des difficultés évidentes, éclairer le débat public face à un défi si inédit. Sur de tels horizons, et en présence de tant d’incertitudes, l’enjeu est de coordonner les anticipations sur les différents futurs possibles en présence de fortes controverses scientifiques, éthiques, politiques. Loin de prétendre dicter « la bonne solution » dans un tel contexte, il peut en revanche constituer un « langage de négociation » (Henry, 1984) empêchant que ne l’emportent, sans plus ample examen et aux dépens de l’intérêt collectif, les acteurs disposant de la rhétorique la plus séduisante.

La controverse sur le statut du calcul économique dans l’examen des problèmes d’environnement à long terme est centrée sur la valeur du taux d’actualisation. Nous reviendrons donc tout d’abord sur les fondements de cette pratique, ce qui nous permettra d’expliquer, dans une seconde partie, pourquoi il serait dangereux de la disqualifier, même quand il s’agit de très long terme. Puis, dans une troisième partie, nous aborderons les problèmes spécifiques liés à l’incertitude, et montrerons que l’essentiel se joue sur l’adoption d’une problématique de décision séquentielle et sur la façon d’utiliser dans ce cadre les outils de l’analyse économique, ce que nous illustrerons à partir d’enseignements pour l’action à court terme tirés de trois exercices autour du couple incertitude – inertie.

1. Le taux d’actualisation, une variable dérivée de « visions du long terme »

La pratique standard du calcul économique consiste à établir la chronique, par rapport à un scénario de référence donné, des coûts et des bénéfices des différentes options politiques, puis à ne retenir que les options dont la valeur nette actualisée est positive :

(1)

Ceci confère un caractère central à la valeur du taux d’actualisation ρ. Vu le décalage temporel entre les coûts des politiques de réduction des émissions et leurs bénéfices (les dommages évités), on conçoit qu’émerge l’idée d’une contradiction fondamentale entre calcul économique et protection du climat : si ρ égale 8 %, chaque dollar non affecté à la protection du climat nous permettra de léguer 10 $ à nos enfants dans 30 ans et 47 $ à nos petits enfants dans 50 ans. À ce compte-là, il faudrait des dommages climatiques énormes pour justifier l’action; nos descendants seront en effet assez riches pour « se payer » les compensations nécessaires (par exemple déménager dans des zones moins touchées ou construire des digues).

Mais ceci revient à oublier que le taux d’actualisation reflète la tension entre la quantité d’épargne disponible pour financer l’investissement et la productivité présente et future de l’économie (Boiteux, 1969). Il ne prend donc sens qu’au sein d’une prospective où on s’assure de la cohérence entre la propension à épargner des agents, l’état présent et futur des techniques de production et le rythme de croissance qui en résulte. En fait, la formule simple dont nous sommes partis repose sur deux piliers qu’il faut bien garder à l’esprit.

Le premier est une métaphore, celle du planificateur bienveillant[2] auquel la société délègue la sélection du plan de consommation qui maximise le bien-être collectif. Ainsi mandaté, ce planificateur doit sommer à la fois les utilités individuelles des citoyens d’une même génération et celles des générations situées à des périodes différentes. Cela peut choquer le non-économiste, mais il faut se résigner au fait que toute décision revient bien à répartir des gains et des pertes entre individus différents dans le temps et l’espace, et que le choix n’est pas entre calculer ou pas, mais entre rendre ou non explicites, donc discutables, les bases du choix effectué. La fonction objectif du planificateur peut donc s’écrire comme suit, avec c_t,i le niveau de consommation de l’individu i de la génération t, U_t,i la fonction d’utilité de cet individu particulier et δ le taux d’actualisation de l’utilité (ou taux d’escompte social) :

(2)

avec

Dans cette équation, les poids α_i pondèrent les utilités des individus à l’intérieur d’une même génération et les facteurs d’actualisation q_i les utilités de générations différentes. Le choix des α_i est de nature politique puisqu’il traduit un jugement sur l’équité de la distribution actuelle des revenus. Avec des poids égaux à un, le planificateur maximisera le bien-être global en redistribuant massivement les revenus jusqu’à obtenir (avec des individus ayant des préférences identiques pour la consommation) égalité des revenus par tête. De même qu’une éthique égalitariste milite pour des α_i unitaires, il est alors tentant de conclure qu’un environnementaliste devrait militer pour des facteurs d’actualisation q_t égaux à 1, donc pour un taux d’escompte social δ nul, pour justifier l’action immédiate.

Mais une telle « liberté » est limitée par le deuxième pilier logique qui sous-tend l’équation (1), à savoir un modèle de croissance qui traduit les contraintes technico-économiques avec lesquelles le planificateur doit travailler. Ces contraintes peuvent être résumées dans le modèle suivant où, à chaque période de temps la combinaison des facteurs travail L et capital K permet la production d’un bien composite Y (3). La production du bien composite est répartie entre consommation C et investissement I (4), et l’investissement permet d’accroître le stock de capital à la période suivante selon la dynamique d’accumulation décrite par l’équation (5), dans laquelle η représente le taux de dépréciation annuel du capital :

(3)

(fonction de production[3]);

(4)

(répartition de la production entre C et I);

(5)

(accumulation du capital).

Ce modèle est du type de ceux développés depuis Ramsey (1928) et Solow (1956) qui visent à identifier les trajectoires de croissance optimales résultant de la conjugaison des préférences des agents, des possibilités techniques et de la dotation initiale en facteurs de production. Ils donnent un rôle important à la consommation comme objectif ultime de l’activité, mais le « moteur » de la croissance économique est l’accumulation du capital, celle-ci permettant, selon des modalités plus ou moins sophistiquées suivant les modèles, d’entraîner le changement technique et l’évolution des productivités.

Le taux d’actualisation optimal ρ (c’est-à-dire le coût d’opportunité du capital, ce qu’on perd en l’affectant à un usage donné) n’est autre que la productivité marginale du capital. On montre alors (Arrow et al., 1996b) qu’il respecte la relation suivante (6), où δ est le taux d’escompte social correspondant à la fonction de préférence (1), g est le taux de croissance optimal de l’économie, et où ν reflète la vitesse à laquelle l’utilité marginale de la consommation décroît lorsque le niveau de consommation augmente (un dollar rapporte une utilité moindre au riche qu’au pauvre).

(6)

avec

Cette formule fait bien apparaître que le choix du taux d’actualisation n’est pas libre, mais qu’il est endogène au modèle de croissance sous-jacent, tel qu’il est caractérisé par :

• le terme δ[4] ou « taux d’escompte social » : peu observable et souvent appelé « taux de préférence pure pour le présent » (Tppp); il est accusé de traduire une impatience pour le bien-être immédiat qui contredirait le souci des générations futures;

• le terme g ν, ou « effet richesse » : plus tangible, il indique qu’un dollar supplémentaire demain procurera moins de bien-être que ce même dollar aujourd’hui si on suppose que la croissance de la consommation sera positive mais que son utilité marginale décroît.

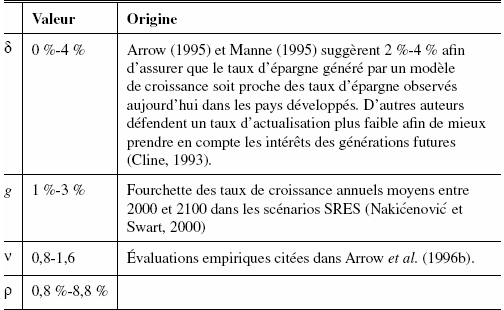
Le tableau 1 résume les principales valeurs trouvées dans la littérature pour chacun de ces paramètres, ce qui conduit à des taux d’actualisation allant de 1 % à 9 %. En fait, toutes ces valeurs ne sont pas également légitimes car toutes les combinaisons de terme δ, g et ν ne sont pas possibles si on veut calibrer un modèle réaliste.

Tableau 1

Évaluation numérique du taux d’actualisation

2. À la recherche du « bon » taux d’actualisation de long terme

2.1 Long terme : la préférence pure pour le présent est-elle légitime?

L’idée qu’il est injuste de donner aux générations futures un poids plus faible qu’aux générations présentes remonte à Ramsey, qui qualifie l’actualisation des utilités « d’indéfendable du point de vue de l’éthique » (1928 : 543). Mais Koopmans (1960) et Koopmans et al. (1964) avance un contre-argument théorique très fort. Il montre en effet que, si l’on suppose que les préférences des agents sur des plans de consommation intertemporels vérifient cinq axiomes de base[5], alors ces préférences sont de la forme (2) avec un Tppp δ > 0. Ce résultat est d’abord dû au fait que l’on cherche à ordonner tous les plans de consommation jusqu’à l’infini sans supposer une utilité bornée : il faut alors que la série des facteurs d’actualisation ∑q_t soit convergente. De plus (critère de stationnarité), le facteur d’actualisation doit décroître exponentiellement, autrement dit δ doit être constant pour éviter que le choix entre plusieurs séquences de consommation futures ne change selon la date à laquelle on les considère.

Outre cette contrainte logique, il apparaît numériquement qu’un Tppp non nul est nécessaire pour obtenir des trajectoires de croissance positives dès les premières générations (Koopmans, 1965) avec des taux d’épargne compatibles avec ceux que l’on observe aujourd’hui. Avec un Tppp nul, les modèles décrivent un schéma « d’accumulation primitive » où les générations présentes sont sacrifiées au bonheur des générations futures. De ce point de vue, la popularisation du terme de préférence pure pour le présent en lieu et place de taux d’escompte social est trompeuse puisque δ traduit tout autant une « préférence pour le non-sacrifice du présent ». Mais ceci ne rend pas pour autant illégitime les inquiétudes sur le fait que des Tppp élevés sur des horizons temporels longs ne conduisent à préempter le futur.

Pour prévenir ce risque, plusieurs alternatives ont été proposées. Un premier groupe d’articule autour de principes axiomatiques :

• le principe du maximin[6], qui prône de maximiser l’utilité de la génération la plus désavantagée. Mais introduire un tel critère dans un modèle de croissance aboutit à une croissance zéro (Solow, 1974) : tant que la croissance est positive, en effet, il est toujours possible d’augmenter le bien-être de la génération la moins bien dotée, la première, en réduisant son taux d’épargne, et l’équilibre n’est atteint que lorsque ce taux d’épargne est nul, donc lorsque la croissance est nulle[7];

• l’axiomatique de G. Chichilnisky (1996), qui montre que toutes les relations de préférences qui vérifient les deux axiomes de « non-dictature du futur » et de « non-dictature du présent » peuvent être représentées par la somme pondérée d’un critère actualisé (pas forcément à taux constant) et d’un critère qui ne dépend que de la valeur de la consommation à l’infini (2) :

(7)

avec

et Φ(c_∞) une mesure de l’utilité de la consommation

– supposée bornée – quand t tend vers l’infini.

Mais l’introduction de cette fonction dans un modèle de croissance génère des comportements problématiques. En effet, si les poids q_t sont exponentiellement décroissants, le modèle suit d’abord une trajectoire similaire à celle que l’on obtiendrait avec le seul critère actualisé, puis une trajectoire similaire à celle que l’on obtiendrait avec le seul critère « limite ». Or, cette seconde partie de la trajectoire exige une quantité de capital très élevée afin de maximiser la consommation « à la fin des temps ». Pour constituer ce capital, il faut donc passer par une phase de très forte épargne et de faible consommation[8] où les générations intermédiaires sont sacrifiées. Avec un Tppp décroissant dans le temps, le critère limite domine et le taux d’épargne s’avère très élevé dès le départ (Beltratti et al., 1996). En définitive, malgré l’introduction d’un nouveau paramètre d’arbitrage entre présent et futur (β), le problème du non-sacrifice d’une génération reste entier.

Un second ensemble de réponses vise à prendre en compte de façon plus correcte la manière dont les individus font des choix intertemporels. Les études empiriques montrent en effet que ceux-ci, placés devant des choix intertemporels, ne respectent pas les prescriptions du critère actualisé. On observe les principales « anomalies » suivantes :

• un effet de distance : le taux d’actualisation implicite est d’autant plus faible que le gain ou la perte sont éloignés dans le temps; au bout d’un certain temps en effet, même si je me préoccupe de mes descendants, la différence entre la 10^e et la 11^e génération sera forcément inférieure à celle que je fais entre mes enfants et mes petits-enfants (Schelling, 1995);

• un effet d’amplitude : des montants élevés sont actualisés à un taux plus faible que des montants faibles;

• une asymétrie pertes-gains, les gains étant actualisés à un taux plus élevé que les pertes;

• une asymétrie ralentissement-accélération : rapprocher un gain futur d’un intervalle de temps donné est moins valorisé que le fait d’éloigner ce gain d’un même intervalle de temps (Loewenstein et Prelec, 1992).

Des facteurs d’actualisation « hyperboliques » de la forme α > 0, β > 0 permettent d’intégrer une partie de ces « anomalies » et rendent mieux compte des observations empiriques sur les choix des individus (Cropper et al., 1994). Que de tels facteurs soient utiles pour étudier le comportement des agents ne fait pas de doute mais, transposés dans un modèle de croissance, ils conduisent à ce que chaque génération épargne moins que les suivantes (Phelps et Pollak, 1968)[9]. Or ceci, qui conduit à des taux d’épargne élevés pour les générations éloignées, semble contredit par l’expérience historique de baisse de ces taux sur la longue durée[10].

Pour rester dans le cadre de notre métaphore initiale, cela pose le problème des garanties selon lesquelles les générations futures respecteront bien le taux d’épargne que leur attribue le décideur. C’est pourquoi Arrow (1999) a introduit l’idée que celui-ci peut simplement faire un pari sur cette valeur; il renvoie alors à un « jeu » entre générations. Or Phelps et Pollak ont montré qu’il existe pour ce jeu un unique équilibre de Nash, caractérisé par un taux d’épargne constant σ̂, qui n’est pas, en général, Pareto-optimal. Autrement dit, il existe un taux d’épargne σ̄ > σ̂ tel que si toutes les générations l’adoptaient, toutes verraient leur utilité augmenter par rapport à un équilibre non coopératif. Mais cet équilibre est instable, car chaque génération a intérêt à adopter un comportement de passager clandestin et à reporter l’effort sur les autres.

Ainsi, le critère quasi hyperbolique (ou hyperbolique) conduit à une incohérence dynamique des choix en ce sens que des programmes mis en oeuvre peuvent se révéler ex post moins efficaces que d’autres du simple fait du passage du temps. En supposant maintenant que le planificateur bienveillant intègre les comportements (non coopératifs) attendus des générations futures[11], le critère hyperbolique aboutit alors à un taux d’épargne constant et à une trajectoire identique à celle résultant d’un critère actualisé classique. Il semble donc que, malgré l’horizon de très long terme qui caractérise le changement climatique, il convienne de conserver un critère actualisé classique, la raison principale étant que ce critère traduit une préoccupation réelle, le non-sacrifice des générations présentes et qu’aucune des alternatives examinées ne s’avère vraiment convaincante. Mais surtout, comme le montre bien l’équation (6), le Tppp est loin de dicter à lui seul le niveau du taux d’actualisation.

2.2 Taux d’actualisation et hypothèses sur la croissance[12]

On oublie parfois, quand on parle de taux d’actualisation, que celui-ci ne peut être choisi par combinaison arbitraire des trois paramètres δ, g et ν si l’on veut garder une vision cohérente du futur[13]. Calibrer par exemple un modèle avec des taux de croissance de 5 % et un Tppp de 4 % implique une hypothèse peu réaliste sur la productivité marginale du capital (9 %) capable d’assurer une croissance rapide malgré une forte préférence pour la consommation immédiate. De plus, cette forte croissance économique conduit à plus d’émissions. Les niveaux de concentration entraînant des dommages importants, s’ils existent, sont donc atteints de façon plus précoce, entraînant une progression rapide de la valeur de l’environnement et on peut très bien conclure à la nécessité d’une action rapide pour éviter d’aller « dans le mur ». Dit autrement, dans un modèle complet, il n’est pas si aisé d’écraser le long terme si celui-ci est correctement décrit.

Certes, ces garde-fous n’existent pas quand on raisonne non plus dans le cadre d’un modèle de croissance complet, mais, pour des raisons pratiques, sur la base d’une approche partielle où l’on s’interroge sur le « bon » taux à retenir pour guider les choix décentralisés. Il faut alors réintroduire ces garde-fous à plusieurs niveaux.

• La formule (6) n’implique pas a priori que le taux d’actualisation soit constant, et ceci pour deux raisons. D’abord, il convient de s’interroger sur le réalisme d’un taux de croissance de 3 % par an – à plus forte raison 5 à 6 % – maintenu sur un siècle. À contenu matière constant, ce taux conduirait à multiplier par 19 nos consommations d’énergie et matières premières. En d’autres termes, soit on explicite des mécanismes structurels de dématérialisation (mais à ce moment-là, la croissance des émissions se ralentit spontanément et le ratio entre le coût des politiques climatiques et le PIB décroît très vite), soit on envisage une saturation progressive de la croissance (vers 1 % par an) et un taux d’actualisation décroissant avec l’horizon temporel[14]. On retrouve alors une notion d’actualisation décroissante sans pour autant postuler des préférences hyperboliques.

• Weitzmann (1998) montre que les incertitudes sur les taux de croissance de long terme, dues par exemple à l’incertitude sur le progrès technique, devraient conduire à des taux d’actualisation décroissants avec l’horizon temporel considéré pour la simple raison que, plus le temps passe, plus les états du monde résultant d’un scénario de croissance faible à t + n pèsent davantage que les états du monde à la même date engendrés par une croissance forte. Une croissance forte implique en effet, de par (6), un taux d’actualisation élevé et, par conséquent, « l’écrasement » des états du monde correspondants. Une version simple de la démonstration est donnée par Newell et Pizer (2001) : la valeur actuelle de 100 $ en 2100 est de 20,28 $ si l’on actualise à 1 % et 0,20 $ si l’on actualise à 7 %; d’où, avec une probabilité de 50 % pour chaque scénario une valeur moyenne de 10,24. Si on refait le calcul pour 101 ans, on trouve 20,08 (20,28 / 1,01) et 0,19 (0,2 / 1,07) respectivement, soit une moyenne de 10,13. Or, 10,13 est proche de 10,24 / 1,01 : tout se passe comme si seul le taux d’actualisation bas comptait (adopter une hypothèse supérieure de 10 % ne changerait pas le résultat). Newell et Pizer montrent alors que traiter les taux futurs comme aléatoires autour d’une moyenne de 4 % conduit à augmenter de 80 % le coût des dommages trouvés par Nordhaus (1994) avec un taux de 4 % considéré comme certain. La raison en est, bien sûr, que lorsque les taux d’intérêt passent par des cycles bas, le futur se « dévalue » moins rapidement.

• L’impact de la dégradation de l’environnement sur la productivité des facteurs : en d’autres termes, l’investissement en biens « normaux » sera moins efficace si l’on doit renouveler plus rapidement le capital existant ou pallier une irrégularité accrue des ressources en eau. La difficulté est ici que la formule (6) n’est valide qu’à la marge d’un scénario optimal; retenir le taux de base du scénario de référence revient donc à admettre implicitement que les dommages sont marginaux. On devrait, en théorie, calculer le scénario optimal par un modèle complet incluant les dommages et leur impact sur la productivité, puis en dériver le taux d’actualisation à communiquer aux acteurs décentralisés. Or cette opération reste hasardeuse en l’état actuel des connaissances sur les dommages du changement climatique (MacCarthy et al., 2001). On ne peut donc que procéder par une correction « au doigt mouillé » qui reflète les anticipations que l’on a sur le ralentissement de la productivité générale provoqué par les impacts du changement climatique.

• L’introduction de l’environnement comme source d’aménités pour permettre d’exprimer les préférences pour le maintien de la qualité du climat « tel qu’il est ». On peut soutenir que, de même qu’au-delà d’un niveau de richesse permettant d’être comblé en biens matériels on peut « se payer le luxe » d’investir dans des tableaux de maître, de même, l’environnement est un bien « supérieur » au sens où la volonté à payer pour lui croît avec le revenu. On peut représenter cet effet en supposant que l’utilité de chaque génération, maintenant notée u(c, s), dépend à la fois de la consommation c et de la qualité de l’environnement s. Dans ce cas, la formule (6) devient (7) ci-dessous, où h est le taux de variation de la qualité de l’environnement au cours du temps, et où μ < 0 traduit le fait que, plus la richesse augmente, plus l’utilité marginale de l’environnement augmente.

(8)

avec et

Ce qui précède ne permet certes pas de définir le taux d’actualisation à choisir pour l’étude des risques climatiques puisqu’il y a autant de taux qu’il y a de visions du monde plausibles. Mais cela permet de cadrer le raisonnement et d’éliminer quelques fausses pistes, par exemple l’idée qu’il conviendrait de choisir pour taux d’actualisation public des valeurs proches du rendement actuel des portefeuilles (Lind, 1982). C’est la productivité marginale du capital qui importe telle qu’elle est mesurée sur le long terme, compte tenu de taux de croissance plausibles sur un siècle qui ne dépassent pas 3 % par an. Or, sans prétendre que ceci fournit une tendance extrapolable, notons avec Newell et Pizer (2001) que les bons à long terme du Trésor américain, s’ils ont connu de très fortes variations, font apparaître une tendance baissière qui passe de 6 à 8 % dans les années 1790-1810 à 2 à 4 % depuis 1950 (période 1978 et 1982 exceptée avec une pointe à 6 %)[15].

Si l’on considère cette dernière fourchette, et si l’on affecte à chacune de ses deux bornes une probabilité d’occurrence de 50 %, alors des dommages survenant en 2100 sont actualisés à un taux de 2,57 % en équivalent certain. Ce chiffre passe même à 1,57 % si l’on choisit une fourchette de 1 % à 3 % pour traduire l’hypothèse d’une poursuite de la tendance baissière des taux d’intérêt sur le long terme. À cela on peut rajouter, mais sans qu’on ait aujourd’hui de bases empiriques pour le faire, des modulations à la baisse pour tenir compte de la préférence pure pour l’environnement et des rétroactions négatives du changement climatique sur la productivité globale.

3. Actualisation, incertitude et décision séquentielle

Comme on vient de le voir, la détermination du taux d’actualisation de long terme ne peut se faire sans tenir compte de l’incertitude sur les scénarios de long terme. En fait, en présence d’incertitudes généralisées, portant aussi bien sur les dommages que sur le contenu du changement technique, c’est la nature même du schéma décisionnel qui doit évoluer, ce qui a de fortes implications sur le statut même du taux d’actualisation, puisqu’on va le voir, celui-ci n’est plus le seul « prix » à considérer dans le calcul intertemporel.

3.1 Incertitudes : au-delà de la maximisation de l’utilité espérée?

Classiquement, le calcul économique en univers incertain recourt au critère de maximisation de l’utilité espérée pour représenter les choix des agents :

(9)

avec p_i la probabilité de l’événement c_i .

Les fondements de ce critère, lorsque les probabilités d’occurrence des différents états du monde peuvent être évaluées statistiquement, viennent de Von Neumann et Morgenstern (1947). Lorsqu’on ne peut tirer aucune information de l’expérience passée, Savage (1951) confirme l’utilisation de ce critère en affectant à chaque état du monde une probabilité subjective d’occurrence[16]. Ceci constitue un affaiblissement des ambitions initiales, mais n’empêche pas l’utilisation du critère de l’utilité espérée en matière d’effet de serre de se heurter à trois obstacles :

• sa difficulté à rendre compte des comportements réels des agents face à des risques de faible probabilité, mais aux conséquences potentiellement larges (Allais, 1953);

• l’existence d’incertitudes dites endogènes, qui dépendent de nos décisions au lieu d’être de simples aléas de la nature : par exemple, le prix des énergies sans carbone dépend des choix antérieurs de R&D qui, eux-mêmes, dépendent de notre volonté de limiter l’effet de serre. Dans le sens inverse, la sensibilité de la réponse climatique dépend de la date à laquelle sont effectuées les baisses d’émissions ou les captures de carbone par les sols et les forêts (Gitz et Ciais, 2003). Ces incertitudes endogènes peuvent conduire à des équilibres multiples à long terme, rendant difficile l’application du schéma standard (Kreps et Porteus, 1979) puisque l’état « moyen » peut n’avoir qu’une probabilité très faible[17];

• il est difficile d’identifier tous les états du monde futurs possibles et de leur attacher une probabilité subjective (tableau 2). Certes des critères de décision ne nécessitant pas le recours aux probabilités (par exemple mini-max, mini-max regret ou principe de symétrie) peuvent être envisagés, mais ils esquivent l’un des enjeux centraux de la décision en matière d’effet de serre, à savoir la nécessité de coordonner les anticipations d’agents avec des « croyances » différentes et disposant d’informations controversées sur les risques qu’ils encourent.

Au total, les alternatives proposées au critère de maximisation de l’utilité espérée aboutissent jusqu’ici à sacrifier la cohérence temporelle des choix (le fait que le simple passage du temps ne change pas la décision optimale) (Starmer, 2000). Du point de vue de la décision publique, cela constitue une limitation rédhibitoire. C’est pourquoi, « en attendant mieux », il faut tirer tout le parti possible du critère de maximisation de l’espérance de l’utilité subjective qui permet de représenter explicitement les croyances et force à distinguer les énoncés relatifs aux états du monde futur de ceux relatifs aux préférences des agents.

Tableau 2

Probabilités par catégorie d’incertitude sur le changement climatique

3.2 Hiérarchisation de l’impact des incertitudes sur la décision de court terme

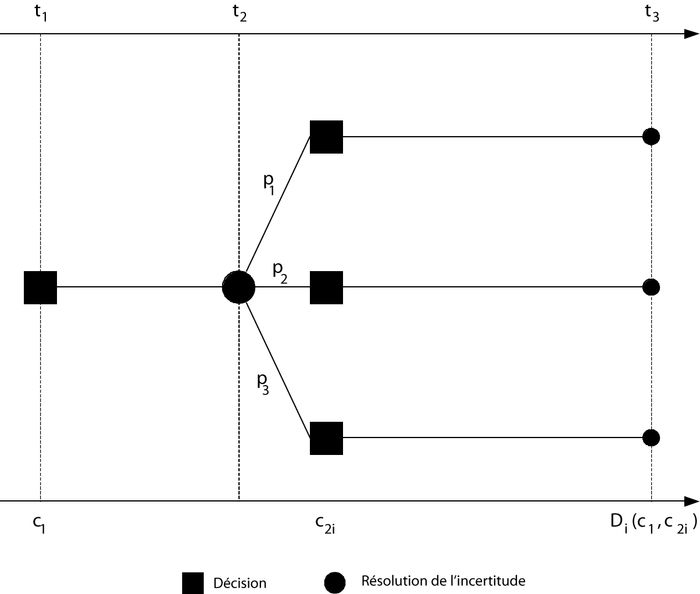
Dans un contexte de grandes incertitudes, les économistes s’accordent sur la nécessité d’un schéma de décision séquentielle (graphique 1) permettant de réviser les premières décisions en fonction de l’évolution des connaissances sur les risques et de l’expérience directe sur les coûts d’abattement. Logique du point de vue de la rationalité formelle, la séquentialité de la décision permet en outre de prendre en charge des situations où l’essentiel est de trouver un noyau d’accord entre partenaires ayant des visions du monde différentes pour laisser du temps à la résolution de leurs controverses (Hourcade, 1991; Godard, 1993). Comme l’ont très tôt exprimé A. Manne et R. Richels (1992) : « We do not need to be overly concerned by our inability to predict the detailed character of the energy system several decades into the future. Uncertainty is important only to the extend that it confounds near-term decision-making. Today’s decision appear to be relatively insensitive to some of the most controversial long-term uncertainties in the greenhouse debate ».

La différence entre calcul économique standard et décision séquentielle peut être illustrée par une métaphore automobile. Un conducteur ignore s’il va trouver une plaque de verglas dans un virage surplombant un précipice sur une route de montagne. Il lâche l’accélérateur, presse légèrement la pédale de frein, prêt à ralentir plus fortement en cas de signe de verglas ou à reprendre de la vitesse dans le cas contraire. Les risques étant trop contrastés, la distribution de probabilité trop inconnue et l’information utile risquant de venir trop tard en raison de l’inertie du véhicule, le comportement raisonnable n’est alors pas de choisir une trajectoire optimisée une fois pour toute, mais d’opter pour un processus séquentiel où les premières décisions visent à augmenter le temps d’apprentissage et à harmoniser vitesse du véhicule et arrivée de l’information (Hourcade, 1994). Pour le risque climatique, si nous agissons trop peu aujourd’hui, nous risquons de devoir freiner les émissions très brutalement demain, à coût très élevé, en cas de mauvaise surprise. À l’inverse, trop agir aujourd’hui peut être inutilement coûteux s’il s’avère que les dommages sont finalement moins graves que prévu.

Graphique 1

Note : Schéma simplifié de décision séquentielle : les carrés symbolisent les décisions et le rond central la date de levée de l’incertitude. Le processus comprend quatre étapes : l’abattement de première période, la révélation de l’état du monde, l’abattement de seconde période et, en fin de seconde période, les dommages.

Pour comprendre lequel de ces deux effets l’emporte, Ha-Duong et al. (1997) partent du fait que l’on ignore aujourd’hui lequel de ces trois plafonds de concentration atmosphérique en gaz à effet de serre, 450, 550 et 650 parties par million (ppm), il convient d’adopter. La première attitude consiste à faire un pari sur la valeur moyenne de 550 ppm. Dans ce cas (graphique 2), il n’est nul besoin de baisser fortement les émissions par rapport aux tendances en cours (trajectoire 550 cert.). Mais une attitude plus rationnelle consiste à tenir a priori ces trois cibles pour équiprobables et à faire le pari que nos connaissances vont s’améliorer au fur et à mesure du temps. Dans ce cas, et si l’on fait l’hypothèse que la « bonne » cible sera révélée en 2020, on constate que le niveau d’abattement qui minimise l’espérance mathématique des coûts est plus élevé (courbe en trait plein). En effet, les coûts du rattrapage du temps perdu en cas de mauvaise nouvelle (il faut stabiliser à 450 ppm) l’emportent sur les coûts de réductions trop précoces (la « bonne » cible est 650 ppm)[18].

Graphique 2

Note : Sentiers d’émission selon que l’on vise une concentration de 550 ppm ou que l’on suppose 450, 550 et 650 ppm équiprobables avec information révélée en 2020 ou 2035 (Ha-Duong et al., 1997).

Ce résultat se révèle en outre robuste au choix du taux d’actualisation : alors que viser 550 ppm sans tenir compte de l’incertitude conduit à des réductions en 2020 de 3 % par rapport aux émissions de référence, on trouve, en tenant compte de l’incertitude, des baisses de 9 % à 14 % selon qu’on prend un taux d’actualisation de 5 % ou 3 %. Ce modèle révèle par contre deux paramètres déterminants pour le niveau de l’action à court terme : le degré d’inertie de l’économie, c’est-à-dire sa capacité à réduire rapidement les émissions de gaz à effet de serre et la date d’arrivée de l’information. L’impact de ce dernier est illustré par la courbe en pointillée sur le graphique 2, où l’on a fait une hypothèse plus pessimiste sur la date d’arrivée de l’information (2035) et où le niveau de l’action de court terme est par conséquent plus élevé.

Cet exercice confirme que le taux d’actualisation devient un paramètre parmi d’autres, à côté de l’inertie du capital et de la valeur de l’information. L’essentiel est en effet de tenir compte de la valeur d’option d’une stratégie (Arrow et Fisher, 1974; Henry, 1974), c’est-à-dire de sa capacité à s’adapter à de nouvelles informations. Mais le raisonnement précédent souffre d’une limite qui est de prendre des cibles absolues que l’on ne peut violer alors que, dans la réalité, en cas d’action trop tardive, les sociétés accepteront un dépassement plutôt qu’un freinage à coût social trop élevé. Il y a donc une fenêtre de tir pour chaque niveau de concentration et le problème de décision est de savoir si on se donne a priori un jeu de niveaux de concentration ou si l’on cherche à évaluer les dommages attachés à chacun de ces niveaux.

Dans ce dernier cas, on quitte l’analyse coût-efficacité stochastique où les cibles résultent de choix politiques pour l’analyse coûts-bénéfices où le rôle du taux d’actualisation semble a priori décisif. On compare en effet des impacts éloignés dans le temps avec des coûts immédiats, avec risque « d’écrasement » des premiers. Cependant, on peut montrer (Lecocq, 2000) que le paramètre clé pour la décision est la forme même de la fonction dommages. Les deux graphiques ci-après – produits dans le cadre d’un modèle d’évaluation coût-bénéfice à deux périodes (cf. encadré 1) – montrent le volume optimal de réduction des émissions au cours de la première période en fonction du taux d’actualisation pour deux fonctions dommages, l’une linéaire et l’autre avec effets de seuil.

Lorsque les dommages sont linéaires, le niveau du taux d’actualisation se révèle décisif. Le graphique 3 montre en effet que le niveau optimal d’abattement en première période est élevé pour des taux d’actualisation inférieurs à 3 %, mais qu’il s’effondre pour des taux supérieurs à 5 %. On peut alors montrer que le taux d’actualisation et la pente de la fonction dommage ont un impact du même ordre de grandeur sur ce niveau. En revanche, si les dommages comportent des épisodes « à effet de seuil », leur existence et la date de leur occurrence deviennent clefs, loin devant le taux d’actualisation et l’inertie de l’économie. En effet, comme le montre le graphique 4, le niveau optimal d’abattement en première période est beaucoup moins sensible au taux d’actualisation. En d’autres termes, le futur est moins « écrasé » que ce qu’on pourrait craindre en première analyse et on voit bien que tout se joue sur l’anticipation des dommages; si les risques climatiques sont réels et si on les affecte d’une prime de risque suffisante, alors l’utilisation de la technique de l’actualisation ne conduit pas à repousser indéfiniment l’action, pourvu que les taux choisis pour le très long terme soient déterminés en tenant compte des garde-fous indiqués dans la section précédente.

Encadré 1 — Décision de première période selon la forme de la fonction dommage

Le temps est divisé en deux périodes 1 et 2 de durée n et m respectivement. Les dépenses d’abattement à chaque période sont notées c₁ et c₂, et les dommages du changement climatiques sont représentés par la fonction D(c₁, c₂). Le problème de décision est de minimiser la facture climatique totale ci-dessous, où ρ est le taux d’actualisation.

La fonction D résume à la fois les anticipations sur les coûts de réduction des émissions et les croyances sur les dommages du changement climatique. Si l’on note ψ(c₁, c₂) la concentration atmosphérique à long terme qui résulte des efforts d’abattement (c₁, c₂), et θ les dommages associés à un niveau de concentration donné, alors la fonction de dommage D peut être réécrite sous la forme :

On teste ici deux spécifications de la fonction θ. La première est linéaire dans le niveau de concentration ψ. Elle correspond à l’hypothèse selon laquelle les dommages du changement climatique se manifesteront progressivement. Dans la seconde, les dommages sont nuls en deçà d’un certain seuil de concentration, mais croissent de façon exponentielle au-delà, pour atteindre rapidement des valeurs très élevées. Cette seconde forme correspond à la possibilité que l’augmentation des concentrations déclenche, passé un certain seuil, des événements catastrophiques, comme par exemple l’arrêt de la circulation thermohaline dans l’Atlantique Nord. Lecocq (2000) calibre enfin ces deux fonctions de telle sorte qu’à l’optimum, dans un modèle coût-bénéfice complet (avec représentation explicite des dommages), les émissions optimales cumulées soient les mêmes que celles qui seraient obtenus dans un cadre coût – efficacité (avec uniquement une cible en concentration donnée a priori), avec pour cibles 450, 550, 650 et 750 ppm respectivement.

Graphique 3

Niveau d’abattement de première période en fonction du taux d’actualisation et de l’amplitude des dommages, fonction de dommages linéaire (Lecocq, 2000).

Graphique 4

Niveau d’abattement de première période en fonction du taux d’actualisation et de l’amplitude des dommages, fonction de dommages à effet de seuil (Lecocq, 2000).

En conclusion, on obtient la hiérarchie suivante pour les incertitudes. La question la plus importante est de savoir si l’on fait, ou non, l’hypothèse que des dommages « catastrophiques » sont possibles. Si oui, alors le niveau de concentration au-delà duquel ces dommages se réalisent devient le paramètre le plus important pour la décision de court terme, devant le degré d’inertie du système économique et, en troisième lieu seulement, le niveau du taux d’actualisation. Si l’on suppose au contraire que les dommages du changement climatique sont essentiellement linéaires avec la concentration, alors la valeur du taux d’actualisation, et le niveau de cette pente sont – à égalité – les deux paramètres les plus importants pour la décision de court terme, devant le degré d’inertie de l’économie (tableau 3).

Tableau 3

Hiérarchie des incertitudes pesant sur la décision de court terme en décision séquentielle

Conclusion

Nous avons essayé ici de montrer comment la prise en compte du long terme dans le calcul économique pouvait se faire, malgré les risques de mésusages, à partir du concept d’actualisation. On peut résumer en quatre points nos conclusions strictement techniques :

• le taux d’actualisation de long terme n’a de sens qu’au sein d’anticipations explicites de la croissance et dans un schéma de décision séquentielle qui permette de tenir compte de la valeur de l’information future;

• le taux à retenir pour l’étude des politiques climatiques doit tenir compte à la fois de l’incertitude sur les taux de croissance à long terme et du fait que la préservation du climat est un bien auquel on peut attacher une importance croissante au fur et à mesure que les sociétés deviennent plus riches. Il devient dès lors peu légitime d’adopter, pour les pays de l’OCDE, des taux supérieurs à 3 %;

• les controverses sur le taux d’actualisation sont secondes pour la décision de court terme, si l’on raisonne sur un jeu de plafonds ultimes de concentration inconnus ex ante. Dans ce cas, les paramètres déterminants sont la probabilité attachée au plafond le plus strict et la date d’arrivée de l’information;

• le taux d’actualisation devient en revanche un paramètre central dans le cas d’une analyse coûts – bénéfices qui valorise monétairement les dommages. Dans ce cas, l’autre paramètre clef est la forme de la fonction dommage; en présence de phases d’accélération des dommages la valeur de l’environnement croît alors assez vite pour contrebalancer « l’écrasement du futur » que produit l’actualisation.

Au-delà de ces éléments techniques, nous voudrions conclure en élargissant le débat sur l’arbitrage intertemporel. Pour protéger les générations présentes d’une dictature du futur, l’actualisation est un outil important qui n’implique pas nécessairement un sacrifice des générations futures car celui-ci dépend, en dernière instance, de la lucidité des générations présentes sur la réalité des risques. Or, des générations « lucides » n’ont pas à s’interroger seulement sur l’arbitrage à faire entre niveau de concentration et niveau de revenu, arbitrage qui est l’enjeu de l’actualisation. En effet, derrière un même niveau de revenu, elles peuvent léguer à leurs descendants plusieurs contenus qui seront déterminants pour leur liberté d’action :

• du capital installé; adopter une technologie détermine le niveau d’émissions pendant toute la durée de vie de l’équipement (30 à 50 ans pour les centrales électriques, plus pour les logements ou les infrastructures de transport). En cas d’accélération soudaine de l’action par suite d’information alarmiste, la charge de l’effort portera alors sur les seuls secteurs flexibles (industrie) ou sur la consommation courante (Lecocq et al., 1998);

• un stock de R&D : Gerlagh et Van der Zwaan (2001) montrent que prendre en compte l’induction du progrès technique conduit à doubler le niveau d’investissement optimal sur les énergies renouvelables (R. Tol pousse à l’extrême le raisonnement dans une parabole résumée dans l’encadré 2). Or, l’effort de recherche global dans le domaine de l’énergie s’est considérablement affaibli au cours de la dernière décennie (Edmonds et al., 2000).

L’enjeu consiste ici à prévenir des situations de verrouillage technologique dans des sentiers intensifs en carbone (Arrow et al., 1996a), comme ceux résultant de la quasi-disparition du fret transport et de villes où la mobilité ne peut être assurée que par la voiture individuelle. Signalons par exemple que la moitié du futur parc immobilier de la Chine en 2015 reste à construire (World Bank, 2002). Le choix de telle ou telle trajectoire dépend donc de décisions en des domaines qui ne seront qu’en partie déterminées par les taux d’actualisation public. Une actualisation raisonnée représente donc un progrès pour clarifier les débats sur le tempo des réponses vis-à-vis des risques climatiques et pour harmoniser les politiques publiques entre secteurs; mais la prise en compte des valeurs d’option pour intégrer les incertitudes sur le futur passera par bien d’autres variables de commande que le seul coût du capital.

Encadré 2 — La parabole de Richard Tol

Tol (1998) considère un monde dans lequel la génération actuelle souhaite que la concentration atmosphérique en CO₂ ne dépasse jamais un plafond relativement bas. Mais que les générations futures peuvent avoir un avis différent sur la question et se laisser aller à un plafond plus élevé.

Si la génération actuelle ne tient pas compte de ce risque, la politique optimale à court terme se caractérise alors par une trajectoire d’abattement relativement « douce » et une faible quantité de R&D. En supposant que chaque génération a 10 % de chances d’être « laxiste », il conclue que le pourcentage chance de stabiliser les concentrations au niveau souhaité par la première génération n’est que de 13 %.

Supposons maintenant que la génération présente intègre ce risque; elle doit alors adopter une politique climatique plus agressive. Pour s’assurer une probabilité finale de 40 %, Tol calcule qu’elle doit augmenter ses abattements (de 2 % à 6 % environ des émissions de référence en 2020), mais surtout multiplier par un facteur 10 les investissements en R&D afin « d’inciter » ainsi les générations futures à abattre davantage en modifiant les termes de leur analyse coûts bénéfices.

Notes

• [1] Un classique de la critique de l’usage du taux d’actualisation en matière d’effet de serre est Cline (1993).
• [2] Cette métaphore conduit aux mêmes résultats que la métaphore du marché parfait; mais celle du planificateur est plus aisée pour notre propos.
• [3] On peut utiliser une fonction de production quelconque. On choisit ici une fonction de Cobb-Douglas parce qu’on peut en tirer aisément quelques propositions simples faisant apparaître des liaisons fondamentales entre paramètres.
• [4] Par contre, le fait de donner à δ une valeur particulière véhicule un choix normatif fort : par exemple, Manne (1995) recommande δ entre 2 % et 4 % afin de faire en sorte que les taux d’épargnes optimaux restent proches de leurs valeurs actuelles.
• [5] Complétude, continuité, sensibilité à la première période, non-complémentarité des consommations sur deux périodes successives, stationnarité et existence d’extrema.
• [6] Ce critère traduit l’analyse des principes de la justice distributive selon Rawls (1971), c’est-à-dire ceux que concevraient des personnes libres et rationnelles gouvernées par leur intérêt personnel si elles devaient décider des règles et institutions qui encadrent leur vie sociale en étant derrière un « voile de l’ignorance », c’est-à-dire dans l’ignorance de leurs capacités, de leurs conceptions du bien, de leur position dans la société et du niveau de développement de la société dont elles seront membres. Rawls conclut que, placé dans cette situation, ces personnes choisiraient de maximiser le bien-être de l’individu le plus désavantagé.
• [7] Claude Henry (2000) montre qu’une croissance positive peut être obtenue avec un critère mini-max si chaque génération est suffisamment altruiste, au sens où son utilité dépend aussi de l’utilité de la génération suivante.
• [8] La date de cette transition dépend de la valeur du paramètre β.
• [9] Phelps et Pollak raisonnent sur des coefficients « quasi hyperboliques » de la forme q₀ = 1, pour t > 0, avec 0 < β < 1 et 0 < δ. Les résultats qu’ils obtiennent sont applicables aux coefficients hyperboliques.
• [10] Homer et Sylla (1996), ayant recomposé les taux d’intérêt depuis le 11^e siècle montrent une baisse continue depuis le 17^e siècle avec une fourchette de 4,5 % à 12 %, qui passe à 2 %-6 % au 20^e siècle.
• [11] Robert Solow se montre ici sceptique : « Leaving aside all technical points, I have to say this does not feel anything like the way policy is talked about or could be talked about in a democracy, especially since any current generation is notoriously bad at guessing what future generations will want or do » (1999).
• [12] Cette section s’inspire en particulier de Heal (2001).
• [13] Cette vision cohérente doit bien sûr, dans le cas qui nous occupe, incorporer les incertitudes sur le futur et ne se confond pas avec la définition du scénario le plus probable.
• [14] Newell et Pizer (2001) aboutissent à un résultat similaire en prolongeant la tendance à la baisse des taux de rendement des bons du Trésor américain.
• [15] Ceci rejoint les ordres de grandeurs fournis par Homer et Sylla (1996), cf. note de bas de page 12.
• [16] Le lecteur trouvera chez Luce et Raiffa (1957) un exposé complet des théorèmes de Von Neumann et Morgenstern et de Savage.
• [17] Par exemple, dans une étude systématique des paniers technologiques susceptibles d’être engendrés sur le très long terme, en tenant compte des mécanismes d’apprentissage qui font qu’une technologie à d’autant plus de chance de s’imposer qu’on lui a consacré d’efforts, Gritsevskyi et Nakićenović (2000) font apparaître clairement des discontinuités dans la distribution des probabilités avec accumulations autour des paniers très intensifs en carbone, traduisant une dominance des effets d’apprentissages sur les technologies charbon, et autour des paniers peu émetteurs en carbone, traduisant une prise en compte précoce des risques climatiques. La densité de probabilité est au contraire très faible pour des « paniers moyens ». Il y a là une figure de choix entre deux lock-in technologiques.
• [18] Gollier et al. (2000) identifient les conditions analytiques dans lesquelles l’un des deux effets l’emporte sur l’autre, sur la base d’un modèle simple d’accumulation de la pollution sur deux périodes.