Abstracts
Résumé
Il existe une perception qu’il y a des inégalités économiques entre les générations et plus précisément que la situation économique des jeunes travailleurs d’aujourd’hui est moins bonne que celle de leurs aînés. Dans ce texte, on cherche à tester cette hypothèse pour les hommes et les femmes au Canada. En combinant des microdonnées des recensements canadiens de 1971, 1981, 1986, 1991 et 1996, on estime des régressions de gains qui isolent les effets de l’année de naissance et de l’âge. Les valeurs monétaires sont converties avec l’indice des prix à la consommation (IPC). Dans la spécification de base, il n’y a pas d’autres variables explicatives. Pour les hommes, on obtient le résultat que la génération la plus « chanceuse » est celle née en 1944 et que les moins fortunés sont ceux nés récemment. Pour les femmes, la génération ayant les gains les plus élevés est celle née en 1960 et les générations récentes gagnent beaucoup plus que les plus anciennes. L’inclusion de variables explicatives standards ne change pas la forme de la relation entre les gains et l’année de naissance, mais les écarts entre générations sont plus petits. Les résultats sont sensibles à l’utilisation de l’IPC pour convertir les revenus. Si on suppose, comme certains le pensent, que l’IPC a systématiquement surestimé les augmentations de prix dans le passé, la situation économique des jeunes générations est meilleure que ce qu’on aurait estimé autrement. L’inclusion de variables d’interaction entre l’âge et l’année de naissance montre que les rendements selon l’âge sont plus petits pour les générations récentes que pour les générations anciennes. Les résultats confirment en partie certaines idées courantes sur le bien-être relatif des générations, mais ils montrent aussi la difficulté de comparer les niveaux de vie dans le temps.
Abstract
There exists a perception of economic inequalities among generations and more precisely that today’s younger generations are facing worse economic conditions than those who preceded them. In this paper, this hypothesis is tested for men and women in Canada. By pooling micro-data from the Canadian censuses of 1971, 1981, 1986, 1991 and 1996, earnings regressions are estimated to isolate the effects of birth year and age. Monetary values are converted using the Consumer Price Index (CPI). In the base specification, there are no other explanatory variables. For men, it is found that the “luckiest” generation is the one born in 1944 and that the least fortunate are those born recently. For women, the generation with the highest earnings is the one born in 1960 and the recent generations earn a lot more than the earlier ones. The inclusion of standard explanatory variable does not change the shape of the relationship between earnings and birth year, but the differences among generations are smaller. The results are sensitive to the use of the CPI to convert incomes. If it is assumed, as claimed by some, that the CPI systematically overestimated price increases in the past, the economic position of the younger generations is better than estimated otherwise. The inclusion of interaction terms between age and year of birth shows that the returns to age are lower for the recent generations than for the older ones. The results partly confirm some current ideas about the relative well-being of generations, but they also show the difficulty of comparing living standards over time.
Article body
On peut changer de classe sociale, de langue, de confession religieuse ou d’état civil, on peut s’exiler de son pays natal, on peut même, à la rigueur, échanger ou transformer la culture que l’on a reçue, mais contre son âge et la date de sa naissance, on ne peut rien.
François Ricard, 1992, page 12
Introduction
Cette étude porte sur les conflits entre générations, ou plutôt sur la perception courante que des personnes nées à des moments précis dans le passé ont été plus ou moins bien servies que d’autres par la vie. On retrouve cette perception à différentes époques et dans diverses sociétés, mais on l’a observée en particulier dans les dernières années chez les jeunes qui pensent avoir eu plus de difficultés à s’intégrer à la société que leurs aînés. Par exemple, alors qu’auparavant il était normal pour une personne commençant sa vie active d’accéder à un poste à temps plein bien rémunéré et de le garder toute sa vie, plusieurs jeunes travailleurs de nos jours doivent se contenter d’emplois précaires et mal payés. Des groupes de jeunes s’opposent par exemple aux clauses dites « orphelin » que l’on retrouve dans certaines conventions collectives qui font que les nouveaux arrivés ont des échelles de salaires plus basses que les plus anciens.
L’idée qu’il y a des inégalités entre les générations est familière dans l’opinion publique et on la retrouve souvent dans la littérature, à la fois populaire et scientifique. Elle peut découler du comportement normal des groupes de pressions et de la tendance naturelle à « trouver l’herbe plus verte chez le voisin », mais dans toute opinion populaire il y a un fond de vérité. Un essai qui a connu beaucoup de succès au Québec il y a quelques années est le livre de François Ricard (1992) La génération lyrique : essai sur la vie et l’oeuvre des premiers-nés du baby-boom, (dont un extrait est cité plus haut). L’auteur soutient que les premiers-nés du baby-boom, ceux nés entre la fin de la Deuxième Guerre et le début des années cinquante, ont été choyés par la vie sur tous les plans, que ce soit économique, social ou culturel. Dans tout ce qu’ils ont voulu faire, les membres de cette génération avaient les portes grandes ouvertes devant eux. Les autres générations ont eu moins de chance, celles qui sont arrivées avant parce qu’elles ont dû vivre la grande dépression et la guerre et celles qui sont arrivées après parce que les premiers-nés du baby-boom avaient déjà pris toute la place. L’auteur de cet essai appartient au monde de la littérature et pas à celui des sciences sociales, et d’ailleurs son livre ne contient aucun chiffre. Mais il est bien documenté et ses arguments sont convaincants. Dans la littérature plus « scientifique », il y a l’ouvrage classique de Richard Easterlin (1980) Birth and Fortune: The Impact of Numbers on Personal Welfare qui défend la thèse que ceux qui font partie d’une cohorte d’âges nombreuse font face à plus de difficultés durant toute leur vie, à cause de la concurrence entre membres de cette cohorte, que ceux qui font partie d’une cohorte peu nombreuse.
Une étude récente de Beaudry et Green (2000) a examiné les revenus de cohortes de travailleurs canadiens en combinant les données des différentes Enquêtes sur les finances des consommateurs au cours de la période 1971-1993. Sachant que les cohortes récentes ont été défavorisées par rapport aux cohortes plus anciennes, les auteurs cherchent à voir si ce désavantage initial des jeunes cohortes est susceptible d’être compensé par des rendements à l’expérience plus élevés. Ils arrivent à la conclusion que ce n’est pas le cas. La présente étude se rapproche un peu de celle de Beaudry et Green, mais pose une question différente. L’objectif est de mesurer l’ordre de grandeur sur l’ensemble du cycle de vie des écarts salariaux entre les cohortes de travailleurs. On propose une méthode pour estimer ces écarts et on teste la sensibilité des résultats à certaines hypothèses. On fait abstraction initialement des différences dans les rendements de l’expérience, mais la question est abordée plus tard dans l’analyse.
L’objectif de cette étude est donc de vérifier si cette perception d’inégalités entre générations est vraie, en se basant principalement sur une variable, soit le revenu salarial. Cette variable ne mesure pas évidemment l’ensemble du bien-être d’une personne, mais elle en est une composante importante qui a l’avantage de se mesurer facilement[1]. On veut savoir si les personnes nées à une certaine époque vont gagner plus ou moins que d’autres au cours de leur cycle de vie. Pour répondre à cette question, il faudrait en principe avoir des profils de revenus d’individus nés à différents moments en fonction de leur âge que l’on observerait sur toute leur vie et que l’on pourrait comparer entre eux. Les données idéales n’existent pas. Certaines données longitudinales permettraient ce genre d’analyse, mais la plupart ne vont pas suffisamment loin en arrière pour examiner les revenus passés de générations plus anciennes qui sont toujours actives ou qui ont récemment quitté le marché du travail. Il y a aussi le problème qu’on ne connaît pas encore les revenus que les générations plus jeunes auront dans le reste de leur vie.
On ne peut donc pas répondre précisément à la question mais on peut faire des estimations. Cette étude essaie d’aborder la question en tenant compte du problème des données. En l’absence de données longitudinales, on peut observer des « groupes » de différents âges à différents moments dans le temps, c’est-à-dire des « cohortes synthétiques ». En l’absence de profils complets de revenus par âge de toutes les générations d’individus, on peut utiliser des données sur les revenus de ces générations pendant une période assez longue pour estimer des profils généraux selon l’âge. C’est ce qu’on fait dans cette étude avec les données de cinq recensements canadiens couvrant une période d’un quart de siècle.
La première section décrit les données utilisées, introduit un modèle de base pour la relation entre gains et année de naissance et présente les principaux résultats. Ces résultats sont conformes à certaines idées courantes sur le bien-être relatif de diverses générations. Les autres sections cherchent à tester la validité des résultats principaux. Dans la deuxième section, on ajoute au modèle d’autres variables pouvant expliquer les revenus qui sont habituellement incluses dans les études empiriques sur le capital humain. Dans la troisième section, on cherche à savoir comment les résultats sont affectés par le choix de l’indice de prix qu’on utilise pour comparer les revenus à différents moments. On montre que ceux-ci sont assez sensibles aux hypothèses sur l’indice de prix. Dans la quatrième section, on considère une variante du modèle de base où la variable dépendante est le revenu total. La cinquième section aborde la question de la différence dans les rendements de l’âge selon les générations. La sixième section conclut cette étude.
1. Données et spécification du modèle de base
Cette étude utilise les microdonnées des particuliers de cinq recensements canadiens, soit ceux de 1971, 1981, 1986, 1991 et 1996. L’avantage principal de ces données par rapport à d’autres est qu’elles couvrent une longue période, soit 25 ans, ce qui permet de voir des tendances à assez long terme. Un autre avantage est que les échantillons sont grands. Seulement les personnes âgées de 25 à 64 ans sont sélectionnées et les hommes et les femmes sont analysés séparément. La variable de revenu utilisée est les traitements et salaires annuels durant l’année précédant le recensement et seules les personnes ayant déclaré des traitements et salaires positifs sont considérées. Les données de tous ces recensements sont réunies en une seule grande base[2]. Dans la spécification initiale, les valeurs monétaires de revenus sont converties en dollars de 1995 avec l’indice des prix à la consommation (IPC). À la troisième section, on revient sur cette hypothèse.
La combinaison de plusieurs recensements a pour but de distinguer les effets de l’année de naissance et de l’âge sur le revenu. Avec les données d’un seul recensement, il y a évidemment une corrélation parfaite entre ces deux variables et on ne peut pas estimer séparément leurs effets. La plupart des études qui estiment des régressions de gains avec des données de coupe instantanée interprètent les résultats comme indiquant un effet de l’âge ou de l’expérience, suite en grande partie aux études de Mincer. Mais comme la littérature sur l’immigration l’a montré à l’instigation de Borjas (1985), cela revient à supposer que les cohortes d’individus nées à différents moments ont la même fonction de gains. La recherche a montré que ce n’était pas le cas pour les immigrants et cela est peut-être aussi vrai pour la population en général si des générations de travailleurs ont mieux réussi que d’autres. Il s’agit de l’hypothèse qu’on cherche à tester dans ce texte.
La spécification du modèle est une régression de gains de la forme :
où ln y est le logarithme naturel des traitements et salaires d’une personne en dollars constants de 1995, f est une fonction qui reste à spécifier, N est l’année de naissance (sous la forme 1900 + N), A est l’âge mesuré en années, P est un effet de période relié au cycle économique et X est un vecteur de caractéristiques individuelles. Les valeurs de A sont comprises entre 25 et 64 en fonction du choix de l’échantillon. Comme dans le recensement de 1971 les personnes les plus vieilles sont nées en 1907 (= 1971 – 64) et que dans celui de 1996 les personnes les plus jeunes sont nées en 1971 (= 1996 – 25), les données nous permettent d’observer des personnes nées sur une période de 65 ans (= 1971 – 1907). Cependant, la quantité d’information qu’on a sur chaque génération est limitée par le fait que les recensements ne couvrent qu’une période totale de 25 ans. Plus une génération est ancienne ou plus elle est récente, moins souvent on l’observe. Le tableau 1 indique les recensements dans lesquels les générations sont observées. Les personnes nées entre 1932 et 1946 sont observées cinq fois, alors que les autres sont observées moins souvent. Si on considère comme fiables les données des générations observées dans au moins trois recensements, on couvre les années de naissance 1922-1961, ce qui est une assez longue période. Par ailleurs, les résultats pour les années de naissance observées seulement une ou deux fois (1907-1921 et 1962-1971) sont probablement moins exacts et il faudra garder cela à l’esprit.
Tableau 1
Correspondance entre année de naissance par période de 5 ans et observation dans les recensements canadiens pour les personnes âgées de 25 à 64 ans
Dans le premier stade de l’analyse, seulement l’âge et l’année de naissance sont inclus du côté droit de l’équation; P est omis et X ne comprend qu’un terme constant. Normalement, les régressions de gains de ce type comprennent des variables telles l’éducation, le statut matrimonial, les heures travaillées, la région, etc. Celles-ci seront ajoutées dans une étape ultérieure. La spécification adoptée ici peut être vue comme une forme réduite pure, dans le sens qu’une personne peut choisir son niveau d’éducation, ses heures ou son type de travail, mais elle ne peut rien contre son année de naissance et son âge. Les résultats indiqueront donc l’effet sur les gains d’appartenir à une génération et un groupe d’âge, indépendamment de tout ce qu’une personne a à sa disposition ou peut faire pour améliorer son sort. Le modèle est estimé séparément pour les hommes et les femmes, la variable de sexe pouvant aussi être vue comme un attribut purement exogène.
Il reste à spécifier la forme fonctionnelle de f . L’approche ici est d’être éclectique, tout en imposant certaines restrictions. La littérature adopte fréquemment une fonction quadratique pour la relation entre le revenu et l’âge (ou l’expérience); celle-ci donne de bons résultats car il y a une relation concave entre le revenu et l’expérience. A priori, on ne fait pas d’hypothèse sur la relation entre revenu et année de naissance. La fonction f est spécifiée comme étant un polynôme en N et en A d’un degré assez grand pour permettre une certaine flexibilité. Des polynômes de degrés jusqu’à 6 ont été estimés. En pratique, un polynôme de degré 5 semble suffisant et la régression estimée est donc :
On note que la forme fonctionnelle est additive pour les termes en N et A. L’absence de termes d’interactions revient à supposer qu’il y a un profil de revenu de base par âge qui est le même pour tout le monde, mais que celui-ci peut être plus ou moins élevé dépendant de l’année de naissance. Cette hypothèse est restrictive et on y reviendra à la cinquième section. On sait que chaque génération fait face à des événements qui peuvent influencer l’évolution de ses revenus. Les générations plus âgées qui ont vécu la grande dépression et la guerre ont sûrement été affectées par ces circonstances, mais nos données ne le montrent pas car elles commencent en 1971. Il en est de même des générations plus jeunes dont on ne connaît pas l’avenir. On utilise cette forme fonctionnelle pour faciliter l’interprétation des résultats et à cause de la disponibilité des données. Si on permettait à chaque génération d’avoir un profil de revenu par âge différent, il faudrait estimer l’ensemble de ces profils pour comparer les générations entre elles en fonction de critères à définir, tels la valeur présente de leurs gains sur toute leur vie. Comme on ne suit pas les générations à tous les âges mais à 5 moments durant une période de seulement 25 ans, on ne peut pas observer ces profils au complet. On pourrait sûrement les estimer, mais au prix de certaines hypothèses elles aussi restrictives. Dans les circonstances, l’hypothèse retenue ici a l’avantage de la simplicité car elle revient à estimer un profil par âge « moyen » à partir des observations que l’on a sur toutes les générations.
Ce qui nous intéresse est principalement la forme de la relation entre ln y et N. On veut savoir en particulier si cette relation atteint un maximum pour une certaine année de naissance, c’est-à-dire si une génération est plus « chanceuse » que les autres. On veut savoir aussi quels sont les écarts entre les gains à ce maximum et ceux aux autres générations. Un intérêt secondaire est aussi la relation entre ln y et A. Les régressions complètes sont aux tableaux A1 et A2 de l’annexe. Les coefficients de régressions comme tels ne nous informent pas directement sur la nature de ces relations. L’analyse sera faite en termes de graphiques, où on considère ces deux relations aux valeurs moyennes des autres variables.
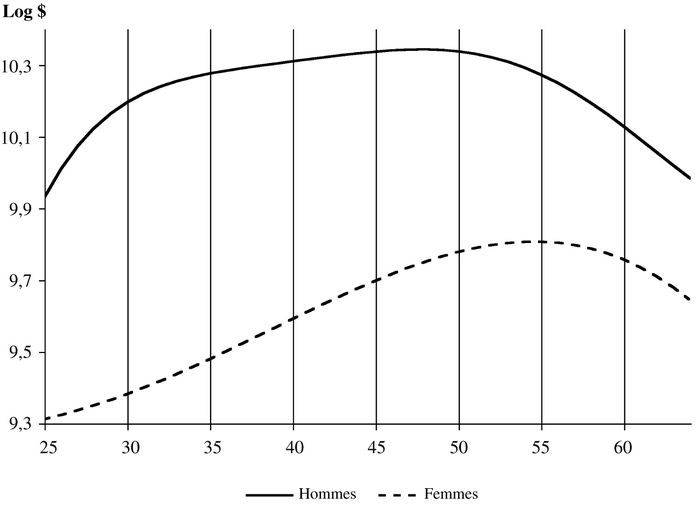
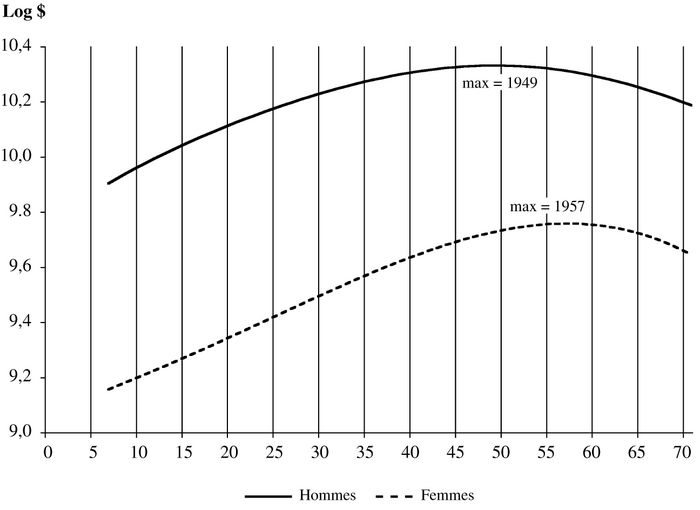
Le graphique 1 montre les résultats de l’estimation du modèle de base décrit ci-dessus. Ce graphique et les suivants ont tous la même forme. Dans la partie a, on illustre la relation estimée entre les gains et l’année de naissance pour les hommes et les femmes séparément; dans la partie b, on fait la même chose pour la relation entre les gains et l’âge.
Graphique 1
Modèle de base, sans variables de contrôle, correction avec l’IPC
a
Relation entre gains et année de naissance
b
Relation entre gains et âge
Si on considère la relation entre gains et année de naissance pour les hommes, on note que celle-ci atteint un maximum pour l’année 1944, ce qui est très près de l’hypothèse notée plus haut que la génération la plus « chanceuse » serait celle des premiers-nés du baby-boom. Le graphique montre aussi que les hommes qui s’en tirent le moins bien sont ceux des générations les plus jeunes. On note que les hommes nés à partir du milieu des années soixante ont des gains plus bas que tous ceux qui les ont précédés, y compris ceux nés dans les premières décennies du vingtième siècle. Ceci peut paraître surprenant compte tenu du fait que les jeunes générations sont censées avoir vécu dans des conditions beaucoup meilleures que celles de leurs grands-parents. Mais ces résultats sont cohérents avec l’observation de la baisse des revenus réels à long terme.
On a une situation très différente pour les femmes. La relation entre gains et année de naissance atteint un maximum pour l’année 1960 et les femmes nées dans les décennies récentes gagnent beaucoup plus que leurs aînées du début du siècle. Cette situation s’explique, non pas par le baby-boom, mais par les changements qui se sont produits dans le marché du travail des femmes au cours des dernières décennies, à savoir l’augmentation du taux d’activité et la progression des salaires. Cependant, le graphique montre un léger déclin après 1960. Il y a donc peut-être des facteurs, tels la détérioration des conditions du marché du travail, qui agissent de la même façon pour les femmes que pour les hommes.
La différence entre la courbe des hommes et celle des femmes indique l’écart de gains entre les deux sexes selon les générations. Même si les femmes de toutes les générations gagnent moins que leur contrepartie masculine, on peut voir que l’écart entre les deux sexes s’est considérablement amoindri pour les générations les plus jeunes.
La partie b du graphique montre la relation entre les gains et l’âge. Même si cette relation n’est pas l’objet principal de cette étude, il faut quand même l’examiner pour vérifier la validité du modèle car les deux relations sont estimées à partir des mêmes données. On obtient la forme concave attendue, à savoir que les gains augmentent avec l’âge à un taux décroissant. Les gains des hommes plafonnent à un âge relativement bas, moins de 50 ans, et ceux des âges les plus avancés redescendent aux niveaux de ceux des âges les plus bas. Cela est un peu surprenant et il est possible que les données ne permettent pas de distinguer complètement les effets des différents facteurs et que l’effet d’une certaine baisse à long terme du pouvoir d’achat soit capté par la variable âge. Par ailleurs, pour les femmes, le profil des gains par âge se rapproche plus de celui attendu, dans la mesure où les gains plafonnent à un âge plus élevé et que ceux des femmes âgées ne descendent pas aussi bas que celles qui débutent leur carrière. Dans les autres hypothèses du modèle discutées plus bas, la forme concave de la relation entre gains et âge demeure, quoique avec quelques variations. Cela est une indication de la validité du modèle. Dans l’analyse qui suit, on ne discutera plus de la relation entre gains et âge pour se concentrer sur celle entre gains et année de naissance.
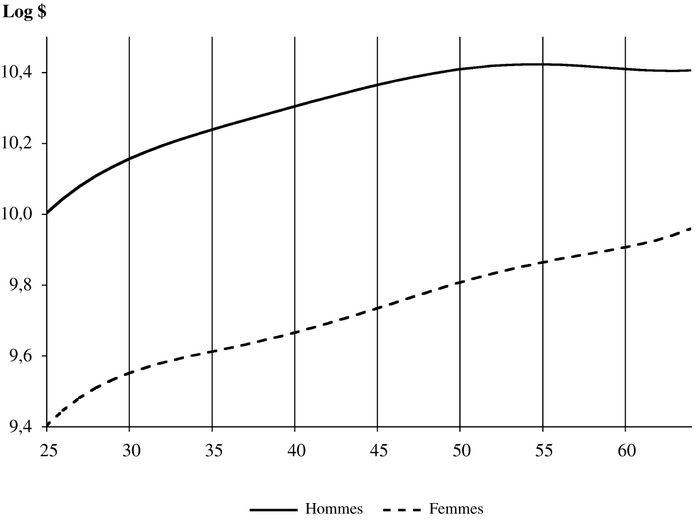
Le graphique 2 reprend la même analyse mais se limite aux personnes à temps plein qui ont travaillé toute l’année[3]. On élimine donc les écarts de gains dus aux différences dans le temps passé au travail. Les niveaux de gains sont évidemment plus élevés que dans le graphique 1 et les écarts entre les hommes et les femmes sont plus petits. Pour toutes les générations et particulièrement les plus anciennes, les gains plus faibles des femmes observés dans le premier graphique sont en grande partie dus au fait que celles-ci travaillent moins de semaines et d’heures que les hommes. Les écarts entre générations pour les travailleurs à temps plein toute l’année sont plus petits et les générations récentes d’hommes gagnent plus que les générations nées au début du siècle, contrairement à ce qu’on avait au graphique 1. Il semble donc qu’un facteur important relié à la baisse des revenus des jeunes générations d’hommes soit relié à la réduction du temps de travail.
Les résultats jusqu’ici confirment jusqu’à un certain point ce à quoi on s’attendait étant donné ce qu’on connaît sur l’évolution du marché du travail et la société en général. Dans le reste du texte, on va chercher à vérifier si les résultats sont robustes et s’ils peuvent être expliqués par des facteurs observables[4].
2. Effet de période et variables explicatives
Les régressions qui combinent plusieurs coupes instantanées incluent couramment des effets fixes reliés à la période. Il faut noter cependant qu’il y a par définition une multicolinéarité parfaite entre les trois variables d’âge, d’année de naissance et de période, et qu’on ne peut donc pas identifier tous les effets de ces variables. Comme cette étude s’intéresse aux profils de gains selon l’année de naissance et l’âge, on a choisi de laisser ces effets varier librement selon la forme fonctionnelle présentée plus haut et de contraindre l’effet de période. Notons que cet effet est introduit pour tenir compte du fait que les cinq observations correspondant aux années de recensement peuvent correspondre à des moments différents du cycle économique. On peut donc le définir en fonction de ce que l’on connaît de l’évolution de l’économie canadienne durant la période étudiée. Les décennies des années quatre-vingt et quatre-vingt-dix se caractérisent toutes les deux par la présence d’une forte récession dans leur première moitié et par une reprise par la suite. Les années d’observation 1980 et 1990 se situent juste avant une récession et correspondent à un taux de chômage relativement bas. L’année 1970 est aussi une année à bas chômage qui se situe avant une récession, quoique moins forte que celles des décennies subséquentes. Par ailleurs, les années 1985 et 1995 se situent juste après le début de la reprise alors que le chômage est en baisse mais encore relativement élevé. En fonction de cette analyse sommaire, les cinq années d’observations peuvent se diviser en deux groupes, soit les années 1970, 1980 et 1990 d’une part, et les années 1985 et 1995 d’autre part[5]. Une variable dichotomique correspondant à ces groupes est donc ajoutée pour tenir compte de l’effet de période.
Graphique 2
Modèle de base, personnes à temps plein toute l’année, sans variables de contrôle, correction avec l’IPC
a
Relation entre gains et année de naissance
b
Relation entre gains et âge
Les régressions de gains habituelles comprennent aussi d’autres variables explicatives que celles retenues jusqu’ici. Le vecteur X de l’équation présentée plus haut comprend maintenant des variables de contrôle pour le nombre d’années de scolarité, le statut matrimonial, la région de résidence, le nombre de semaines travaillées et le nombre d’heures travaillées. La liste de ces variables est présentée au début de l’annexe. Elle est limitée par l’information disponible dans chacun des cinq recensements utilisés, mais elle comprend les principaux facteurs que les auteurs incluent habituellement.
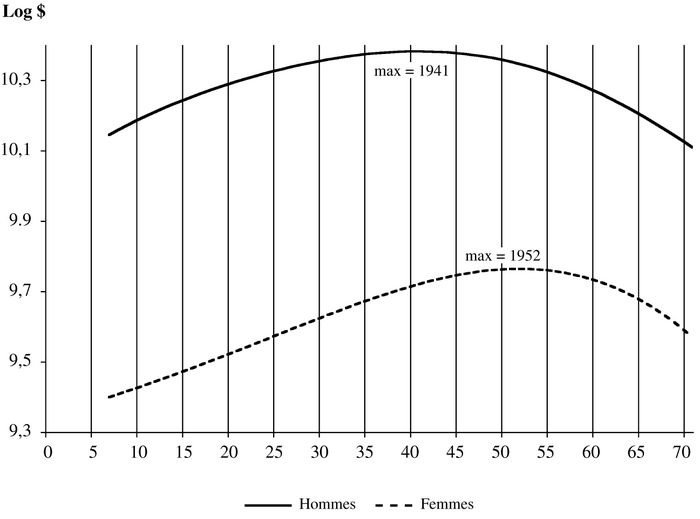
Les régressions de la troisième colonne des tableaux A1 et A2 de l’annexe montrent que les variables de contrôle ont les effets attendus et on n’en discutera pas plus longuement. On note en particulier que les deux années à chômage élevé, soit 1985 et 1995, correspondent à une diminution de gains de 5,4 % pour les hommes et de 4 % pour les femmes. Le graphique 3 montre les relations entre gains et année de naissance, et entre gains et âge après avoir tenu compte de l’effet de période et des variables de contrôle. On voit que la relation entre gains et année de naissance a la même forme que celle du graphique 1, mais que les maximums ont lieu pour des générations plus anciennes. Les hommes les plus chanceux sont ceux nés en 1941 et les femmes les plus chanceuses sont celles nées en 1952. Ce résultat peut s’expliquer en partie par le rôle de la variable d’éducation. On sait que les jeunes générations ont eu accès à une plus grande éducation que les plus anciennes. Malgré cela, elles réussissent moins bien que ces dernières. Cela a pour effet de faire paraître encore moins bien les jeunes générations et à repousser plus loin dans le passé la génération ayant les gains les plus élevés. D’autre part, l’écart logarithmique entre le maximum et les extrémités se réduit lorsqu’on inclut des variables explicatives (sauf pour les femmes des jeunes générations). Ceci indique que les extrêmes ont moins des autres attributs qui augmentent le revenu, notamment les heures et semaines travaillées.
On peut se demander laquelle des deux relations il faut préférer, celle sans variables explicatives ou celle avec variables explicatives. Habituellement, les chercheurs utilisent les variables explicatives pour calculer des « effets nets » d’appartenir à certains groupes (ici, à des générations) par rapport à des « effets bruts ». Il y a en général une préférence parmi les chercheurs pour les effets nets car ils font abstraction des autres facteurs pris en compte. Mais dans le contexte particulier de cette étude, il n’est pas si évident que les effets nets soient les plus importants à considérer. Comme on l’a déjà mentionné, les seules variables totalement exogènes du modèle sont l’année de naissance, l’âge et le sexe. Tout le reste résulte de choix individuels ou collectifs, du moins en partie. Ainsi, certaines générations ont eu accès à des services d’éducation meilleurs que d’autres et leurs membres en ont profité pour acquérir une scolarité plus élevée. Les politiques d’éducation qui ont eu cours sont les résultats de choix qui ont affecté les jeunes à différentes époques. En contrôlant pour l’éducation, on se trouve à annuler l’effet de ce facteur. Il en est de même des conditions changeantes du marché du travail qui font en sortes que certains groupes à différentes époques ont travaillé plus ou moins d’heures ou de semaines. Dans la mesure où l’objectif est de comparer le bien-être relatif des différentes générations, on ne veut pas nécessairement annuler l’effet des circonstances qui ont affecté les différentes générations. Dans ce contexte, l’effet brut qui ne tient compte que de l’âge et du sexe est peut-être le plus pertinent. Quoi qu’il en soit, le lecteur est libre de choisir l’interprétation qu’il préfère.
Graphique 3
Modèle avec variables de contrôle, correction avec l’IPC
a
Relation entre gains et année de naissance
b
Relation entre gains et âge
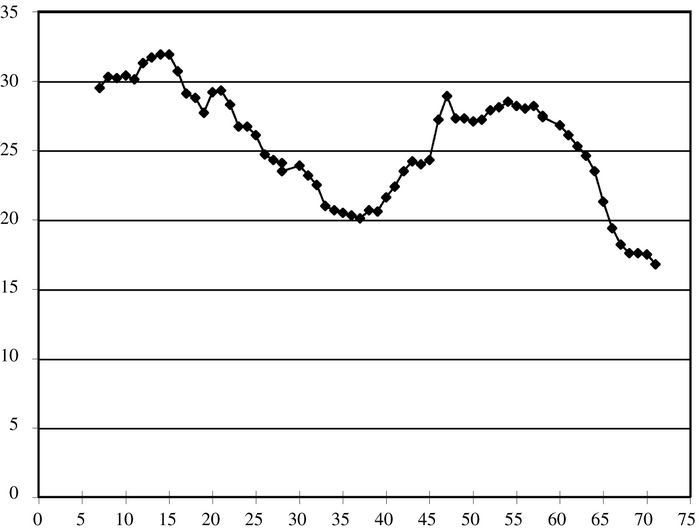
Une autre variable qui peut avoir un effet est la natalité et la taille de la cohorte. Depuis les travaux pionniers de Easterlin (1980), on a essayé de relier l’évolution à long terme de la performance économique des générations à l’évolution de la natalité. Le graphique 4 montre le taux de natalité canadien entre les années 1907 et 1971, soit pour les mêmes générations que celles considérées dans cette étude. Le taux de natalité a connu beaucoup de fluctuations. Il a été bas durant la grande dépression et la guerre. Il a ensuite grimpé fortement pour engendrer ce qu’on a appelé le baby-boom. Depuis le début des années soixante, le taux de natalité a fortement diminué. Indépendamment de ces fluctuations, il y a une tendance à la baisse de la natalité durant toute la période. Selon Easterlin, les membres des générations moins nombreuses, soit celles nées quand le taux de natalité était bas, ont plus de facilité durant toute leur vie parce qu’ils font face à moins de concurrence de leur propre génération.
Une inspection visuelle des graphiques montre que la thèse d’Easterlin peut avoir du sens, mais seulement pour les hommes nés jusqu’au baby-boom approximativement. En effet, le statut économique des hommes nés dans les quatre premières décennies du vingtième siècle s’améliore à mesure que la natalité baisse. Lorsque la natalité se remet à augmenter avec le baby-boom, le statut économique commence à se détériorer, mais pas nécessairement au même moment. Cependant, les hommes nés dans les années soixante ont des revenus bas, malgré le fait que le taux de natalité était faible lorsqu’ils sont nés, contrairement à ce que la thèse prédit. Dans le cas des femmes, il n’y pas vraiment de relation avec la natalité. Leur statut économique s’est continuellement amélioré malgré la hausse et ensuite la baisse de la natalité. En fait, celles qui s’en tirent le mieux sont nées une époque où la natalité était élevée[6].
Graphique 4
Taux de natalité (/1000), Canada, 1907-1971
3. Sensibilité des résultats aux choix de l’indice de prix
Lorsqu’on compare des revenus à différents moments dans le temps, il faut rendre les valeurs monétaires en dollars constants. L’indice des prix à la consommation (IPC) utilisé ici est un indice couramment accepté pour faire ces comparaisons. Cependant, les indices de prix sont sujets à erreurs et il faut se demander comment ces erreurs affectent les résultats de l’analyse. Dans des comparaisons sur de courtes périodes, des petites erreurs dans l’estimation de l’indice de prix n’ont probablement pas trop de conséquences. Mais ce n’est pas le cas ici car les données portent sur une période de 25 ans et que l’effet cumulatif de petites erreurs peut devenir assez grand[7].
Il existe une certaine littérature qui a montré que l’IPC avait tendance à être biaisé à la hausse, c’est-à-dire qu’il tend à surestimer les augmentations de prix. Il y a plusieurs raisons à cela[8]. Un type de biais est celui lié à la substitution de produits étant donné que l’IPC mesure le prix d’un panier fixe de biens alors que les consommateurs vont chercher à modifier leur panier de consommation en fonction des changements de prix relatifs. Pour pallier ce problème, le panier de biens de l’IPC est régulièrement modifié, mais on ne peut pas le faire aussi vite que les consommateurs changent leurs habitudes d’achats. Il y a aussi un biais causé par l’arrivée de nouveaux produits. Plusieurs produits à haute technologie coûtent cher à leur arrivée sur le marché mais leurs prix baissent par la suite. Ces nouveaux produits ne sont introduits dans le panier de l’IPC qu’après un certain temps, lorsqu’ils deviennent des éléments assez importants de la consommation et que leurs prix ont déjà baissé. Un autre type de biais est celui relié aux substitutions de points de vente. Par exemple, des magasins à grandes surfaces offrent des produits à rabais comparativement aux commerçants traditionnels et les observations de prix faites pour l’IPC ne tiennent pas toujours correctement compte des changements des points de vente[9]. L’IPC peut aussi surestimer des hausses de prix s’il ne tient pas suffisamment compte des améliorations de la qualité de certains produits.
Il est évidemment difficile d’évaluer l’importance exacte de ces biais quoiqu’il y ait généralement consensus que l’IPC surestime les augmentations de prix. Aux États-Unis, une étude qui a fait du bruit est ce qu’on a appelé le « Rapport Boskin » (Boskin et al., 1996, 1997). Cette étude a évalué l’ensemble de ces biais et a conclu que l’IPC américain surestimait le changement du coût de la vie d’environ 1,1 % par année. Il s’agit d’un biais assez important puisqu’il s’accumule à chaque année. On a essayé de voir si ce résultat était valable pour d’autres pays, dont le Canada. Crawford (1998) a évalué les différents biais pour le Canada et est arrivé à la conclusion que le biais total était plus faible qu’aux États-Unis. Il estime le biais à environ 0,5 % par année. Les raisons semblent être reliées au fait que Statistique Canada fait un meilleur travail que son homologue américain dans l’estimation des changements de prix, entre autres que les paniers de biens de consommation sont révisés plus souvent.
Dans le contexte de cette étude, les conséquences peuvent être assez importantes si l’IPC a surestimé les augmentations de prix étant donné l’effet cumulatif potentiel sur 25 années. Ceci veut dire que le pouvoir d’achat des revenus gagnés récemment est plus grand par rapport au revenu gagné dans le passé que les montants en dollars constants calculés avec l’IPC ne le montrent. Une conséquence est que la situation économique des jeunes générations dont on a estimé que les revenus étaient faibles est peut-être meilleure qu’on ne le pensait après tout. Pour vérifier cela, on a réestimé le modèle en corrigeant différemment pour les variations de prix à travers le temps, soit en supposant une surestimation de 0,5 % par année, qui est la valeur retenue par Crawford pour le Canada.
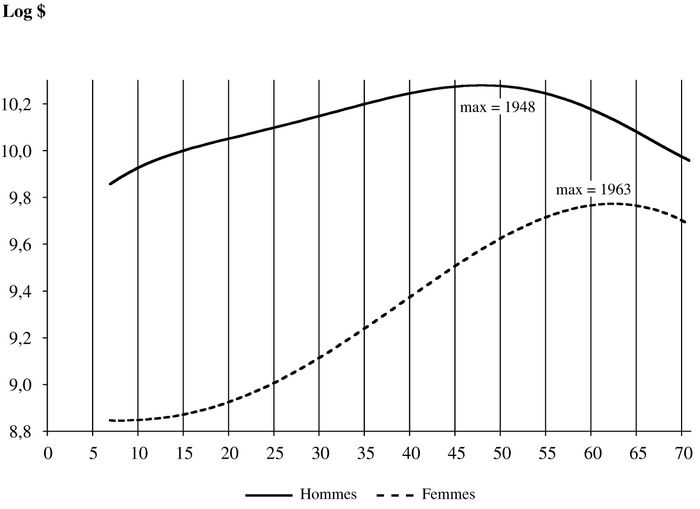
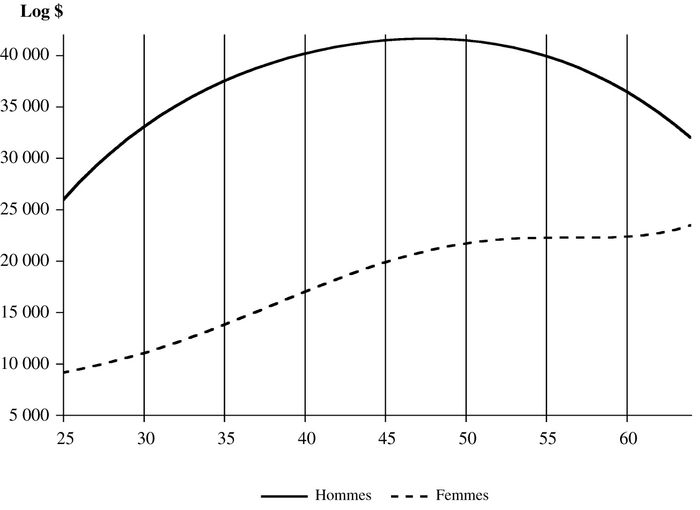
Le graphique 5 présente les résultats avec cette hypothèse et sans variables de contrôle. Il y a des changements assez importants par rapport au modèle de base du graphique 1. On voit effectivement que les jeunes générations s’en tirent mieux lorsqu’on fait cette hypothèse. Pour les hommes, les gains maximums sont atteints pour la génération de 1948 (au lieu de celle de 1944 dans le graphique 1) et l’écart entre cette génération et les suivantes est beaucoup plus faible. De plus, les gains des jeunes générations sont plus élevés que ceux des générations du début du siècle, contrairement à ce qu’on avait auparavant. On a un résultat semblable pour les femmes où le maximum est atteint à l’année 1963. L’écart entre celles-ci et celles des générations plus anciennes est aussi augmenté lorsqu’on fait cet ajustement à l’indice de prix.
Dans un sens, ces résultats sont peut-être plus conformes à nos attentes étant donné la croissance économique du vingtième siècle. Même si on sait que les jeunes ont de la difficulté de nos jours, il est difficile de croire qu’ils s’en tirent beaucoup moins bien que les personnes nées au début du siècle, qui ont vécu à des époques où la productivité était beaucoup moindre qu’aujourd’hui et où la vie était difficile. Donc, cette étude corrobore peut-être l’hypothèse que l’IPC a mal estimé les augmentations de prix et que notre bien-être aujourd’hui est plus élevé que ce qu’il ne l’était auparavant.
Enfin, le graphique 6 refait l’analyse des graphiques précédents en incluant les variables de contrôle. Les résultats sont semblables. L’hypothèse que l’IPC surestime les augmentations de prix a pour conséquence de déplacer la valeur maximum des gains vers des années de naissance plus récentes et de réduire l’écart pour les jeunes générations[10].
Dans l’ensemble, cette section montre que les comparaisons de bien-être relatifs des différentes générations sont sensibles aux hypothèses que l’on fait sur les indices de prix. Comme on ne sait pas vraiment jusqu’à quel point les indices de prix officiels sont biaisés, on ne peut pas non plus être catégorique à savoir quelles générations sont les plus fortunées.
Graphique 5
Estimation sous l’hypothèse que l’IPC surestime l’inflation de 0,5 % par année, sans variables de contrôle
a
Relation entre gains et année de naissance
b
Relation entre gains et âge
Graphique 6
Estimation sous l’hypothèse que l’IPC surestime l’inflation de 0,5 % par année, avec variables de contrôle
a
Relation entre gains et année de naissance
b
Relation entre gains et âge
4. Revenu total comme variable dépendante
Toute l’analyse jusqu’ici a été faite en termes d’une seule variable, soit les traitements et salaires. Cependant, le bien-être d’une personne dépend également des autres sources de revenus. Il est donc intéressant de vérifier si la relation obtenue s’applique à ces autres sources. Pour cela, on a réestimé le modèle en utilisant le revenu total (avant impôt), qui inclut toutes les sources y compris les transferts de l’État. De plus, toutes les personnes sont incluses, qu’elles aient déclaré un revenu total positif, nul ou négatif, et la variable dépendante est le revenu exprimé en dollars de 1995[11]. L’échantillon de la présente analyse est donc plus grand que celui qu’on avait précédemment qui ne comprenait que les personnes ayant déclaré des traitements et salaires positifs. Pour cette analyse, on utilise à nouveau l’IPC sans correction pour comparer les revenus à différentes années et il n’y a pas de variables de contrôle.
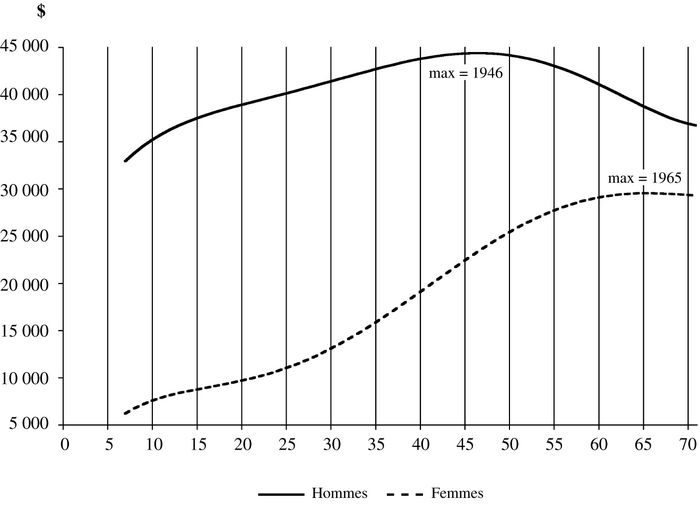
Les résultats sont présentés dans le graphique 7[12]. On obtient une relation ayant une forme tout à fait semblable à ce qu’on avait précédemment. Pour les hommes, la relation entre gains et année de naissance atteint un maximum à l’année 1946, ce qui est très près de ce qu’on avait au graphique 1. Cependant, la différence la plus importante est que le revenu total des jeunes générations est plus élevé que celui des générations du début du siècle, contrairement à ce qu’on avait auparavant avec l’IPC sans correction. Il semblerait donc que les autres types de revenus, principalement les transferts, aient atténué les pertes des jeunes générations. Celles-ci ayant vécu à une époque où il y avait une plus grande redistribution des revenus, leur situation malencontreuse a pu être corrigée jusqu’à un certain point. Cependant, l’analyse est faite avec les revenus avant impôt et les paiements de transferts sont financés par les impôts. Dans la mesure où les impôts sont progressifs, on peut penser que les jeunes générations à gains plus faibles en ont payé moins que les autres. Les impôts ont aussi servi à financer des services publics tels la santé et l’éducation qui ont profité aux générations plus récentes. Donc, dans l’ensemble, même si une évaluation globale des effets de la fiscalité et des transferts sur chaque génération est complexe et va au-delà des objectifs de cette étude, on peut quand même dire que les jeunes générations semblent avoir profité de l’intervention des gouvernements dans l’économie.
Graphique 7
Estimation avec le revenu total comme variable dépendante, sans variables de contrôle, en dollars de 1995 corrigés avec l’IPC
a
Relation entre gains et année de naissance
b
Relation entre gains et âge
5. Interaction entre âge et année de naissance
L’hypothèse de l’absence de termes d’interaction entre l’âge et l’année de naissance est restrictive et il faut l’aborder. Les résultats jusqu’à maintenant nous disent ce que serait la situation de diverses générations dans la situation « hypothétique » où les variations selon l’âge seraient les mêmes pour tout le monde. Cette façon de procéder permet de séparer les profils entre gains et année de naissance de ceux entre gains et âge. Cependant, il demeure possible que des changements dans les rendements dans l’âge entre les générations affectent leur situation et il faut en tenir compte. Beaudry et Green (2000) ont cherché précisément à tester cette hypothèse en essayant d’évaluer si les faibles revenus des générations les plus récentes étaient compensés par des rendements plus élevés à l’expérience plus tard dans leur vie.
On a ajouté des termes d’interaction entre année de naissance et âge dans la régression de gains définie à la section 1 ci-dessus. La présence de ces termes ne permet plus de tracer les courbes comme on l’a fait[13], mais par contre les coefficients des variables d’interaction nous informent sur les changements des profils par âge selon l’année de naissance, ou vice-versa. Dans une première spécification, on inclut la variable N × A de façon linéaire. Le coefficient du terme d’interaction sera positif ou négatif selon que le rendement selon l’âge pour les générations nées plus tard sera plus grand ou plus petit. Dans une deuxième spécification, on ajoute le terme au carré (N × A)2 qui permet de voir si le rendement selon l’âge varie à un taux plus ou moins grand en fonction de l’année de naissance. Les résultats sont estimés pour les régressions de gains, sans et avec variables de contrôle, et en ajustant les valeurs monétaires avec l’IPC d’une part et avec l’IPC corrigée de 0,5 % par année d’autre part, comme on l’a fait auparavant[14].
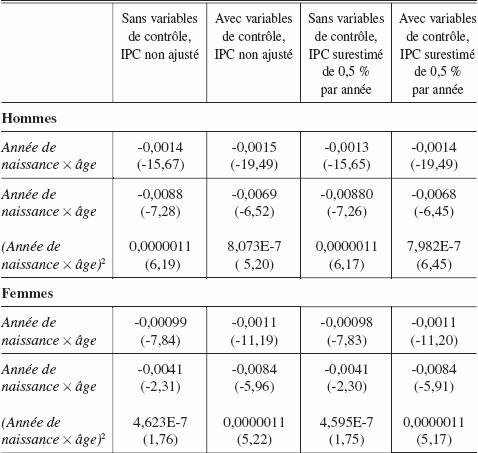
Les coefficients des variables d’interaction sont présentés au tableau 2. Ce qui ressort le plus fortement est que les effets d’interaction sont tous négatifs, ce qui veut dire que les rendements selon l’âge des générations récentes sont plus petits que ceux des générations plus anciennes. Cette conclusion est conforme à celle de Beaudry et Green (2000). Pour les hommes, selon la spécification linéaire du terme d’interaction, l’effet sur les gains d’un changement d’une année dans la variable âge diminue de 0,14 % pour chaque accroissement d’une année de naissance dans le cas où il n’y a pas de variables de contrôle. Avec des variables de contrôle, l’effet est légèrement plus élevé. Pour les femmes, le coefficient est aussi négatif mais l’effet est un peu plus faible, soit 0,10 % dans le cas où il n’y a pas de variables de contrôle et 0,11 % avec variables de contrôle. On note que les résultats sont presque les mêmes quand on fait l’hypothèse que l’IPC surestime les augmentations de prix. Ceci peut justifier qu’on ignore ce problème lorsqu’on s’intéresse seulement aux pentes des fonctions de gains. Enfin, les spécifications qui incluent le carré du terme d’interaction montrent que l’effet négatif s’atténue un peu pour les générations récentes.
Tableau 2
Coefficients d’interaction entre année de naissance et âge dans les régressions de gains
Note : Les chiffres entre parenthèses sont les statistiques t. Pour les régressions sans variables de contrôle, les autres variables de la régression incluent seulement l’année de naissance et l’âge jusqu’à la puissance cinq respectivement. Les régressions avec variables de contrôle incluent toutes les variables dans la liste des tableaux A1 et A2 en annexe.
Dans l’ensemble, cette dernière analyse montre que la situation des jeunes générations non seulement ne serait pas améliorée si on tenait compte des rendements selon l’âge différents, mais qu’elle serait aggravée. Beaudry et Green (2000) ont obtenu un résultat semblable avec une méthodologie et des données différentes. Évidemment, les données les plus récentes de cette étude sont pour l’année 1995 et il est possible que la situation change dans l’avenir pour les générations plus jeunes.
Conclusion
Les résultats de cette étude sont conformes en partie avec certaines idées courantes qu’on peut avoir sur le bien-être relatif des générations. Ils sont intéressants dans la mesure où ils fournissent une confirmation objective de ce que certains pensent. Dans le cas des hommes, les générations les plus comblées semblent être celles du début du baby-boom, comme François Ricard et d’autres l’ont suggéré. Les générations d’hommes les plus jeunes gagnent moins que toutes celles qui les ont précédées. Cependant, l’écart par rapport aux autres générations diminue lorsqu’on tient compte des heures travaillées et du biais de l’IPC. Les transferts de l’État semblent aussi avoir profité aux plus jeunes. Le cas des femmes est très différent. Il y a eu des changements considérables dans la société qui font que celles nées dans les années soixante gagnent plus que les autres. Cependant, il semble y avoir eu épuisement dans les progrès des femmes et les générations plus récentes ont peut-être été affectées.
Certains commentaires et réserves sont pertinents par rapport aux résultats de cette étude. D’abord, il faut signaler que les résultats reflètent l’évolution de la situation de l’ensemble du marché du travail au Canada et qu’ils ne s’appliquent pas nécessairement à tous les domaines d’activité. Ainsi, certaines professions peuvent avoir évolué différemment de l’ensemble et les jeunes qui y entrent peuvent réussir mieux que dans d’autres ou que dans la même profession dans le passé. Par exemple, dans le domaine du sport professionnel, il y a eu une inflation salariale telle que ceux qui sont dans la profession maintenant ont des revenus beaucoup plus élevés que ceux qui y étaient dans les décennies précédentes. Il s’agit sans doute d’un domaine un peu exceptionnel, mais il est possible qu’on ait des situations semblables dans d’autres professions. Deuxièmement, on ne sait pas comment évolueront les revenus des générations plus jeunes qui ont encore devant elles plusieurs années de vie active. Il est possible, et certains le souhaitent, que leurs revenus futurs soient plus élevés que leur situation de départ ne le prédit. Seul l’avenir nous le dira. Enfin, les résultats sont sensibles aux hypothèses sur l’indice de prix, ce qui reflète une difficulté inhérente à comparer le bien-être dans le temps. Si l’indice des prix à la consommation a systématiquement surestimé dans le passé les augmentations de prix, la situation de jeunes d’aujourd’hui n’est pas si mauvaise par rapport à celle de leurs aînés. Il faut aussi garder à l’esprit que l’analyse est faite en termes de revenus et ignore d’autres aspects du bien-être matériel des individus. Par exemple, il y a eu plusieurs innovations dans le domaine de l’informatique et les ordinateurs qu’on utilisait dans les années soixante et soixante-dix sont « archaïques » par rapport à ceux d’aujourd’hui. Les personnes qui utilisent les ordinateurs aujourd’hui, qui sont en grande partie des jeunes, tirent une plus grande jouissance de l’usage de ce bien que celles qui le faisaient dans le passé et cela n’est pas entièrement pris en compte dans les indices de prix.
Concernant les implications en termes de politiques économiques, il demeure quand même, malgré les réserves exprimées, que cette étude montre que les jeunes d’aujourd’hui, et peut-être principalement les hommes, ont beaucoup de difficultés à bien s’intégrer au marché du travail. Ce n’est pas la première étude qui suggère une telle conclusion. Des politiques visant venir en aide aux jeunes, dans les domaines de l’éducation, de la formation professionnelle et du soutien au revenu, sont donc toujours appropriées.
Appendices
Annexe
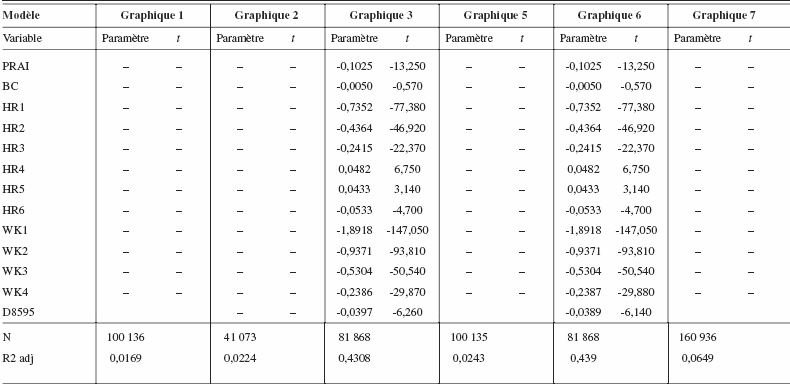
Régressions ayant servi à construire les graphiques du texte
Définitions des variables
AGE, AGE2, AGE3, AGE4, AGE5 : âge à la puissance 1 à 5 respectivement
ANNÉE, ANNÉE2, ANNÉE3, ANNÉE4, ANNÉE5 : année de naissance (moins 1900) à la puissance 1 à 5 respectivement
EDUC, EDUC2, EDUC3 : années d’éducation à la puissance 1 à 3 respectivement
Statut matrimonial (référence : jamais marié)
MARIÉ |
= 1 si présentement marié (ou vivant en union libre), = 0 autrement |
DIV-SÉP |
= 1 si présentement divorcé ou séparé, = 0 autrement |
Région (référence : Ontario)
ATL |
= 1 si résident de l’une des provinces de l’Atlantique, = 0 autrement |
QUEBEC |
= 1 si résident du Québec, = 0 autrement |
PRAI |
= 1 si résident des provinces des Prairies, = 0 autrement |
BC |
= 1 si résident de la Colombie Britannique, = 0 autrement |
Heures travaillées durant la semaine de référence (référence : 40-44 heures)
HR1 |
= 1 pour 1-19 heures, = 0 autrement |
HR2 |
= 1 pour 20-29 heures, = 0 autrement |
HR3 |
= 1 pour 30-34 heures, = 0 autrement |
HR4 |
= 1 pour 35-39 heures, = 0 autrement |
HR5 |
= 1 pour 45-59 heures, = 0 autrement |
HR6 |
= 1 pour plus de 50 heures, = 0 autrement |
Semaines travaillées durant l’année précédent le recensement (référence : 49-52 semaines)
WK1 |
= 1 pour 1-13 semaines, = 0 autrement |
WK2 |
= 1 pour 14-26 semaines, = 0 autrement |
WK3 |
= 1 pour 27-39 semaines, = 0 autrement |
WK4 |
= 1 pour 40-48 semaines, = 0 autrement |
Effet de période
D8595 |
= 1 pour recensement de 1986 ou 1996, = 0 autrement |
Tableau A1
Régressions ayant servi à construire les graphiques du texte, hommes
Tableau A2
Régressions ayant servi à construire les graphiques du texte, femmes
Remerciements
L’auteur remercie Dmitry Kabrelyan pour son travail d’assistance à la recherche. Cette recherche a été présentée à un séminaire à Statistique Canada et au Congrès de la Société canadienne de science économique. L’auteur remercie les participants de même que Bernard Fortin et Pierre Fortin pour leurs commentaires pertinents. Les erreurs et omissions sont évidemment celles de l’auteur.
Notes
-
[1]
Pierre Fortin (2002), dans une chronique du magazine L’Actualité, s’est aussi intéressé à cette question. En plus des salaires, il considère les taux de chômage des membres des différentes générations.
-
[2]
Étant donné la taille de cette base, un échantillon aléatoire est tiré de chaque recensement. Pour le recensement de 1971, on a pris 20 % des données disponibles (qui constituent 1 % de l’ensemble de la population). Pour les autres recensements, on a pris 10 % des données disponibles (qui constituent entre 2 % et 3 % de l’ensemble de la population dépendant du recensement). Pour les hommes, l’échantillon retenu comprend plus de 128 000 observations et celui des femmes en comprend plus de 100 000.
-
[3]
Ces personnes sont définies comme étant celles qui ont travaillé 48 semaines ou plus durant l’année précédant le recensement et 35 heures ou plus durant la semaine précédant le recensement.
-
[4]
D’autres analyses non illustrées disponibles auprès de l’auteur montrent qu’ils sont robustes par rapport à différents changements dans l’échantillon. Ainsi, l’analyse a été refaite à tour de rôle pour les travailleurs nés au Canada seulement et pour les résidents de différentes régions canadiennes. Les principales conclusions demeurent les mêmes.
-
[5]
Notons que le taux de chômage au Canada était de 5,7 % en 1970, 7,5 % en 1980, 10,5 % en 1985, 8,1 % en 1990 et 9,5 % en 1995 (Série Cansim D44950).
-
[6]
Le taux de natalité a été inclus dans une régression avec les autres variables explicatives, mais il n’était pas significatif. Cette régression est disponible auprès de l’auteur.
-
[7]
Curieusement, la recherche sur les comparaisons de revenus dans le temps ne s’est pas beaucoup préoccupée du problème de la fiabilité des indices de prix. Dans une étude américaine, Slesnick (2000) fait état de ce problème et utilise d’autres indices de prix pour comparer les niveaux de vie. Il conclut que l’utilisation de l’IPC a sous-estimé la croissance des niveaux de vie et surestimé les seuils de pauvreté.
-
[8]
Pour une analyse détaillée sur ces types de biais, voir Ducharme (1997).
-
[9]
Une étude récente du biais de substitution de point de vente est faite par White (2000).
-
[10]
On note en passant dans les tableaux A1 et A2 que les coefficients des variables de contrôle sont presque identiques que l’on tienne compte ou nom du biais de l’IPC. Ceci montre que ce biais n’est pas un problème si on ne s’intéresse qu’aux pentes des fonctions de gains, ce qui n’est pas le cas ici car on compare les niveaux de gains entre les générations.
-
[11]
Les travailleurs autonomes peuvent avoir un revenu négatif. À cause des valeurs négatives ou nulles, la variable dépendante pour cette analyse est exprimée en valeurs monétaires et non pas en logarithmes.
-
[12]
Il s’agit de résultats de régressions de moindres carrés ordinaires (MCO). Comme il y a beaucoup de revenus nuls, on a aussi estimé le modèle par la méthode Tobit. Pour les hommes, les résultats sont presque identiques à ceux des MCO. Pour les femmes, la méthode Tobit prédit des revenus négatifs pour les générations anciennes, ce qui fait que l’écart entre les générations récentes et anciennes est plus grand que celui estimé par la méthode des MCO.
-
[13]
On pourrait tracer la relation par rapport à une variable en supposant l’autre variable donnée, par exemple, en prenant sa moyenne. En fait, la procédure utilisée qui exclut des termes d’interaction revient à faire cela car elle calcule des profils « moyens » selon l’âge et l’année de naissance.
-
[14]
Il s’agit des régressions correspondant, sauf pour les termes d’interaction, à celles qui ont servi aux graphiques 1, 3, 5 et 6 respectivement. Les résultats complets de ces régressions sont disponibles auprès de l’auteur.
Bibliographie
- Beaudry, Paul et David A. Green (2000), « Cohort Patterns in Canadian Earnings: Assessing the Role of Skill Premia and Inequality Trends », Canadian Journal of Economics / Revue canadienne d’économique, 33(4) : 907-989.
- Borjas, George J. (1985), « Assimilation, Changes in Cohort Quality, and the Earnings of Immigrants », Journal of Labor Economics, 3 : 463-489.
- Boskin, Michael J., Ellen R. Dulberger, Robert J. Gordon, Zvi Grilichez et Dale W. Jorgenson (1996), Toward a More Accurate Measure of the Cost of Living, Final Report to the Senate Finance Committee From the Advisory Commission to Study the Consumer Price Index, Washington, D.C., Senate Finance Committee.
- Boskin, Michael J., Ellen R. Dulberger, Robert J. Gordon, Zvi Grilichez et Dale W. Jorgenson (1997), « The CPI Commission: Findings and Recommendations », American Economic Review, Papers and Proceedings, 87(2) : 78-83.
- Crawford, Allan (1998), « Le point sur les biais de mesure inhérents à l’IPC canadien », Revue de la Banque du Canada : 39-56.
- Ducharme, Louis Marc (1997), « L’IPC canadien et la question des biais : le présent et l’avenir », Biais de l’IPC : les expériences de cinq pays de l’OCDE (sous la direction de Louis Marc Ducharme), Statistique Canada, Division des prix, catalogue 62F0014MIB, p. 13-24.
- Easterlin, Richard A. (1980), Birth and Fortune: The Impact of Numbers on Personal Welfare, Basic Books, New York, 205 pages.
- Fortin, Pierre (2002), « Générations XX et XY », L’Actualité, 1er juin 2002, p. 102.
- Ricard, François (1992), La génération lyrique : essai sur la vie et l’oeuvre des premiers-nés du baby-boom, Les Éditions du Boréal, Montréal, 282 pages.
- Slesnick, Daniel T. (2000), Living Standards in the United States: A Consumption-Based Approach, The AEI Press, Washington, D.C., 55 pages.
- Urquhart, M.C. et K.A.H. Buckley (1965), Historical Statistics of Canada, Toronto, Macmillan Company of Canada.
- White, Alan G. (2000), « Outlet Types and the Canadian Consumer Price Index », Canadian Journal of Economics / Revue canadienne d’économique, 33(2) : 488-505.
List of figures
a
Relation entre gains et année de naissance
b
Relation entre gains et âge
Graphique 2
Modèle de base, personnes à temps plein toute l’année, sans variables de contrôle, correction avec l’IPC
a
Relation entre gains et année de naissance
b
Relation entre gains et âge
a
Relation entre gains et année de naissance
b
Relation entre gains et âge
Graphique 4
Taux de natalité (/1000), Canada, 1907-1971
Graphique 5
Estimation sous l’hypothèse que l’IPC surestime l’inflation de 0,5 % par année, sans variables de contrôle
a
Relation entre gains et année de naissance
b
Relation entre gains et âge
Graphique 6
Estimation sous l’hypothèse que l’IPC surestime l’inflation de 0,5 % par année, avec variables de contrôle
a
Relation entre gains et année de naissance
b
Relation entre gains et âge
Graphique 7
Estimation avec le revenu total comme variable dépendante, sans variables de contrôle, en dollars de 1995 corrigés avec l’IPC
a
Relation entre gains et année de naissance
b
Relation entre gains et âge
List of tables
Tableau 1
Correspondance entre année de naissance par période de 5 ans et observation dans les recensements canadiens pour les personnes âgées de 25 à 64 ans
Tableau 2
Coefficients d’interaction entre année de naissance et âge dans les régressions de gains
Note : Les chiffres entre parenthèses sont les statistiques t. Pour les régressions sans variables de contrôle, les autres variables de la régression incluent seulement l’année de naissance et l’âge jusqu’à la puissance cinq respectivement. Les régressions avec variables de contrôle incluent toutes les variables dans la liste des tableaux A1 et A2 en annexe.
Tableau A1
Régressions ayant servi à construire les graphiques du texte, hommes
Tableau A2
Régressions ayant servi à construire les graphiques du texte, femmes