Article body

1. Introduction

Le phosphore est un élément essentiel à l’écosystème. Dans les écosystèmes aquatiques, le phosphore est présent sous forme dissoute, particulaire et sédimentaire (LIU et al., 2016a; ZUO et al., 2016). Quelle que soit la forme considérée, il y est présent sous forme de phosphore minéral et de phosphore organique. Le phosphore organique, correspondant à des molécules de phosphates associées à des molécules à base carbonée, représente la forme dominante dans les eaux de surface. Quant au phosphore minéral, il correspond aux polyphosphates minéraux d'une part, et les orthophosphates (HnPO43-n) représentant sa forme la plus importante et la seule soluble à être utilisé par les organismes aquatiques (CAO et al., 2016; LIU et al., 2016b) d’autre part.

Si le phosphore constitue l’un des éléments nutritifs majeurs pour les écosystèmes aquatiques, il n’en demeure pas moins que sa présence excessive dans ces entités est l’une des causes principales de l’eutrophisation. Dans ce fléau écologique, il est incriminé en tant que cofacteur limitant avec l’azote (GOODY et al., 2016; KASPERSEN et al., 2016; ROLLAND et al., 2015; ULRICH et al., 2016). Il en est le facteur de maîtrise du fait de son cycle biogéochimique (ABEL et al., 2010; YAO, 2011). En effet, l’eutrophisation, se traduisant par une prolifération anarchique de végétaux aquatiques de tous genres, est responsable des dégradations abiotiques et biotiques des eaux de surface (CABRITA et al., 2015; PINEDO et al., 2015; PIZARRO et al., 2016; SUTELA et al., 2016). Ainsi, le phosphore a toujours suscité d’importants intérêts d’étude dans les écosystèmes aquatiques.

La dynamique du phosphore dans les eaux de surface, diverse et typique à chacune d'elles, illustre la complexité de son cycle biogéochimique. Si pour les eaux de surface à petits bassins versants (lac, réservoir, étang, etc.), une approche du cycle biogéochimique de ce nutriment est relativement satisfaisante (MELLANDER et al., 2016; SUNOHARA et al., 2016; WANG et LIANG, 2016; YAO et al., 2016a), ce n’est pas le cas pour celles à grands bassins versants (fleuves, lagunes, océans, etc.). Pour ces entités, il est fait recours à la modélisation tant pour apprécier les facteurs (exogènes et endogènes) intervenant dans son cycle biogéochimique que pour extrapoler son évolution en leur sein et sur leur bassin versant. La modélisation du phosphore dans les eaux de surface connait un essor remarquable depuis 1990 eu égard à la croissance vertigineuse des modèles consacrés au phosphore. L’étude réalisée par ROBSON (2014) a montré que la quasi-totalité des modèles consacrés à ce sujet sont des modèles de connaissances. Ainsi, les modèles de type « boite noire » semblent -ils être lésés en dépit de leur performance reconnue dans tous les domaines. Parmi ceux-ci figurent les réseaux de neurones artificiels (RNA). Ce véritable outil statistique connait depuis toujours un grand succès dans la modélisation des phénomènes et des procédés. Cette situation s’explique par sa parcimonie et sa rapidité qui permet de les généraliser (MANDAL et al., 2015; XU et al., 2015). Plusieurs variantes de RNA existent, dont le plus connu est le perceptron multicouche (PMC). La capacité de ce type de RNA à modéliser les problèmes aquatiques n’est plus à démontrer, particulièrement l’eutrophisation (CHANG et al., 2015; HUANG et GAO, 2017; HUO et al., 2013; MA et al., 2014; MULLER et MULLER, 2015; SHOULIANG et al., 2013). Le PMC se caractérise par sa typologie et son fonctionnement. En effet, il possède une seule couche d’entrée, au moins une couche cachée et une couche de sortie. Il est généralement utilisé avec une seule couche cachée du fait que certains travaux ont montré que dans cette configuration il permet d’approximer n’importe quelles fonctions non linéaires et complexes (ZHANG, 2003). Chaque neurone artificiel est un mini processeur qui calcule la somme des données reçues à son entrée et fournit le résultat de calcul à sa sortie. Il n’y a pas de connexions entre les neurones artificiels d’une même couche. Chaque connexion est pondérée par un « poids ». Il n’est pas défini de fonction sur la couche d’entrée. Cependant, sur la(les) couche(s) cachée(s) il est défini une fonction d’activation, et sur la couche de sortie, la fonction simple de linéarité. Le réseau est synchronisé et non rétroactif (AICHOURI et al., 2015).

À l’instar de tout le système Ébrié, la baie de Tiagba est sujette à de fortes pressions anthropiques. Cette situation entraine sa dégradation, traduite par son état d’hypereutrophisation (YAO, 2011). Une autre illustration est apportée par le taux de croissance du phosphore (+0,144 pour le phosphore total et +0,636 pour le phosphore minéral) dans cette baie lagunaire sur ce dernier quart de siècle, noté en comparant ses teneurs moyennes obtenues par CARMOUZE et CAUMETTE (1985) sur la période de 1976 à 1979 à celles de YAO (2011) sur la période de 2006 à 2009. À cet effet, il importe de mener des actions visant sa réhabilitation et sa protection dans le cadre de son développement durable. Ce fait passe d’abord par la connaissance d’un certain nombre de processus lié à sa pollution. C’est dans cette optique que l’évolution spatiotemporelle du phosphore minéral dans les eaux de cette baie lagunaire a été modélisée par le PMC.

2. Matériel et méthodes

2.1 Présentation de la zone d’étude

La baie lagunaire de Tiagba est localisée précisément entre 4°40' et 4°45' de longitude ouest à la latitude nord de 5°20' et à 73 m au-dessus du niveau de la mer. Ses différentes caractéristiques morphologiques et hydrologiques sont données à la figure 1. Située à 80 km du canal de Vridi (unique entrée des eaux marines dans le système Ébrié), cette baie est soumise à une influence amoindrie de l’océan Atlantique. Son taux de renouvellement, faible (0,24 par an), est essentiellement dû aux apports météorites. Ses apports, relativement faibles, sont du fait de la rivière Ira par le biais de la baie de Cosrou via la passe de « Cosrou » et du fleuve Bandama par le truchement du canal d’Assagny et de la passe d’« eaux libres du chenal central » d’une part, et des eaux météorites de ruissellement du bassin versant d’autre part.

Figure 1

Caractéristiques morphologiques et hydrologiques de la baie lagunaire de Tiagba

Morphologic and hydrologic characteristic of Tiagba Lagoon Bay

Caractéristiques morphologiques et hydrologiques de la baie lagunaire de Tiagba

-> See the list of figures

2.2 Choix des paramètres pertinents

En se référant aux travaux de YAO (2011), les paramètres interagissant avec la dynamique du phosphore dans les eaux de la baie de Tiagba sont à priori : la température, le pH, le potentiel d’oxydoréduction, la transparence, les matières en suspension (MES), l’oxygène dissous, la chlorophylle a, la pluviométrie dans la zone d’étude, le débit du fleuve Bandama et le débit de la rivière Ira. Le choix définitif des paramètres jugés pertinents dans la dynamique du phosphore minéral dans cette baie lagunaire a été fait à partir de l’analyse en composantes principales (ACP). L’ACP a été appliquée sur une base de 6 610 données composées de 661 échantillons (observations). Dans cette étude, l’ACP a été réalisée à partir du logiciel Statistica version 7.1.

2.3 Développement du PMC dans cette étude

Le développement du PMC dans cette étude a été réalisé à partir du logiciel Matlab R2015a conjointement avec le module Statistics and Machine Learning Toolbox.

2.3.1 Scénarios étudiés

Deux scénarios ont été abordés dans le cadre de cette étude :

  • Scénario 1 : modélisation statique du phosphore minéral. Le seul paramètre de sortie est la teneur en phosphore minéral (Y1), tandis que les teneurs des paramètres jugés pertinents constituent les paramètres d’entrée (Xi);

  • Scénario 2 : modélisation dynamique du phosphore minéral. Deux paramètres de sortie sont utilisés dans ce cas, à savoir les teneurs en phosphore minéral aux temps t (mois en cours Y[t]) et à la date t + 1 (mois suivant Y[t + 1]). Aux teneurs des paramètres pertinents, il est ajouté le paramètre temps (mois) pour constituer les paramètres d'entrée (Xi).

Au cours de cette étude, les teneurs des différents paramètres utilisées sont celles fournies par YAO (2011) sur la période 2007-2009. Le paramètre temps (mois) a été codé entre 0 et 22.

2.3.2 Conditions du déroulement du PMC

D’une manière générale, les bases de données doivent subir un prétraitement afin d’être adaptées aux entrées et sorties des modèles mathématiques stochastiques, tel que le PMC. Un prétraitement courant consiste à effectuer une normalisation appropriée qui tient compte de l’amplitude des valeurs acceptées par les modèles (BASHEER et HAJMEER, 2000; MANSSOURI et al., 2015). Cette base de données est constituée de différentes variations des variables indépendantes (entrées du modèle) et dépendantes (sortie du modèle). Dans cette étude, les différents paramètres ont été normalisés suivant l’équation 1 et codés dans un intervalle compris entre 0 et n (n appartenant aux entiers naturels) par le logiciel Matlab R2015a conjointement avec le module Statistics and Machine Learning Toolbox.

où xni est la donnée normalisée, comprise entre -1 et +1, xi est la donnée à sa valeur initiale, xmax est la valeur maximale de l’ensemble de données et xmin est la valeur minimale de l’ensemble de données.

Pour l’obtention de faibles erreurs de prédiction, les poids du réseau sont initialisés avant leur modification au cours du processus d’apprentissage. L’architecture du réseau a été optimisée en faisant varier le nombre de couches cachées de 1 à 15 en tenant compte des coefficients de corrélation (R) et de la moyenne carré des erreurs (MCE ). Pour chaque valeur de la couche cachée, les simulations ont été effectuées 1 500 fois et le meilleur résultat de l’architecture du réseau correspondant a été enregistré. Ce meilleur résultat correspond à celui présentant simultanément les plus fortes valeurs de R lors des phases d’apprentissage (Rapp) et de validation (Rval), mais aussi les plus faibles valeurs de MCE dans ces deux phases. Durant toutes les simulations, l’algorithme de Levenberg-Marquardt (LEVENBERG, 1944; MARQUARDT, 1963) a été utilisé pour accélérer la phase d’apprentissage. Le taux d’apprentissage est fixé au départ à 0,2 et progressivement réduit à 0,01 à des pas de 0,05. À cet effet, 50 % et 25 % de la base de données ont été respectivement utilisés pour l’exécution des phases d’apprentissage et de validation. La fonction de transfert utilisée entre la couche d’entrée et la couche de sortie est la tangente hyperbolique (Tanh). Ainsi, chaque neurone caché produit-il une sortie Yi selon l’équation 2 :

où wi représente les poids, xi les entrées et ßi le biais associé à la sortie Yi.

La fonction linéaire simple (y = x) est utilisée comme fonction de transfert entre la couche cachée et la couche de sortie. De ce fait, chaque neurone de sortie produit une sortie Yj suivant l’équation 3 :

où wj représente les poids, yi les neurones cachés et ßj le biais associé à la sortie Yj.

2.2.2 Choix du modèle et conditions de sa validation finale

2.2.2.1 Choix du modèle

Le meilleur modèle traduisant au mieux le phénomène étudié correspond à celui présentant simultanément les valeurs les plus élevées de Rapp et de Rval d’une part, et la plus faible valeur de la MCE lors de la phase de validation (MCEval) d’autre part. Cependant, si les valeurs les plus élevées de Rapp et Rval, et la plus faible valeur de MCEval sont distinctement obtenues pour des modèles différents, le meilleur compromis est celui qui présente la plus grande valeur de R (Équation 4), mais aussi une MCEval parmi les plus faibles pour les modèles ayant une sortie. Pour ceux ayant deux sorties, le meilleur modèle est celui présentant la plus grande valeur de R' (Équation 5) et ayant une MCEval parmi les plus faibles (YAO et al., 2016a). R et R' sont donnés par :

où R est la moyenne arithmétique de Rapp et Rval et R' est la moyenne arithmétique de R pour deux sorties du PMC.

2.2.2.2 Validation finale du modèle

La validation finale du modèle consiste à juger sa capacité de prédiction de la dynamique du phosphore dans la baie lagunaire de Tiagba. Cela en utilisant les poids et les biais calculés durant l’apprentissage pour les appliquer à une autre base de données. Cette phase du PMC s’appelle le « test ». Vingt-cinq pourcent (25 %) de la base de données, normés suivant l’équation 1, ont été utilisés à cet effet.

Le modèle choisi est validé finalement si les conditions suivantes sont simultanément satisfaites :

  • R2val > 0,5 (YAO, 2011; YAO et al., 2016a), en d’autres termes si le modèle traduit à plus de 50 % le phénomène étudié lors de la phase de validation;

  • la MCE et la racine des moyennes des carrés des erreurs (RMCE ) lors de la phase de test doivent être relativement très faibles;

  • l’erreur moyenne de prévision (emoy) entre les valeurs de phosphore minéral obtenues expérimentalement (Yobs) et celles prédites (Ypr) par le modèle lors du test, doit être relativement très faible. Cette erreur est calculée suivant l’équation 6 :

où N est le nombre d’échantillons dans la base de données du « test ».

  • l’erreur moyenne relative de déviation (Δ [%]) entre les valeurs de phosphore minéral obtenues expérimentalement (Yobs) et celles prédites par le modèle (Ypr) lors du test doit être inférieur à 10 % tel recommandé pour les modèles statistiques (NOUMI, 2004; YAO, 2011). Elle s’obtient selon l’équation 7 :

où N est le nombre d’échantillons dans la base de données du « test ».

3. Résultats et discussion

3.1 Résultats

3.1.1 Choix des paramètres pertinents

Dans cette étude, cinq paramètres ont été jugés pertinents dans la dynamique du phosphore à l’issue de l’application de l’ACP aux dix paramètres préalablement choisis à la section 2.2. Il s’agit de la transparence, des MES, de la chlorophylle a, de la pluviométrie dans la zone d’étude et du débit du Bandama.

Le tableau 1 présente les valeurs propres et les statistiques associées de l’ACP obtenu à partir de ces cinq paramètres et du phosphore minéral. Les deux premiers facteurs à eux seuls représentent 56,22 % de la variance totale, dont 34,14 % pour F1 et 17,38 % pour F2. Le facteur F1 est très important par rapport aux autres. Quant au tableau 2, relatif à la matrice de corrélation de Bravais-Pearson, il montre une très forte corrélation entre le phosphore minéral et la transparence (r = 1,00). Cette corrélation est très significative et témoigne de l’affinité entre ces deux éléments. Par contre, les corrélations du phosphore minéral avec les MES (r = 0,14) et la chlorophylle a (r = 0,08) sont très faibles. Il en est de même pour le débit du Bandama avec les MES (r = -0,11) et la pluviométrie (r = 0,13), de la chlorophylle a avec les MES (r = 0,10) et le débit du Bandama (r = 0,29), des MES avec la transparence (r = 0,13).

Tableau 1

Valeurs propres et statistiques associées de l’analyse en composantes principales (ACP) des six variables

Eigenvalues and related statistics from Principal Component Analysis (CPA) of the six variables

Valeurs propres et statistiques associées de l’analyse en composantes principales (ACP) des six variables

-> See the list of tables

Tableau 2

Matrice de corrélation de Bravais-Pearson pour les six paramètres. Corrélations significatives marquées à p < 0,05, n = 661 (observations à VM ignorées)

Bravais-Pearson correlation matrix for the six parameters. Significant correlations at p < 0,05, n = 661 (MV observations not taken into account)

Matrice de corrélation de Bravais-Pearson pour les six paramètres. Corrélations significatives marquées à p < 0,05, n = 661 (observations à VM ignorées)

a Matières en suspension

-> See the list of tables

La projection de ces paramètres dans le plan factoriel F1-F2, met en évidence deux regroupements des paramètres étudiés dans les échantillons d’eau (Figure 2) :

  • G1, contenant le phosphore minéral, la transparence et les MES;

  • G2, regroupant la chlorophylle a, la pluviométrie dans la zone d’étude et le débit mensuel du Bandama.

Figure 2

Projection des six paramètres dans le plan factoriel F1-F2

Projection of the six parameters in the factorial plan F1-F2

Projection des six paramètres dans le plan factoriel F1-F2

-> See the list of figures

G1 traduit partiellement les processus intervenant dans la minéralisation de la matière organique, tandis que G2 exprime partiellement les facteurs influençant les activités photosynthétiques. Ces deux entités sont complémentaires. Cependant, leur affinité dans ce cas d’étude tend à être masquée par l’état hypereutrophe de la baie lagunaire de Tiagba. Ainsi, le facteur F1 semble-t-il rendre compte des conditions d’acquisition du chimisme du phosphore minéral. Ce facteur est déterminé par le phosphore minéral et la transparence. En effet, la luminosité est d’une grande importance dans la dégradation et la minéralisation de la matière organique (COBLE et al., 2015; FOTIOU et al., 2015; SONG et al., 2016), donc à la production du phosphore minéral.

Ces paramètres permettent de former des bases de 3 966 données pour la modélisation statique et de 4 627 données pour la modélisation dynamique de ce nutriment (YAO et al., 2016b).

3.1.2 Choix des meilleurs modèles

Les résultats obtenus lors des simulations pour les deux scénarios étudiés sont résumés dans les tableaux 3 et 4. À l’analyse de ces résultats, l’on note que les valeurs les plus élevées de Rapp et Rval, de même que la valeur la plus faible de MCEval, sont obtenues pour des modèles distincts. Ainsi, les modèles 5-14-1 et 6-14-2 représentent-ils les meilleurs respectivement pour les scénarios 1 et 2. Les représentations architecturales de ces deux modèles sont données par la figure 3.

Tableau 3

Caractéristiques des différents modèles établis pour le scénario 1

Characteristics of different models for scenario 1

Caractéristiques des différents modèles établis pour le scénario 1

-> See the list of tables

Tableau 4

Caractéristiques des différents modèles établis pour le scénario 2

Characteristics of different models for scenario 2

Caractéristiques des différents modèles établis pour le scénario 2

a Moyenne arithmétique de Rapp (t) et Rval (t)

b Moyenne arithmétique de Rapp (t + 1) et Rval (t + 1)

c Moyenne arithmétique de R1 et R2

-> See the list of tables

Figure 3

Architecture des modèles a) 5-14-1 et b) 6-14-2

Architecture of models a) 5-14-1 and b) 6-14-2

Architecture des modèles a) 5-14-1 et b) 6-14-2

-> See the list of figures

3.1.3 Validation finale des modèles

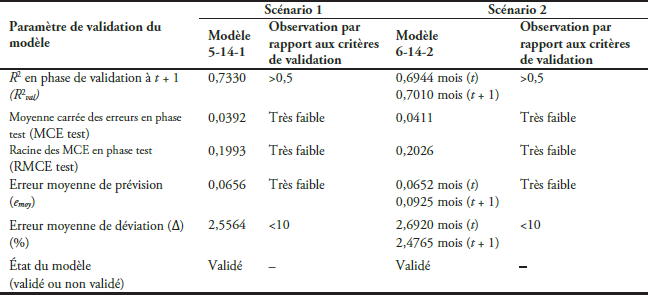
En se référant au tableau 5, les modèles 5-14-1 et 6-14-2 respectent tous les critères de validation de modèles énoncés dans la section 2.2.2.2. Ainsi, sont-ils tous deux validés.

Tableau 5

Validation finale des modèles 5-14-1 et 6-14-2

Final validation of models 5-14-1 and 6-14-2

Validation finale des modèles 5-14-1 et 6-14-2

-> See the list of tables

Pour le scénario 1, le modèle 5-14-1 explique à 93,12 % les variations spatiotemporelles des cinq paramètres d’entrée mise en jeu et prédit à 73,30 % l’évolution statique du phosphore minéral dans la baie lagunaire de Tiagba. Quant au modèle 6-14-2 destiné au scénario 2, il explique à 93,10 % et 91,71 % la variation spatiotemporelle des six paramètres d’entrée mise en jeu respectivement pour le mois (t) et le mois suivant (t + 1). Il prédit à 69,44 % et 70,10 % la dynamique du phosphore minéral au mois (t) et au mois (t + 1) respectivement. Le coefficient de corrélation entre les valeurs expérimentales et celles calculées par le modèle est de 0,80545 pour le modèle 5-14-1 et 0,85761 pour 6-14-2 (Figure 4).

Figure 4

Représentation des valeurs expérimentales normalisées en fonction des valeurs calculées normalisées pour les modèles : a) 5-14-1 et b) 6-14-2

Representation of normalized experimental values as function of normalized predicted values for models: a) 5-14-1 and b) 6-14-2

Représentation des valeurs expérimentales normalisées en fonction des valeurs calculées normalisées pour les modèles : a) 5-14-1 et b) 6-14-2

-> See the list of figures

3.2 Discussion

Les modèles 5-14-1 et 6-14-2 permettent de prédire respectivement les évolutions statique et dynamique du phosphore dans les eaux de la baie lagunaire de Tiagba avec des marges d’erreurs comprises entre 26,67 % et 30 %. Ces marges d’erreurs pourraient s’expliquer par la sous-estimation de certains processus liés au cycle biogéochimique du phosphore dans cette étude tel que le flux de transfert du phosphore dans les systèmes sol-sédiment et sédiment-eau, les activités benthiques, la mobilité du phosphore dans les sédiments, etc.

Ces résultats sont jugés relativement satisfaisants dans la mesure où ils permettent de confirmer la grande influence des apports météorites (environ 70 %) sur la dynamique du phosphore minéral dans les eaux de cette baie lagunaire, déjà soupçonné par YAO (2011). Ainsi, ces différents modèles établis peuvent-ils servir dans le cadre d’une prise de décisions visant à la réhabilitation, la protection et la gestion à court et long terme de cette baie lagunaire. L’une des techniques susceptibles d’être proposée dans ce cadre est d’y favoriser l’apport du fleuve Bandama en élargissant et draguant régulièrement le canal d’Assagny. En effet, YAO (2011) a noté que cet apport fluviatile inhiberait la croissance de ce nutriment, en même temps que celle du phytoplancton. Aussi, faudra-t-il limiter voire interdire l’utilisation des fertilisants phosphorés sur le bassin versant de cette baie lagunaire, où la pratique agricole est intense.

Par ailleurs, l’utilisation des RNA dans cette étude est d’une originalité dans la mesure où la quasi-majorité des modèles consacrés à la modélisation du cycle biogéochimique du phosphore dans les eaux de surface sont des modèles de connaissances (ROBSON, 2014). Également, contrairement à ceux-ci (GROWA/MEPhos [GUSE et al., 2007; TETZLAFF, 2006], MONERIS [BEHRENDT et al., 2000], CASA model [WANG et al., 2010], SWAT model [FONTAINE et al., 2002; FREIHOEFER et McGINLEY, 2009; SANTHI et al., 2001], WEE et WEEE [DUCHESNE et al., 2016], etc.) qui ont un champ d’action réduit aux plans d’eau pour lesquels ils ont été établis, les RNA sont dans leur quintessence applicables pour la modélisation des processus aquatiques de tous genres dans n’importe quel plan d’eau. Ainsi, sont-ils de véritables outils importants pour la gestion des bassins des eaux de surfaces.

4. Conclusion

Cette étude vient encore une fois démontrer la capacité des RNA à modéliser les phénomènes aussi complexes que les processus biogéochimiques tel que celui du phosphore minéral. Les deux modèles établis, jugés satisfaisants, peuvent être utilisés en complémentarité avec ceux de YAO et al. (2016a) dans le cadre de la lutte contre l’eutrophisation d’une part, et servir à la gestion de ce plan d’eau dans le cadre général de son développement durable d'autre part.