Existe-t-il une relation entre les modèles pluie-débit au pas de temps pluriannuel ?

Mouelhi, Safouane

doi:https://doi.org/10.7202/1006455ar

1. Introduction

Généralement il existe deux formes de modèles pluie-débit au pas de temps pluriannuel : soit une cartographie ou soit une écriture mathématique utilisant des fonctions usuelles. Chacune de ces formes adopte une approche modélisatrice appropriée :

L’approche d’experts (Domokos et Sass, 1990; Tryselius, 1971) se présente comme une cartographie de quelques régions ciblées. La carte obtenue reste la vision personnelle d’un expert. Son degré de confiance repose essentiellement sur le savoir encyclopédique et le bon sens hydrologique de l’auteur.

L’approche empirique consiste à relier les caractéristiques extraites des chroniques de débits aux caractéristiques géomorphologiques, hydrologiques et climatologiques des bassins versants (Bishop et Church, 1992; Cemagref, 1986; Dingman, 1981; Liebscher, 1972). Les modèles issus de cette approche sont présentés soit sous forme cartographique, soit sous forme mathématique.

L’approche géostatistique est une interpolation de champs stochastiques, chaque champ étant une réalisation d’un phénomène aléatoire (Sauquet, 2000).

Quant à l’approche par bilan, les éléments de celui-ci se décomposent en flux d’entrée (les précipitations liquides et solides) et en flux de sortie (infiltration profonde; évaporation du sol; transpiration des végétaux; débits). L’évapotranspiration potentielle (E) est une borne supérieure de l’évapotranspiration réelle (ETR) qui intervient directement dans le bilan en eau. Les modèles issus de cette approche prennent une forme mathématique simple adaptable à chaque bassin versant. Ces modèles font l’objet de cet article.

Dans la littérature portant sur l’hydrologie, de nombreux modèles pluie-débit au pas de temps pluriannuel sont proposés. Pour une meilleure compréhension et utilisation de ces modèles, il parait intéressant de les répertorier, détecter les éventuelles relations entre ceux-ci et voir comment on peut améliorer leurs performances. Le présent article tente de répondre à ces questions. La première partie est consacrée à l’explication de la méthode de modélisation suivie et à la présentation de l’échantillon de données. La seconde partie présente l’application des modèles retenus sur cet échantillon de données ainsi que la méthode ayant servi à la visualisation de la relation entre ceux-ci. Enfin, une méthode d’amélioration aboutissant à de nouvelles formes des modèles est proposée.

2. Méthode de modélisation

La modélisation pluie-débit au pas de temps pluriannuel a été effectuée dans un cadre global de construction des modèles GR(s) au Cemagref (Établissement français public à caractère scientifique), initié par C. Michel (Initiateur des modèles GR(s)). Par souci de cohérence, la même méthode retenue et validée au cours des travaux de modélisation aux pas de temps journalier (Perrin, 2000; Perrinet al., 2001, 2003), mensuel et annuel (Mouelhi, 2003; Mouelhiet al., 2006a, b) a été adoptée.

2.1. Échantillon de données

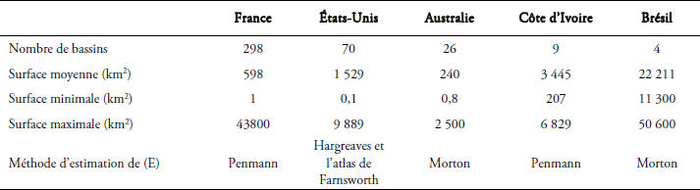
L’échantillon de données se compose de 407 bassins versants (Tableau 1) ayant déjà servi, en totalité ou en partie, tout au long du développement des modèles pluie-débit ‘GR(s)’ (LeMoine, 2008; Mathevet, 2005; Mouelhi, 2003; Mouelhiet al., 2006a, b; Oudin, 2004; Oudinet al., 2008; Oudinet al., 2006; Perrin, 2000; Perrin et al., 2001, 2003; Tangara, 2005).

Tableau 1

**Quelques caractéristiques de l’échantillon de données.**

**Table 1. Sample characteristics data.**

Brièvement, cet échantillon rassemble des bassins de différentes origines et représente des conditions climatologiques, hydrologiques et anthropiques assez variées. Nous avons, d’une part, des conditions semi-arides en Australie ou au sud des États–Unis, avec des cours d’eau connaissant des débits seulement quelques jours dans l’année, et, d’autre part, des conditions tropicales humides dans le sud de la Côte d’Ivoire ou le nord de l’Australie. La taille des bassins versants varie sur une large gamme, de 0,1 à plus de 50 000 km². Cet échantillon reflète aussi une grande variété de comportements saisonniers. En effet, il existe des bassins avec des saisons pluvieuses et sèches très contrastées, et aussi des régimes assez uniformes tout au long de l’année tant au niveau de la pluie que du débit.

Les données de pluie (P), de débit (Q) ainsi qu’une partie des données d’évapotranspiration potentielle (E) sont fournies au pas de temps journalier. Il a fallu agréger ces données au pas de temps pluriannuel pour répondre aux objectifs de ce travail.

Les modèles utilisés pour l’estimation de la variable (E) sont : Penman pour les bassins français et ivoiriens (Penman, 1948), Hargreaves et l’atlas de Farnsworth pour les bassins américains (Farnsworthet al., 1982; Hargreaves et Samani, 1982), Morton (Morton, 1983) pour les bassins australiens et brésiliens. Oudin (2006) a testé l’impact de la variabilité des méthodes d’estimation de (E) sur la performance des modèles conceptuels globaux. La sensibilité des modèles pluie-débit au pas de temps pluriannuel à l’évapotranspiration potentielle n’est pas traitée dans cet article.

2.2. Variable cible, fonction critère, méthode d’optimisation

La variable cible retenue est la racine de débit () plutôt que le débit (Q). Ce choix a été discuté et approuvé par les travaux de Perrin (2000) et repris dans les travaux de Mouelhi (2003), Oudin (2004) et Mathevet (2005). Au pas de temps pluriannuel, ce choix nous permet aussi de ne pas favoriser les bassins humides aux bassins arides lors du processus d’optimisation.

La fonction critère retenue est celle dite critère de Nash, noté ici (F) (Nash et Sutcliffe, 1970). En effectuant la transformation choisie (racine de Q), ce critère s’écrit :

avec N : le nombre total de valeurs calculées et observées (407 bassins versants); Q : lame d’eau écoulée observée (mm•an-¹); : lame d’eau écoulée estimée par le modèle (mm•an-¹); : moyenne sur N valeurs de la racine carrée des lames d’eau écoulées observées.

(F) prendra des valeurs allant de -∞ jusqu’à 1 (F ε ]-∞,1]). Le modèle est considéré comme performant quand les débits estimés se rapprochent des débits observés, c’est-à-dire, quand (F) est proche de 1.

La méthode d’optimisation retenue est celle dite « pas à pas » (Michelet al., 1989; Nascimento, 1995). C’est une méthode locale directe qui opère une optimisation (maximisation ou minimisation) d’une fonction objective choisie par l’utilisateur (indépendamment de la méthode). Il s’agit ici d'une maximisation de la fonction (F) (Équation(1)). Cette méthode adopte une stratégie de déplacement, le long des axes de l’espace des paramètres, avec un pas de recherche pouvant varier d’une itération à l’autre. Elle a prouvé une meilleure performance par rapport à d’autres méthodes dans le contexte de la modélisation pluie-débit conceptuelle globale (Perrin, 2000).

L’évaluation de la robustesse des modèles a requis l’utilisation de la technique dite « du double échantillon » ou split-sample test » (Klemes, 1986). Il s’agit de découper la période d’observation en deux sous-périodes, l’une pour le calage et l’autre pour le contrôle (ou validation). Leurs rôles seront permutés de telle sorte que nous ayons deux périodes de calage et deux périodes de contrôle. Ainsi le modèle testé ne sera évalué qu’au contrôle. Toutefois, au pas de temps pluriannuel et pour chaque bassin versant, nous ne disposons pas de séries chronologiques. Chaque bassin est plutôt représenté par un triplet de moyennes interannuelles de (P, E et Q).

Pour adapter cette technique au pas de temps pluriannuel, l’échantillon de 407 bassins a été découpé de la façon suivante : Un premier sous-échantillon regroupant les bassins de rang (2n) et un deuxième sous-échantillon regroupant les bassins de rang (2n+1) où n varie de 0 à 203. Le fichier de données est organisé d’une façon décroissante par rapport au nombre de bassins de chaque pays. Il est composé alors d’une première partie représentant les bassins versants de la moitié nord de la France, d’une deuxième partie relative à la moitié sud de la France et d’une troisième partie relative aux bassins américains, australiens, ivoiriens et brésiliens. Ainsi, les deux sous-échantillons obtenus lors du découpage gardent une variabilité hydro-climatologique assez importante, mais similaires.

Les valeurs de (F), en gardant la même forme de l’équation (1), seront donc calculées de la façon suivante : le calage sur le premier sous-échantillon fournit un vecteur paramètres A₁. En utilisant le modèle avec le vecteur paramètre A₁ sur le deuxième sous-échantillon, on peut calculer les débits , (i) variant de 0 à 203. Ensuite, on cale le modèle sur le deuxième sous-échantillon, ce qui donne un vecteur paramètres A₂. L’utilisation du modèle, avec le vecteur paramètres A₂, donne sur le premier sous-échantillon les débits , (i) variant de 1 à 203. Le critère de Nash, issu des deux façons de calcul des débits en contrôle, est alors la valeur de Fmg (F moyen global) :

Dans le cas d’un modèle sans paramètre, le critère donnera la même valeur que l’équation (1), c’est-à-dire (Fmg) égale à (F). De cette façon, l’apport de l’affectation de paramètres dans un modèle peut être évalué.

Ces formes de critère de Nash (F et Fmg) utilisent comme modèle de référence la racine d’un débit constant égal au débit moyen pluriannuel de l’ensemble de l’échantillon de 407 bassins versants (). Ce dernier semble être un modèle de référence trop exigeant dans le cas des bassins semi-arides ou à faible rendement. Ce type de bassins peut influencer alors sensiblement la valeur de (Fmg), donc le jugement de la robustesse du modèle mis à l’épreuve sur l’ensemble des 407 bassins. Un critère de bilan par rapport à la totalité de l’échantillon de données () donnerait de meilleures valeurs mais l’effet de chaque bassin sur l’ensemble de l’échantillon de données ne sera pas pris en compte et les résultats seront ainsi biaisés. C’est pour cela que le choix du critère a été plutôt porté sur la forme donnée par (Fmg) de l’équation (2), bien qu’il soit plus exigeant par rapport à d’autres critères.

3. Choix de modèles et adimensionnelle

Au pas de temps pluriannuel, les modèles sont présentés comme une relation reliant les variables (Q), (P) et (E) [Q = f(P,E)]. La dimension de ces variables est le millimètre par an (mm•an-¹). Une écriture adimensionnelle permet de ramener la relation à une fonction d’une seule variable. Ainsi, il sera plus facile de comparer les modèles et de visualiser leurs limites physiques. Pour ce faire, le théorème de Vaschy-Buckingham, appelé aussi théorème des Pis a été appliqué. Ainsi, la forme des modèles retenus a été transformée selon la relation « Q/P = f(P/E) » où « y = f(x) » avec (y = Q/P et x = P/E). Dans ce qui suit sont présentés les modèles choisis ainsi que leur transformation adimensionnelle. Seuls les plus basiques et les plus répandus ont été retenus.

3.1 Modèle de Schreiber (1904)

Schreiber a proposé un modèle qui permet de calculer l’évapotranspiration réelle (ETR) à partir de la pluviométrie (P) et de l’évapotranspiration potentielle (E) au pas de temps interannuel en utilisant la fonction exponentielle (Schreiber, 1904). L’introduction de cette formule dans l’équation du bilan hydrologique (Q = P – ETR) se traduit comme suit :

L’écriture adimensionnelle du modèle Schreiber prend la forme de :

À titre indicatif, cette forme a été retrouvée dans le modèle proposé par Vandewiele (1991).

3.2 Modèle d’Ol’dekop (1911)

Le modèle proposé en 1911 par Ol’dekop est un modèle sans paramètres. Il utilise une des fonctions mathématiques usuelles, la fonction « tangente hyperbolique » (Bhaskar, 1999). Il s’écrit sous la forme suivante :

L’écriture adimensionnelle prend la forme de :

Une variante de ce modèle a été utilisée afin de détecter un changement de l’écoulement annuel de bassins australiens suite à l’action anthropique (Chiew et Mahon, 1993).

3.3 Modèle de Turc (1954)

Turc avait adopté comme point de départ l’équation du bilan hydrologique (Turc, 1954). Si les moyennes sont calculées pour une période suffisamment longue (pas de temps pluriannuel), la variation de la rétention de l’eau dans le bassin est en général négligeable par rapport aux autres termes du bilan. Par la suite, la quantité d’eau apportée par les précipitations (P) est égale à celle qui s’est écoulée à l’exutoire du bassin (Q) augmentée de celle qui s’est évaporée (ETR), ce qui s’écrit :

Turc a rassemblé un échantillon de 254 bassins de caractéristiques hydro-climatiques assez variables. Ces bassins, pour lesquels les valeurs de (P) de (Q) et de la température (t) sont relativement bien connues, appartiennent à différentes parties du globe : Europe, Afrique, Amérique et Java. En essayant de relier ces valeurs, Turc a établi la formule suivante :

avec t : température (°C) et L(t) = 300 + 25t + 0,05t³.

(L) peut être considérée comme une estimation de l’évapotranspiration potentielle. Dans notre cas, l’évapotranspiration potentielle est déjà acquise, et il est inutile de la recalculer en fonction de la température. En remplaçant donc (L) par (E), l’équation (8) prend la forme :

En introduisant l’équation (9) dans celle du bilan hydrologique, le modèle s’écrit :

En 1964, Pike a proposé une autre version du modèle de Turc en remplaçant la constante 0,9 par 1. Cette forme paraît plus simple et a été plus efficace sur cet échantillon de données par rapport au modèle originel de Turc. Introduire ici ces résultats encombrerait ce document. Toutefois, ces tests ont été bien détaillés dans les travaux de thèse de Mouelhi (2003). La forme du modèle retenu prend alors la forme de :

3.4 Modèle de Tixeront (1963)

L’idée de base de Tixeront se traduisait comme suit : pour de longues périodes d’observations (une trentaine d’années par exemple), il existe une certaine corrélation entre la pluviosité moyenne annuelle et le ruissellement moyen annuel (Tixeront, 1964). Il estimait que ces corrélations existent quand on a affaire à des bassins aux sols « normalement » constitués, ni trop perméables (terrains karstiques ou dunaires), ni trop squelettiques (zones trop arides en particulier). Par la suite, il cherchait une relation simple permettant, pour des bassins « normaux », d’estimer l’écoulement annuel moyen à partir des données pluviométriques et de l’évapotranspiration potentielle. Cette relation s’écrit sous la forme suivante :

Le paramètre (θ) a été trouvé égal à 3 en Afrique du Nord et dans certains pays méditerranéens et du Proche Orient. Il a été trouvé compris entre 4 et 5 dans un bassin du Tanganyka, sous régime de saison pluvieuse chaude. Dans cet article, la valeur du paramètre (θ) est obtenue empiriquement par calage sur l’ensemble de 407 bassins versants. EIle a été trouvé égale à 2.

3.5 Quelles sont les relations entre ces modèles ?

L’étude mathématique, illustrée par un graphique, des équations relatives aux modèles présentés a permis la détection d’une relation entre eux. Un récapitulatif des caractéristiques mathématiques de ces équations est projeté dans le tableau 2.

Tableau 2

**Étude et analyse adimensionnelle des modèles retenus.**

**Table 2. Retained models adimensional analysis study.**

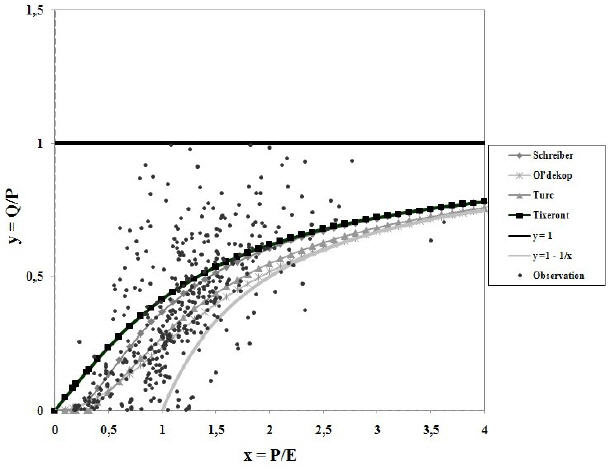
La figure 1 marque bien une certaine similitude entre ces modèles. En effet, ils respectent tous le domaine de définition représenté par (y = 1) et (y = 1 –1/x) soit respectivement (Q = P) et (Q = P – E). Ce qui différencie un modèle de l’autre c’est le comportement à l’origine et à l’infini. Le décollage de l’origine et la convergence vers la bordure inférieure (y = 1 – 1/x) font différencier la forme de ces équations.

Figure 1

**Représentation graphique des modèles dans le plan dimensionnel (x = P/ETP , y = Q/P).**

**Figure 1. Dimensional plane models (x = P / ETP, y= Q/P).**

Le modèle de Turc reste parfaitement collé à l’axe des (x), suivi par le modèle d’Ol’dekop. Ceci se traduit par le fait que Turc considère que le débit est nul pour (P/E < 0,316). Quant au modèle de Tixeront, il décolle d’une façon brutale et reste, par la suite, sensible même pour des bassins à faible pluviométrie ou à forte évapotranspiration potentielle (bassins arides ou semi-arides). Enfin, le modèle de Schreiber représente une fonction qui décolle d’une façon très lente de l’axe des abscisses, grâce à la fonction exponentielle. En ce qui concerne le comportement à l’infini, les modèles qui atteignent le plus lentement la bordure inférieure (y = 1 – 1/x) sont successivement : le modèle Tixeront, puis les modèles de Schreiber et Turc, enfin le modèle d’Ol’dekop qui colle très tôt à cette limite.

Les courbes relatives aux équations des modèles choisis prennent des formes semblables sur le plan (x,y) (où x = P/E et y = Q/P) (Figure 1). Nous proposons ici un modèle supplémentaire dont la courbe correspondante sur le plan (x,y) sera similaire aux autres modèles; il sera désigné par ici par « Modèle Pluriannuel » (MP) :

3.6 Application des modèles retenus sur l’échantillon de données : Résultats et discussion

Les modèles étant sans paramètres, nous n’avons besoin ni d’une méthode de calage, ni de la technique du double échantillon déjà évoquée plus haut. Le seul point qu’on peut retenir de l'approche de modélisation est la variable cible (racine des débits). Il s’agit alors d’appliquer simplement ces équations pour calculer les débits à partir de la pluie et l’évapotranspiration. Le critère de performance est celui de Nash présenté à l’équation (1). Les résultats trouvés sont inscrits au tableau 3.

Tableau 3

**Résultat de l’application des modèles.**

**Table 3. Model’s application results.**

Les valeurs de (F) obtenues sont assez comparables à l’exception de celles relatives au modèle d’Oldékop. Elles varient d’un minimum de 0,535 à un maximum de 0,654, soit un intervalle de 0,119. Ces résultats peuvent être considérés comme assez faibles si on ne prenait pas en compte l’exigence du critère de (F) déjà expliqué plus haut.

La variation de la performance d’un modèle à un autre est expliquée par leur analyse sur le plan dimensionnel. Le modèle d’Ol’dekop semble être le moins performant. Il décolle plus vite par rapport à ceux de Schreiber et Turc. Il a tendance ainsi à surestimer les débits des bassins à faible rendement et vice versa.

En suivant l’ordre croissant des valeurs des (F), on trouve ensuite le modèle de Turc. Ce modèle fixe un seuil en dessous duquel le débit reste nul (). Cependant, il atteint plus vite la bordure (Q = P – E) que le modèle de Schreiber, ce qui peut expliquer son classement par rapport à ce dernier. En se basant seulement sur l’analyse adimensionnelle, le comportement du modèle de Turc aurait pu être modifié en faisant varier l’exposant lié à (x), noté ici (γ) :

où (γ) est appelé l’exposant de Turc. Dans ce qui suit, Turc⁽^γ⁾ fait référence au modèle de Turc généralisé. Le meilleur exposant ainsi trouvé est de l’ordre de 1,5 qui donne une valeur de (F) de 0,647, soit un gain de 4 %. En d’autres termes, cet exposant permet de regagner la limite (Q = P - E ou y = 1 - 1/x) d’une façon moins rapide. Il rejoint ainsi les autres modèles les plus performants.

Comme pour le cas du modèle de Turc, le comportement du modèle de Tixeront aurait pu être changé en modifiant l’exposant (θ) déjà présenté à l’équation (13). Ceci explique la proposition de Tixeront d’avoir différentes valeurs de (θ) en fonction de la typologie des bassins. La meilleure valeur de (θ) trouvée sur l’ensemble des 407 bassins est 2.

4. Tentative d’amélioration : modalités, résultats et discussion

Comme il a été montré plus haut, la modélisation pluie-débit au pas de temps pluriannuel revient à définir une fonction qui respecte le domaine de définition et qui se comporte d’une façon bien déterminée vis-à-vis de ces limites. Comment peut-on améliorer ces modèles?

4.1 Par affectation d’un paramètre

Le but de l’affectation d’un paramètre à un modèle est de laisser un degré de liberté à celui-ci, notamment pour un meilleur ajustement aux données de base. L’introduction d’un paramètre dans les équations relatives aux modèles pluie-débit au pas de temps pluriannuel doit être effectuée de telle sorte que les limites physiques (Figure 1) soient respectées.

Rappelons qu’au pas de temps pluriannuel, un modèle pluie-débit se présente comme une fonction (Q) égale à la pluviométrie (P) à laquelle on soustrait une fonction évaluant l’évapotranspiration réelle [ETR = f(E,P)]. Le paramètre affecté peut être alors soit lié à l’évapotranspiration (E), soit à la pluie (P), soit libre. Pour approuver le choix de l’une ou l’autre solution, différentes possibilités de l’emplacement du paramètre ont été testées sur un modèle « grossier », appelé ici modèle linéaire de référence :

Ce modèle suppose que la totalité de l’évapotranspiration est soustraite de la pluie pour évaluer le débit. Trois choix existent alors pour affecter le paramètre :

1. Affecter un paramètre multiplicatif de l’évapotranspiration E :

2. Affecter un paramètre multiplicatif de la pluie P :

3. Affecter un paramètre de façon qu’il ne dépende ni de la pluie ni de l’évapotranspiration :

Dans le premier et le deuxième cas, le paramètre est alors un coefficient « correctif », sans dimension, de la pluie (P) ou de l’évapotranspiration (E), qui peut varier, mathématiquement, entre zéro et l’infini (ε[0, + ∞[). Dans le troisième cas, le paramètre est une quantité d’eau (mm) qui pourrait représenter une compensation par rapport à l’évapotranspiration. Bien qu’il semble prématuré d’affecter plus d’un seul paramètre dans une formulation mathématique aussi simple que le modèle linéaire, toutes les combinaisons possibles de ces trois cas ont été aussi testées :

Les résultats de l’application de ces modèles « grossiers » pour détecter l’endroit adéquat du paramètre à affecter sont mentionnés au tableau 4.

Tableau 4

**Choix de l’emplacement du paramètre dans un modèle linéaire simple.**

**Table 4. Parameter site choice using a simple linear model.**

Comme déjà signalé, un seul paramètre à caler sur la totalité de l’échantillon semble suffisant. Quant à l’emplacement, en se référant aux valeurs de (Fmg), il semble bien que la meilleure solution est de faire lier le paramètre (a) à l’évapotranspiration potentielle (Q = P-a.E). Il suffira de remplacer l’évapotranspiration potentielle (E) par (aE) pour réécrire les modèles déjà retenus.

4.2 Par affectation de la variable « Indice de Répartition de Pluie »(I_RP)

L’une des limites physiques des modèles est celle relative à (Q = P - E), soit dans le plan adimensionnel y = 1 - 1/x (Figure 1). Cette limite reflète le fait que pour des pluies importantes, la totalité de l’évapotranspiration potentielle peut être soustraite de la pluie pour estimer les débits. Toutefois, la répartition de la pluie selon les saisons devrait jouer un rôle important. Ainsi, le fait de soustraire l’évapotranspiration potentielle de la pluie alors que des périodes humides et froides alternent avec des périodes sèches et chaudes n’est pas justifié. Il semble donc judicieux de tenir compte du régime pluviométrique. Selon la littérature, certains auteurs ont introduit cette information dans les modèles pluie-débit. Liebscher (1972), à titre d’exemple, retient la pluie moyenne (P), la température annuelle moyenne de l’air (TA) et le ratio (PSe/PSh), quotient des précipitations estivales moyennes de mai à octobre inclusivement divisé par les précipitations hivernales moyennes de novembre à avril inclusivement, dans un modèle régressif :

Compte tenu de la disponibilité de données, il a été proposé ici un indice exprimant cette irrégularité de la répartition de la pluie, noté I_RP :

avec P_max : la pluie mensuelle pluriannuelle du mois le plus pluvieux; P_min : La pluie mensuelle pluriannuelle du mois le moins pluvieux; P_m : la pluie mensuelle pluriannuelle moyenne.

La figure 2 permet de découvrir le rôle potentiel de (I_RP) dans l’étalement du nuage de points relatif aux bassins versants. Globalement, une augmentation de la valeur de l’indice de répartition de pluie (I_RP) est accompagnée par un éloignement des observations de la limite (y = 1 – 1/x) ou (Q = P – E). Cette information est prise en compte dans les modalités d’affectation de cet indice dans les modèles retenus.

Figure 2

**Comportement des observations avec IRP sur le plan dimensionnel.**

**Figure 2. Behavior observations using IRP on dimensional plane.**

L’introduction de la variable (I_RP) dans les modèles devrait toujours respecter les limites physiques représentées plus haut. Cette contrainte est à chaque fois vérifiée par un calcul au voisinage des deux frontières. Il a fallu introduire la variable (I_RP) de telle façon que le modèle s’éloigne de la limite (y = 1 – 1/x) ou (Q = P – E) quand l’observation le nécessite. Alors, cette affectation dépend aussi de l’effet de la variation du paramètre (a) sur le comportement du modèle. Rappelons que ce paramètre (a) a tendance à réduire l’évapotranspiration réelle (ETR) et fait éloigner le modèle de la limite (Q = P - E). Par la suite, la variable (I_RP) a alors été liée à ce paramètre pour garder le même effet. Tous les modèles déjà cités ont été repris en faisant intervenir le paramètre (a) et cet indice (I_RP). La réécriture de ces modèles a été effectuée en remplaçant le paramètre (a) par (a/I_RP).

Toutefois, Les données ne sont pas toujours disponibles pour faire introduire cette information. Il a été préférable alors de proposer une forme qui permette de passer d’un cas à l’autre, sans difficulté, en fonction de la disponibilité de données. Le paramètre (a) a été remplacé par a/(I_RP+1) plutôt que par (a/I_RP). Ainsi, dans le cas où on ne tient pas compte de cette variable, il suffira de fixer I_RP à zéro. L’ajout de 1 a aussi permis de contourner les difficultés numériques lors du processus d’optimisation quand I_RP prend des valeurs proches de zéro (a/I_RP tend vers l’infini).

4.3 Résultats et discussions

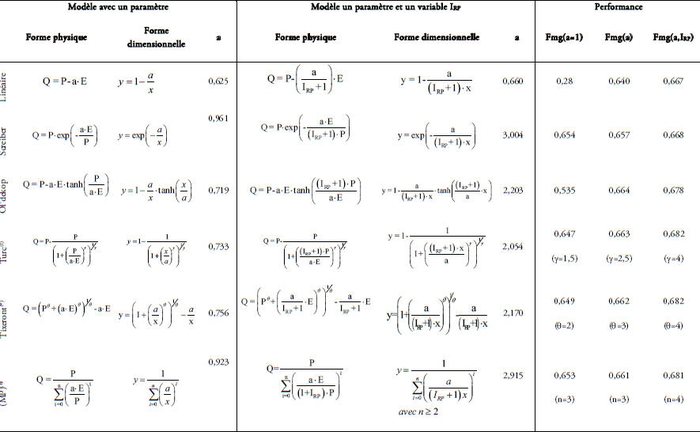
Le tableau 5 rassemble les résultats de l’application des modèles retenus sur l’ensemble de l’échantillon de données. (F) désigne la valeur de « Nash » issue de l’application des modèles avec leurs formes initiales. Fmg(a) illustre les valeurs de « Nash » obtenues suite à l’introduction d’un paramètre (a). Fmg(a,I_RP) présente les valeurs de « Nash » suite à l’introduction à la fois du paramètre (a) et de la variable (I_RP). Pour le cas des modèles en (MP)⁽ⁿ⁾, Turc⁽^γ⁾ et Tixeront⁽^θ⁾, et en suivant une démarche empirique, la valeur correspondant à l’ordre ou l’exposant de ces modèles (n, γ et θ) associée à la meilleure performance, par rapport à l’ensemble de l’échantillon de données (407 bassins), a été détectée.

Tableau 5

**Résultats de l’application des modèles à deux variables explicatives.**

**Table 5. Two explanatory variables model application.**

L’introduction du paramètre (a) et de la variable climatique (I_RP) augmente visiblement la performance des modèles pluriannuels. Le paramètre affecté, sans l’introduction de la variable (I_RP), prend des valeurs inférieures à l’unité, ce qui souligne son caractère correctif de l’évapotranspiration ou simplement le fait que l’ETR reste strictement inférieure à (E) même lorsque (P) tend vers l’infini.

Ce qui paraît relativement « surprenant » c’est que le modèle linéaire, avec sa simplicité extrême et sa formulation évidente, est de performance comparable aux autres modèles. Cependant, sa formulation mathématique peut engendrer des débits souvent nuls, ce qui explique l’utilisation plutôt de fonctions qui donnent des débits positifs.

Le modèle de Schreiber sans paramètre était le plus performant. En affectant le paramètre et la nouvelle variable, il devient pratiquement le moins performant bien qu’un gain ait lieu par rapport à sa forme initiale. Ceci explique la limite mathématique qu’impose une fonction du type exponentielle dans la recherche d’une éventuelle amélioration par rapport à d’autres formulations plus simples du type fonction hyperbolique.

Si l’on se réfère seulement aux valeurs du critère de performance, il sera très difficile de préférer un modèle parmi ceux de Tixeront⁽⁴⁾, Turc⁽⁴⁾, « en (MP)⁽⁴⁾ », Ol’dékop et Schreiber étant donné leurs très proches performances. Toutefois, le paramètre (a) et l’ordre (ou l’exposant) de ces modèles ont été calés empiriquement sur l’ensemble de l’échantillon de 407 bassins. Il serait intéressant, comme l’a fait Tixeront, de régionaliser ces paramètres en fonction de la typologie des bassins versants. Il s’agit d’une perspective intéressante de ce travail.

5. Conclusion

Au pas de temps pluriannuel, chaque bassin versant est représenté par un triplet composé de débit, de pluie et d’évapotranspiration (Q,P,E) et non pas de séries chronologiques. À cette échelle de temps, un modèle pluie-débit prend une forme mathématique liant ces variables (Q), (E) et (P), tous en millimètres par an. Le domaine de définition des équations issues de ces modèles est composé par deux limites : la première se traduit par l’inégalité (P>Q), c’est-à-dire que le débit doit être inférieur à la pluie correspondante. La deuxième se traduit par l’inégalité (Q > P - E) c’est-à-dire qu’à la limite, on ne peut pas retrancher davantage que toute l’évapotranspiration potentielle de la pluie correspondante pour avoir le débit. Ces limites supposent donc que le système « bassin versant » est fermé, avec la pluie comme entrée et le débit et l’évapotranspiration comme sorties.

Le jeu de modèles adopté dans ce travail se traduit par des fonctions mathématiques simples. Ils se présentent globalement dans le plan adimensionnel (x = P/E, y = Q/P) sous forme de courbes semblables, se trouvant généralement au milieu des observations, respectant les limites du domaine de définition. En se référant à cette forme, un modèle supplémentaire a été proposé, désigné par (MP). Rien qu’en changeant le comportement des équations issues des modèles retenus par rapport aux limites physiques, il a été possible d’en améliorer quelques-uns.

Une nouvelle tentative d’amélioration de la performance a été effectuée par affectation de paramètres à caler. Il a fallu alors adapter la technique du double échantillon aux spécificités du pas de temps pluriannuel où un seul paramètre semble bien suffisant. La meilleure façon d’introduire ce paramètre est de le faire lier à l’évapotranspiration (E) comme coefficient multiplicatif. Les valeurs trouvées du paramètre montrent que celui-ci a tendance à réduire l’évapotranspiration réelle.

Finalement, une nouvelle variable (I_RP) appelé « indice de répartition de la pluie » qui prend en compte, comme son nom l’indique, la distribution de la pluie au cours d’une année, a été introduite dans ces modèles. Cette tentative a permis d’améliorer encore tous les modèles tout en notant qu’à cette échelle de temps, l’utilisation de fractions rationnelles simples paraît plus commode qu’une utilisation de fonctions de type exponentiel.

Existe-t-il une relation entre les modèles pluie-débit au pas de temps pluriannuel ?Does a link exist between rainfall-runoff models at the interannual time step?

Résumé

Abstract

1. Introduction