Article body

Introduction

Les enfants de milieu socioéconomiquement faible risquent de ne pas avoir acquis une représentation intuitive des nombres quand ils arrivent au primaire, ce qui joue en défaveur des apprentissages scolaires (Fuchs, Fuchs et Karns, 2001 ; Griffin, Case et Siegler, 1994). Les recherches suggèrent l’intérêt que revêt pour les enfants le soutien de leurs parents dans l’apprentissage de la ligne numérique, une compétence fondamentale pour aborder l’arithmétique. Plusieurs chercheurs et praticiens ont constaté que, dans les milieux de faible statut socioéconomique (SSE), le degré d’engagement des parents envers les apprentissages de leur enfant, la stimulation et l’encouragement qu’ils leur procurent favorisent un meilleur départ scolaire (Brooks-Gunn, Berlin et Fuligni, 2000 ; Miedel et Reynolds, 1999). Cet article a pour but d’évaluer l’impact à court terme d’un volet parental inhérent à un programme d’éveil numérique offert aux enfants de milieu socioéconomiquement faible.

Contexte théorique

Bien qu’un faible SSE affecte grandement la qualité de vie de la plupart des membres d’une communauté défavorisée, il atteint particulièrement les enfants ; il figure d’ailleurs parmi les facteurs les plus souvent associés à l’échec scolaire (De Civita, Pagani, Vitaro et Tremblay, 2004 ; Duncan, Brooks-Gunn et Klebanov, 1994 ; Hickman, Greenwood et Miller, 1995 ; Pagani, Boulerice et Tremblay, 1997 ; Pagani, Boulerice, Tremblay et Vitaro, 1999). Nous savons, par ailleurs, que de piètres résultats académiques à l’élémentaire (Nagin, Pagani, Tremblay et Vitaro, 2003) peuvent amorcer une longue suite de difficultés scolaires, comportementales et sociales (Pagani, Tremblay, Vitaro, Boulerice et McDuff, 2001), d’où le fréquent recours des enfants de milieu socioéconomiquement faible aux services d’éducation spécialisée et, plus tard, leur forte représentation parmi les décrocheurs et les délinquants (Hertzman et Wiens, 1996 ; Weikart et Schweinhart, 1992). Adultes, nous les retrouvons souvent dans les emplois moins rémunérateurs ou dans la liste des bénéficiaires chroniques de l’aide sociale (McLoyd, 1998), situation qui risque de se perpétuer de génération en génération.

Des différences frappantes peuvent distinguer l’environnement familial des enfants de milieu socioéconomiquement faible de ceux des milieux dont le SSE se trouve plus élevé (Bornstein et Bradley, 2003 ; Brooks-Gunn, Klebanov et Liaw, 1995 ; Evans, 2004 ; Jackson, 2003). Entre autres, les parents de faible SSE tendent à moins s’impliquer dans l’éducation de leur enfant que les parents plus fortunés (Feuerstein, 2000 ; Grolnick, Benjet, Kurowski et Apostoleris, 1997 ; Marcon, 1999). Les ressources psychologiques, sociales et physiques des premiers sont souvent limitées, ce qui ne peut que jouer contre un engagement efficace dans des activités cognitives stimulantes avec leur jeune enfant. Les parents de classes sociales plus avantagées, pour leur part, ont habituellement obtenu de meilleures performances scolaires durant leur enfance ; ils maîtrisent par conséquent de meilleures habiletés sociales et jouissent de ressources intellectuelles suffisantes pour interagir sereinement et efficacement avec le système scolaire (Alexander, Entwisle et Bedinger, 1994 ; Holloway, Rambaud, Fuller et Eggers-Piérola, 1995).

L’ouvrage de Lahire (1995) explore ce qui, dans différentes configurations familiales, favorise la réussite ou l’échec scolaire des enfants de milieux populaires. L’idée que les milieux socioéconomiquement faibles soient frappés d’une démission parentale par rapport à l’école serait un mythe. Cela dit, les parents de faible SSE ne nourrissent pas moins souvent un grand intérêt envers l’éducation de leur enfant (Epstein et Dauber, 1991) que les parents de SSE plus élevé. En effet, la vaste majorité d’entre eux accorde une grande importance à la scolarité de leur enfant (Lahire, 1995), mais plusieurs doutent de leurs propres compétences pour le soutenir sur ce plan (Pena, 2000). Il serait donc faux de présumer chez eux un manque d’intérêt ou l’absence d’objectifs scolaires ; ce qui leur fait défaut, ce sont plutôt les ressources nécessaires pour assurer un soutien efficace dans les apprentissages (De Civita et al., 2004). De plus, Lahire (1995) maintient que le soutien moral, affectif et symbolique des parents pour leur enfant apparaît d’autant plus important que les atouts familiaux sont faibles.

Pour contrer la vulnérabilité des familles de milieu socioéconomiquement faible et favoriser l’égalité des chances en éducation, plusieurs programmes d’intervention préventive sont destinés aux enfants et/ou aux familles de faible SSE. Inspiré par les programmes américains Head Start qui visent à promouvoir la performance scolaire et l’adaptation sociale des enfants de familles de faible SSE, le programme Opération Solidarité a été implanté à Montréal en 1970 (Commission des écoles catholiques de Montréal, 1994). On attendait de ce programme qu’il aide les enfants de milieu socioéconomiquement faible à développer les habiletés d’adaptation requises pour passer harmonieusement de l’éducation préscolaire à l’école primaire. À long terme, on espérait qu’il contribue à prévenir les effets néfastes souvent associés à la pauvreté.

Dans le contexte préscolaire, Opération Solidarité offre aux enfants de quatre ans un programme de prématernelle à demi-temps et un programme de maternelle à plein temps aux enfants de cinq ans. La cinquième et plus récente version du programme repose sur l’approche cognitive et mise sur le partenariat parents/enseignant/direction scolaire. Tout comme la plupart des interventions préventives en ce domaine, ce programme ne tient pas formellement compte des habiletés préalables aux apprentissages en arithmétique prévus en première année. Pourtant, c’est sur l’arithmétique que repose l’algèbre qui gouverne les lois des champs spécifiques en mathématiques dont la géométrie, la trigonométrie, le calcul, la transformation, etc.

Habiletés numériques et classe sociale

En Amérique du Nord, une vaste proportion d’enfants issus de familles à faible revenu ne franchissent pas la maternelle munis de la structure cognitive centrale requise pour réussir en arithmétique dès la première année (Arnold, Fisher, Doctoroff et Dobbs, 2002 ; Entwisle et Alexander, 1990 ; Fuchs et al., 2001 ; Griffin et Case, 1996 ; Pagani, Larocque, Tremblay et Lapointe, 2003 ; Starkey et Klein, 2000). Comme le signalent les théories du développement, les jeunes enfants devraient percevoir le système numérique comme un concept dimensionnel, c’est-à-dire une ligne mentale numérique qui, précisément, leur permettra d’appliquer les stratégies arithmétiques appropriées (Case et Sowder, 1990 ; Griffin et al., 1994). Or la faculté de structurer divers éléments fait plus ou moins défaut chez un certain nombre d’enfants qui amorcent leur première année scolaire : certains d’entre eux maintiennent une conception prédimensionnelle des nombres qui les porte à utiliser des stratégies inappropriées en addition et en soustraction (Case, 1975 ; Doherty, 1997) et, de surcroît, les empêche d’élaborer d’autres stratégies plus efficaces (Fuson, 1992). C’est pourquoi, parmi ces enfants, plusieurs n’atteignent pas leur plein potentiel et éprouvent des difficultés en arithmétique (Reyes et Stanic, 1988). Une vaste étude prospective réalisée au Québec (Pagani et al., 2001) montre que les difficultés en mathématiques expliquent près de la moitié des échecs scolaires des enfants provenant surtout de milieu socioéconomiquement faible[1].

L’écart de performance observé en milieu scolaire entre les enfants provenant de différentes couches socioéconomiques correspond fréquemment au décalage des connaissances intuitives normalement acquises à l’âge préscolaire en termes de précurseurs cognitifs en arithmétique. Aux yeux de certains adultes, les différents champs des mathématiques relèvent de la notation et du symbolisme. Aussi n’accordent-ils que peu d’attention aux enfants d’âge préscolaire eu égard à ce domaine, même s’il apparaît de plus en plus clairement que ces derniers sont tout naturellement disposés à développer la structure cognitive informelle qui prépare l’apprentissage formel ultérieur des champs mathématiques spécifiques (Greenes, 1999 ; National Council of Teachers of Mathematics, 2000 ; Pappas, Ginsburg et Jiang, 2003). Quoi qu’il en soit, l’apprentissage informel de la ligne numérique (concevoir l’ampleur relative, compter, additionner à l’aide d’objets concrets) s’élabore considérablement durant les années préscolaires (Starkey et Klein, 2000) ; les enfants stimulés dès leur jeune âge, constate-t-on de plus en plus, montrent une gamme impressionnante d’habiletés numériques quand ils arrivent à l’école (Fuson, 1992 ; Carpenter, Ansell, Franke, Fennema et Weisbeck, 1993).

La compréhension numérique de l’enfant d’âge préscolaire dépasse le simple fait de pouvoir énumérer la séquence des chiffres ou de les reconnaître (Klein et Bisanz, 2000). De fait, ces connaissances informelles en mathématiques se traduisent également par la connaissance des nombres (compter des objets, comparer deux ensembles d’objets et déterminer s’il y en a plus, moins ou autant), la reconnaissance des formes (géométrie), le raisonnement spatial (remplir et vider, décrire les directions et les distances dans un espace de jeu) (Clements, Swaminathan, Hannibal et Sarama, 1999 ; Newcombe et Huttenlocher, 2000), la reconnaissance de l’ampleur relative (contrastes, oppositions, pairs et impairs, fractions), la résolution de problèmes arithmétiques (addition, soustraction), la classification (similarités et différences, tri des objets, distinction et description des formes) (Baroody, 1992 ; Starkey et Cooper, 1995), les couleurs (pour la classification), la sériation (comparaison des caractéristiques des objets : plus gros/plus petit) et finalement, le rapport au temps (comparer des intervalles de temps, anticiper et décrire la séquence des événements). Ces concepts préalables forment le noyau du système numérique et fournissent une base pour l’acquisition, la compréhension et l’assimilation éventuelle des mathématiques enseignées dans le contexte scolaire (Geary, 1994 ; Ginsburg, 1989).

Les résultats du programme Head Start indiquent que certains parents de faible SSE inscrits dans ce programme américain n’offrent à leur enfant que peu de soutien en matière d’habiletés numériques (Klein et Starkey, 1995), contribuent significativement moins aux activités reliées aux chiffres et favorisent des activités moins complexes que les activités promues par les parents plus fortunés (Saxe, Guberman et Gearhart, 1987). Contrairement aux parents de SSE élevé, les parents moins scolarisés et issus des minorités visibles recourent plus volontiers à des méthodes formelles qu’au jeu pour encourager l’apprentissage chez leur enfant (Powell, 1994 ; Stipek, Milburn, Clements et Daniels, 1992).

McDill et Natriello (1999) insistent sur l’importance d’encourager les parents et les enseignants à utiliser des techniques d’enseignement informel pour favoriser, surtout auprès des enfants de faible SSE, les apprentissages de la ligne numérique. Peu d’enfants inscrits à la maternelle bénéficient d’un programme d’éveil aux différentes manifestations du système numérique. Ceux qui en bénéficient développeront pourtant, en première année, une meilleure compréhension des nombres (Arnold et al., 2002), d’efficaces habiletés numériques (Griffin, Case et Pick, 1998) et un intérêt pour les apprentissages à venir dans ce domaine (Stevenson et Newman, 1986).

Programme d’éveil numérique Righstart

À la suite de résultats peu encourageants obtenus au cours d’une recherche auprès des jeunes de faible SSE sur la connaissance des nombres (Case, 1975 ; Case, Griffin et Kelly, 2001), Case et Griffin ont mis sur pied, durant les années 1980, une intervention destinée aux enfants vulnérables à cet égard, dans le but de les préparer au premier apprentissage formel en cette matière (Griffin, Case et Carpenter, 1994). Le programme Rightstart, basé sur divers jeux interactifs d’apprentissage, donne la possibilité aux enfants de milieux socioéconomiquement faibles inscrits en maternelle d’acquérir dès cette étape les concepts préalables (couleurs, formes et quantités) à l’apprentissage de la ligne numérique et ce, selon un rythme logique et progressif. L’objectif fondamental de ce programme vise à promouvoir chez les enfants la relation entre l’univers des nombres et l’univers de la quantité, ce qui les amène à saisir que les nombres ont un sens et permettent de prédire ou d’expliquer logiquement la réalité.

L’efficacité de ce programme a été établie au Canada et aux États-Unis auprès des enfants de maternelle qui proviennent de divers milieux linguistiques et culturels, de niveau d’appartenance socioéconomique faible et moyen (Griffin et Case, 1996). Les enfants bénéficiaires ont pu développer une compréhension conceptuelle des nombres significativement supérieure (Griffin, Case et Capodilupo, 1995 ; Case et al., 2001) à celle du groupe témoin. À la fin de la maternelle, ces enfants avaient également rattrapé le retard observé dans leur connaissance des nombres par rapport à leurs pairs de classe socioéconomique moyenne (Griffin et Case, 1997).

Au cours des dernières années, la traduction, l’adaptation et l’implantation du programme Rightstart ont été effectuées, en collaboration avec Case, dans les maternelles francophones de Montréal situées en milieux socioéconomiquement faibles. Pagani, Jalbert et Girard (2006) souhaitaient non seulement augmenter les chances des enfants démunis d’acquérir les concepts préalables aux opérations de soustraction et d’addition, mais également de diminuer la probabilité de nombreux échecs scolaires et de difficultés d’adaptation au cours de leur trajectoire scolaire. Les activités (58 jeux d’apprentissage) appliquées en classe de maternelle permettaient aux enfants de construire et de consolider les concepts numériques sur une période de quatre mois. Les résultats de la première cohorte témoignent de l’efficacité du programme. En effet, on remarque une différence significative quant à la connaissance des nombres en faveur des enfants soumis à un plus grand nombre d’activités du programme, comparativement aux enfants ayant reçu un moindre dosage ou à ceux du groupe témoin n’ayant pas participé. Pagani et ses collaborateurs (2006) ont alors mis en évidence la nécessité d’administrer un dosage élevé du programme d’éveil numérique aux enfants de milieu socioéconomiquement faible.

Les programmes qui offrent un plus fort dosage ou ajoutent des volets, par exemple la participation des parents, produisent de meilleurs gains (Rutter, 2002), apparemment plus durables (Ramey et Ramey, 1992). La plupart des interventions comportent incidemment plusieurs volets. Toutefois, malgré que cela détienne une certaine importance, il est rarement précisé lequel de ces volets influence le plus la différence observée entre les groupes. Selon Rutter, les chercheurs devraient évaluer le facteur spécifique que représente l’environnement, lequel contribue à l’efficacité de l’intervention. Autrement dit, il s’agirait de savoir dans quelle mesure telle modification de l’intervention s’associe de façon systématique aux changements observés dans la réponse obtenue.

Implication des parents

Très peu de programmes d’intervention visent le soutien des parents et leur collaboration au développement des précurseurs cognitifs en arithmétique. D’ailleurs, peu d’efforts semblent déployés en faveur de l’apprentissage informel de la ligne numérique dans la population préscolaire de faible SSE (Starkey et Klein, 2000). Jusqu’à présent, les programmes préscolaires axés sur les concepts préalables à l’arithmétique ont davantage ciblé l’enseignant pour jouer le rôle de transmetteur de la connaissance des nombres aux enfants ; de toute évidence, la participation éventuelle des parents à cet égard semble plutôt avoir été négligée.

La participation des parents aux apprentissages académiques devient une composante majeure de plusieurs réformes scolaires (Comer, 1996) et de plusieurs programmes de prévention primaire en milieu socioéconomiquement faible (Campbell et Taylor, 1996 ; Washington et Bailey, 1995 ; Zigler et Muenchow, 1992). À plusieurs reprises, il a été démontré que la participation des parents dans l’éducation de leur enfant (Hoover-Dempsey et Sandler, 1997 ; Reynolds, 1989) et un environnement familial stimulant (Brooks-Gunn et al., 2000) favorisent sa réussite scolaire. Cependant, la littérature sur le sujet concerne presque exclusivement l’école primaire ; conséquemment, il serait nécessaire d’étudier les effets de la participation parentale promue par les programmes de prévention au niveau préscolaire (Lamb-Parker, Piotrkowski, Baker, Kessler-Sklar, Clark et Peay, 2001).

Head Start est tenu pour le premier modèle bigénérationnel de soutien aux jeunes enfants et à leur famille (Parker, Piotrkowski, Horn et Greene, 1995). La participation active des parents a toujours été une composante majeure de ce programme. Par contre, très peu de recherches empiriques se sont intéressées à l’impact spécifique de cet aspect sur les résultats obtenus (Taylor et Machida, 1994), ce qu’on peut également reprocher à l’ensemble de la littérature qui tend à évaluer la participation parentale dans une optique qualitative et non empirique.

En outre, des quelques recherches empiriques sur la participation parentale se dégagent des résultats controversés (Fan et Chen, 2001) : aucune preuve ne peut encore permettre de conclure à un effet essentiel de la participation parentale sur le succès des interventions préventives et le maintien de leurs effets chez les enfants de milieu socioéconomiquement faible (Miedel et Reynolds, 1999). Alors que, dans l’application d’un programme préventif, certains chercheurs observent une relation positive entre la participation des parents, les acquis préalables aux apprentissages du primaire et le rendement scolaire ultérieur de l’enfant (Henderson et Berla, 1994 ; Marcon, 1999 ; Reynolds, Mavrogenes, Bezruczko et Hagemann, 1996 ; Singh, Bickley, Trivette, Keith, Keith et Anderson, 1995), d’autres ne constatent que peu d’effets, sinon aucun (Barnett, Young et Schweinhart, 1998 ; Bobbett, 1995 ; White, 1985 ; White, Taylor et Moss, 1992). D’ailleurs, ces auteurs croient que les arguments et les politiques en faveur de la participation des parents débordent bien souvent les preuves scientifiques jusqu’ici établies.

Nous sommes donc en face, d’une part, d’un intérêt croissant pour la participation des parents aux interventions préventives et, d’autre part, de conclusions incertaines quant à ses effets. Nous devons donc en déduire que tous les types de participation parentale ne donnent pas forcément des résultats d’égale valeur ; il apparaît donc évident qu’il faut éviter de promouvoir un type particulier de participation parentale.

Objectif et hypothèse

Cet article a pour but d’examiner la valeur ajoutée d’un volet parental introduit dans le programme préventif Rightstart, centré sur l’acquisition des concepts préalables en arithmétique au cours de la période préscolaire. La composante parentale du programme a été offerte à un échantillon d’enfants qui profitaient déjà du programme dans le contexte des classes de maternelle. Selon les conclusions de Rutter (2002), il était attendu que la participation des enfants au programme, à laquelle s’ajoutait celle de leurs parents (dosage théoriquement plus élevé), se traduise, chez les enfants, par une meilleure connaissance des nombres à la fin de la maternelle, comparativement : 1) aux enfants qui bénéficiaient du programme en classe sans la participation de leurs parents (un dosage théoriquement plus faible) ; et 2) aux enfants qui bénéficiaient du programme en classe et dont les parents ne se sont jamais présentés aux ateliers auxquels ils s’étaient pourtant inscrits (un dosage théoriquement plus faible).

Méthodologie

Participants et déroulement

En 1997-2000, une vaste étude longitudinale prospective a été lancée afin d’évaluer différentes composantes du programme préscolaire Opération Solidarité (OS), offert dans les écoles primaires francophones de la Commission Scolaire de Montréal (CSDM). Notre étude se compose d’un échantillon d’enfants issus des quartiers socioéconomiquement faibles de Montréal (n = 524) et ayant débuté la maternelle en septembre 1999. L’échantillon a été formé après avoir obtenu successivement le triple consentement de la direction des écoles, des enseignants et des parents.

Au début de l’année scolaire 1999-2000, des lettres ont été acheminées à la direction des écoles qui offraient le programme préscolaire OS, afin de solliciter la participation des classes de maternelle au programme préventif d’enrichissement des précurseurs cognitifs numériques Rightstart (RS). À la suite de l’autorisation des écoles, les enseignants devaient, à leur tour, consentir ou non à participer à une formation sur le programme RS et à implanter le programme dans leur classe. Au total, 11 écoles ont accepté de participer au programme RS, ce qui représente des classes de maternelle dirigées par 28 enseignants. Tous les enfants de cette cohorte ont donc reçu le programme traditionnel OS dans leur classe de maternelle et 73,7 % de cet échantillon (189 garçons, 197 filles, âge moyen = 5,67) ont également reçu le programme d’éveil numérique dans leur classe, de janvier à mai 2000.

À l’hiver 2000, la direction des écoles et les enseignants consentants étaient informés, par courrier, de l’ajout d’un volet parental au programme. Ils étaient alors avisés de la possibilité d’offrir à leur école différents ateliers pour initier les parents au programme RS. Quand la direction des écoles et les enseignants appuyaient l’application du volet parental dans leur école, les enseignants étaient invités à faire parvenir une lettre aux parents (n = 254) pour obtenir leur consentement, leurs disponibilités et les informer de ces ateliers qui allaient se dérouler uniquement en français. Les parents ayant donné leur consentement par écrit (n = 165, donc 65 % des parents sollicités) ont ensuite été contactés par téléphone afin qu’on leur explique le déroulement général des ateliers-parents et qu’on vérifie leur intention de participer aux rencontres. Dans le but de maximiser la participation des parents aux ateliers, il était permis à la mère et/ou au père d’assister aux rencontres.

Au total, 109 enfants (58 garçons, 51 filles) provenant de sept écoles ont reçu la composante parentale du programme RS, ce qui totalise 28,2 % des enfants qui profitaient déjà du programme RS à la maternelle. Malgré le consentement formel de leurs parents à participer aux ateliers, 54 enfants (20 garçons, 34 filles) n’ont jamais reçu la composante parentale du programme faute de voir leurs parents se présenter aux rencontres. Les principaux obstacles à leur présence tenaient à des difficultés de langue ou encore à des conflits d’horaire.

Des données complètes étant disponibles pour 358 enfants de l’échantillon original, ces derniers ont été retenus pour fins d’analyses statistiques : 201 enfants (51,2 % de garçons) ont participé en classe au programme d’éveil numérique Rightstart (groupe de comparaison RS) ; 51 enfants (37,3 % de garçons) ont participé en classe au programme RS et, bien que leurs parents s’étaient portés volontaires, ceux-ci ne se sont jamais présentés aux ateliers qui leur étaient destinés (groupe de comparaison CC) ; et enfin, 106 enfants (51,9 % de garçons) ont participé en classe au programme RS en plus de se prévaloir du volet parental du programme (groupe expérimental RS/CP).

L’âge moyen de l’échantillon était de 5,65 ans à l’automne 1999. La majorité provenait d’un milieu socioéconomiquement faible ; en moyenne, 68,6 % des familles concernée disposaient d’un revenu annuel inférieur aux seuils de faible revenu, tels que définis par Statistique Canada (2002). L’échantillon était aussi constitué d’un nombre important d’allophones : environ un tiers des enfants (34,6 %) parlaient une langue maternelle autre que le français.

Les enfants ont été évalués individuellement à deux reprises par un assistant de recherche :

  • une première fois à l’automne 1999 (prétest), avant l’implantation du programme ;

  • une seconde fois au printemps 2000 (post-test), à la suite de leur participation au programme.

Tous les enseignants, parents et enfants étaient informés qu’ils pouvaient à tout moment se retirer de l’étude.

Rightstart/composante parentale (RS/CP)

Le volet parental du programme RS vise non seulement à introduire, à respecter et à renforcer les concepts enseignés par RS aux enfants du niveau de la maternelle, mais aussi à rendre les parents conscients de leur rôle d’éducateur, de stimulateur et d’agent susceptible de bonifier le programme. Plus spécifiquement, les ateliers-parents visent à : 1) sensibiliser les parents aux capacités dont ils disposent pour stimuler et renforcer le développement des précurseurs cognitifs de la ligne numérique chez leur enfant ; 2) les encourager à reconnaître les progrès de leur enfant ; 3) promouvoir la relation entre les parents et les enseignants afin d’accentuer la complémentarité entre l’école et la famille ; 4) offrir aux parents un certain soutien concernant la stimulation cognitive ; et 5) intégrer la pensée générale mathématique dans la vie quotidienne des parents et de l’enfant, jusqu’à l’automatisme.

Les ateliers-parents s’échelonnaient sur une période de quatre mois, à raison d’une rencontre par mois (d’une durée d’une heure trente) et se déroulaient durant la deuxième moitié de l’année scolaire (de mars à juin 2000), à peu près au même moment qu’était implanté en classe le programme RS. Ces ateliers réunissaient une intervenante, le groupe de parents (groupes variant entre 11 et 26 parents) et leurs enfants. Bien qu’encouragés à participer au volet parental, la présence des enseignants à ces ateliers était à leur discrétion.

Les ateliers-parents étaient animés par deux assistantes de recherche inscrites aux études supérieures en psychologie et en psychoéducation : l’une d’elle est l’auteure principale de l’article ; elle a participé à l’élaboration du volet parental et veillé à former l’autre intervenante qui, pour sa part, avait acquis de l’expérience auprès des jeunes enfants et des familles de milieu socioéconomiquement faible. L’année précédant l’élaboration et l’implantation du volet parental, ces intervenantes avaient également implanté le programme RS auprès d’une autre cohorte d’enfants du niveau de la maternelle. Elles étaient donc familières avec le programme offert en classe.

Les écoles ont été réparties de façon aléatoire entre les deux intervenantes. Chacune a pris soin de téléphoner à tous les parents et enseignants concernés avant chaque atelier pour leur rappeler le moment et le lieu de la rencontre. Les intervenantes devaient également rédiger un cahier de bord après chaque atelier afin de fournir de l’information pertinente sur la mise en oeuvre du programme. Le cahier de bord rédigé après chaque atelier fournissait de l’information sur les conditions de réalisation des activités, sur l’ampleur de la participation au programme, sur l’atteinte des objectifs et sur la qualité de la participation elle-même. Il rendait compte également des modifications majeures apportées à l’intervention, des commentaires et des critiques concernant l’implantation et le contenu des ateliers, des difficultés de parcours, etc. Les intervenantes devaient également noter la durée de chaque atelier.

Ateliers. Concrètement, les quatre ateliers se déroulaient de la façon suivante : les deux premiers ateliers étaient destinés exclusivement aux parents (sans la présence de leur enfant) pour les familiariser avec le programme RS. Durant ces deux rencontres, les bases théoriques du programme de même que certaines notions sur le développement cognitif du jeune enfant (périodes de développement de l’intelligence selon Jean Piaget, développement de la ligne mentale numérique, etc.) étaient présentées aux parents suivant une méthode interactive.

Au cours des deux premières rencontres étaient aussi présentées chacune des 11 unités du programme et le matériel nécessaire aux activités. Une bande-vidéo montrait des enfants de maternelle en activité dans le cadre du programme RS. Du matériel (photocopies de certaines activités RS réalisées en classe ; suggestions d’activités à la maison favorables à l’éveil numérique) leur était également remis. Il était fortement conseillé aux parents d’assister aux deux premiers ateliers, s’ils voulaient profiter pleinement des rencontres subséquentes.

Les deux derniers ateliers requéraient la participation conjointe des parents et des enfants autour d’activités précisément conçues pour stimuler l’éveil numérique. Il s’agissait pour les parents d’agir avec l’enfant, de l’observer dans ses apprentissages et d’interagir favorablement avec lui. Chacun de ces deux ateliers comportait deux activités individuelles (parent/enfant) et une activité en sous-groupe (petite équipe formée de deux dyades). Au début de chaque activité, l’intervenante faisait une démonstration aux dyades tout en présentant la façon de disposer le matériel. L’intervenante suggérait également aux parents différentes façons de vérifier la compréhension que montrait leur enfant de certains concepts reliés à l’arithmétique, par exemple à l’aide de questions telles que : « Qui est le plus près de gagner la partie ? » et « Comment le sais-tu ? ».

Lors du troisième atelier, les consignes étaient principalement énoncées aux enfants afin qu’ils parviennent par la suite à les transmettre à leurs parents. Les jeux interactifs à cet égard proviennent du répertoire des activités de RS, auxquelles ils avaient été initiés en classe[2]. Lors du quatrième atelier, les consignes étaient principalement énoncées aux parents, mais toujours dans un langage adapté au niveau de l’enfant afin que ce dernier puisse tout de même comprendre les consignes de l’intervenante. Une fois le matériel distribué, les parents présentaient alors à nouveau la tâche à leur enfant, en respectant les consignes initiales. Contrairement à celles du troisième atelier, ces activités n’avaient pas été présentées aux enfants en classe et relevaient d’une plus grand complexité[3]. Enfin, lors du dernier atelier, les parents étaient invités à évaluer les ateliers-parents par écrit.

Instruments de mesure : variables indépendantes

Certaines informations (revenu familial et souci parental de la réussite scolaire) ont été recueillies à partir du questionnaire complété par les parents, incidemment identique à celui qui se trouve utilisé dans L’Enquête longitudinale nationale sur les enfants et les jeunes (ELNEJ) (Statistique Canada, 1995). Le résultat obtenu au prétest du Test de connaissance des nombres (NKT) et les conditions du programme d’éveil numérique (RS ; RS/CP ; CC) ont également été introduites à titre de variables indépendantes dans cette étude.

Revenu familial. Il s’agit d’une variable continue représentée sur une échelle de 1 à 13, indiquant différentes catégories de revenu familial total, en milliers de dollars canadiens : 1) moins de 5 ; 2) 5-9,9 ; 3) 10-14,9 ; 4) 15-19,9 ; 5) 20-24,9 ; 6) 25-29,9 ; 7) 30-34,9 ; 8) 35-39,9 ; 9) 40-44,9 ; 10) 45-49,9 ; 11) 50-54,9 ; 12) 55-59,9 ; et 13) 60 et plus.

Souci de la réussite scolaire. Cette variable continue est révélée par la réponse des parents à la question : « Dans quelle mesure est-ce important pour vous que votre enfant obtienne de bonnes notes à l’école ? » – 1) Très important ; 2) Important ; 3) Peu important ; et 4) Pas important.

Prétest : Test de connaissance des nombres. Ce test relève d’une adaptation en langue française du Number Knowledge Test (NKT) (Okamoto et Case, 1996). Traduit en collaboration avec Case, il évalue la connaissance intuitive des nombres et de la quantité ou, en d’autres termes, l’étendue des connaissances acquises par l’enfant compte tenu de son niveau d’âge (Okamoto et Case, 1996 ; Griffin et al., 1995 ; Griffin, Case et Sandieson, 1992 ; Griffin, Case et Siegler, 1994). Le test est subdivisé en cinq niveaux correspondant aux connaissances habituelles en mathématiques des enfants de 4, 6, 8, 10 et 12 ans, dont le développement est jugé « normal ». Lors du prétest, un maximum de 19 items ont été administrés afin de mesurer les précurseurs cognitifs suivants : 1) la connaissance de la séquence des chiffres de 1 à 10 ; 2) la compréhension de la correspondance terme à terme entre les chiffres et les objets ; 3) la compréhension de la valeur cardinale de chaque chiffre ; 4) la compréhension de la règle générative qui relie les valeurs cardinales adjacentes ; et 5) la compréhension que chaque chiffre qui se succède représente un ensemble comprenant plus d’objets. Ces habiletés constituent toutes des prédicteurs de performance en arithmétique.

Chaque item du NKT est lu oralement et requiert une réponse orale de la part de l’enfant. Le résultat total représente le nombre de problèmes réussis correctement jusqu’à ce que l’enfant ne puisse plus répondre à tel niveau de questions. L’administration du test et le calcul des résultats prennent environ 15 minutes. Des normes ont été échelonnées sur des niveaux d’âge de 4 ans à 10 ans pour les enfants issus des milieux socioéconomiquement faible et moyen de l’Ontario, du Massachusetts, de l’Oregon et de la Californie. Les normes établies chez 6000 enfants francophones du Québec (Tremblay, Lapointe, Hébert, Boulerice, Girard, Pagani et Vitaro, 2000) sont similaires à celles que présentent Okamoto et Case (1996). Le prétest du NKT a été administré individuellement au début de la maternelle (automne 1999) par un assistant de recherche expérimenté avec ce test.

Conditions du programme d’éveil numérique. Deux variables dichotomiques indiquent le programme dont l’enfant a bénéficié : 1) le programme RS et le volet parental du programme (RS/CP = 0) ou le programme RS uniquement (RS = 1) ; et 2) le programme RS et le volet parental du programme (RS/CP = 0) ou le programme RS uniquement, mais en tenant compte de l’intérêt manifesté par les parents pour assister au volet parental, même s’ils ne se sont jamais présentés aux ateliers (CC = 1).

Mesure : variable critère

Post-test : Test de connaissance des nombres. Il s’agit d’une variable continue représentant le résultat obtenu par l’enfant à la suite de l’implantation du programme RS et du volet parental (printemps 2000). Le score minimum pouvant être obtenu est 0 et le résultat maximum est 19. Le post-test du NKT a été administré individuellement par un assistant de recherche expérimenté avec ce test.

Démarche analytique

Les analyses statistiques effectuées ont pour but de vérifier l’hypothèse de départ, voulant que la participation des parents dans le programme RS (groupe RS/CP) soit associée, chez les enfants de milieu socioéconomiquement faible, à une plus grande connaissance des nombres à la fin de la maternelle comparativement aux enfants qui ont participé au programme sans la collaboration de leurs parents (groupes RS et CC). L’analyse de régression multiple hiérarchique et le calcul de l’ampleur de l’effet de l’intervention ont permis de vérifier cette hypothèse. Préalablement à ces analyses, des statistiques descriptives ont été utilisées pour définir les trois groupes à l’étude (RS, CC, RS/CP) et des analyses préliminaires ont été conduites. Le seuil statistique a été fixé à p < 0,05 pour toutes les analyses, ce qui, selon Tukey (1991), reflète une approche conservatrice, puisque le seuil acceptable pour évaluer les effets principaux des analyses préliminaires peut être fixé jusqu’à p < 0,15.

Résultats

Statistiques descriptives

Le Tableau 1 présente les moyennes et les écarts-type des variables continues et le pourcentage des variables dichotomiques pour les enfants et les familles du groupe RS, du groupe CC et du groupe RS/CP. Du point de vue des moyennes, les enfants du groupe RS/CP sont significativement plus avantagés (prétest du NKT ; revenu familial ; importance accordée à la réussite scolaire ; post-test du NKT) que leurs pairs des deux groupes de comparaison (RS et CC). Les enfants du groupe CC, pour leur part, semblent les plus désavantagés de l’échantillon.

Tableau 1

Caractéristiques des échantillons : moyennes, écarts-type et pourcentages

Caractéristiques des échantillons : moyennes, écarts-type et pourcentages

Note : Les écarts-types sont indiqués entre parenthèses ; NKT = Test de connaissance des nombres ;

n.s. = non significatif.

-> See the list of tables

Analyses préliminaires

Les variables utilisées pour définir les groupes qui seront utilisés dans l’analyse du modèle final découlent d’analyses préliminaires effectuées entre diverses variables et la variable critère. Seules les variables reliées significativement à la variable critère ont été retenues. Après les analyses de variance unifactorielle (ANOVA) effectuées, des tests de comparaisons multiples a posteriori (test de Scheffé) ont permis d’identifier que les trois groupes de l’étude diffèrent significativement entre eux quant au prétest du NKT, du revenu familial et du post-test du NKT. Plus précisément, les enfants du groupe RS/CP se différencient favorablement de ceux du groupe RS (prétest du NKT, p = 0,03 ; revenu familial, p = 0,05 ; et post-test du NKT, p < 0,001), en plus de se différencier favorablement du groupe CC (prétest du NKT, p = 0,003 ; revenu familial, p = 0,001 ; et post-test du NKT, p = 0,009). Une différence significative est également observée entre le groupe RS et le groupe RS/CP, avec les parents du groupe RS qui se soucient davantage de la réussite scolaire de leur enfant (p = 0,05) que les parents ayant participé au programme (RS/CP).

Des matrices de corrélations partielles ont été calculées entre les variables prédictives du Tableau 1 et la variable critère (post-test du NKT), en contrôlant pour le résultat obtenu par l’enfant au prétest du NKT ; nous remarquons ainsi que des associations significatives au niveau statistique sont présentes entre la variable critère et certaines variables prédictives. Plus précisément, les enfants qui obtiennent de meilleurs résultats au post-test du NKT vivent dans une famille avec un revenu plus élevé (r = 0,13, p = 0,02) et ont des parents qui accordent moins d’importance à la réussite scolaire de leur enfant (r = 0,17, p = 0,007). Toutefois, le sexe, la langue maternelle, l’âge de l’enfant et la scolarité maternelle ne sont plus corrélés de façon significative avec le résultat obtenu au post-test du NKT.

Étant donné l’association significative de certaines variables prédictives (prétest du NKT, revenu familial et souci parental de la réussite scolaire) avec la variable critère (post-test du NKT) et étant donné certaines différences significatives observées entre les groupes sur ces mêmes variables prédictives, nous avons choisi d’en tenir compte dans l’analyse de régression multiple hiérarchique.

Analyses inférentielles

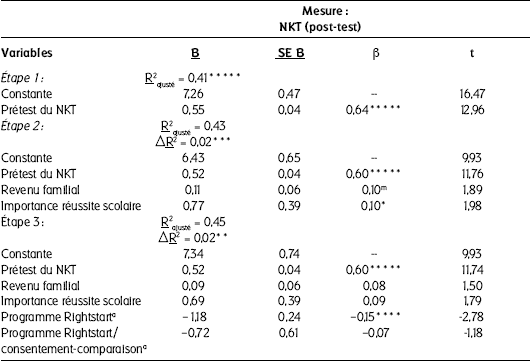
Une analyse de régression multiple hiérarchique en trois étapes a été employée pour examiner la valeur ajoutée de la composante parentale du programme d’éveil numérique RS sur la connaissance des nombres des enfants à la fin de la maternelle (post-test du NKT). Cela a été fait en contrôlant : 1) le résultat obtenu au prétest du NKT ; 2) le revenu familial et l’importance accordée à la réussite scolaire ; et 3) les conditions du programme (RS, CC et RS/CP). Les résultats de cette analyse sont présentés au Tableau 2.

Tableau 2

Résultats obtenus à chacune des étapes de l’analyse de régression multiple hiérarchique

Résultats obtenus à chacune des étapes de l’analyse de régression multiple hiérarchique

Note : aRightstart/composante parentale = 0 ; NKT = Test de connaissance des nombres ;mp = 0,06 ; * p = 0,05 ; ** p = 0,02 ; *** p = 0,01 ; **** p = 0,006 ; ***** p < 0,001.

-> See the list of tables

Dans la première équation, le résultat obtenu au prétest du NKT apporte une contribution significative au modèle (R2 = 0,41, Fvariation [1,240] = 168,07, p < 0,001). Environ 41,2 % de la variance de la connaissance des nombres à la fin de la maternelle (post-test du NKT) peut être attribuable à cette première variable. Un meilleur résultat obtenu au prétest du NKT est associé à une plus grande connaissance des nombres à la fin de la maternelle (t = 12,96, p < 0,001).

À la deuxième étape, les variables externes à l’enfant (revenu familial et importance accordée à la réussite scolaire) sont ajoutées afin de vérifier si ces variables réussissent à prédire la connaissance des nombres au post-test du NKT, au-delà de ce que peut prédire le résultat obtenu au prétest. Les résultats démontrent que ces variables prédictives y contribuent peu (2,0 %), même si elles représentent une variance additionnelle significative permettant de prédire le résultat obtenu au post-test du NKT (ΔR2 = 0,02, Fvariation [2,238] = 4,74, p = 0,01). À cette étape, le résultat obtenu au prétest du NKT et l’importance que les parents accordent à la réussite scolaire de leur enfant sont des prédicteurs significatifs. Un meilleur résultat obtenu au prétest du NKT est associé à une plus grande connaissance des nombres à la fin de la maternelle (t = 11,76, p < 0,001) et les parents qui accordent moins d’importance à la réussite scolaire ont des enfants qui démontrent une plus grande connaissance des nombres à la fin de la maternelle (t = 1,98, p = 0,05). Une association marginale est également observée entre le revenu familial et le résultat obtenu au post-test du NKT (t = 1,89, p = 0,06).

Enfin, comme troisième étape, les conditions du programme d’éveil numérique (groupe de référence : RS/CP) sont ajoutées aux variables prédictives des deux étapes précédentes. Les résultats indiquent que ce nouveau modèle explique une légère hausse de 2,0 % à la performance obtenue au post-test du NKT et permet donc d’améliorer très légèrement la prédiction effectuée au modèle précédent, (ΔR2 = 0,02, Fvariation (2,236) = 3,88, p = 0,02). Ces résultats révèlent que les conditions du programme, considérées conjointement, contribuent, bien que de façon minime, à prédire la performance obtenue au post-test du NKT, au-delà de ce que les variables prédictives des deux étapes précédentes peuvent expliquer. À cette étape, le résultat au prétest du NKT (t = 11,74, p < 0,001) demeure significatif. L’importance accordée à la réussite scolaire et le revenu familial ne contribuent pas à prédire de façon unique le résultat obtenu au post-test du NKT. Avec toutes les variables inclues dans le modèle, 45,2 % de la variance de la connaissance des nombres à la fin de la maternelle (post-test du NKT) est expliquée.

Les résultats obtenus à cette troisième étape permettent également d’avancer que, même après avoir contrôlé d’autres facteurs reliés à la connaissance des nombres, les enfants du groupe RS/CP obtiennent des résultats significativement supérieurs aux enfants du groupe RS, en obtenant 1,18 points de plus au post- test du NKT (sur une évaluation où le maximum de point accordés est de 19) (t = –2,78, p = 0,006). Aucune différence significative n’est toutefois observée au post-test du NKT (t = –1,18, p > 0,05) entre les enfants du groupe CC et ceux du groupe RS/CP.

Analyse de l’ampleur de l’effet

Lorsque l’hypothèse de recherche est évaluée via une analyse de régression multiple, il est souhaitable de rapporter l’ampleur de l’effet des prédicteurs (McCartney et Rosenthal, 2000). L’ampleur de l’effet fournit un indice standardisé qui permet d’apprécier l’ampleur du bénéfice de l’intervention, s’il y a lieu. Elle s’avère plus avantageuse que de résumer l’intervention à un choix binaire entre un effet significatif ou non significatif (Folger, 1989). Dans le modèle de régression multiple, l’ampleur de l’effet calculée est le « f2 de Cohen [4] ». Selon Cohen (1988), un f2 de :

  • 0,02 est petit ;

  • de 0,15 est modéré ;

  • de 0,35 est grand.

Dans notre étude, l’ampleur de l’effet de la variable prédictive « conditions du programme » a été établie à 0,03, ce qui, selon Cohen (1988), équivaut à une petite ampleur. Puisque l’analyse de régression multiple a démontré une différence significative dans la connaissance des nombres des enfants du groupe RS et du groupe RS/CP à la fin de la maternelle, l’ampleur de l’effet a été calculée pour ces deux groupes spécifiquement. L’ampleur de l’effet, établie à f2 = 0,03, représente une petite ampleur. La valeur du f2 peut également être transformée et interprétée en termes de proportion de la variance (R2), en divisant f2 par (1 + f2). Ainsi, un petit effet équivalent à 0,03 rend compte de 3 % (R2 = 0,029) de la variance expliquée au post-test du NKT, laquelle en termes de corrélation équivaut à R = 0,17.

Selon McCartney et Rosenthal (2000), l’ampleur de l’effet peut être calculée peu importe si une association significative est observée ou non. En conséquence, même si des résultats peu concluants ont été observés entre les groupes RS/CP et CC, l’ampleur de l’effet du groupe RS/CP sur la variable critère NKT a été calculée en comparaison avec le groupe CC. Cette ampleur de l’effet a été établie à 0,00, ce qui n’atteint pas le seuil d’une petite ampleur de l’effet.

Discussion

Cette étude avait pour but d’examiner si, en milieu socioéconomiquement faible, la participation conjointe des parents et de leur enfant au programme d’éveil numérique Rightstart produisait à court terme des effets positifs sur la connaissance des nombres des enfants. L’hypothèse voulait que les sujets qui bénéficiaient à la fois du programme en classe et de la participation de leurs parents aux ateliers afférents (RS/CP) démontreraient une meilleure connaissance de la ligne numérique à la fin de la maternelle que : (1) les enfants n’ayant bénéficié que du programme en classe (RS) ; et (2) les enfants ayant reçu le programme en classe et dont les parents ne se sont pas présentés aux ateliers auxquels ils s’étaient pourtant inscrits (CC).

Les analyses statistiques n’appuient que partiellement l’hypothèse de départ. Tout d’abord, à défaut d’établir de véritables liens de causalité entre les facteurs étudiés, les résultats permettent tout de même de constater une relation positive entre la participation parentale au programme et la connaissance des nombres chez les enfants à la fin de la maternelle et ce, compte tenu des éléments obtenus au prétest du NKT, du revenu familial et de l’intérêt parental à l’égard des résultats scolaires de leur enfant. L’ajout du volet parental au programme Rightstart semble avoir permis aux parents de stimuler le développement de la ligne numérique chez leur enfant et de favoriser chez lui une meilleure connaissance des nombres, comparativement aux sujets ayant suivi le programme sans la participation de leurs parents (RS). Un tel résultat souligne l’importance du dosage de l’intervention et montre que, si brève soit-elle et pourvu qu’elle soit bien centrée, l’intervention à dose plus élevée peut avoir des effets immédiats sur les enfants (Arnold, Lonigan, Whitehurst et Epstein, 1994 ; Whitehurst, Arnold, Epstein, Angell, Smith et Fischel, 1994).

Contrairement aux résultats d’autres études (Barnett et al., 1998 ; Bobbett, 1995 ; White, 1985 ; White et al., 1992), ce premier résultat pourrait indiquer que l’ajout d’une composante parentale au programme préventif dans le cadre préscolaire peut augmenter les chances des enfants de tirer profit de l’intervention. Cependant, la prudence est de mise puisque des résultats peu concluants quant à la connaissance des nombres ont été observés à la fin de la maternelle chez les enfants ayant participé au volet parental, comparativement aux enfants ayant bénéficié du programme en classe et dont les parents ne se sont jamais présentés aux ateliers auxquels ils s’étaient pourtant inscrits (groupe consentement-comparaison, CC).

D’après les commentaires de Rappaport (1977) à propos des recherches sur le programme Head Start, il y a une importante limite à n’établir à titre de groupe de comparaison que des enfants dont les parents ne se sont pas portés volontaires pour participer au programme. Ainsi, l’introduction d’un deuxième groupe de comparaison – composé d’enfants dont les parents se sont portés volontaires sans se présenter aux ateliers qui leur étaient destinés (CC) – procure une force supplémentaire à notre devis de recherche. Tous les enfants des deux groupes de comparaison (RS et CC) ont donc participé au programme d’éveil numérique en classe sans bénéficier de la participation parentale au programme. Toutefois, le groupe consentement-comparaison permet de distinguer parmi les enfants de ces deux groupes ceux dont les parents se montraient intéressés à la composante parentale du programme de ceux dont les parents n’ont pas manifesté d’intérêt. Autrement dit, sans cette variable, l’interprétation des résultats pourrait complètement errer puisque la différence entre ces groupes d’enfants quant aux résultats nous aurait échappée.

Les caractéristiques particulières des trois groupes à l’étude permettent de constater que les enfants du groupe consentement-comparaison se distinguent du reste de l’échantillon. De fait, ce groupe représente les familles dont le SSE se trouve le moins élevé ; on peut en déduire que les parents qui le composent nourrissent le taux le plus élevé de préoccupations quotidiennes et disposent, par conséquent, d’un minimum de ressources physiques et psychologiques pour éduquer leurs enfants. En plus de leurs nombreux soucis familiaux, de tels parents éprouvent généralement de la difficulté à collaborer à titre de partenaires avec le système scolaire (Aronson, 1996 ; Doherty, 1997 ; Moles, 1993), le plus souvent en raison de leur propre histoire académique souvent marquée par l’échec ou la frustration (Chavkin et Williams, 1989). Aussi sont-ils habituellement portés à laisser toutes les responsabilités de l’instruction aux autorités professionnelles (Graue, 1992 ; Lareau, 1989). De tels facteurs pourraient expliquer que les parents du groupe consentement-comparaison aient manifesté un intérêt à l’égard des ateliers proposés sans s’y présenter par la suite. Nous pouvons alors soumettre l’idée que les enfants des familles les moins fortunées précisément ciblés par le programme n’ont pas bénéficié de sa composante parentale.

En plus d’être constitué des enfants des familles les moins bien nanties, le groupe consentement-comparaison comprenait le plus grand nombre d’allophones et une majorité de filles (62,7 %). Selon Hanson (1992), les parents ne semblent pas entretenir d’égales attentes à l’égard du rendement en mathématiques de la part de leur garçon et de leur fille, préjugeant de meilleures performances masculines. Des analyses supplémentaires des résultats de notre échantillon n’indiquent pas de différence significative du rendement investigué entre les garçons et les filles ni au début, ni à la fin de la maternelle. Malgré l’absence de différence significative en mathématiques souvent observée entre les sexes à l’âge préscolaire et à l’école primaire (Jones, 1984 ; Friedman, 1989), certaines études rapportent que les parents sont réputés mieux soutenir le développement des habiletés numériques de leur fils (Entwisle et Alexander, 1990 ; Entwisle, Alexander et Olson, 1994) dans la foulée du stéréotype selon lequel les garçons démontrent un plus grand intérêt que les filles pour les différents champs des mathématiques. Par exemple, les parents sont davantage portés à fournir aux garçons des jouets et des jeux éducatifs susceptibles de stimuler le développement des habiletés préalables au succès en mathématiques (Hilton et Berglund, 1974) ; en revanche, ils encourageront plus volontiers chez les filles des activités relationnelles et des échanges verbaux, sans grand souci pour les concepts informels des mathématiques. Cette caractéristique socioculturelle pourrait expliquer, du moins partiellement, que les parents du groupe consentement-comparaison ne se soient pas présentés aux ateliers, croyant que le programme d’éveil numérique rencontrait moins les intérêts de leur fille.

Malgré les effets contraignants de la pauvreté, les parents de notre étude, tout comme ceux de l’étude de Galper, Wigfield et Seefeldt (1997), accordent de l’importance à la réussite scolaire de leur enfant. Généralement, cela représente un facteur susceptible d’influencer la participation des parents (Shriver, Kramer et Garnett, 1993) et, par ricochet, la performance de l’enfant. Contrairement à nos attentes, les parents dont les enfants ont démontré la plus piètre performance au Test de connaissance des nombres (Okamoto et Case, 1996) figuraient parmi ceux qui accordaient la plus grande importance aux résultats scolaires de leur enfant. Cette observation concerne davantage les deux groupes de comparaison, dont les sujets appartiennent aux familles de plus faible SSE, ont une mère moins scolarisée et des parents qui n’ont pas participé aux ateliers du volet parental. Dès lors, il est possible de penser que ces parents sont préoccupés par le fait que leurs enfants puissent traverser les mêmes difficultés qu’ils ont connues au cours de leur propre itinéraire scolaire ; ils accorderaient donc beaucoup d’importance aux résultats scolaires sans pour autant s’impliquer activement dans les activités que leur offre l’école (en l’occurrence, participer aux ateliers du volet parent). À ce sujet, Singh et ses collaborateurs (1995) avancent que les parents qui nourrissent de grandes attentes quant au succès scolaire de leur enfant ne lui offrent pas nécessairement un environnement familial plus stimulant et ne participent guère plus aux activités scolaires que les parents dont les attentes sont moins élevées.

Les ateliers-parents du programme Rightstart avaient pour but initial de sensibiliser les parents à un environnement familial qui stimule particulièrement l’apprentissage informel de la ligne numérique. Bon nombre de parents se sont prévalus de ces ateliers (42,9 % des parents sollicités ont participé à au moins un atelier), ce qui manifeste que les parents de faible SSE sont motivés et n’hésitent pas à s’engager dans des activités cognitives stimulantes lorsqu’ils sont sensibilisés à cet égard. Dans la mesure du possible, les ateliers-parents avaient été planifiés en fonction des disponibilités indiquées préalablement par les parents. De plus, tous les parents et les enseignants concernés recevaient un rappel téléphonique avant chaque rencontre et un agenda des rencontres ultérieures leur était fourni lors du premier atelier. Ces techniques de soutien ne sont pas sans avoir joué sur l’assiduité des parents aux ateliers. À ce sujet, Feuerstein (2000) rapporte que plus les parents sont sollicités, plus ils participent.

Les parents qui choisissent de participer à une intervention en milieu scolaire consacrent, pour la plupart, plus de temps à leur enfant et sont moins intimidés par l’école (Toomey, 1986). Indirectement, la participation des parents au programme Rightstart pourrait refléter un plus grand intérêt à l’égard de l’école et une plus grande participation dans l’éducation globale de leur enfant. Nous pouvons donc déduire que les enfants ayant bénéficié de la composante parentale du programme étaient probablement déjà plus stimulés par leurs parents à la maison et avaient par conséquent de meilleures chances de réussite scolaire. Ce facteur favorable pourrait ne pas apparaître dans les effets du traitement. Une telle difficulté en termes de précision statistique touche la plupart des études qui appliquent l’analyse de régression, ce qui incite à la prudence quant à l’interprétation des résultats d’une telle étude. En effet, les résultats sont discutés dans le contexte des variables préalablement établies à titre de variables prédictives. Bref, des facteurs non mesurés et corrélés avec la participation des parents ont pu influencer le rendement des enfants.

Suivant la littérature en ce qui a trait à l’analyse des résultats, les chercheurs relèvent surtout l’association entre deux variables, telle que la participation à un programme et les résultats qui s’ensuivent. Toutefois, il n’est pas sans intérêt de pousser plus loin afin de vérifier si cette association revêt quelque valeur pratique (McCartney et Rosenthal, 2000). Ainsi, le fait de rapporter un résultat significatif ou non significatif devrait s’accompagner d’une précision quant à son ampleur, afin de mesurer, en l’occurrence, la pertinence de l’intervention.

Dans notre étude, l’ampleur de l’effet observée indique une faible influence sur la connaissance des nombres chez les enfants terminant la maternelle. Comme en témoignent éloquemment les résultats du programme Perry Preschool, un effet, si faible soit-il dans une population vulnérable, peut éventuellement faire « boule de neige » et produire de surprenants résultats à long terme. Les enfants qui ont bénéficié de ce programme ont surpassé dans des proportions significatives les enfants du groupe contrôle sur plusieurs évaluations intellectuelles au terme de l’intervention et ce, jusqu’à l’âge de sept ans. Les effets ont toutefois disparu entre 7 ans et 14 ans (Hohmann et Weikart, 2002), bien que l’impact du programme se soit accru à l’âge adulte (Schweinhart, 2003).

Ces résultats sont certes très encourageants, mais la recherche a constamment démontré que les programmes préventifs appliqués au préscolaire en milieu socioéconomiquement faible entraînent des progrès à court terme aux plans cognitif et scolaire, quitte à disparaître avec les années (Reynolds, 1992). Cela peut s’expliquer par la piètre qualité des environnements scolaire (Brooks-Gunn, 2003 ; Currie et Thomas, 2000) et familial qui survivent à l’intervention. Cette limite est relevée dans plusieurs études de Head Start (Hubbell, 1983), dans le Consortium of Longitudinal Studies (Lazar, Darlington, Murray et Snipper, 1982) et tout particulièrement dans le programme High/Scope Perry Preschool (Schweinhart et Weikart, 1980). En revanche, la participation des parents ainsi qu’un soutien continu à la suite de l’intervention semblent constituer des mécanismes qui permettent le maintien de son efficacité (Bronfenbrenner, 1974 ; Dishion et Andrews, 1995 ; Zigler et Styfco, 1996).

Proposer des activités de participation parentale au cours des années préscolaires peut mettre en place une base solide au partenariat famille-école et favoriser une transition harmonieuse vers la première année. Les commentaires des parents, appelés à évaluer leur expérience lors de la dernière rencontre des ateliers, expriment majoritairement le caractère positif et enrichissant de ceux-ci. Il n’est donc pas utopique de croire que, appuyés sur cette expérience réussie de collaboration avec l’école, ils continueront à s’impliquer dans l’éducation scolaire de leur enfant, qu’ils porteront une plus grande attention à ses performances scolaires et qu’ils interviendront plus efficacement dans ce domaine (Olmsted, 1991 ; Seitz, Rosenbaum et Apfel, 1985).

Conclusion

Bien que la présente étude ne visait pas précisément l’évaluation de la mise en oeuvre du volet parental du programme Rightstart, il n’est pas sans intérêt de considérer l’application de certaines stratégies susceptibles d’avoir favorisé l’application intégrale du volet parental, dont le cahier de bord rédigé par chacune des intervenantes. L’analyse qualitative des cahiers de bord démontre que les éléments de contenu du programme semblent avoir été, dans l’ensemble, conformes au plan initial et appliqués de la manière prévue.

Cette étude n’est pas sans limite. Sur le plan méthodologique, une contrainte importante concerne l’absence d’une répartition aléatoire des sujets du groupe expérimental et des deux groupes de comparaison. En prenant la décision ou non d’appliquer le programme Rightstart en classe et en acceptant ou non de participer au volet parental du programme, les enseignants et les parents se sont pour ainsi dire autosélectionnés pour composer, ipso facto, les trois groupes de l’étude. Les enseignants, les parents et les enfants étudiés se différenciaient ainsi d’emblée des autres qui ont refusé l’invitation. Tout porte à croire que les enseignants volontaires étaient conscients d’un retard chez leurs élèves au chapitre des précurseurs cognitifs numériques, ce qui réclamait une assistance supplémentaire. Les résultats ont également permis de constater que les enfants bénéficiaires du volet parental amorçaient l’année scolaire munis de meilleures connaissances numériques. De plus, les ateliers-parents n’étant offerts qu’en français, la participation des familles allophones au volet parental s’est révélée très faible (28,3 %). Bref, les enfants ayant bénéficié du volet parental étaient probablement moins à risque que les enfants non participants (Hoover-Dempsey, Bassler et Brissie, 1992).

Bien que la proposition demeure insuffisamment démontrée à défaut de preuves empiriques (White, 1985 ; Ramey et Ramey, 1998), certains chercheurs (Bronfenbrenner, 1974 ; Garland, Swanson, Stone et Woodruff, 1981) ont constaté que plus les interventions ont lieu tôt dans le développement de l’enfant, meilleurs sont les effets. La période sensible pour l’apprentissage des notions de quantité relative se situe entre 48 et 60 mois (UNICEF, 2001). Or la majorité des sujets impliqués dans le programme d’éveil numérique Rightstart avaient outrepassé cette période : ils avaient en moyenne 67 mois.

Il serait intéressant de répéter notre expérience auprès des enfants de quatre ans pour lesquels une nouvelle version inspirée du programme Rightstart a été mise au point (le programme Bon Départ), quitte à adapter le volet parental. Selon Pagani et ses collaborateurs (2006), le programme Bon Départ implanté en prématernelle a produit de meilleurs effets à court terme en ce qui a trait à la connaissance des nombres chez les enfants de milieu socioéconomiquement faible que le programme Rightstart appliqué à la maternelle. La collaboration des parents à une telle intervention constituerait un important facteur additionnel pour augmenter les chances des enfants de milieu socioéconomiquement faible d’aborder leur curriculum académique dans de bonnes conditions d’ordre cognitif.