La dualité de Lautman contre la négativité de Hegel, et le paradoxe de leurs formalisations : contribution à une enquête sur les formalisations de la dialectique

Barot, Emmanuel

doi:https://doi.org/10.7202/039715ar

Introduction : deux motifs

Cette étude s’insère dans une enquête large et au long terme portant sur les rapports entre science, philosophie et idéologie, rapports gros d’enjeux politiques puisque s’y ordonnent nécessairement l’organisation du lien socio-politique entre savoir et pouvoir, et corrélativement l’évaluation des formes de discursivité et des scientificités légitimes[1] : le noeud gordien, ou le fil rouge de l’enquête, c’est la dialectique, dont les xix^e et xx^e siècles ont montré, autant en matière épistémique que politique, en particulier par le marxisme, la centralité. Un des points de départ de l’enquête, c’est bien sûr Hegel. Or notre propos, ici, porte sur la pensée de Lautman : un certain nombre de facteurs nous ont motivé à confronter les deux, facteurs que le présent article souhaite exposer. Et il faut en tout premier lieu reconnaître qu’au premier abord, si ce n’est pas la présence du terme « dialectique », il pourrait sembler saugrenu de rapprocher Lautman de Hegel dans la mesure où le premier ne cite, dans toute son oeuvre, jamais le second.

Indépendamment des causes qui ont fait de Hegel, de façon générale, l’impensé épistémologique des philosophies et épistémologies « continentales » du xx^e siècle, qui expliqueraient certainement cette absence de mention, on doit noter que, malgré tout, certains commentateurs ont pourtant fait, à forte raison, le rapprochement : J. Petitot dans son article de 1987 « “Refaire le Timée”. Introduction à la philosophie mathématique d’Albert Lautman », et J.-M. Salanskis en 1991 dans L’herméneutique formelle[2] de 1991. Or l’un comme l’autre, héritiers de l’anti-dialectisme offensif de Deleuze, semblent d’une part vouloir dire que cette proximité avec Hegel n’est forcément pas la meilleure chose à souhaiter à Lautman, ou du moins n’est pas ce qu’il y a de plus convaincant dans son dispositif. D’autre part, s’il faut ici vivement les remercier d’avoir initié la confrontation, ils ne pointent qu’incomplètement le lieu, les enjeux et les limites de cette dernière. Nous proposons ici en première partie de reprendre cette enquête qu’ils ont initiée il y a une vingtaine d’années[3].

On revient d’abord sur le problème qui est fondamental à la fois pour Platon et Lautman, celui de la « détermination » de l’indéterminé, problème converse de celui de la « participation ». On montre ensuite que la façon dont Lautman le résout le rapproche à deux titres de Hegel : en substituant concrètement à l’idée de participation le modèle d’une « actualisation » dialectique de l’Idée par la médiation de son Autre, et en développant une « antithétique » (termes de J.-M. Salanskis et J. Petitot) de l’Idée affine à la dialectique de la contradiction interne chez Hegel. Enfin, en enchâssant trois divergences de fond entre les deux, on met en évidence ce qui les sépare fondamentalement, et qui n’est autre qu’une divergence de fond entre Hegel et Platon dont Lautman se réapproprie la thèse essentielle : leurs conceptions respectives du rapport primitif qu’entretiennent le Même et l’Autre, l’Un et le multiple, c’est-à-dire l’origine de la dualité.
En seconde partie[4], partant d’un tout autre bout du problème, nous motivons a posteriori, cette fois par les effets, le rapprochement Lautman-Hegel, en montrant comment leur divergence philosophico-métaphysique sur cette origine de la dualité trouve une traduction explicite et précise dans les entreprises ou projets de formalisation de leurs dialectiques respectives. On s’appesantit, à cette fin, essentiellement sur la belle tentative de 1972 de A. Doz et D. Dubarle dans Logique et dialectique, et d’autre part sur la suggestion-projet de F. Zalamea[5] de 2006, de traduire la dialectique des Idées et schémas de structures lautmaniens dans l’idiome de la théorie des catégories.

L’enjeu de l’étude que nous esquissons ici est le suivant : il y a des rapprochements conceptuels importants entre Hegel et Lautman, mais une divergence fondamentale au sujet de la contradiction et de la négativité, qui est au coeur de la question de la dialectique. Or, on va le voir, les formalisations qu’on peut respectivement esquisser de leurs dialectiques semblent pouvoir être traductibles l’une dans l’autre. D’où un problème clé : est-ce que cela indique que leurs dialectiques sont en réalité de même nature, ou est-ce que cela indique que l’opération de formalisation échoue à saisir leur divergence conceptuelle, et derrière celle-ci, la négativité proprement dite ? Le but est par là d’interroger la vertu, la pertinence de cette entreprise de formalisation, et d’en identifier les points critiques.

I. Pertinence et limite du rapprochement des doctrines de Lautman et Hegel

1. Le problème de la détermination : participation et composition

Dans le dialogue platonicien qui porte son nom, Parménide met progressivement en évidence une série d’apories touchant les rapports de l’Un et du Multiple : le fond du problème étant de saisir les principes unificateurs nécessaires de la diversité des choses sensibles contingentes. Ces apories sont groupées en huit « hypothèses » questionnant et évaluant les types de rapports possibles entre Un et Multiple, et portent tout particulièrement sur les grands couples de « contraires »[6] qui semblent affecter ou devoir caractériser les Idées pour qu’elles jouent de façon cohérente leur rôle de principe ontologique (être au principe de l’existence et du mode d’existence des choses sensibles) et épistémique (être au principe de la connaissance de ces derniers). Une première difficulté, c’est que ces couples de contraires sont parfois des contraires logiques, c’est-à-dire des couples dont l’un des membres est la négation de l’autre (au sens de ce qui se rapproche de la « contradiction » selon la bivalence standard, comme Divisible /Indivisible ou encore Fini/Infini en nombre), parfois des contraires non logiques (ainsi « En elles-mêmes/relativement », ou « Grandes/Petites », ou, chez Lautman, « Structure-existence »), c’est-à-dire que la relation de contrariété existant entre les deux membres ne se résout, au mieux, qu’en une « opposition » en un sens très large, mais parfois seulement en une distinction de points de vue. Les difficultés traditionnellement attachées à cette non-systématicité, cette variation, cette relative indétermination de la relation de contrariété, se retrouvent telles quelles chez Lautman.

Le jeune Socrate propose comme solution matricielle à ces apories la thèse de la « différence ontologique » entre Formes séparées, intelligibles, Idées nécessaires et non soumises au devenir, et ces choses ou phénomènes sensibles, dont il dit qu’ils tirent leur consistance, leur type d’être de leur « participation » à ces Idées[7]. Cette « participation » est d’abord proche de la notion pythagoricienne de « mimésis » ou ressemblance[8] : une chose est ce qu’elle est en vertu de sa ressemblance avec ce qui constitue pour elle un modèle, l’Idée. Mais cette notion de participation semble imposer que l’Idée se « pluralise » dans les choses : le risque de sa dissolution est alors proche. Autrement dit, la thèse de la participation est fort problématique parce que derrière elle sont en jeu l’unité et l’identité de la forme séparée qu’est l’Idée. D’un autre point de vue, un élément central chez Platon, c’est l’idée selon laquelle chaque chose sensible est un « mixte », c’est-à-dire le résultat d’un processus de composition d’éléments ou principes distincts. Toute chose est un composé, c’est-à-dire le résultat de l’action de la peiras (« limite ») sur l’apeiron (« l’illimité »)[9], c’est-à-dire une opération donnant une « détermination », c’est-à-dire forme et proportion[10], donc existence spatio-temporelle particulière, à quelque chose qui est « indéterminé », un principe fluent qui sera, dans le Timée, la « cause errante » ou khôra.

Le lien entre la composition et la participation n’est pas simple à établir, puisqu’il faut établir le lien entre Idées et limite-illimité, mais de façon transversale, et sans entrer dans les détails spécialisés de l’interrogation on peut dire que la question de la mixité-composition est l’autre nom de la participation : les deux problèmes sont converses.

Il est possible de se demander dans quelle mesure une forme détermine l’existence et les propriétés de la matière à laquelle elle est susceptible de s’appliquer. C’est là un problème philosophique capital pour toute théorie des idées, puisqu’il ne suffit pas de poser la dualité du sensible et de l’intelligible ; il faut encore expliquer la participation, c’est-à-dire, de quelque nom qu’on l’appelle, la déduction, la composition ou la genèse du sensible à partir de l’intelligible[11].

C’est dans les termes d’un tel procès de détermination-de-ce-qui-est-indéterminé que Lautman pose le problème du rapport entre Idées (dialectiques) et théories (mathématiques). Le coeur du dispositif, ce sera l’interprétation des modalités effectives de ce procès, interprétation qui justement le rapproche de Hegel.

2. De l’indétermination à la « définition-résolution »

La pensée de Lautman est explicitement dominée par une antithétique : le rapport Idées-Théories est chez lui fondé sur un principe de développement, de croissance, et de réalisation historique mobilisant les Idées qui sont entendues comme dualités, comme couples notionnels[12].

[N]ous appellerons Idée le problème de la détermination de liaison à opérer entre notions distinctes d’une dialectique idéale[13].

Chez Lautman, l’Idée comme couple de notions renvoie au problème de la détermination : le problème est celui du type de liaison entre deux « notions » faisant couple, c’est-à-dire de la nature de la relation de contrariété qui les associe. Autrement dit, le problème, c’est celui de l’indétermination première de cette relation. Or, dans ce genre de citations, emblématique de toute les définitions de l’Idée qui jalonnent l’oeuvre de Lautman, les commentateurs ont beaucoup insisté sur la notion de « problème », Deleuze le premier dans Différence et répétition, mais, à nos yeux, franchement pas suffisamment sur « détermination ».

La grande thèse de Lautman est la suivante : il existe donc une indétermination foncière au coeur de l’Idée, puisque c’est une indétermination de la relation unissant les couples de notions par lesquelles il définit l’Idée. Or l’opération de détermination de cette indétermination ontologico-métaphysique est pour lui totalement l’affaire des mathématiques au coeur de leur histoire : c’est cela le sens de son affirmation selon laquelle les théories sont une « réponse » au dit « problème ». Ces Idées-couples, relativement indéterminées, sont ainsi d’abord caractérisées par une « insuffisance essentielle », une « virtualité » (Deleuze), c’est-à-dire par une ouverture vers une pluralité de « liaisons possibles » déterminées entre notions. Autrement dit les Idées ont « besoin » de la « matière mathématique » pour prendre corps, c’est-à-dire pour subir leur détermination.

Seulement, et c’est là que les choses deviennent complexes, la nature de ce processus de « réponse » ne va pas de soi. Avant d’en dire plus, on peut déjà rappeler que c’est cette perspective particulière qui impose à Lautman la double méthode non historiciste — si l’épistémologie historique de ses homologues dialectisants français, comme Cavaillès ou Bachelard, et surtout son maître Brunschvicg est une condition nécessaire, elle n’est à aucun titre suffisante — qu’il explicite dans ses Nouvelles recherches sur la structure dialectique des mathématiques de 1939. La double méthode consiste soit à partir de l’Idée pour voir comment la théorie lui donne singulièrement corps, soit à partir de la théorie singulière pour voir comment son organisation et sa conceptualité renvoient à l’Idée.

Dans cette double méthode, d’un côté l’on va de l’Abstrait (Cause) au Concret (Effet), de l’Idée aux théories, selon un développement analytique homologue au passage de l’Un au Multiple par division (diérèse), alors que de l’autre côté, on va justement du Concret (Effet) à l’Abstrait (Cause), des théories à l’Idée, selon un mode synthétique de rattachement, de rassemblement du Multiple en l’Un[14]. On a ici évidemment affaire à une formule de la dialectique doublement ascendante et descendante. Mais contre Platon et Heidegger, on assiste à une subversion, une annulation substantielle de la « différence ontologique » : le rapport ontologique entre Idées-Causes et Théories-Effets n’est évidemment plus celui de la causalité éponymique, mais celui — c’est notre thèse — d’une actualisation dialectique.

3. L’actualisation dialectique

En quel sens faut-il parler « d’actualisation dialectique » ici ? Non pas au sens où une théorie actualiserait, ferait passer de la « puissance » à « l’acte » un principe supérieur déjà organisé, pré-établi, ce qui correspondrait à une lecture platonicienne standard (et légitime). Mais au sens où une théorie « répond » à l’Idée-problème en la définissant et la résolvant à la fois, c’est-à-dire, justement, en la déterminant. Reprenons une citation fondamentale de Lautman :

La philosophie mathématique, telle que nous la concevons, ne consiste donc pas tant à retrouver un problème logique de la métaphysique classique au sein d’une théorie mathématique qu’à appréhender globalement la structure de cette théorie pour dégager le problème logique qui se trouve à la fois défini et résolu par l’existence même de cette théorie[15].

L’indéfinition logiquement antérieure du « problème logique », c’est-à-dire de l’Idée, montre à quel point l’Idée est suspendue aux théories pour trouver sa propre consistance : autrement dit, l’Idée n’est pas un simple principe transcendant les théories, qui n’en serait qu’une « réalisation concrète », une « copie », etc. La conséquence, aussi anti-platonicienne qu’anti-socratique, c’est l’impossibilité radicale de toute connaissance directe de l’Idée, c’est-à-dire l’impossibilité d’une connaissance contemplative de l’Idée, ce que pourtant la République présentait comme le but et la consécration de la méthode dialectique. En effet :

La réalité inhérente aux théories mathématiques leur vient de ce qu’elles participent à une réalité idéale qui est dominatrice par rapport à la mathématique, mais qui n’est connaissable qu’à travers elle. Ces Idées sont donc bien distinctes des purs arrangements de signes, mais elles n’en ont pas moins besoin d’eux comme d’une matière mathématique qui leur prête un corps où puisse s’affirmer le dessin de leurs liaisons[16].

On ne peut connaître l’Idée qu’à travers les théories, et cela, tout simplement parce que l’Idée ne peut devenir « objet » déterminé de pensée et de discours qu’à travers ces dernières : les théories sont la « réponse » à un « problème » qu’elles sont seules à instituer comme problème. On peut donc maintenant questionner plus avant l’idée d’« actualisation dialectique », au regard de cette définition-résolution mathématique des Idées. La première traduction, c’est que les Idées ne sont pas mathématiquement déterminantes, c’est-à-dire ne sauraient préfigurer, pré-formater, pré-déterminer par avance les contenus (les structures, les objets, les méthodes, etc.) des théories, qui ressortent dès lors autonomes dans leur développement historique concret par rapport à ces Idées. C’est pour cela que J. Petitot qualifie les Idées de « réfléchissantes » au sens kantien, lecture dans le sillage de Deleuze qui insistait sur le fait que, descriptivement, le terme de « problème » fait référence à Kant et aux Idées de la raison qui ne sont pas constitutives d’objets.

Cependant, comme pour Socrate, on voit tout aussi bien ici que les théories mathématiques n’épuisent pas les « problèmes » auxquels elle donnent une solution déterminée : les Idées sont « distinctes » des théories, même si elles ont « besoin » d’elles pour que « s’affirme le dessin de leurs liaisons », c’est-à-dire pour que s’incarne singulièrement ce dont elles sont « grosses ».

4. Trois degrés possibles d’indétermination de l’Idée

Autrement dit, ces problèmes ne sont que partiellement indéterminés. On peut ici établir une gradation entre trois visages ou trois « natures » possibles du « problème », c’est-à-dire trois conceptions possibles du degré d’indétermination qui le caractérise. Or de l’option interprétative retenue — sachant que deux des trois seulement sont en réalité raisonnables — va découler une lecture distincte de Lautman.

La première option n’en est pas vraiment une ici, au sens où elle est absolument étrangère à Lautman. On peut imaginer que le « problème » est en fait simplement une « question » précise, appelant une réponse précise au sens réduit du terme. Ici, on serait en face de la détermination maximale au plan métaphysique de l’Idée, le problème étant alors pleinement « positif », scientifiquement « déterminé » et sensé : cela pourrait correspondre à une évacuation positiviste du plan métaphysique.
En revanche, le problème comme « problème » ne peut, lui, appeler qu’une « solution ». Littéralement parlant, c’est la perspective de Lautman : il y a déjà une certaine organisation de l’Idée-problème au plan métaphysique, c’est-à-dire une détermination relative, puisqu’elle a la forme d’un couple de notions. Détermination relative de l’Idée, qui est fort logiquement, et rigoureusement, proportionnée à son « indétermination ». Ici, la dialectique de Lautman est bien une « Problématique », comme cela a été rappelé par divers commentateurs.
En revanche, une troisième lecture du « problème » a été proposée, celle de J.-M. Salanskis : il ne lit le problème ni comme une question ni comme justement un problème, mais comme une « énigme », appelant cette fois une « compréhension ». Existerait ainsi une « pré-compréhension » par les théories d’une énigme essentiellement, majoritairement indéterminée. Cette lecture est conforme à l’idiome de Heidegger, et le terme est effectivement utilisé par Lautman en 1939 dans ses Nouvelles recherches. D’où la thèse selon laquelle la « problématique » lautmanienne est ou convoque non pas une dialectique, mais une « herméneutique ».

Ainsi, la lecture choisie de l’opération de « définition-résolution » se cristallise sur la lecture de ce qu’est un « problème » logique (c’est-à-dire dialectique), et le partage entre le « problème » (favorisé par la référence à Platon, et à tonalité hégélienne) et l’« énigme » (favorisé par la référence à Heidegger) a un impact majeur important. La problématique/dialectique ouvre à une antithétique de notions duales, alors que la lecture herméneutique récuse cette antithétique. Et c’est bien cela que J. Petitot et J.-M. Salanskis défendent, suivant Deleuze et reconduisant son anti-hégélianisme massif : même s’il est « incomplet » le « problème » est déjà trop déterminé par soi sous la forme de la dualité, et donc trop proche de Hegel. Plus précisément, les deux affirment que Lautman est bien effectivement proche de Hegel, mais s’en détachent alors justement pour cela et accentuent leur lecture explicitement néo-kantienne (comme toute l’épistémologie française-allemande, néo-kantienne et post-hégélienne l’avait d’ailleurs fait), sous deux déclinaisons proches : heideggerienne chez J.-M. Salanskis, husserlienne chez Petitot (cette fois du fait de la référence de Lautman à « l’eidétique descriptive » lors de la séance de la Société française de philosophie de 1939[17]).

L’essentiel à retenir maintenant, c’est donc que J. Petitot et J.-M. Salanskis ont raison de rapprocher en partie Lautman de Hegel, bien qu’ils n’établissent d’une part qu’incomplètement les raisons de leur proximité, et donc les motifs du rapprochement, et bien que d’autre part, il n’exhibent, là encore qu’incomplètement, ce qui les sépare fondamentalement. Récapitulons ce qui a été établi :

Les Idées ne sont connaissables qu’à travers les théories qui les accomplissent. Ce qui est anti-platonicien : cela signifie qu’il n’y a pas de connaissance proprement contemplative, mais seulement connaissance régressive et indirecte de l’Idée sur le fond du procès d’actualisation.
Conséquence : les Idées, définies et résolues par les théories, leur sont donc à la fois transcendantes et immanentes :

En tant que problèmes posés, relatifs aux liaisons que sont susceptibles de soutenir entre elles certaines notions dialectiques, les Idées de cette dialectique sont certainement transcendantes (au sens habituel) par rapport aux mathématiques. Par contre, comme tout effort pour apporter une réponse au problème de cette liaison est, par la nature même des choses, constitution de théories mathématiques effectives, il est justifié d’interpréter la structure d’ensemble en termes d’immanence pour le schéma logique de la solution cherchée. Il existe donc un lien intime entre la transcendance des Idées et l’immanence de la structure logique de la solution d’un problème dialectique au sein des mathématiques ; ce lien, c’est la notion de genèse qui nous le donne[18].

Là encore, on va à l’encontre de Platon et de Heidegger : la différence ontologique est quasiment annulée. Or du fait que les Idées sont des schémas des liaisons spécifiques possibles établies entre notions contraires formant couple, et que la dynamique de leur réalisation passe par le jeu de cette dualité, la dialectique de Lautman est clairement une antithétique, ce qui est pleinement hégélien : ce qui faisait donc dire à J.-M Salanskis que « le Platon de Lautman est aussi un Hegel »[19].
Les Idées ne sont pas de simples « apparences » ou des produits de la Raison, ni simples esquisses ni « concepts réflexifs », puisqu’elles sont « transcendantes » au sens « habituel » (platonicien) du terme. Pourtant, la circularité qui les affecte est clairement anti-platonicienne : cette circularité est formulée par J.-M. Salanskis[20] dans les termes d’un cercle herméneutique.

Sur les lectures de G. Deleuze et de J.-M. Salanskis et sur le cercle herméneutique

Une parenthèse s’impose ici, avant de revenir directement sur le rapport Lautman-Hegel. J.-M. Salanskis écrivait en 1998 que « la lecture de Deleuze m’a incité à lire Lautman, ce dont je ne lui serai jamais assez reconnaissant[21] ». Il faut donc dire quelques mots sur cette intervention deleuzienne, concentrée dans son livre de 1968, Différence et répétition. Contre le privilège traditionnellement accordé au même et à l’unité, privilège appauvrissant l’appréhension du réel, Deleuze met en avant de façon transversale la différence, dans l’ordre des idées comme celui des phénomènes sensibles, et sans être aucunement le retour du même, la répétition est en réalité celle du singulier. Son orientation est concrètement la suivante : montrer que la « différence » n’exprime pas la contradiction, de même que la « répétition » n’exprime pas l’identité. L’anti-hégélianisme massif qui est le sien, rappelé dès l’Avant-propos[22], l’amène à penser une différence qui soit pure divergence, et une répétition qui, derrière ses déguisements, s’enracine dans une « raison cachée » qui n’est autre qu’un différentiel à l’oeuvre. L’étude du sens du rapport différentiel , qui est pour lui l’objet d’une « Idée »[23], concentre bien d’ailleurs cette posture : cette étude est gouvernée par la prédominance de la variabilité mutuelle des termes du rapport sur la multiplicité quantitative qu’ils sont censé indiquer, et Deleuze la développe sans référence aucune à la longue « Remarque sur l’infini mathématique » que Hegel consacre dans la Science de la logique à cette question, bien que la lecture effectuée du problème soit sensiblement comparable. C’est en tous cas dans la foulée de cette analyse que Deleuze en vient à « l’oeuvre admirable »[24] de Lautman, dont il reprend la thèse transversale selon laquelle « un problème n’existe pas hors de ses solutions », mais « insiste et persiste dans ces solutions qui le recouvrent »[25]. Citant Canguilhem et Bouligand[26], il martèle qu’un problème est irréductible à telle solution qu’on peut lui trouver. Deleuze avait auparavant patronné la discussion de ces Idées-problèmes par la référence kantienne : Kant ne cessait de dire que les Idées étaient « problématiques » ou « problématisantes » au sens de « problèmes sans solution » exprimant une dimension de l’objectivité elle-même, dès lors qu’elle traite d’un au-delà de l’intuition sensible. Ces Idées sont, de là, des « foyers », des horizons totalisants : la raison certes produit de faux problèmes, puisqu’ils reposent sur un usage illégitimement déterminant de l’Idée, mais, dit Deleuze, ces problèmes ne sont pas nécessairement faux : c’est même la faculté de la raison que de se poser ce genre de « faux problèmes »[27].

De ce fait, toute Idée est un problème, et « dialectique » au sens kantien. Dès lors, si l’on omet que le problème est Idée en ce sens, on tombe dans l’illusion hégélienne de sa puissance déterminante, c’est-à-dire dans l’illusion qui fait tomber la dialectique dans la négativité et qui achève la dénaturation de cette « problématicité » irréductible de l’Idée. La difficulté est que Deleuze crédite Lautman de cette lecture sans rappeler à quel point la position de ce dernier n’est pas limpide. L’exemple qu’il prend ensuite conforte à juste titre sa lecture : penser ce mouvement de production de la différence l’amène à tenter de rendre raison du virtuel et du procès d’actualisation. Le slogan lautmanien selon lequel les Idées ou multiplicités — assimilées à la partie « virtuelle » à l’oeuvre dans le processus d’individuation — sont des « problèmes » dont les êtres individuels sont les solutions, gouverne alors sa reprise de la discussion par Lautman du rôle des singularités d’un système d’équations différentielles[28] (points singuliers requis pour la détermination d’une courbe) pour montrer, arguant du fait que ces singularités et surtout le mode de leur structuration fournissent le cadre des solutions possibles, que l’Idée est jeu, dans le virtuel, de la différence avec soi, jeu à partir duquel s’engendrent les choses individuelles.

Deleuze s’inscrit ici, comme il le fera dans ses travaux sur Nietzsche, dans le champ de la discussion des grandes figures post-kantiennes de la philosophie allemande, auxquelles on ajoutera évidemment Spinoza, mais surtout sans Hegel. Pourtant, cette nature partiellement prescriptive de l’Idée, dont on vient de voir à quel point elle est difficile à proportionner, pourrait sans problème être reformulée « à la Hegel » : l’Idée (le problème) s’auto-prescrit la forme de sa propre résolution, c’est-à-dire se réalise (s’accomplit en dépassant son indétermination) par un auto-développement qui est contradictoire, puisque c’est par la médiation de son autre qu’elle pose comme tel en l’exigeant (le système structuré de singularités). Mais Lautman ne le dit pas ainsi — et ce serait de toutes façons forcer le trait — et Deleuze encore moins. Il n’empêche, là encore la situation est singulièrement instructive : comme le résume J.-M. Salanskis, dans ce chapitre de Différence et répétition, Deleuze « fait du » Hegel sans le dire[29].

Revenons maintenant au cercle herméneutique. Selon J.-M. Salanskis, on ne cherche à résoudre que ce qui pose question[30], ce qui « insiste » sans exister comme tel, et la résolution fait exister formellement ce qui ne faisait qu’insister comme sens possible — ce qui insiste n’existe pas. La circularité ici ne peut être platonicienne : herméneutique, elle signifie que des problèmes « insistent » dans l’universel-indéterminé et que les théories les font exister dans une particularité déterminée : cette antériorité logique du « souci », de la question sur la réponse, alliée à la priorité gnoséologique de la réponse effective trouve sa formulation canonique au § 63 d’Être et temps (1927). Objet d’une pré-compréhension sous-jacente, d’une « familiarité » qui est en même temps un « écart » ou « désaisissement », l’énigme pré-mathématique, proto-mathématique, voire extra-mathématique (ce n’est pas tranché) suscite la recherche mathématique qui en retour va affiner sa détermination. Et l’énigme majeure, pour J.-M. Salanskis, c’est l’excès « intuitif » que véhicule l’espace, dans ses attributs infinitaires et continus non réductibles à la captation logico-mathématique[31].

Malgré tout, rien n’empêche avec les textes de Lautman de dire que, si cercle herméneutique chez Lautman il y a, c’est fort possiblement comme avatar conceptuel du cercle dialectique hégélien[32]. Et cela d’autant plus que l’Idée-problème est concrètement difficilement assimilable à l’énigme, d’où une autre difficulté dans la lecture qu’en proposait J.-M. Salanskis dans L’herméneutique formelle, liée à une autre distinction, celle entre les discours de type « destinal » (ou post-heideggerien) et de type « généalogique ». Le destinal renvoie au motif herméneutique de l’appréhension circulaire d’une énigme indéterminée, le généalogique à celui d’une remontée des théories aux Idées qui serait la remontée vers son proto-contenu objectif et déterminant. Or, pour Lautman, il n’y a rien de tel dans les Idées. Le discours lautmanien, s’il n’est pas « destinal »-herméneutique au sens d’une réponse à une énigme initialement pré-comprise, n’est pas non « généalogique » en ce second sens, puisqu’il ne propose en rien un discours de l’actualisation d’un pré-donné.

Il y a de surcroît une non-fixité, un devenir dialectique des Idées, celles-ci étant constituées et hiérarchisées au sein d’un procès de constitution qui ne renvoie pas à un autre procédé plus primordial auquel il faudrait régresser : ce qui est en propre, outre cette limite objective à la régression, la thèse d’une pluralisation des déterminations de l’Idée.

La métamathématique qui s’incarne dans la génération des Idées et des nombres ne saurait donner lieu à son tour à une métamathématique ; la régression s’arrête dès que l’esprit a dégagé les schémas selon lesquels se constitue la dialectique[33].

Ces quatre points sonnent de façon bien hégélienne. Donc c’est bien de Hegel que Lautman semble se rapprocher le plus. Mais en travaillant ce rapprochement on voit que l’affinité ne tient que jusqu’à un certain point seulement, insuffisamment mis en relief par ceux-là mêmes qui éloignent Lautman de Hegel. Nous allons donc leur donner raison, mais en exhibant l’argument qui leur manque.

5. Le fondement du procès logique selon Hegel, et sa différence d’avec Lautman

Dire que Lautman est proche de Hegel n’a rien d’étonnant : Hegel a tout de même forgé sa position au travers d’une lecture étroite de Platon, et il rappelle très clairement leurs affinités dans ses Leçons sur Platon de 1825-1826. Voyons donc dans le détail jusqu’où Lautman est au moins aussi hégélien que platonicien. Chez Lautman et Hegel est défendue une dialectique de l’Idée, c’est-à-dire de l’Universel, qui ne se concrétise dans toutes ses potentialités que par son passage dans le multiple : comme Universel qui s’actualise, il est détermination de soi par passage dans le multiple, et, réciproquement, le multiple trouve sa cohésion et son ordre parce qu’il est sous la gouverne de cet Universel. Corrélativement, dans les deux cas, le spéculatif-dialectique est le plan de ressaisie dans leur nécessité onto-logique des savoirs théoriques positifs légués par l’histoire des sciences, partiellement aveugles à leurs fondements : cette nécessité, chez les deux, est fondée sur une antithétique de notions contraires.

Pour Hegel, le vrai, c’est le tout dans le mouvement qui fait de lui un résultat, et l’Idée, c’est la totalité des déterminations qui s’accomplit comme totalité innervant cette diversité dans et par un procès multiforme, et avant tout, dans un procès logique dans la Science de la logique dont son Concept préliminaire[34] à L’Encyclopédie des sciences philosophiques donne une formule très claire. L’idée comme processus propre et nécessaire est engendrement et fondation en même temps que réappropriation d’un donné d’entendement singulier et de l’existant singulier que ce dernier représente en extériorité — c’est-à-dire exige pour soi la médiation de son autre, cette réalisation du plan du réel, afin de pouvoir prendre forme et poursuivre son développement. Chez Hegel, cette auto-diction du Concept joue bien la fonction d’une épistémologie au sens contemporain, mais en reprenant une ambition tout à fait traditionnelle : celle des métaphysiques classiques prétendant livrer, par leur instruments propres, les principes derniers de la connaissance humaine, par-delà les savoirs particuliers acquis dans les sciences. Ainsi, ce méta-discours spéculatif-dialectique est tout sauf seulement d’explicitation et de restitution : il est ontologie au sens où il dit la nature et les conditions d’advenue du réel des sciences (et des mathématiques).

Pourtant, pour Hegel, la science peut de fait se passer du philosophe, mais pas l’inverse. Ainsi disait-il déjà en 1803 que :

La raison sans l’entendement n’est rien, l’entendement sans la raison est pourtant quelque chose[35].

De la même façon, chez Lautman, les théories naissent et se développent par elles-mêmes, même si au niveau de la conceptualité propre qu’elles déploient, la domination métaphysique des Idées en constitue le principe d’intelligibilité. Or, on l’a rappelé au début, cette relation de « contrariété » elle-même est relativement indéterminée, ce qui rend possible justement ses multiples traductions : or c’est là le point essentiel sur lequel Lautman et Hegel vont véritablement diverger. En effet, trois éléments enchâssés les différencient, qui sont à reconduire à une même divergence de fond.

A. L’absence d’Aufhebung chez Lautman

Le premier élément, immédiatement visible à la lecture mais non auto-explicatif, c’est l’absence d’Aufhebung dans l’antithétique lautmanienne, alors que c’est un maître mot chez Hegel.

Dans la Science de la logique[36] Hegel rappelle que Kant part de l’idée que nous ne connaissons pas les choses en elles-mêmes mais comme Erschneinungen, comme phénomènes, c’est-à-dire phénoménalisation d’un système de rapports constitutifs du réel comme objet. L’impossibilité d’une connaissance au-delà de ces phénomènes l’amène, dans la « Dialectique transcendantale » de la Critique de la raison pure, à énoncer les quatre antinomies de la raison pure, c’est-à-dire quatre couples d’énoncés dont les concepts sont soit trop « grands » soit trop « petits » pour leur objet, incommensurabilité de la raison à son « objet » due à sa propre nature. Or si la raison ne peut en réalité connaître que des objets sensibles, donnés dans l’espace et le temps, c’est-à-dire des phénomènes, selon Kant rien ne peut supprimer ce mouvement d’illusion en sa racine : on peut en prendre conscience pour s’en préserver autant que possible, et la philosophie doit tenter de limiter et corriger les erreurs de la raison. Mais on ne peut les détruire sans détruire la raison elle-même. Le geste kantien aboutit ainsi, en tant que geste du point de vue du sujet (transcendantal), à montrer l’objectivité et la nécessité des antinomies[37] qui surgissent de la détermination particulière des catégories de la connaissance, donc la nécessité de la dialectique transcendantale. La finité de ses facultés et des instruments de sa connaissance impliquent pour Kant que ces antinomies mènent à l’impossibilité de produire un concept de l’absolu et de l’infini apte à dépasser au point de vue théorique ces antinomies, et donc, à l’impossibilité de connaître la « chose en soi ».

Au contraire, exposer les quatre antinomies en les dégageant de leurs applications concrètes permet à Hegel d’en trouver la solution véritable, qui

ne peut consister qu’en ce que deux déterminations, en tant qu’elles sont op-posées et nécessaires au même concept, ne peuvent valoir dans leur unilatéralité, chacune pour soi, mais en ce qu’elles n’ont leur vérité que de leur être-sursumé[38].

Les couples de notions opposées qui forment l’Idée sont bien nécessaires à sa détermination comme problème exigeant actualisation pour Lautman, de même que pour Hegel la dissociation unilatérale de chaque notion lui fait perdre le sens même de son effectivité. Mais l’« être-sursumé » qui à chaque étape nous rapproche de la complétude, c’est-à-dire le résultat de l’Aufhebung chez Hegel, le moment du dépassement de la contradiction existant entre deux déterminations notionnelles (comme Être et Néant, dont le dépassement à la fois annulant et intégrant leur opposition est le devenir), n’existe pas chez Lautman. Il n’y a pas chez ce dernier de synthèse supérieure accomplissant et dépassant la contradiction entre notions opposées : l’antithétique dialectique ne fonctionne pas selon le même mode chez les deux, c’est-à-dire que la réalisation de l’universel chez Lautman ne s’effectue pas par contradiction.

B. L’absence de contradiction et de négativité interne chez Lautman

Ce qui est sous-jacent à l’absence d’Aufhebung chez Lautman, c’est le fait que son antithétique n’en est pas une de la contradiction. Son antithétique de la « contrariété », l’extension du concept étant chez lui assez large, est bien plus proche des antithétiques de la « corrélation » caractéristiques des néo-kantiens post-hégéliens, dont Renouvier, Hamelin, jusqu’à Bachelard, sont d’illustres représentants. La seule originalité de Lautman ici, c’est que ce post-hégélianisme de la corrélation n’a pas sa source chez Kant, mais chez Platon même.

Revenons à Hegel : chez ce dernier, les différentes modalités du procès dialectique sont en dernière instance expressives de la modalité centrale qu’est la contradiction, et, de façon générale, de la négativité à l’oeuvre : le passage d’une détermination à sa détermination contradictoire s’opère grâce à la position en soi-même, par la première détermination, de sa contradictoire, c’est-à-dire par auto-négation. Le procès logique d’actualisation de l’Idée, dans la Science de la logique, débute par une unique catégorie, la catégorie d’Être : Hegel à cette occasion montre que, comme pour Platon, son problème est celui de la détermination progressive de l’indéterminé. En effet, l’Être est défini comme « néant-de-déterminations ». De là, l’Être « passe » immédiatement dans le néant, pure absence de déterminations : Être et néant sont à la fois identiques et différents. Or ce passage du même dans son autre, voilà chez Hegel la figure primitive du devenir, qui est donc la troisième déterminité/catégorie engendrée dans le procès logique : et c’est ici la première détermination du « néant-de-déterminations » antérieur.

Ici, c’est bien l’Un-être primitif, de façon immanente à lui-même, qui produit la figure matricielle de la multiplicité, c’est-à-dire la dyade, la dualité (entre être et néant). Le procès de détermination s’enracine ici dans l’Un qui se nie lui-même. L’auto-négation de l’Être comme Un pur est donc la condition sine qua non du procès chez Hegel, et puisque ce procès logique-dialectique produit la multiplicité dans l’immanence d’un principe unique, le moteur du procès doit être immanent à ce principe : ce ne peut donc être qu’un principe d’auto-différenciation, c’est-à-dire une négativité interne, dont la contradiction est la forme principale. Voilà ce qui explique la prégnance de l’opérateur « Aufhebung » : elle est le retour à soi, enrichi de nouvelles déterminations, de cet Un-Universel qui s’est temporairement auto-scindé.

C. L’origine de la dualité Même-Autre

La grande différence entre Lautman et Hegel se situe finalement à ce niveau, au sujet de l’origine de la dualité entre l’identité et la différence, le Même et l’Autre. Derrière les couples de notions qui constituent les Idées, on a en amont chez Platon et chez Lautman celui de l’Un et de la Dyade (qui est le prototype du multiple et de l’altérité), c’est-à-dire celui du Même et de l’Autre.

Or, pour « la méthode platonicienne de division, telle que l’enseignent le Sophiste et le Philèbe »,

L’unité de l’Être est une unité de composition et un point de départ vers la recherche des principes qui s’unissent dans les idées[39].

Cette thèse d’une unité de « composition » est radicalement anti-hégélienne. Mais pour Lautman, c’est clair : le Même et l’Autre sont deux principes ontologiques d’emblée distincts, et en rien l’auto-déploiement différencié d’un même principe. Bref, contrairement à Hegel, Lautman ne produit pas la dualité, il se la donne. Même-Autre, Mouvement-Repos, sont des « genres » primitifs de l’Être, qui communiquent entre eux et se composent, comme l’enseignait le Sophiste[40]. Ainsi, dès lors que l’on se donne, que l’on pose les deux principes, il n’y a pas besoin d’Aufhebung ni de contradiction interne, puisque ces deux opérateurs ne font sens que s’il n’y a qu’un seul principe. On peut se rappeler aussi cette affirmation de 1946 de Symétrie et dissymétrie en physique :

[D]ans le monde intelligible le rôle de l’Idée de l’Autre est d’assurer, par son mélange avec le Même, à la fois la liaison et la séparation des genres. Cette référence à Platon permet de comprendre que les matériaux dont est formé l’Univers ne sont pas tant les atomes et les molécules de la théorie physique que ces grands couples de contraires idéaux comme le Même et l’Autre, le symétrique et le dissymétrique, associés entre eux selon les lois d’un harmonieux mélange[41].

Concluons cette partie sur une dernière remarque. Pour assimiler pleinement la position de Lautman à celle de Hegel, il faudrait assimiler « l’Autre » platonicien à son « négatif » à lui, ce à quoi très exactement procède Hegel dans ses Leçons sur Platon[42]. Autrement dit, seule la validité de l’interprétation hégélienne de Platon permettrait d’apparenter Lautman à Hegel, ce qui est justement stricto sensu intenable. Quoi que l’on fasse en matière de réhabilitation de Hegel en matière épistémologique, comme c’est notre cas, il est tout à fait impossible de le suivre sur ce point névralgique.

II. D’une divergence conceptuelle à une convergence formelle : le paradoxe de la formalisation des dialectiques de Lautman et Hegel

1. De C. Ehresmann à F. Zalama : l’esprit catégoricien de la dialectique lautmanienne

Lors de la discussion de la séance de la Société française de philosophie du 4 février 1939, le mathématicien C. Ehresmann, promoteur dès les années 1950 en France de la théorie des catégories (née une décennie plus tôt), dit la chose suivante :

J’ai noté quelques réflexions qui se rapportent à la thèse de M. Lautman […] je cite une des phrases les plus caractéristiques : « Une des thèses essentielles de cet ouvrage affirme la nécessité de séparer la conception supra-mathématique du problème des liaisons que soutiennent entre elles certaines notions, et la découverte mathématique de ces liaisons effectives au sein d’une théorie. »

Si j’ai bien compris, il ne serait pas possible, dans ce domaine d’une dialectique supra-mathématique, de préciser et d’étudier la nature de ces relations entre les idées générales. Le philosophe pourrait seulement mettre en évidence l’urgence du problème.

Il me semble que, si nous avons le souci de parler de ces idées générales, nous concevons déjà d’une façon vague l’existence de certaines relations générales entre ces idées ; dès lors, nous ne pouvons pas nous arrêter à mi-chemin ; nous devons nous poser le problème vraiment mathématique qui consiste à formuler explicitement ces relations générales entre les idées considérées[43].

Et un peu plus loin,

Je pense que les problèmes généraux soulevés par M. Lautman peuvent s’énoncer en termes mathématiques, et j’ajouterai que l’on ne peut s’empêcher de les penser en termes mathématiques[44].

Sans télescoper les périodes — Lautman n’a pas connu la théorie des catégories —, c’est en suivant cette exigence d’Ehresmann que F. Zalamea invite à traduire aujourd’hui dans la théorie des catégories toute la combinatoire d’opérateurs philosophiques de Lautman. Et c’est là selon moi que revient au centre le rapport Lautman-Hegel, puisque ce que F. Zalamea propose n’est rien d’autre que ce qui a déjà été tenté avec Hegel, à diverses reprises et dans d’autres idiomes théoriques : une formalisation de la dialectique. Rappelons l’énoncé liminaire qui a déterminé l’orientation de Lautman (l’impossibilité de l’auto-fondation technique de la mathématique dans le Programme de Hilbert, impossibilité sanctionnée par le théorème d’incomplétude de Gödel de 1931) :

Dans la métamathématique d’Hilbert, on se propose d’examiner les théories mathématiques du point des notions logiques de non-contradiction et d’achèvement[45], mais ce n’est là qu’un idéal vers lequel s’orientent les recherches, et l’on sait à quel point cet idéal apparaît actuellement comme difficile à atteindre. La métamathématique peut ainsi envisager l’idée de certaines structures parfaites, réalisables éventuellement par des théories mathématiques effectives… […] idées abstraites que nous proposons d’appeler dialectiques[46].

Un instructif aller-retour est donc en train de se produire : Lautman avait transposé au plan métaphysique la métamathématique technique d’Hilbert à cause des impossibilités auxquelles elle se heurtait ; F. Zalamea veut re-transposer au plan technique la métamathématique métaphysique de Lautman, en l’espèce en théorie des catégories[47]. La différence de nature entre la rigueur philosophique et l’exactitude scientifique a toujours tendance à s’amenuiser dès qu’on se trouve au plan des fondements ou de la fondation, par essence complexe et hybride. Voici ce que F. Zalamea affirme :

Les « schémas de structure » lautmaniens devancent (dans leur conception) la technique mathématique de son époque, et ils peuvent être nettement précisés seulement dans le contexte plus tardif de la théorie des catégories. Les schémas, la dialectique, le couple Même/Autre, les idées et les mixtes platoniciens acquièrent une notable exactitude technique grâce aux notions de diagramme, objet libre, foncteur représentable et pair adjoint de la théorie des catégories[48].

Les « notions » peuvent être précisées grâce aux constructions catégoriciennes libres (diagrammes, limites, objets libres), les « idées » grâce à l’élévation de classes d’objets libres en paires de foncteurs adjoints, les hiérarchies dialectiques grâce aux échelles de niveaux dans les transformations naturelles[49].

La théorie des catégories n’est pas une théorie d’objets, mais une théorie de structures plus larges, plus intuitives que les ensembles, par exemple, qui sont « au-delà des objets » : les catégories sont des collections d’objets et de flèches (morphismes) composables entre elles et allant d’un objet-source vers un objet-but. La théorie met évidemment l’accent sur les morphismes (dont les « transformations naturelles » sont un type particulier) par lesquels une structure peut être préservée. De là elle étudie la façon dont un édifice algébrique plastique sous-tend des univers mathématiques variés, leur variation reposant sur des spécifications progressives des catégories les plus vastes génériques vers les plus restreintes. Elle est ainsi à même d’objectiver les « va-et-vient », les traductions, entrecroisements, expressions mutuelles, imports-exports de méthodes qui peuvent s’opérer entre des configurations techniques déterminées, tout cela formant une vision précise de l’unité opérationnelle des mathématiques. Les accents lautmaniens de tous les aspects de cette nouvelle théorie de l’un et le multiple sont effectivement indubitables.

Est-ce Lautman qui est pré-catégoricien, ou la théorie des catégories qui est d’esprit lautmanien ? Les deux formules se trouvent sous la plume de F. Zalamea. Dans tous les cas, l’essentiel, c’est le rôle de la dualité et de la structure : l’approche catégoricienne est l’objectivation-description technique primitive des relations structurelles[50], des « schémas de structures », des opérations duales ou de dualisation qu’entretiennent entre eux des objets variés, ce qui correspond à l’antithétique des Idées-couples. L’idée est fort stimulante, d’autant que, conformément au Timée dont il se réclame, Lautman estime que le monde sensible-phénoménal, comme les théories mathématiques, sont autant de « modèles » des structures dialectiques[51].

La section qui suit vise à mettre doublement en perspective cette proposition extrêmement stimulante, d’abord en la rapprochant des formalisations de la dialectique hégélienne, ensuite en revenant sur les enjeux communs de ces entreprises convergentes.

2. Formaliser la contradiction dialectique

Diverses tentatives de « formalisation de la dialectique » hégélienne ont été tentées au siècle dernier, visant d’abord à légitimer techniquement la négativité et l’idée d’une contradiction interne non stérile. G.-G. Granger dans Formes, opérations, objets de 1994, affirme, en plus d’un rejet sans appel de toute dialectique autre que descriptive et seconde, qu’au mieux une logique formelle dialectique sera consistante, mais en tous cas pas plus féconde que la logique standard. C’est peut-être vrai, mais présentement ce n’est pas le problème : il s’agit pour nous surtout de mesurer les enjeux et les significations de l’entreprise.

Le système de Doz et Dubarle : Logique et dialectique de 1972

Parmi ces diverses tentatives[52] de démonstration que la négativité hégélienne n’est pas incompatible avec la rationalité logico-mathématique, la plus instructive pour nous, c’est celle de A. Doz et D. Dubarle, datant de 1972 et consignée dans leur ouvrage Logique et dialectique[53]. Leur initiative ressemble d’abord à une profession de foi quasi-logiciste :

La philosophie, si elle veut atteindre à la rationalité qu’elle a en vue, doit elle aussi soumettre son discours au contrôle d’une logique, qui, en elle-même, a tous les caractères d’une théorie mathématique. Car la logique […] est par principe une mathématique commune à toute pensée rationnelle[54].

D’autre part selon eux, si

quelque régularité dans les dispositions discursives se dévoile de façon plus ou moins manifeste, alors, de par sa nature même, cette régularité se présentera sous les espèces d’un schéma sujet à mathématisation[55].

1. Triplicité et quadruplicité des moments du concept

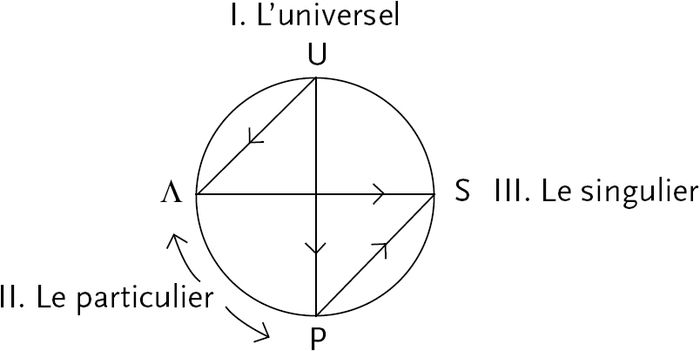
Les auteurs rappellent que le concept

est toujours pour la logique hégélienne […] cette unité complexe et organisée de trois moments qui lui confèrent une structure interne : le moment du concept universel, celui du concept particulier et celui du concept singulier. Ces trois moments sont absolument immanents les uns aux autres dans l’unité indéchirable du concept. Mais si l’idée est nette, elle demande à être examinée et discutée de près avant de pouvoir être […] traduite en pensée d’une structure mathématique susceptible de fournir la base d’un véritable formalisme logique[56].

Autrement dit, bien que le Concept hégélien possède une « architecture quasi mathématique[57] », sa formalisation ne va évidemment pas de soi, dans la mesure où le concept hégélien a « ses différences conceptuellement au-dedans de lui-même[58] ». Or voilà quelle est la véritable difficulté qui surgit de cette dimension : manque à la triplicité hégélienne Universel/Particulier/Singulier, par laquelle le concept est toujours unité-totalité, le terme nul, celui qui serait assimilable au zéro ou au vide, c’est-à-dire algébriquement le résultat de l’intersection de deux termes complémentaires, apte à capter le moment strictement négatif de ces « différences » immanentes au concept. D’où une décision théorique décisive :

Mais pour qu’une mathématique logiquement exploitable de l’unité et de ses moments internes puisse avoir lieu, il semble indispensable que la pensée s’adjoigne cette terminaison conceptuelle vide qui désigne le « néant abstrait » (abstrakte Nichts), ainsi que le dit Hegel, jouant fonctionnellement le rôle du zéro. […] C’est cette adjonction d’un terme nul […] que, contre Hegel (il ne faut pas s’en cacher) l’on va postuler ici pour libérer la puissance de formulation mathématique que l’enseignement hégélien contient en lui, mais comme à l’état paralysé[59].

D’où le passage de la triplicité à la quadruplicité Universel/Particulier/Singulier/terme nul. Ce dernier est noté Λ, la quadruplucité elle {U,P,S, Λ}. Λ, considéré comme antinomique avec la totalité, est « à sa façon » posé comme moment et terminaison du concept. Du reste, les auteurs insistent sur deux choses : d’une part, Hegel aurait lui-même senti la nécessité de ce « dédoublement », renvoyant à l’auto-différenciation, c’est-à-dire l’auto-dualisation de l’Universel abstrait. À l’appui le passage suivant (c’est nous qui ajoutons entre crochets les lettres du quadruplet {U,P,S,Λ}, à des fins de clarté) :

Cette négativité, entendue comme la contradiction se sursumant, est l’établissement de l’immédiateté première, de l’universalité simple ; car c’est immédiatement que l’autre de l’autre, le négatif du négatif, est le positif, l’identique, l’universel. Ce second immédiat [S], si après tout l’on veut compter les moments est dans la totalité du circuit dialectique le troisième moment par rapport au premier immédiat [U] et au moment médiat [P]. Mais il est aussi le troisième moment vis-à-vis du premier négatif ou négatif formel [P] et de la négativité absolue ou second négatif [Λ]. Dans la mesure où maintenant ce premier négatif est déjà deuxième terme, alors celui qui est compté comme troisième [S] peut aussi être compté comme quatrième et la forme abstraite être prise comme quadruplicité au lieu de l’être comme triplicité. De cette façon le négatif ou la différence est compté comme une dualité[60].

Λ, terme nul, est donc la « négation absolue » dans le texte. C’est cette quadruplicité qui va organiser la nouvelle formalisation, laquelle est préparée par une « schématisation ». Mais le futur formalisme, tout en se fondant sur cette quadruplicité, devra néanmoins coller au plus près du sens dialectique de cette auto-différenciation, c’est-à-dire du fait que

la différence de l’universel […] doit être intérieure à l’universel et non se prendre en dehors de celui-ci[61].

Notons que si Dubarle justifie, contre Hegel, la formalisation de cette schématisation, il ne choisit pas pour autant n’importe quelle structure conceptuelle de la Science de la logique : des modalités du dialectique que sont le passage (Être), la réflexion (Essence) et le développement (Concept), c’est la troisième (l’auto-dépassement de l’universel dans le singulier par la médiation du particulier) qu’il retient, arguant de son universalité supérieure par rapport aux autres. Nous pouvons maintenant donner un aperçu synthétique du système formel que les auteurs instituent sur ces bases, et qui va fixer avec certaines contraintes, d’abord dans leur « schématisation » puis dans leur « formalisation », l’expression des opérateurs dialectiques homologués aux transitions conceptuelles majeures de la Science de la logique, avec au centre l’auto-négation et l’Aufhebung.

2. La schématisation

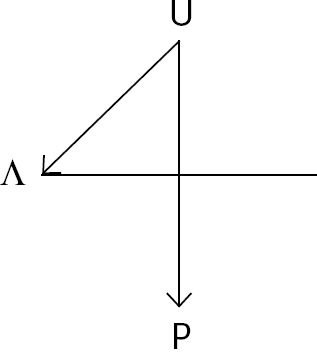
Formaliser une transition dialectique nécessite une double opération, correspondant à l’effectivité du négatif dialectique et à celle de l’auto-différenciation de l’universel abstrait. Une transition inclut donc une négation opposant par exemple A à son autre A’, et un rapport interne à A entre ce qui est conservé et ce qui est dépassé. Il y a deux transitions dialectiques mettant en jeu {U,P,S,Λ} : pour les objectiver, Doz et Dubarle, commencent par « schématiser » le dispositif, c’est-à-dire en tracer les relations générales, épurées, dites « algébrico-logiques »[62], ce qui donne la charpente suivante :

où U’ = P et Λ’ = S : les relations horizontale et verticale figurent la négation classique (complémentation).

La première transition est celle qui va de l’universel abstrait au particulier : c’est une opération double, moment de négation, de scission interne de l’universel U, qui le distribue en son contradictoire logique P, et le suspend simultanément dans le terme nul Λ. Elle se note U → (Λ,P) :

La seconde transition, elle, va du particulier à l’universel concret, noté (Λ, P) → S :

Dans les termes généraux des moments du Concept, la figure du singulier accompli est ainsi :

Figure 4

**Schéma global de l’Aufhebung**

Les jeux de ces triplicités enchevêtrées dans la quadruplicité primitive traduisent pour Dubarle le fait que le Concept, qui est Un, peut être considéré, « bien que de façon extrêmement triviale en sa détermination explicite, [comme] une entité mathématique[63] ». Ces « schémas », ces épures, doivent maintenant être formalisés.

3. La formalisation

Associer la logique classique et l’essentiel de « l’économie interne » du procès de l’Aufhebung conduit les auteurs à instituer un système formel qui est une extension de la logique classique des termes (de style Boole-Schröder), et non directement de la logique des propositions et celle des prédicats qu’ils estiment inadéquates à l’esprit de la logique hégélienne : celle-ci est une logique du concept, pas de la distribution de valeurs de vérité, et plus précisément une logique du mouvement de sa structure interne. D’où l’intérêt porté seulement sur les extensions et les intersections (au sens large) des termes. Le langage, la définition des formules par un nombre fini de clauses récursives, et le jeu d’axiomes[64] et de règles d’inférences choisis, relèvent spécifiquement de la logique propositionnelle, de la logique booléenne et de la logique ultra-booléenne (dans l’ordre de complexité)[65].

i. Éléments syntaxiques

Cette logique des termes notionnels contient donc d’une part des termes spécifiques :

Λ : terme nul
V : Univers du discours.
U et P : universel, particulier.

A, B, C, etc. : termes indéterminés (classes, ensembles, concepts, etc.).

D’autre part, aux opérateurs logiques usuels (union, intersection, complémentation, différence symétrique) sont ajoutés deux nouveaux opérateurs monadiques :

△, opérateur dit « d’abstraction »
▽, opérateur dit de « déposition »

tels que

△▽A = ▽△A = Λ

Ces opérateurs sont strictement complémentaires. L’idée générale est que tout terme conceptuel indéterminé doit être compris comme assemblant quelque chose qui relève de la constante U, et quelque chose qui relève de la constante P. On définit ainsi deux nouvelles opérations assimilables à des opérations générales d’abstraction, séparant dans le terme A ce qui relève de ces deux couches conceptuelles respectives, et inverses l’une de l’autre : △A désigne l’opération représentant le moment d’universalité U de A, appelée « abstraction » au sens strict, alors que ▽A désigne l’opération représentant le moment de particularité P de A, appelée « déposition » au sens strict. On note A’ le complémentaire de A : par définition, les opérations △A et ▽A sont des processus « relativisés » à A, d’où l’introduction par les auteurs d’une règle opératoire complémentaire, dite de « relativisation ». Dès que l’on considère une opération dans le cercle d’un terme A précis, comme la négation d’un terme X, celle-ci s’opère par « relativisation à A » par l’opération

A ⋂ X’

Techniquement, le système est une algèbre ultra-booléenne de rang 2, dont la structure est la plus simple des algèbres ultra-booléennes[66], extension consistante de la logique booléenne. Voilà pour la mise en situation du « formalisme logico-mathématique » « dérivé du système hégélien »[67].

Déroulons maintenant les rapports essentiels entre les opérateurs. D’une part :

▽ A =A ⋂ (△ A) ʹ
= A ⋂ (A ⋂U) ʹ
= A ⋂ (A ʹ ⋃ U ʹ)
= A ⋂ (A ʹ ⋃ P)
= (A ⋂ Λ) ⋃ (A ⋂ P)
= Λ ⋃ (A ⋂ P)
D’où : ▽ A = A ⋂ P

D’autre part :

△ A = A ⋂ (▽ A) ʹ
= A ⋂ (A ⋂ P) ʹ
= A ⋂ (A ʹ ⋃ P ʹ)
= A ⋂ (A ʹ ⋃ U)
= A ⋂ (Λ ⋃ U)
= (A ⋂ Λ) ⋃ (A ⋂ U)
= Λ ⋃ (A ⋂ U)
D’où : △ A = A ⋂ U

△A et ▽A sont donc bien respectivement le moment d’universalité et le moment de particularité de A. On a ainsi deux égalités fondamentales :

△ A ⋃ ▽ A = A
△ A ⋂ ▽ A = Λ

△ A et ▽ A vont ainsi former le couple de moments logiques conjugués et opposés, couple qui fournit un modèle logique de « contradiction » interne à un concept A.

ii. Expression formelle des transitions conceptuelles

On peut maintenant réécrire la première transition U → (Λ,P) en △A → (Λ,▽A), avec le schéma suivant :

Figure 5

**Formalisation de la première transition conceptuelle**

Cette transition repose sur deux opérateurs α et β, respectivement de « déposition » et de négation, tels que, dans les termes du schéma initial,

αU = △U = Λ
βU = U’ = P

Ce qui donne ici

déposition[68]
α△A = ▽(△A) = Λ

complémentation-négation de △A relativisée à A
β△A = A⋂(△A)’ = A⋂P

La seconde transition (Λ,P) → S se réécrit elle en (Λ,▽A) → A :

Figure 6

**Formalisation de la seconde transition conceptuelle**

Cette fois, la transition se décompose en ces deux opérateurs γ et δ, respectivement de négation et de « relèvement », tels que, dans le schéma initial,

γΛ = Λ’ = S
δP = (▽P’)’ = P⋃U = S

D’où ici :

complémentation-négation de Λ
γΛ = Λ’ = A

relèvement relativisé[69] à A de ▽A
δ▽A = A⋂(▽A’)’
= A⋂(A⋃U) = A (par absorption)

On a donc :

γΛ = δ▽A = A

Or par définition △A⋃▽A = A, id est P⋃U = S. Déposition et relèvement amènent bien à la totalisation des moments logiques du concept en l’universel concret qu’est le singulier A. Le relèvement se définit donc par la négation d’une déposition (en l’occurrence, la particularisation de la négation de l’universel concret), c’est-à-dire, ici, négation relativisée à A (c’est-à-dire négation déterminée) de la négation de l’universel par le particulier. L’articulation entre « déposition » et « relèvement » fournit ainsi un modèle logique de l’Aufhebung.

III. Le pullback de l’Aufhebung, et le destin formel du négatif

Maintenant qu’est présenté l’essentiel du dispositif, on peut énoncer la chose suivante : ce modèle logique de l’Aufhebung semble littéralement reformulable dans l’idiome catégoricien, ce qui n’est pas sans être paradoxal, puisque cela pourrait indiquer que, formellement parlant, les deux dialectiques de Hegel et de Lautman n’ont pas de différence essentielle, alors qu’on a vu en I que c’est le cas. Ce qui suit vise donc d’une part à attester de cette possibilité de traduction en en esquissant quelques éléments, et à dérouler les implications de cette traductibilité. Nous comptons par avance sur les lecteurs intéressés pour qu’ils nous aident ensuite à approfondir la chose, en quelque sens que ce soit — donc aussi qu’ils nous remettent dans le droit chemin si cette esquisse ne tient pas la route.

A. L’Aufhebung « à la catégoricienne »

Les transitions conceptuelles fondées sur la négativité reviennent au jeu entre trois pôles, ceux de l’Universel, du Particulier et du singulier, et d’une négativité elle-même relue comme une dualité : le système d’objets et de foncteurs est une « quadruplicité » dont les relations peuvent se traduisent aisément en pullback. Certes, celui-ci n’est qu’une construction universelle parmi d’autres, mais, d’une part, pour reprendre R. Goldblatt,

The pullback is a very important and fundamental mathematical notion, that incorporates a number of well known constructions. It is certainly the most important limit concept to be used in the study (and definition) of topoi[70].

D’autre part, c’est le type de construction auquel se prête le plus immédiatement le dispositif de Doz-Dubarle. La configuration de la figure 4 « Schéma général de l’Aufhebung » peut en effet se présenter sous la forme suivante :

Le pullback de l’Aufhebung — Figure 7

Le pullback de l’*Aufhebung*

Ce diagramme explicite le produit fibré au-dessus de S :

U = Λ × _SP

Ce produit est le « pullback » des flèches δ et γ , où U est l’objet initial et S l’objet central. Soit A : U → S pour « Aufhebung ». On a donc

δ(β(U)) = γ(α(U) = S.

C’est-à-dire :

A = γ ∘ α = δ ∘ β

Le carré est bien commutatif.

Résultat : le pullback de A proposé pour {△A,▽A,A, Λ} moyennant relativisation à A de {U,P,S,Λ} et {α,β,γ,δ}, est le pullback de l’Aufhebung par lequel s’opère le développement dialectique du terme (ou concept) A.

Une question « sémantique » : quid des domaines et codomaines ?

Au début de la schématisation Doz et Dubarle écrivent que

[il] est bien entendu que ces quatre terminaisons ou moments logiques ne constituent toutes ensemble qu’un seul Concept, la question de l’intériorité ou de l’extériorité mutuelle des divers moments du Concept étant pour le moment hors de propos et neutralisé[71].

Corrélativement, on sait que le schème dialectique (de la schématisation) vaut pour tout terme conceptuel. Il faut donc, au niveau sémantique, combiner cette universalité, et à la fois l’intériorité conceptuelle des moments, et leur nécessaire extériorité technique. Pas nécessairement pour statuer sur la nature mathématique à attribuer à U, P, S et Λ, mais au moins pour expliciter leurs domaines et co-domaines, afin que ce rapprochement ne soit pas simplement suggestif. Les vertus de l’abstraction, des procédés de représentation et de hiérarchisation de modèles permis par la théorie des catégories font qu’une catégorie est avant tout un univers du discours mathématique spécifié par la présence en lui d’un certain type d’objets et un certain type de fonction ou application entre ces objets[72], l’essentiel n’étant pas la nature de ces éléments, mais la façon dont ils se comportent entre eux, s’opposent, s’impliquent ou se composent, etc.

A, B, C, etc. sont des « notations d’indéterminées », des termes indéterminés quelconques, « dont la nature est caractérisée suivant le rang de la logique des termes envisagés[73] », détermination insuffisante au niveau sémantique. Au sens large, {U,P,S,Λ} sont donc des constantes logiques et {α,β,γ,δ} des foncteurs invariants par relativisation, de l’Univers des termes. Si ce diagramme de la fig. 7 fait sens pour ce qu’on pourrait appeler la catégorie générale des concepts dialectiques, synonyme d’« Univers des termes », ses objets sont ces « moments » ou pôles conceptuels, et les morphismes ces « transitions conceptuelles ». Qu’en est-il alors des domaines et co-domaines des objets et foncteurs ? Un élément important nous est donné : une propriété élémentaire fixée dans le système (par voie axiomatique au besoin)[74], c’est :

△A ⊂ A

où ⊂

généralise, en l’appliquant aux termes notionnels présentement envisagés, la notion de la relation d’inclusion booléenne. On continuera d’appeler cette relation relation d’inclusion[75].

On a logiquement aussi ▽A ⊂ A. Rappelons que {△A,▽A,A, Λ} sont des moments-pôles de A en tant que complètement développé (i.e. S relativisé à A) : A est donc à la fois la totalité du diagramme en tant que résultat d’une composition d’applications, c’est-à-dire son objet central, et un pôle du diagramme. A est donc un « pôle-objet but », par rapport auquel les trois autres pôles, qui au sens large sont les domaines d’opérativité des foncteurs, des pôles, sont assimilables à des sous-objets, en vertu de cette relation généralisée d’inclusion. Les pôles sont à la fois argument et domaine de définition des foncteurs : le domaine est tout autant l’input, l’argument, et le co-domaine tout autant l’output, la cible (target). Si l’on considère par exemple (cf. fig. 7)

Ici le pôle-domaine ▽A, pôle de particularité de A, est donc en vertu de la proposition ▽A ⊂ A assimilable à un « sous-ensemble » du codomaine A, donc à un sous-objet de A, ce qui implique que δ est injectif.

En résumant et généralisant, on voit bien ici qu’un enjeu central de cette détermination sémantique, c’est l’établissement précis des propriétés mathématiques des foncteurs. Comme la conceptualité dialectique est une conceptualité qualitative, et en raison de cette relation d’inclusion généralisée, on pourrait éventuellement penser à une traduction topologique du dispositif. On revient sur d’autres aspects de cette indétermination au § C ci-dessous.

B. La piste Lawvere

Lawvere a toujours manifesté un puissant intérêt, qui ne s’est jamais démenti, pour une tentative consonante de formalisation catégoricienne de l’unité et identité des opposés (unity-and-identity-of-opposites), c’est-à-dire de l’Aufhebung. En 1991, dans l’article « Some Thoughts on the Future of Category Theory », il écrit :

Unity-and-identity-of-opposites, the Aufhebung relation between two such within a given unity : this is a […] proposed philosophical guide[76].

La « formulation mathématique spécifique » de l’Aufhebung qu’il vise passe par la clarification de la dimensionnalité en général et des infinitésimaux en particulier, le but étant de capter certains rapports de l’être et du devenir (Being and Becoming), dont on a vu en première partie qu’ils sont chez Hegel, à la source, de l’auto-altération par contradiction interne de l’Un-Être. A partir de l’idée que l’uni-dimensionnalité et la connexion sont des concepts philosophiques, il propose d’interpréter la connexion d’un espace arbitraire donné dans les termes du « niveau minimal » et « hégélien » des « figures » situées dans cet espace. En résumé, l’Être devient pour lui une catégorie stratifiée en « niveaux » (levels), c’est-à-dire une échelle de niveaux (comme l’évoque F. Zalamea dans la citation du début de section) qu’il propose d’identifier aux dimensions, pour ensuite « determine what the general dimensions are in particular examples[77] ». Chaque niveau étant alors la donnée de deux catégories et d’un morphisme « descendant » (downward) de la première (large) vers la seconde plus petite et munie de deux opérateurs adjoints tels que

Such a pair of categories and triple of functors is a unity-and-identity-of-opposites (UIO) in the sens that the big category unites the two opposites subcategories which in themselves are identical with the smaller category[78].

Voilà pour l’orientation technique générale (nous laissons ici au lecteur le loisir d’approfondir les développements et précisions qu’en donne Lawvere), où l’on voit bien aussi que la question sémantique est centrale. Nous pousserons plus avant nous-mêmes l’étude en d’autres lieux, en particulier la détermination du degré d’affinité mathématique que le dispositif de ce dernier peut entretenir avec le pullback proposé ci-dessus.

C. Questions laissées en suspens

Pullback dans une catégorie, ou entre catégories ?

Dans la lignée de ce qui précède, on peut dire que l’une des questions qui se pose est celle de savoir si l’on a affaire, précisément, à un pullback dans une catégorie ou d’un pullback entre catégories distinctes. Le pullback est dans un topos chez Goldblatt, alors que chez Lawvere la question se pose plus en termes de foncteurs adjoints entre des catégories. Il est essentiel de voir qu’en l’état le pullback tiré du dispositif hégélien formalisé est en fait à mi-chemin entre la métaphore et un véritable début de formalisation : rien chez Hegel ni chez Doz-Dubarle ne peut vraiment aider pour répondre à cela. En hégélien on pourrait répondre que le pullback est à l’intérieur d’une même catégorie, dans la mesure où le dispositif tente d’expliciter le comportement dialectique de l’auto-négation d’un même concept. Mais cela ne serait pas une réponse de logicien ou de mathématicien, ni de philosophe, mais plutôt… d’apprenti-sorcier.

D’un autre point de vue, on peut voir très clairement dans cette indétermination l’état même de la question de la signification ou de la pertinence « sémantique » de l’opération de formalisation : il nous semble que justement seul le passage au formel peut trancher, au sens où le plan philosophique lui-même n’apparaît pas comme le lieu pertinent de la décision. D’un autre point de vue et corrélativement, la question de savoir si c’est, techniquement parlant, à l’intérieur d’une catégorie ou entre des catégories que la chose se joue reste pour cette raison totalement ouverte : l’étude initiée ici mérite d’être dûment approfondie pour qu’elle donne prise à une décision digne de ce nom.

En d’autres termes, l’essentiel ici, pour nous, était de contribuer à poser un problème — les formalisations de la dialectique manquent-elles ou non le noyau conceptuel principal qu’elles s’efforcent de capter ? — et d’en cerner les premières implications, et non de tenter prématurément, en l’absence des outils adéquats, de le résoudre.

Où tout cela a-t-il lieu ? Du problème logico-mathématique au problème philosophique

Ce problème du statut, des contraintes et de la signification logico-mathématique de la « traduction » du système de Doz et Dubarle dans le cadre catégoricien, et même dans le cas d’une « simple » affinité de structure reposant sur la traduction de l’Aufhebung, par une configuration à quatre éléments, est un problème essentiellement logico-mathématique, portant, pour faire bref, sur les rapports précis que peuvent entretenir les deux systèmes formels. Ce qui n’est pas à confondre avec le problème philosophique de la formalisation même de l’Aufhebung et de la capacité de la première à capter le noyau rationnel de la seconde.

En ce qui concerne le premier problème, en vertu même des limites du présent travail, on peut du moins tenter de généraliser sa portée avec l’alternative suivante. Esquisser la traduction du système de Doz-Dubarle, qui est une algèbre ultra-booléenne, en théorie des catégories implique-t-il que nous soyons face à un pullback dans la catégorie particulière des algèbres ultrabooléennes ? Cela reviendrait logiquement à intégrer ce système dans la théorie des catégories, la traduction du premier dans la seconde étant alors seulement une reformulation en local. Autrement dit, si l’on peut voir dans le dispositif une « catégorie » à quatre « objets » {U,P,S,Λ} et à une « propriété universelle » délimitée par ses quatre « foncteurs » {α,β,γ,δ}, peut-être est-il simultanément nécessaire de voir, ce qu’indiquerait la systématicité des guillemets, qu’on a simplement affaire à une simple façon de parler, de présenter les choses : auquel cas la seule chose tangible ici, en l’absence de caractéristiques précises supplémentaires, ce serait cette « affinité » générale descriptivement parlant, de structure (et donc l’absorption possible du premier dans la seconde). Mais si au contraire l’on considère le système de Doz-Dubarle et la théorie des catégories comme deux cadres distincts, ce n’est pas en termes d’intégration que le problème se pose : la traduction n’est pas alors une « reformulation », mais plutôt une opération générale de mise en équivalence, et dans ce cas il faut démontrer l’exactitude de l’équivalence (comme pour toute affirmation d’équivalence entre deux systèmes formels distincts). Ce qui impliquerait alors, entre autres, que la théorie des catégories n’est pas considérée comme un langage universel, mais plutôt comme une théorie parmi d’autres, ce qui est une thèse, et non une évidence. En tous cas, dans les deux cas, un approfondissement technique et conceptuel conséquent sera nécessaire.

Mais le plus important ici à nos yeux est que les acquis, aussi minimes soient-ils, de cette analyse du problème logico-mathématique éclairent notablement le problème philosophique.

D. Retour final sur la dualité : le sort fait au négatif

En effet, au niveau « technique » où nous en sommes arrivés, cette affinité de structure, cette traductibilité « grossière » du dispositif de Doz-Dubarle dans l’idiome catégoricien montre la chose suivante : du point de vue des formalisations respectives, effectuées ou esquissées, du noyau de leurs dialectiques respectives, rien ne permet de façon tangible de séparer ou distinguer Hegel de Lautman. Cette convergence n’a rien d’anodine et exige une première distinction essentielle, qui est la suivante : que philosophiquement Hegel et Lautman se séparent sur l’origine de la dualité (avec toutes les conséquences philosophiques que l’on a évoquées ou qui pourraient l’être) n’empêche pas qu’ils travaillent tous les deux de facto avec la dualité, dont la quadruplicité de l’Aufhebung revisitée comme du dispositif catégoricien est évidemment un produit dérivé, et dont la bivalence classique est bien l’indice probant.

La fin de citation ci-dessus de Hegel dit bien :

Le négatif ou la différence est compté comme une dualité.

Tout est là : c’est l’hypostase seule de ce choix qui permet de formaliser Hegel et de l’apparenter à Lautman, et qui rend possible cette convergence « catégoricienne ». Mais en second lieu, conceptuellement parlant, être « strictement » hégélien et non platonico-lautmanien — on l’a vu en conclusion du I — implique justement de ne pas compter le négatif comme une dualité[79].

D’où, en l’état, la permanence d’un hiatus irréductible entre les deux ordres (le formel et le dialectique), bien que celui-ci soit substantiellement réduit : la convergence (de près ou de loin) des deux entreprises de formalisation repose sur une décision inaugurale de Doz et Dubarle qui va contre Hegel puisque celui-ci a toujours défendu cette irréductibilité de l’ordre conceptuel spéculatif (dialectique) à toute captation technique (analytique), aussi sophistiquée soit-elle. Ce hiatus peut indiquer, de ce fait, que la formalisation de l’Aufhebung manque purement et simplement l’Aufhebung, conclusion qui serait celle de Hegel, pour qui l’entendement analytique est justement ce qui ne comprend pas qu’une logique conceptuelle autre et qualitativement distincte oeuvre au-delà de lui. Mais d’un autre côté on pourrait imaginer dire que l’exercice de la formalisation, et plus largement le travail logico-mathématique, dans son « exactitude », ne porte pas sur l’origine. Doz et Dubarle écrivent qu’il faut

remarquer expressément que la façon la plus essentielle d’être rationnel dans la condition quantitative qu’il ne peut éviter, c’est, pour un langage humain, de donner lieu à une logique mathématique[80].

ce par quoi il faut entendre logique mathématique classique. Or « classique » rime en dernière instance avec « dualité ». Reste donc le problème-énigme fondateur : même avec la dialectique hégélienne, on retombe ici, certes pas directement sur la bivalence, mais bien sur ce qui semble être encore et toujours la nécessité d’un primat de la dualité. Donc, s’il y a un présupposé commun et transversal à questionner encore et toujours, avec et au-delà de Lautman, aux plans philosophique, mathématique, mais aussi anthropologique voire psycho-cognitif, c’est bien ce principe millénaire de la dualité, qui semble bien être, pour reprendre la formule de J.-M. Salanskis, une « énigme » et non un concept, c’est-à-dire une énigme ouverte à une pluralité de conceptualisations.

« Conclusions » : quelques enjeux du chantier

Cette étude est une invitation, et non une conclusion, dont on peut retenir les issues suivantes.

Les formalisations de la dialectique s’effectuent respectivement, en partie contre l’esprit de Lautman, totalement contre celui de Hegel, comme le savent bien les auteurs — on l’a vu — leur démarche va « contre Hegel (il ne faut pas s’en cacher)[81] ». Cette différence de degré entre Lautman et Hegel tient selon nous, en dernière instance, à ce qui les sépare : leurs conceptions respectives de l’origine de la dualité : primitive chez Lautman reprenant Platon, dérivée de l’Être-Un chez Hegel.
Il y a néanmoins un premier grand mérite à ces formalisations : celui de réduire en partie la difficulté flagrante chez Hegel, moins décelable chez Lautman, mais bien réelle dans les deux cas, qui tient à ce que leurs métadiscours dialectiques entendent, d’une façon ou d’une autre, récupérer en leur ordre le sens de ce que les sciences positives livrent, et maintiennent donc en place, un double régime de vérité. Ces formalisations jettent donc un pont direct entre philosophie et science, en « lissant », bien que l’entreprise soit délicate, complexe et en tension pour les deux régimes de rationalité, et à la condition de se fonder sur une interprétation dualisante de la négativité hégélienne au niveau fonctionnel, au prix de son sens originel, pour le système formel.
Mais il reste que cette expérience de logicisation-mathématisation de la dialectique constitue bien un véritable retournement de situation « dramatique » pour la dialectique, qui semble bien témoigner d’une violence herméneutique au coût élevé. Rappelons un point essentiel : l’indétermination dialectique de l’Idée-couple. Vouloir donner de « l’exactitude » par une traduction technique de la problématique lautmanienne, comme on peut le suggérer en catégoricien, n’est-ce pas comme avec Hegel vouloir l’exactitude là où elle ne peut pas être, n’est-ce pas prétendre déterminer ce qui justement ne peut pas l’être ? Certes, si l’on à l’esprit que la théorie des catégories se présente aussi comme alternative à l’ensemblisme dominant, comme nouveau schème fondationnel des mathématiques, il est certain qu’elle intervient bien en un registre comparable à celui de Lautman. Mais si l’on s’autorise à cette traduction dans un schème ainsi technico-fondationnel, alors il faut prendre la mesure de ce que ce dernier est clairement plus qu’une théorie logico-mathématique parmi d’autres (aussi large soit-elle) dominée par l’exigence « d’exactitude technique ». Ce qui transfère à son sujet le problème du statut et de la nature des formalisations évoquées : théorie-cadre, théorie-discours, elle devient alors méta-théorie et entre de plein pied dans le champ des conceptualisations partiellement méta-techniques, hybrides, qui doivent être examinées comme telles, et dans toute l’ampleur des difficultés que pour cette raison elles soulèvent[82].
Terminons en tempérant ces enjeux et ce « risque ». Nous ne doutons aucunement de la richesse de la formalisation de Doz et Dubarle, de l’acuité et de la fécondité du programme de Zalamea, ni non plus de l’envergure et de la stimulation du Logique des mondes de Badiou. La question n’est sûrement pas aussi « grave » qu’on peut sembler le dire : il est historiquement notoire, rassurant, et indispensable que de tels franchissements de limites, entre petites trahisons et grandes fidélités (ou l’inverse), s’opèrent sous le sceau de l’excitation. L’essentiel est de rester ensemble, que l’on soit mathématicien ou philosophe, lucides sur les enjeux et les implications de l’opération : indiquer les difficultés ou les apories que ces franchissements rencontrent ne signifie aucunement les délégitimer, mais bien au contraire pour nous participer à leur développement.
De ce point de vue là, approfondir le problème logico-mathématique exigera de lever une série d’indéterminations, pointées dans la section III de la seconde partie, et, en particulier, de clarifier le type de « traduction » du système de Doz et Dubarle dans le cadre catégoricien. La traduction est-elle une intégration du premier, moyennant reformulation dans le second, ou mise en « équivalence » des deux ? Question portant en réalité sur les statuts respectivement accordés aux deux dispositifs. Trancher sur ce point névralgique nécessitera de préciser la sémantique propre de la formalisation de Doz et Dubarle, pour progresser dans les caractéristiques proprement mathématiques de ses « foncteurs », « objets », « domaines » et « co-domaines ». Ensuite, par l’autre bout, il faudra dérouler pleinement les propositions catégoriciennes, d’un côté, de Zalamea, de l’autre, de Lawvere, pour mener à bien la comparaison avec la précédente. Enfin, il conviendra de généraliser sur le plan logico-mathématique cette comparaison, notamment par une étude plus vaste des formalisations de visée comparable (avec au premier chef la paraconsistance logique), afin d’être en mesure de dresser un bilan suffisant des vertus et des limites sur le plan philosophique de l’entreprise, laquelle semble en l’état être l’incapacité foncière du formel à se saisir du noyau rationnel de la dialectique : le travail du négatif.

La dualité de Lautman contre la négativité de Hegel, et le paradoxe de leurs formalisationsContribution à une enquête sur les formalisations de la dialectique

Résumé

Abstract

Introduction : deux motifs

I. Pertinence et limite du rapprochement des doctrines de Lautman et Hegel

1. Le problème de la détermination : participation et composition