Article body

1. Introduction

En raison de leur caractère prestigieux et rentable, les études scientifiques à dominante mathématiques sont fortement valorisées par les institutions (Chazal et Guimond, 2003). Selon Pretto et Regnier (2014), la discipline «mathématiques» est particulièrement valorisée à l’école. Or, une faible représentation des femmes est observée dans ce domaine dans le monde en général et au Cameroun en particulier (Fonkoua, 2006; Teague Tsopgny, Maingari et Njopvoui, 2019), à l’heure où la parité hommes-femmes constitue une priorité clairement affirmée et partagée (Toczek, 2005). Pour Costes, Houadec et Lizan (2008) en effet, la place réservée aux mathématiques dans les processus de sélection à l’école a favorisé la différence sexuée d’orientation des élèves. Au Cameroun comme dans de nombreux pays en Afrique et en Europe, les mathématiques jouent un rôle déterminant dans l’orientation des élèves, spécifiquement à partir de la classe de troisième dans l’enseignement secondaire général (Bergeron, 2016; Gueudet, Khaloufi et Marc, 2012). Ainsi, on s’attend à ce que les élèves ayant de bonnes performances en mathématiques choisissent de préférence la voie des mathématiques au détriment de la voie littéraire. Ce qui est plus généralement observé chez les garçons, mais moins chez les filles.

Nombreux sont les auteur·e·s qui soutiennent que les filles ont souvent de meilleures performances scolaires que les garçons, mais accèdent moins aux filières scientifiques les plus prestigieuses et valorisées que ces derniers (Bagès, Martino et Toczek, 2008; Duru‑Bellat, 2004; Plante, Théorêt et Favreau, 2010). Dans cette optique, les recherches restent unanimes sur le fait que les femmes sont largement minoritaires dans les filières scientifiques dominées par les mathématiques. Elles sont en revanche nettement majoritaires dans les filières littéraires où l’enseignement des langues prédomine. C’est le cas par exemple en Europe (Duru-Bellat, 2004; Mosconi, 2004, Morin-Messabel, 2014; Toczek, 2005; Vouillot, 2012a, 2012b), en Amérique (Bergeron, 2016; Marx et Roman, 2002; Plante et al., 2010; Steele et Aronson, 1995) et aussi en Afrique (Bouya, 1993; Fonkoua, 2006; Gastineau et Ravaozanany, 2011; O’Conner, 2001).

Au Cameroun précisément, un rapport du Bureau central des recensements et des études de la population souligne

des disparités relativement importantes du rapport de masculin/féminin autour de la moyenne nationale qui est de 160,4 %; soit 160 garçons pour 100 filles. En effet, les garçons demeurent nettement plus nombreux que les filles dans les filières scientifiques.

BUCREP, 2014, p. 23

C’est dire qu’au Cameroun, dans les séries scientifiques, on compte plus de 60 % de garçons. Pour donner sens à ce résultat, le Rapport d’analyse des données statistiques du ministère des Enseignements secondaires (MINESEC, 2015) situe l’origine de ces disparités au moment des choix opérés par les élèves dans les paliers d’orientation. À l’examen du brevet d’études du premier cycle (BEPC), qui sanctionne la fin du premier cycle de l’enseignement secondaire général (classe de troisième), il y a généralement autant de candidates que de candidats. En 2015 par exemple, on comptait 50,12 % de candidats garçons contre 49,88 % de filles. C’est précisément à partir du second cycle que les disparités de genre commencent à s’observer, du fait d’une spécialisation qui appelle les élèves à opérer un choix entre le domaine scientifique (seconde C) et le domaine littéraire (seconde A). Le même rapport dévoile que, de toutes les filles du second cycle de l’enseignement secondaire général, 62,38 % sont inscrites dans les séries littéraires[1] contre 37,62 % dans les séries scientifiques[2]. En revanche, chez les garçons, près de la moitié se retrouve dans les séries scientifiques. Ce qui présage les grands écarts qu’on observe dans ces disparités au niveau universitaire.

En effet, les filles choisissent moins les mathématiques[3] dans leur programme de formation universitaire. Les statistiques du ministère de l’Enseignement supérieur (MINESUP, 2015) du Cameroun révèlent par exemple qu’à l’université de Yaoundé I où on note le plus grand nombre d’étudiants inscrits en mathématiques, on avait enregistré 84,62 % de garçons contre seulement 15,38 % de filles.

Au regard de ce qui précède, il apparaît clairement que les disparités de genre en matière d’orientation en mathématiques s’observent à l’école, à partir de la classe de seconde. Elles sont rendues aussi apparentes du fait du choix de série qui s’impose aux élèves en amont dans les classes de troisième. Ainsi, intervenir dans l’orientation des filles à partir de ces classes est une mesure qui pourrait s’avérer efficace dans la lutte contre les disparités de genre en mathématiques.

2. Problématique

Les écrits scientifiques sur les difficultés d’apprentissage des mathématiques en général et les disparités de genre en particulier soulignent le rôle de l’enseignant·e de mathématiques dans la motivation des élèves pour les intéresser aux sciences et aux mathématiques (Ivoui, 2001). Dans la même veine, Costes et al. (2008) relèvent l’importance des enseignant·e·s de mathématiques dans l’orientation des filles vers les mathématiques. Cependant, ces recherches n’étudient pas de façon empirique comment les enseignant·e·s peuvent influencer l’orientation des filles vers les mathématiques, surtout dans le contexte africain où les travaux de Bouya (1993)[4] et O’Conner (2001, p. 6)[5] s’accordent pour dire qu’en ce milieu «le problème, ce sont les enseignants, et non les filles!». En effet, l’observation des pratiques enseignantes durant les cours de mathématiques révèle des attitudes négatives et de faibles attentes envers les filles (O’Conner, 2001). Ce sont ces attitudes négatives qui alimentent selon Lafontaine et Monseur (2009) «la confiance des garçons dans leurs capacités en mathématiques et sapent la confiance des filles, qui hésitent à s’engager dans des formations scientifiques» (p. 74). Par conséquent, nombreux sont les travaux qui posent que les filles développent en moyenne un niveau de sentiment d’efficacité personnelle moindre à l’égard des mathématiques que les garçons (Bergeron, 2016; Blanchard, 2010; Lent, 2008; Vouillot, 2012b). Dans le cadre du Programme international pour le suivi des acquis des élèves (PISA) élaboré par l’Organisation de coopération et de développement économique (OCDE, 2014), il a par exemple été noté que même quand les filles font jeu égal avec les garçons en mathématiques,

elles ont tendance à se dire moins persévérantes, moins ouvertes à la résolution de problèmes et moins animées par une motivation intrinsèque et instrumentale à l’idée d’apprendre les mathématiques, et à se dire plus anxieuses en mathématiques que les garçons.

OCDE, 2014, p. 18

Or, il a maintes fois été prouvé que le sentiment d’efficacité personnelle en mathématiques joue un rôle déterminant dans les choix d’orientation scolaire des élèves vers ce domaine (Galand et Vanlede, 2004; Gueudet, Khalloufi et Marc 2012; Lecomte, 2004; Lent, 2008). Et comme le suggèrent les travaux (théoriques) de Bandura (1986), la persuasion verbale est une source à partir de laquelle les enseignant·e·s de mathématiques peuvent influer positivement sur le sentiment d’efficacité personnelle des filles en mathématiques. Dès lors, étudier l’influence des enseignant·e·s de mathématiques dans l’orientation des filles vers cette voie à partir des mécanismes de persuasion verbale agissant sur le sentiment d’efficacité personnelle en mathématiques est une piste de recherche intéressante, et notamment dans le contexte camerounais où les filles demeurent sous-représentées en apprentissage et même en enseignement des mathématiques (MINESUP, 2015). Ainsi, la principale question à laquelle la présente recherche se propose de répondre est la suivante: comment les enseignant·e·s de mathématiques peuvent-elles et peuvent-ils influencer positivement le sentiment d’efficacité personnelle et le choix d’orientation des filles en mathématiques? En d’autres termes, par quel mécanisme, les enseignant·e·s de mathématiques peuvent-ils contribuer à développer le sentiment d’efficacité personnelle d’une part et à favoriser chez les filles le choix d’orientation en mathématiques d’autre part?

3. Cadre théorique

Inscrite dans le champ de la psychologie de l’éducation, cette étude, du point de vue théorique, prend appui sur la littérature relative aux comportements et attitudes des enseignant·e·s de mathématiques en contexte scolaire d’une part, et d’autre part à l’apport du sentiment d’efficacité personnelle dans la compréhension du choix mitigé des filles pour les mathématiques et des interventions visant à le rehausser.

3.1 Sentiment d’efficacité personnelle et orientation des filles en mathématiques

Encore appelé efficacité personnelle perçue, sentiment de compétence, auto-efficacité ou encore efficacité perçue, le sentiment d’efficacité personnelle est défini par Galand et Vanlede (2004) comme «le jugement que porte une personne sur sa capacité d’organiser et d’utiliser les différentes activités inhérentes à la réalisation d’une tâche à exécuter» (p. 4). Pour Lent (2008), ce sont «les jugements que les personnes portent sur leurs propres capacités d’organisation et de réalisation des activités qui permettent d’atteindre des types de résultats déterminés» (p. 3). C’est-à-dire, les croyances qu’a une personne sur sa capacité à mobiliser des connaissances et des actions pour réaliser une tâche spécifique. Ce concept s’inscrit dans le cadre de la théorie sociale cognitive de Bandura (1986) qui décrit les conduites des personnes comme étant le produit d’interactions entre: les facteurs internes (les croyances, les pensées, les attentes…), l’environnement et les comportements. Ici, les individus et leurs environnements s’influencent mutuellement. Pour Bandura (1986), une personne mobilise plus ou moins facilement un comportement en fonction de ses attentes et des images de soi, situant ainsi le sentiment d’efficacité personnelle.

Dès lors, la compréhension des choix d’orientation effectués par les élèves à l’école réside notamment dans l’analyse de leur sentiment d’efficacité personnelle. Dans le cadre plus général de la théorie sociale cognitive, ce concept a favorisé l’élaboration de la théorie sociale cognitive de l’orientation scolaire et professionnelle (TSCOSP) par les psychologues américains Lent, Brown et Hackett (2000). Dans cette perspective, de nombreux auteurs soulignent le rôle déterminant du sentiment d’efficacité personnelle dans les choix d’orientation (Blanchard, 2010; Bergeron, 2016; Galand et Vanlede, 2004; Lent, 2008). À titre illustratif, Galand et Vanlede (2004) affirment que le sentiment d’efficacité prédit «en partie les résultats scolaires, les choix de filière d’étude et les choix professionnels, même quand on tient compte des résultats antérieurs ou des capacités cognitives mesurées au moyen d’un test standardisé» (p. 5). Selon Stevanovic et Mosconi (2007), de nombreuses études portant sur le choix du futur métier des adolescent·e·s soulignent aujourd’hui l’importance du sentiment d’efficacité personnelle. Pour Blanchard (2010) en effet, les premières applications de la théorie des sentiments de compétence au domaine de l’orientation scolaire et professionnelle ont concerné la question de l’orientation des femmes dans les séries scientifiques. Il a d’ailleurs été relevé que les filles ont dans la plupart des cas un niveau de sentiment d’efficacité personnelle inférieur à celui des garçons en mathématiques (Bergeron, 2016; Blanchard, 2010; Lent, 2008; OCDE, 2014; Vouillot, 2012b).

Sur cette question, Gueudet, Khaloufi et Marc (2012) se prononcent en affirmant que la sous-représentation des filles en mathématiques par rapport aux garçons peut résulter d’une autocensure. Par autocensure, les filles, pour diverses raisons, pensent que les mathématiques ne sont pas faites pour elles, qu’elles ne peuvent pas atteindre leur objectif et renoncent dès lors à leur projet de poursuivre leurs études dans les mathématiques (Vouillot, 2012b). C’est-à-dire que les filles ne croient pas souvent en leur potentiel de réussite en mathématiques.

Face à cette situation, Marro et Vouillot (2004) pensent que c’est en parvenant à développer les sentiments d’efficacité que l’on pourra contribuer à diversifier les choix d’orientation qui demeurent actuellement très sexués. Pour opérationnaliser cette démarche, Blanchard (2010) souligne que, si l’on cherche à renforcer le sentiment de compétence des personnes engagées dans une démarche d’orientation, l’analyse de ses sources suggère des pistes d’intervention. La référence à ces sources (expériences actives de maîtrise, les expériences vicariantes, la persuasion verbale, l’état physiologique de l’individu) permet de mieux percevoir de quelle manière l’enseignant·e de mathématiques peut jouer un rôle déterminant dans l’orientation des filles en mathématiques.

3.2 Contribution des enseignant·e·s de mathématiques à la construction du sentiment d’efficacité personnelle des filles

Comme le relève Blanchard (2010), la persuasion verbale peut amener une personne à croire qu’elle peut réussir dans des tâches où elle a préalablement échoué (Blanchard, 2010). Ainsi, on peut tirer parti du soutien social et utiliser la persuasion afin d’encourager les étudiant·e·s à s’engager dans de nouvelles tâches, à persister en dépit de résultats initiaux négatifs et à les interpréter de façon positive (Lent, 2008). À ce sujet, Masson (2011) souligne qu’«on retrouve là l’aptitude que le pédagogue devra encourager, montrant ainsi que l’élève possède les capacités de réussir» (p. 36). L’enseignant·e de mathématiques se trouve alors interpellé à plus d’un titre dans la construction du sentiment d’efficacité personnelle des filles en mathématiques, vue que «les mathématiques s’étudient principalement dans les salles de classe, les ateliers et les laboratoires en présence de l’enseignant» (Ivowi, 2001, p. 1). Pour renchérir sur ce point de vue, Costes et al. (2008) précisent que même si d’autres facteurs peuvent intervenir en dehors de la classe, les professeurs de mathématiques et de physique ne doivent pas sous-estimer leur influence. En effet,

[l]’encouragement des élèves filles, la valorisation de leurs capacités (à résoudre, à démontrer, à manipuler, à comprendre, à exposer), les discussions scientifiques avec elles sont indispensables. Le rôle de l’enseignant·e est aussi de déjouer les stéréotypes encore trop souvent véhiculés par les manuels scolaires ou le matériel pédagogique. La présentation de la filière S et des options mathématiques, physique, chimie ou sciences et techniques de l’ingénieur, doit convaincre les filles que féminité et sciences ou technologie ne sont pas incompatibles, qu’elles y ont toute leur place, qu’elles peuvent y réussir au même titre que leurs camarades garçons.

Costes et al., 2008, p. 6-7

Dans la même veine, Morin-Messabel (2014) affirme que l’enseignant·e de mathématiques peut explicitement dire que les disciplines scolaires «n’ont pas de sexe», ce qui constitue une source d’information concernant la façon dont les élèves pourraient réussir. L’objectif étant selon Costes et al. (2008) que l’enseignant·e de mathématiques puisse pleinement remplir l’un de ses rôles, à savoir éclairer précisément le choix des filles en leur fournissant des éléments de réflexion sur leur situation, en particulier sexuée.

Au regard de ce qui précède, il apparaît bien clairement que les enseignant·e·s de mathématiques peuvent influencer positivement l’orientation des filles vers les mathématiques à travers les principaux mécanismes de persuasion verbale que sont: l’information, la motivation, le conseil et l’encouragement des filles afin qu’elles s’intéressent davantage aux mathématiques (Costes et al., 2008; Ivoui, 2001; Lent, 2008). Précisément, il s’agit comme le suggèrent les auteurs de la sensibilisation sur l’importance des mathématiques mais aussi de la motivation et des encouragements en vue de les inciter à s’orienter vers les séries scientifiques présentant plus de débouchés que les séries littéraires (Chazal et Guimond, 2003). D’ailleurs, un rapport de l’Examen national 2015 de l’Éducation pour tous précise que le Cameroun s’est engagé à éliminer les disparités de genre dans l’éducation des filles avec notamment « l’encouragement de ces dernières à » s’inscrire dans des filières scientifiques et technologiques.

Cependant, les données de recherches montrent que le bilan est mitigé quant à l’utilisation par les enseignant·e·s de mathématiques de ces mécanismes de persuasion verbale. De même, la situation camerounaise a été peu étudiée. En effet, une littérature abondante incrimine ces enseignant·e·s des comportements discriminatoires en défaveur des filles et en faveur des garçons durant les cours de mathématiques. O’Conner (2011) relève par exemple les mécanismes à partir desquels les enseignant·e·s de mathématiques rendent les études des filles difficiles. Parmi ces facteurs que l’on retrouve également chez plusieurs autres auteurs, nous pouvons citer les attitudes négatives et de faibles attentes concernant les résultats des filles (Gastineau et Ravaozanany, 2011; Morin-Messabel, Ferrière et Salle, 2012), la dynamique dans la salle de classe et des comportements discriminatoires en faveur des garçons (Bouya, 1993; Duru-Bellat, 1995, 2004; Lafontaine et Monseur, 2009; Mosconi, 2004). À titre d’exemple, Gastineau et Ravaozanany (2011) relèvent que, dans de nombreuses sociétés, les enseignant·e·s pensent que les filles seraient sages en classe, les garçons dissipés; les filles seraient plus douées pour les matières littéraires, les garçons pour les mathématiques. De plus, les travaux de Duru‑Bellat (2004) ont montré que depuis le primaire on observe au quotidien que les enseignant·e·s interagissent significativement plus avec les garçons qu’avec les filles et leur consacrent plus de temps. Il y aurait également moins d’encouragements, moins de remarques d’ordre cognitif et moins de questions ouvertes adressées aux filles.

4. Méthode

Face à la question de recherche qui se pose dans ce travail, nous faisons l’hypothèse qu’un niveau élevé d’influence des enseignant·e·s de mathématiques sur les quatre mécanismes de persuasion verbale contribue à augmenter le niveau de sentiment d’efficacité personnelle en mathématiques et à favoriser le choix d’orientation des filles pour ce domaine. Autrement dit, les filles qui sont à la fois informées, motivées, conseillées et encouragées par leur enseignant·e de mathématiques sont plus enclines à avoir un niveau de sentiment d’efficacité personnelle élevé en mathématiques et à choisir une orientation vers ce domaine par rapport à celles qui l’ont moins été relativement à ces quatre dimensions.

4.1 Participantes

Sur un total de 269 filles que compte le lycée d’enseignement général de Ngoa-Ékélé à Yaoundé en 2017 dans l’ensemble des classes de troisième (allemand et espagnol), 150 ont marqué volontairement leur accord pour participer à l’étude. Leur âge est compris entre 11 et 21 ans (moyenne = 15 ans et 1 mois, écart type = 1 an et 5 mois).

4.2 Instrument de mesure

Les principales variables mesurées dans cette étude concernent le niveau d’influence des enseignant·e·s de mathématiques dans l’orientation des filles, le sentiment d’efficacité personnelle et le choix de série opéré par les filles. Pour ce faire, une enquête par questionnaire a été effectuée.

Comme nous l’avons relevé au niveau du cadre théorique, le niveau d’influence des enseignant·e·s de mathématiques dans l’orientation des filles est apprécié à l’aune des quatre principaux mécanismes de persuasion verbale consistant à informer, motiver, conseiller et encourager les filles afin qu’elles s’intéressent davantage aux mathématiques. Ainsi, les quatre principales questions fermées suivantes ont été posées:

  • Ton prof de maths, a-t-il déjà eu à te parler de l’importance des maths?

  • Ton prof de maths, te motive-t-il parfois à ce que tu t’intéresses bien aux mathématiques?

  • Ton prof de maths, t’a-t-il déjà conseillée de t’orienter vers la seconde C?

  • Ton prof de maths, t’a-t-il déjà encouragée pour que tu fasses la seconde C?

Par ailleurs, deux autres questions ont aussi été posées pour savoir si dans une certaine mesure les enseignant·e·s de mathématiques pouvaient constituer un problème pour les filles (« Les profs de maths te donnent-ils parfois l’impression que les mathématiques sont plus faites pour les garçons? »,« Ton prof de maths fait-il parfois à ce que tu aies peur des mathématiques? ») comme le soulignent certains travaux (Bouya, 1993; O’Conner, 2011). Une telle mesure permettrait de neutraliser cette variable afin d’avoir une idée plus claire sur les résultats de l’étude.

Le niveau du sentiment d’efficacité personnelle en mathématiques est mesuré à partir de l’échelle tirée des travaux de Bergeron (2016). C’est un questionnaire autorapporté comportant sept items où les élèves doivent indiquer leur degré d’accord sur l’échelle de Likert à cinq points allant de 1 (fortement en désaccord) à 5 (fortement en accord). Celle-ci présente une consistance interne acceptable (α = 0,71).

À la fin du questionnaire, une question a été posée pour relever le choix de chaque fille entre la seconde C dominée par les mathématiques et la seconde A qui est la voie littéraire. Précisons que les filles remplissaient le questionnaire vers la fin de l’année scolaire, au moment où elles avaient déjà effectué les choix de série auprès des conseillères et conseillers d’orientation.

4.3 Procédure

L’étude s’est déroulée en deux jours, du lundi 27 au mardi 28 mars 2017, dans l’enceinte du lycée de Ngoa-Ékélé. Après avoir formulé notre demande d’enquête auprès du responsable d’établissement quelques mois avant, nous avons été admis dans les salles de classe. Après notre présentation, nous avons dit aux élèves que nous aimerions avoir quelques minutes avec eux pour remplir un questionnaire relatif à l’apprentissage des mathématiques d’une façon générale. Nous avons indiqué que la participation à cette étude est facultative et ne concerne que les filles.

Une fois le questionnaire distribué, nous avons attiré l’attention des filles sur le fait qu’elles étaient tenues de bien lire l’en-tête avec les consignes mentionnées avant de commencer à répondre au questionnaire. De plus, il leur était rappelé que les réponses étaient personnelles (pour éviter la communication avec la voisine). Elles ont directement répondu par écrit aux questions posées. Dans l’ensemble, les filles ont mis en moyenne 10 minutes pour remplir le questionnaire et n’éprouvaient pas de difficultés de compréhension. Seules celles qui avaient marqué leur accord et leur consentement pour participer à l’étude recevaient le questionnaire pour y répondre.

4.4 Méthode d’analyse des données

Au cours des analyses, la variable se rapportant au niveau d’influence des enseignant·e·s de mathématiques est opérationnalisée selon trois modalités à savoir, un faible niveau, un niveau moyen et un niveau élevé d’influence. En référence aux quatre questions posées à ce sujet, le niveau d’influence est considéré comme étant faible si les deux dimensions suivantes sont retenues: soit aucune des quatre questions n’a obtenu de réponse par l’affirmative ou qu’une seule en a obtenu une. Pour le niveau moyen, une dimension est considérée, notamment le fait de répondre par l’affirmative à deux des quatre questions posées. Le niveau élevé considère deux dimensions, notamment le fait de répondre par l’affirmative à trois ou aux quatre questions posées. Les deux autres questions sur les problèmes éventuels causés par les enseignant·e·s de mathématiques dans les études des filles sont exploitées au niveau de la discussion pour des raisons de prudence dans l’interprétation et la compréhension des résultats obtenus. Dès lors, pour étudier l’effet du niveau d’influence des enseignant·e·s de mathématiques sur le choix de série, une régression logistique binaire est effectuée. Par ailleurs, le niveau du sentiment d’efficacité personnelle étant de nature quantitative, une analyse de la variance à un facteur associant le test de Duncan est appliquée pour étudier l’effet du niveau d’influence de ces enseignant·e·s sur le sentiment d’efficacité personnelle des filles en mathématiques. Au cours de cette démarche, le logiciel SPSS (Statistical Package for Social Sciences), version 21.0, est celui que nous avons utilisé.

5. Résultats

La validation de l’hypothèse préalablement formulée nécessite deux niveaux d’analyse à savoir d’une part, l’effet du niveau d’influence des enseignant·e·s de mathématiques sur le sentiment d’efficacité personnelle des filles en mathématiques et d’autre part, le lien entre ce niveau d’influence et le choix de série opéré par les filles.

5.1 Niveau d’influence des enseignant·e·s de mathématiques dans l’orientation des filles vers les mathématiques et sentiment d’efficacité personnelle

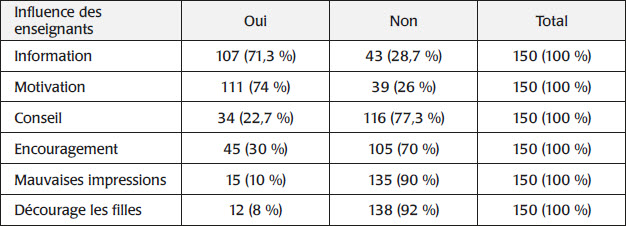
Les analyses préliminaires telles que présentées au tableau 1 font ressortir sur chacune des quatre questions mesurant l’influence des enseignants·e·s de mathématiques le pourcentage des réponses affirmatives données par les filles.

Tableau 1

Influence des enseignant·e·s de mathématiques pour chacune des questions posées au sujet de l’orientation des filles vers les mathématiques

Influence des enseignant·e·s de mathématiques pour chacune des questions posées au sujet de l’orientation des filles vers les mathématiques

-> See the list of tables

Ce tableau indique que les enseignant·e·s de mathématiques sont dans l’ensemble plus enclin·e·s à informer les filles sur l’importance des mathématiques et à les motiver pour qu’elles s’intéressent à cette discipline, mais, conseillent et encouragent difficilement ces dernières pour qu’elles s’orientent en ce domaine. Ainsi, le niveau d’influence de ces enseignant·e·s est dans l’ensemble moyen comme nous le précise le tableau 2

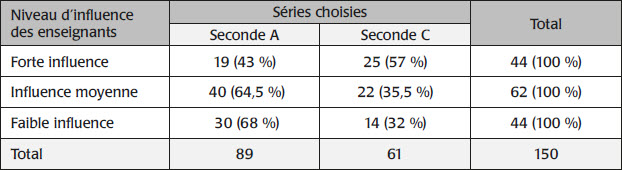
Tableau 2

Niveau d’influence des enseignant·e·s de mathématiques dans l’orientation des filles vers les mathématiques

Niveau d’influence des enseignant·e·s de mathématiques dans l’orientation des filles vers les mathématiques

-> See the list of tables

Au regard de ce tableau, on constate que les filles sont plus susceptibles de connaître une influence de niveau moyen (41,4 %) de la part de l’enseignant·e de mathématiques au cours de leurs études en mathématiques. Dans cet ordre d’idées, l’analyse de la variance (à un facteur) montre que le niveau d’influence de l’enseignant·e de mathématiques dans l’orientation des filles détermine significativement mais de manière modeste, le sentiment d’efficacité personnelle en mathématiques (F(2, 150) = 3,43, p = 0,035, η2 = 0,04). En effet, le test de Duncan confirme que les filles chez qui le niveau d’influence est fort s’estiment plus compétentes en mathématiques (M = 3,64, ET = 0,75) que celles chez qui cette influence est moyenne (M = 3,28, ET = 0,79) et faible (M = 3,21, ET = 0,97). Aucune différence n’est par conséquent observée entre le sentiment d’efficacité personnelle des filles de niveau d’influence moyenne et celui des filles de niveau d’influence faible.

5.2 Niveau d’influence des enseignant·e·s de mathématiques et choix de série opéré par les filles

Les analyses préliminaires à ce sujet révèlent que, sur les 150 filles interrogées, 89 ont choisi de s’orienter en seconde A (59,3 %) contre 61 (40,7 %) qui ont opté pour la seconde C. Ainsi, les proportions diffèrent significativement, étant donné que ces filles choisissent plus la seconde A que la seconde C (χ2(1, 150) = 5,23, p < ,05). Dans le même ordre d’idées, on note que celles qui ont choisi la seconde C (3,97) ont un sentiment d’efficacité personnelle en mathématique significativement (t(150) = 8,95, p = 00, η2 = 0,35) supérieur à celui des filles ayant choisi la seconde A (2,95). Ces choix ont ensuite été étudiés en fonction du niveau d’influence des enseignant·e·s de mathématiques. Le tableau 3 présente les données y relatives.

Tableau 3

Influence des enseignant·e·s de mathématiques dans l’orientation des filles et choix de série

Influence des enseignant·e·s de mathématiques dans l’orientation des filles et choix de série

-> See the list of tables

Sur les 44 filles chez qui l’influence des enseignant·e·s de mathématiques est forte, 25 ont choisi la seconde C tandis que 19 ont choisi la seconde A. En revanche, sur les 44 filles chez qui cette influence est faible, seules 12 ont choisi la seconde C lorsque 30 ont plutôt opté pour la seconde A. Lorsque cette influence est moyenne, les filles choisissent moins la seconde C (35,5 %) que la seconde A (64,5 %). Ainsi, quand l’influence des enseignant·e·s de mathématiques est faible ou moyenne, les filles ont plus tendance à choisir la voie littéraire que la voie des mathématiques. En revanche, elles choisissent plus la voie des mathématiques (57 %) par rapport à la voie littéraire (43 %) lorsque cette influence est forte. La figure 1 illustre mieux ces tendances.

Figure 1

Choix des filles en fonction du niveau d’implication des enseignant·e·s de mathématiques

Choix des filles en fonction du niveau d’implication des enseignant·e·s de mathématiques

-> See the list of figures

De ce fait, les analyses indiquent que le niveau d’influence des enseignant·e·s de mathématiques dans l’orientation des filles a un effet significatif sur le choix de série opéré entre la seconde A et la seconde C. En effet, le niveau d’influence des enseignant·e·s de mathématiques dans l’orientation des filles explique en partie le choix de série opéré par ces dernières avec une variance de l’ordre de 6 %. Précisément, le modèle démontre que les filles chez qui l’influence des enseignants de mathématiques est faible (B = 1,037, p = 0,02) et celles chez qui l’influence des enseignants de mathématiques est moyenne (B = 0,872, p = 0,03) ont respectivement 3 (Exp(B) = 2,82) et 2 (Exp(B) = 2,39) fois plus de chance environ de choisir la seconde A que la seconde C par rapport à celles chez qui l’influence des enseignant·e·s de mathématiques est forte. Ce qui revient à dire qu’un fort niveau d’influence des enseignant·e·s de mathématiques dans l’orientation des filles est l’une des variables associées significativement au choix de la voie des mathématiques.

6. Discussion

En complément aux études antérieures (Bouya, 1993; Costes et al., 2008; Ivoui, 2001; Monseur, 2009; O’Conner, 2001), la démarche entreprise dans ce travail s’est proposée d’étudier de façon empirique les mécanismes à partir desquels les enseignant·e·s de mathématiques peuvent influencer l’orientation des filles de façon à réduire considérablement les disparités de genre qui perdurent en mathématiques. L’hypothèse préalablement formulée a été intégralement confirmée. C’est dire qu’une forte influence des enseignant·e·s de mathématiques sur les quatre mécanismes de persuasion verbale que sont l’information, la motivation, le conseil et l’encouragement, contribue à augmenter le niveau du sentiment d’efficacité personnelle en mathématiques et à favoriser le choix d’orientation des filles pour ce domaine. Cependant, ces résultats restent discutables sur quelques points.

6.1 L’implication des enseignant·e·s de mathématiques au regard des données relatives au contexte scolaire

De prime abord, les résultats révèlent un nombre moins important de filles chez qui l’influence des enseignant·e·s de mathématiques est forte. Autrement dit, que les enseignant·e·s ne semblent pas aider suffisamment les filles à s’orienter vers la voie des mathématiques. Lorsqu’elles et ils décident de le faire, elles et ils insistent plus souvent sur deux dimensions en informant parfois les filles de l’importance des mathématiques et en les motivant aussi afin qu’elles s’intéressent aux mathématiques (tableau 1). Elles et ils ne conseillent et n’encouragent pas assez les filles vers la voie des mathématiques. Pourtant, Coste et al. (2008) et O’Conner (2011) soulignent l’importance de l’encouragement des élèves filles et des conseils afin de les aider à mieux s’intéresser aux mathématiques. Par conséquent, on observe un nombre important de filles qui ont déclaré n’avoir pas été véritablement assistées par leurs enseignant·e·s de mathématiques en ce qui a trait aux quatre mécanismes de persuasion verbale. À ce sujet, on ne saurait parler de discrimination étant donné que l’avis des garçons n’a pas été pris en compte. Toutefois, la prudence commande de ne pas complètement occulter cette piste des arguments développés dans cette étude. En effet, nous avons relevé l’avis de filles qui confirment que les enseignant·e·s de mathématiques leur donnent parfois l’impression que les mathématiques sont faites pour les garçons (15 exactement, tableau 1). À cet effet, Schreiber et Toma (2006) soulignent qu’il y aurait une discrimination passive qui se manifeste lorsqu’un·e enseignant·e ne dit pas à une fille d’aller vers les mathématiques en donnant comme argument qu’il faut respecter le choix des élèves, mais encourage incidemment un garçon vers cette voie. Duru-Bellat (2004) avait d’ailleurs mentionné que durant les cours de mathématiques les filles reçoivent moins d’encouragements. Dans la même veine, Pretto et Regner (2014) posent que les femmes semblent faire l’objet d’une discrimination systématique dans ce domaine scientifique, fondée sur des préjugés, des stéréotypes, des mythes et des croyances. Par ailleurs, nous relevons quelques cas de filles qui déclarent que les enseignants de mathématiques leur font parfois peur en mathématiques (12 filles précisément, tableau 1). Sur cette question, Bouya (1993) affirme que:

L’enseignement des mathématiques en Afrique francophone est entouré d’un certain voile mythique relatif à la difficulté de cette discipline; l’enseignant, particulièrement en mathématiques, «terrorise» les élèves. Pareilles attitudes découragent complètement les meilleures volontés et la motivation déjà faible des filles.

p. 20

Ainsi, il semble illusoire de penser que ce sont les mathématiques elles-mêmes qui suscitent une attitude négative de la part des filles (Pretto et Regnier, 2014). Ces représentations se forment précisément dans le cadre scolaire, sous l’influence de l’enseignant·e, d’autant plus que les mathématiques s’étudient principalement dans les salles de classe, en présence de cette dernière ou ce dernier (Ivowi, 2001). Nos résultats s’inscrivent ainsi dans la logique des analyses de Mariotti (2002) qui souligne que «l’un des supports de construction de ces représentations peut se trouver dans les divers guides mis à disposition des élèves à partir de la classe de troisième et relayés oralement par les professeurs» (p. 4) et de Morin-Messabel et al. (2012) qui précisent que les travaux relatifs au contexte scolaire montrent essentiellement en quoi les stéréotypes de sexe marquent les interactions dans le groupe-classe, en lien avec l’enseignant·e de mathématiques. Or, il a été montré dans le cadre de la théorie de la menace du stéréotype (Steele et Aronson, 1995) que la simple présence du stéréotype à l’école peut aider à expliquer pourquoi il y a moins de femmes que d’hommes qui poursuivent des carrières scientifiques et qui y réussissent (Désert, 2004; Régner, Steele, Ambady, Thinus-Blanc et Huguet, 2014; Toczek, 2005). Dans cette lancée, Plante et al. (2010) soulignent qu’en dépit des stéréotypes explicites promasculins moins saillants qu’auparavant en mathématiques, les élèves entretiennent toujours implicitement ces croyances. C’est dire que l’école, tant du point de vue de la socialisation que de la transmission des savoirs, tend à reproduire les rapports sociaux de sexe comme rapports inégaux entre les filles et les garçons (Toczek, 2005).

Dans ce contexte, les enseignant·e·s de mathématiques devraient être fortement impliqué·e·s dans l’orientation des filles en leur servant de contre-stéréotypes (Devif, Reeb, Morin-Messabel et Kalampalikis, 2018) afin de mieux déjouer les stéréotypes de genre qui pèsent sur elles. Pour Costes et al. (2008), les professeur·e·s de mathématiques n’ont pas à sous-estimer leur influence, car le fait d’avoir bénéficié ou non de leurs conseils semble exercer une influence positive chez les filles. Dans cette optique, les résultats ont montré que les filles chez qui l’implication de l’enseignant·e de mathématiques est forte ont un sentiment d’efficacité personnelle plus élevé et choisissent de préférence la voie des mathématiques.

6.2 Implication des enseignant·e·s de mathématiques, sentiment d’efficacité personnelle et orientation des filles en mathématiques

Les résultats de l’étude indiquent par ailleurs que les filles qui ont choisi la seconde C ont un sentiment d’efficacité personnelle élevé en mathématiques (3,97) par rapport à celles qui ont opté pour la seconde A (2,95). Ainsi, l’étude corrobore les travaux qui s’inscrivent dans la perspective de la théorie sociale cognitive de l’orientation scolaire et professionnelle, et qui soulignent que le sentiment d’efficacité personnelle en mathématiques reste un bon prédicteur dans le choix d’études en mathématiques (Bergeron, 2016; Blanchard, 2010; Lent, 2008; Vouillot, 2012b). Le sentiment d’efficacité personnelle en mathématiques permet dès lors de comprendre pourquoi les filles ont plus tendance à éviter la voie des mathématiques. On note à cet effet que le niveau du sentiment d’efficacité personnelle des filles en mathématiques fluctue selon que le niveau d’influence des enseignant·e·s est fort, moyen ou faible. Il est donc possible pour les enseignant·e·s de mathématiques d’agir sur le sentiment d’efficacité personnelle des filles en mathématiques afin de les aider à investir davantage ce domaine. C’est ce qui ressort également dans la littérature chez certains auteurs.

En effet, Bergeron (2016) dans ses travaux insiste sur le soutien des enseignant·e·s en soulignant que les femmes en mathématiques expliquent en grande partie leur choix de carrière par les interactions enrichissantes avec leurs enseignant·e·s de mathématiques. Selon elle, ce «soutien peut prendre la forme de simples encouragements verbaux, de tutorat privé, de séances de reformulation en classe, de rétroaction personnalisée ou de récompenses» (Bergeron, 2016, p. 66). Dans le même ordre d’idées, Lent (2008) suggère que les efforts pour modifier les sentiments d’efficacité personnelle des filles en mathématiques peuvent bénéficier de la mise en oeuvre de procédures de restructuration cognitive qui les encouragent à produire des attributions de réussite qui renforcent le soi. Pour ce faire, Blanchard (2010) précise que la persuasion verbale peut amener une personne à croire qu’elle peut réussir dans des tâches où elle a préalablement échoué. C’est dire qu’on peut effectivement tirer parti du soutien social de l’enseignant·e et utiliser la persuasion afin d’encourager les filles à mieux s’engager vers les études en mathématiques. Dans cette démarche, Lent (2008) avance l’âge au cours duquel cette intervention peut être principalement fructueuse, en ces termes:

Les interventions éducatives qui visent à augmenter les sentiments d’efficacité et les attentes de résultats favorables sont probablement plus utiles au cours de l’enfance et de l’adolescence, avant que les intérêts et les aspirations deviennent plus stables et que certains types de choix soient prématurément écartés.

p. 12

Ce qui revient à dire que c’est en parvenant à développer le sentiment d’efficacité chez les adolescent·e·s précisément que l’on pourra contribuer à diversifier les choix d’orientation qui demeurent actuellement très sexués (Marro et Vouillot, 2004). Dès lors, les disparités de genre observées dans l’orientation en mathématiques perdurent, parce que les filles dans leur immense majorité sont moins enclines à croire en leur potentiel et n’osent pas emprunter cette voie déjà stéréotypée où l’échec aurait un coût cognitif, affectif et social élevé (Gianettoni, Simon-Vermot et Gauthier, 2010). Or, en influant fortement dans l’orientation des filles depuis les classes de troisième où elles sont encore des adolescentes, les enseignant·e·s de mathématiques pourraient efficacement les inciter à s’orienter davantage vers les mathématiques à partir du développement de leur sentiment d’efficacité personnelle, notamment en multipliant les occasions où les filles ont des expériences actives de maîtrise. Il serait question pour les enseignant·e·s de mathématiques par exemple d’assister ces filles dans la résolution des exercices et des problèmes mathématiques durant leurs études et de leur apporter le soutien nécessaire pour surmonter les obstacles éventuels auxquels elles peuvent être confrontées.

7. Conclusion

Au regard des analyses faites dans ce travail, il est judicieux de reconnaître les limites que présente l’étude. En effet, il y a des filles qui ont reçu une faible assistance des enseignant·e·s de mathématiques, mais qui ont eu un sentiment d’efficacité personnelle élevé et ont choisi la seconde C. De même, il y en a qui ont reçu une forte assistance, mais qui malgré tout ont opéré le choix de la seconde A. Nous avons d’ailleurs trouvé que le niveau d’influence des enseignant·e·s de mathématiques n’explique qu’une faible partie de la variance du choix de série opéré par les filles. Il importe de noter à ce sujet que les personnes enseignantes peuvent considérer que l’orientation n’est pas dans leur mandat, raison pour laquelle ils ne conseillent ni n’encouragent les filles vers la seconde C. Dès lors, elles exercent une influence au mieux moyenne, mais moins susceptible de conduire ces filles vers la voie des mathématiques. Ce qui laisse donc envisager qu’il y aurait d’autres sources d’influence dans l’orientation des filles vers les mathématiques qui ne se limitent pas à l’école. En effet, nous ne saurions occulter le rôle que joue par exemple la famille dans l’orientation. Il est d’ailleurs admis que le choix de filière d’un élève peut être contraint par des pressions familiales (Mosconi, 2004). En ce sens, une fille peut être motivée et encouragée vers les mathématiques par son enseignant·e de mathématiques, mais, être contrainte par ses parents ou son environnement familial à choisir une seconde A. De même, l’intérêt et le niveau de l’élève en mathématiques pourraient conditionner le choix d’orientation. Une autre étude pourrait en conséquence être menée en procédant à une analyse conjointe de l’influence des enseignant·e·s de mathématiques et de la famille dans l’orientation des élèves des deux sexes vers les mathématiques tout en contrôlant le niveau de l’élève. Cette perspective aurait alors pour but d’évaluer le poids de chacun de ces acteurs dans le choix des filières par les filles et les garçons.

Par ailleurs, il aurait été intéressant d’inclure à la fois les filles et les garçons dans cette étude. Ce qui aurait permis d’une part, d’affiner les analyses précisément au sujet des comportements discriminatoires des enseignant·e·s dans la compréhension des disparités de genre en mathématiques, et de l’autre, de comprendre si faute d’accorder une assistance particulière aux filles, ce sont plutôt les garçons qui bénéficient de cette attention. De même, le caractère exploratoire de la présente recherche suggère de s’interroger sur la réplicabilité de ses résultats au regard de la démarche adoptée pour la mesure de l’influence des enseignant·e·s de mathématiques. En effet, le nombre de questions qui déterminent cette influence n’est pas égal dans les catégories puisque nous nous appuyons sur les proportions auxquelles on devrait s’attendre dans chacun des niveaux si l’échantillon global suit une tendance normale. Dès lors, il serait important de répliquer cette étude dans d’autres contextes suivant cette méthode dans une future recherche pour davantage documenter la littérature sur la contribution des enseignant·e·s de mathématiques à la réduction des disparités de genre dans le domaine des mathématiques.

Proposer des voies et des moyens pour réduire les disparités de genre en mathématiques dans des démarches futures apparaît ainsi adéquat. Dans la présente étude, il a été noté que les enseignant·e·s de mathématiques influencent significativement le choix des filles pour les mathématiques. En référence aux travaux de Bagès et al. (2008) et Marx et Roman (2002), une étude où le sexe de l’enseignant·e serait pris en compte pourra être envisagée afin de voir si les filles et les garçons sont enclin·e·s à plus s’orienter vers les mathématiques lorsqu’ils et elles sont en présence de l’enseignant·e de même sexe. Cette considération permettrait davantage de comprendre les variables qui déterminent l’efficacité d’un modèle contre-stéréotypique en mathématiques chez les filles. Par ailleurs, comme le suggèrent de nombreux travaux (Devif et al., 2018; Morin-Messabel et al., 2012), une meilleure formation au rôle de conseil et à l’éducation à l’égalité est nécessaire pour amener les enseignant·e·s à accomplir judicieusement leur tâche dans la démarche de l’orientation.