Abstracts
Résumé
La Fédération Wallonie-Bruxelles met à la disposition des enseignants des outils d’évaluation susceptibles de diagnostiquer la capacité des élèves à mobiliser et à combiner, en situation inédite, un ensemble de procédures apprises. Si plusieurs chercheurs se sont investis dans la réflexion scientifique autour de ces outils et de leur pouvoir diagnostique, la question de l’impact des contenus spécifiques évalués par ceux-ci est peu envisagée. En analysant un outil centré sur l’algèbre élémentaire, cet article a pour ambition de rendre compte de la plus-value apportée par un regard alimenté par les recherches menées dans la discipline ciblée. Dépassant les constats généraux posés par la passation de l’outil telle que prévue par les auteurs dans une logique de compétences, les résultats mettent en perspective les démarches mises en oeuvre par les élèves devant les différentes tâches proposées. Au-delà des constats spécifiques à la tâche analysée, cet article montre l’importance de regards croisés sur la question de l’évaluation des compétences.
Mots-clés :
- compétence,
- tâche complexe,
- algèbre,
- arithmétique,
- démarches de résolution
Abstract
The Wallonia-Brussels Federation offers teachers assessment tools meant to measure students’ abilities to select and combine, in unusual situations, learnt-in-class procedures. Even though many researchers were involved into scientific reflections on these tools and their diagnostic value, the impact of the contents specifically assessed has not been really considered. The purpose of this paper is to highlight the importance of this aspect through the analysis of a tool related to elementary algebra. While extending the general findings arising from the tool as intended by the authors in the competency-based approach, the results confront the strategies adopted by students when dealing with the different tasks proposed. Beside the specific results to tested task, the paper intends to show the added value of this integrated approach to the competence assessment issue.
Keywords:
- competence,
- complex task,
- algebra,
- arithmetic,
- problem-solving strategies
Resumo
A Federação Valónia-Bruxelas coloca à disposição dos professores instrumentos de avaliação sucetíveis de diagnosticar a capacidade dos alunos para mobilizar e combinar, em situação inédita, um conjunto de procedimentos aprendidos. Apesar da reflexão científica de muitos investigadores em torno destes instrumentos e do seu poder de diagnóstico, a questão do impacto dos conteúdos específicos avaliados tem sido pouco considerada. Analisando um instrumento centrado na álgebra elementar, este artigo tem como propósito dar conta da mais-valia que resulta de um olhar alimentado pelas investigações realizadas nesta disciplina em particular. Ultrapassando as constatações gerais colocadas pela aplicação do instrumento numa lógica de competências de acordo com a intenção dos autores, os resultados permitem perspetivar as estratégias adotadas pelos alunos perante as tarefas propostas. Para além das constatações específicas da tarefa analisada, este artigo mostra os olhares cruzados sobre a problemática da avaliação de competências.
Palavras chaves:
- competências,
- tarefa complexa,
- álgebra,
- aritmética,
- estratégias de resolução de problemas
Article body
Introduction
Depuis quelques années, le concept de compétence est au coeur de nombreux programmes d’études de plusieurs pays francophones (Eurydice, 2012). La Fédération Wallonie-Bruxelles s’est engagée dans cette voie dès la fin des années 1990. La compétence, définie dans les textes légaux comme « l’aptitude à mettre en oeuvre un ensemble organisé de savoirs, de savoir-faire et d’attitudes permettant d’accomplir un certain nombre de tâches » (Communauté française de Belgique, 1997, art. 5.1), présente l’intérêt de mettre l’accent sur le sens à donner aux apprentissages. Les enseignants attendent des élèves qu’ils puissent mobiliser leurs connaissances dans des contextes variés et devant des situations complexes et inédites (Beckers, 2012).
En vue d’aider les enseignants à concrétiser cette notion de compétence dans les différentes disciplines, des commissions ont élaboré des outils d’évaluation diagnostique susceptibles de cerner les capacités des élèves à mobiliser et à combiner un ensemble de procédures apprises en classe en vue de résoudre des tâches complexes. Pour les épreuves destinées aux élèves de 6 à 14 ans, les concepteurs se sont basés sur les principes d’un dispositif d’évaluation en trois phases proposé par Rey, Carette, Defrance et Kahn (2006).
Si plusieurs chercheurs se sont investis dans la réflexion scientifique autour de l’élaboration et de la validation de ce type d’épreuve d’évaluation de compétences (Carette, 2007 ; De Ketele & Gérard, 2005 ; Dierendonck & Fagnant, 2014 ; Lafontaine, 2012 ; Scallon, 2007), la question de l’impact des contenus spécifiques évalués par ce type d’épreuve est, à notre connaissance, plus rarement envisagée. Cet article vise à rendre compte de l’intérêt de croiser des apports de deux courants de recherche pour analyser un outil diagnostique mis à la disposition des enseignants : un regard issu de recherches portant sur l’évaluation de compétences qui envisagent une réflexion transdisciplinaire (la même logique étant appliquée aux différentes disciplines), voire interdisciplinaire (plusieurs exemples d’épreuves construites par Rey et ses collaborateurs [2006] ou inspirées de leur « modèle » évaluent conjointement des compétences en français et en mathématiques) et un regard disciplinaire appuyé sur les recherches menées en didactique sur le contenu même de l’outil.
Dans cette perspective, ce texte propose une réflexion autour de l’apport diagnostique d’un outil qui aborde une facette spécifique du champ algébrique envisagé comme « outil de résolution via la modélisation pour résoudre des problèmes “arithmétiques” formulés en langue naturelle sous forme d’équations » (Grugeon, Pilet, Chenevotot, & Delozanne, 2012). Une première analyse qualitative, centrée sur le contenu même de l’outil et sur les différentes questions qu’il soulève, comprendra un apport quantitatif, amené à la suite de la passation de l’outil dans huit écoles de 3e secondaire (grade 9, élèves de 14-15 ans).
Fondements théoriques
Dans cette partie, nous proposons de présenter puis de comparer quelques apports issus de deux courants de recherche : d’une part, ceux amorcés par Rey et ses collaborateurs (2006) portant sur l’évaluation des compétences et, d’autre part, quelques éléments issus de recherches en didactique portant sur la mise en équation de problèmes arithmétiques.
Quelques apports des recherches centrées sur l’évaluation des compétences
Les outils d’évaluation ont été conçus en référence au modèle d’évaluation en « phases » développé par Rey et ses collaborateurs (2006). Ces auteurs ont analysé les référentiels de compétences et ont mis en évidence que, dans la plupart de ceux-ci, trois degrés de compétences peuvent être ciblés.
Les compétences de premier degré (« compétences élémentaires », « procédures », « procédures élémentaires » ou « procédures automatisées ») : « Savoir exécuter une opération (ou une suite prédéterminée d’opérations) en réponse à un signal (qui peut être en classe une question, une consigne, ou une situation connue et identifiable sans difficulté, ni ambiguïté) » (Rey et al., 2006, p. 26).
Les compétences de deuxième degré (« compétences élémentaires avec cadrage ») : « Posséder toute une gamme de ces compétences élémentaires et savoir, dans une situation inédite, choisir celle qui convient » (Loc. cit.). Dans ce type de situation, une interprétation de la situation (ou un « cadrage » selon la terminologie des auteurs) est nécessaire. L’élève doit pouvoir déterminer quelle est la procédure qui convient, parmi l’ensemble de celles qu’il a apprises. Autrement dit, il doit mobiliser (et non simplement appliquer) la procédure adéquate.
Les compétences de troisième degré (« compétences complexes ») : « Savoir choisir et combiner plusieurs compétences élémentaires pour traiter une situation nouvelle et complexe » (Loc. cit.). Dans ce type de situation, une interprétation de la situation et une organisation de la démarche de résolution sont nécessaires. En effet, ces tâches évaluent « la capacité des élèves à choisir et à combiner, parmi les procédures qu’ils connaissent, plusieurs d’entre elles afin de résoudre adéquatement un problème nouveau pour eux » (Ibid., p. 44).
Ce ne serait qu’au troisième degré que l’on pourrait parler d’« authentiques compétences » nécessitant une mobilisation intégrée de différentes ressources pour accomplir une tâche (Rey et al., 2006). Ces auteurs pensent également que toute épreuve diagnostique de compétences devrait conduire à répondre aux trois questions suivantes : « (a) L’élève est-il capable de choisir et de combiner des procédures lors de la résolution de tâches complexes ? ; (b) L’élève est-il capable de choisir une bonne procédure lors de la résolution d’une tâche qui ne fait pas appel à la combinaison de plusieurs procédures ? ; (c) L’élève maîtrise-t-il les procédures nécessaires à la résolution de la tâche complexe ? » (Carette, 2007, p. 61).
En vue de répondre à ces questions, Rey et ses collaborateurs (2006 ; voir aussi Carette, 2007) ont dès lors développé une procédure d’évaluation en trois phases.
Lors de la phase 1, les élèves font face à « une tâche complexe exigeant le choix et la combinaison d’un nombre significatif de procédures que les élèves doivent posséder » (Rey et al., 2007, p. 92).
Lors de la phase 2, les élèves font face à « la même tâche complexe, mais découpée en tâches élémentaires, présentées dans l’ordre où elles doivent être accomplies pour réaliser la tâche globale. L’élève doit choisir, parmi les procédures qu’il connaît, celle qui convient à chacune des tâches élémentaires » (Loc. cit.).
Lors de la phase 3, « on demande aux élèves d’accomplir les procédures exigées dans les phases précédentes, mais sous une forme décontextualisée » (Loc. cit.).
Rey et ses collaborateurs ont étudié la question de la hiérarchie entre les trois phases de leurs outils. Ils aboutissent à la conclusion que les tâches qui mesurent les procédures sont les mieux réussies, alors que les tâches complexes non décomposées sont celles qui posent le plus de difficultés aux élèves (Carette, 2007 ; Rey et al., 2006). En accord avec ce constat et à l’instar de l’interprétation proposée par les auteurs, d’autres études ont également mis en évidence l’importance de la maîtrise et de l’automatisation des procédures dans le cadre de l’acquisition des compétences (Crahay & Detheux, 2005 ; Marcoux, 2012). Tous ces auteurs s’accordent sur le fait que la maîtrise de procédures automatisées (telles qu’elles sont évaluées dans la phase 3 du modèle) est une condition nécessaire, mais pas suffisante pour réussir des tâches impliquant la mobilisation de ces mêmes procédures en situation complexe.
Quelques apports des recherches centrées sur la mise en équation de problèmes
Deux éléments développés dans les recherches en didactique de l’algèbre élémentaire nous paraissent particulièrement intéressants à présenter ici. Ils concernent, d’une part, le choix même de la tâche complexe et, d’autre part, les enjeux cognitifs de la mise en équation de problèmes.
Le choix de la tâche complexe
Plusieurs auteurs (Duval, 1993, 2002 ; Filloy, Rojano, & Puig, 2008 ; Marchand & Bednarz, 1999, 2000 ; Radford, 2002 ; Schmidt & Bednarz, 1997) se sont intéressés aux caractéristiques des problèmes qui nécessitent une modélisation sous la forme d’une équation du premier degré à une inconnue.
Dans le domaine de la résolution proprement dite d’équations, Filloy et Rojano (1989, cités par Radford, 2002) font état des difficultés importantes éprouvées par les élèves lorsqu’il s’agit de résoudre des équations de la forme « ax + b = cx + d ». Le fait de devoir réaliser des opérations sur des nombres inconnus représente un obstacle important pour bon nombre d’élèves dans la mesure où aborder ce type d’équation dans une logique arithmétique s’avère souvent complexe. Dans cette optique, travailler sur des problèmes pouvant se modéliser sous cette forme serait dès lors intéressant pour amener les élèves à pleinement entrer dans le raisonnement algébrique.
D’autres chercheurs se sont intéressés aux caractéristiques des problèmes nécessitant une approche algébrique de résolution. Bednarz et Janvier (1993) ont ainsi défini deux structures de problèmes : dans les problèmes qu’elles qualifient de « connectés », des relations peuvent être établies entre des données connues, induisant un raisonnement de type arithmétique. À l’inverse, dans les problèmes qualifiés de « déconnectés », il n’est pas d’emblée possible d’établir de telles relations entre des données connues ; les démarches les plus efficaces pour résoudre ces problèmes seraient alors de nature algébrique.
Ce lien entre structure du problème et démarche de résolution privilégiée est toutefois remis en question par ces mêmes auteures dans leurs travaux plus récents. En effet, Bednarz et Janvier (2001) constatent que, dans un certain nombre de problèmes déconnectés, si certaines données sont inconnues, les relations qui unissent ces données sont en revanche connues, autorisant la mise en oeuvre de stratégies arithmétiques très efficaces qui ne s’appuient que sur ces relations connues. Kieran (2007) fait également état de recherches mettant en évidence des stratégies mixtes d’élèves débutant en algèbre qui consistent à modéliser le problème sous la forme d’une équation (témoignant d’une approche algébrique des problèmes puisque les éléments inconnus sont d’emblée pris en compte), puis à résoudre l’équation posée par une démarche arithmétique (à l’aide de stratégies d’essais-erreurs, notamment).
En définitive, Filloy, Rojano et Puig (2008) aboutissent au constat que l’analyse seule de l’énoncé ne permet pas de garantir l’efficacité exclusive de la démarche algébrique de résolution. Comme le montre l’extrait suivant, selon ces auteurs, pour identifier la nature de l’activité mathématique, il semble incontournable de mettre en relation la structure du problème avec la stratégie de résolution mise en place par la personne qui le résout.
Les chercheurs qui se sont intéressés à ces problèmes ont, au même moment, dû faire face à la difficulté de spécifier les différences entre les problèmes arithmétiques et algébriques. Cela les a amenés à des discussions sur la possibilité de réaliser une telle classification dichotomique, parce que les éléments qui composent le problème sont apparemment insuffisants pour le catégoriser. Il semble que ce soit la relation entre ces éléments et la stratégie de résolution mise en place par la personne qui résout le problème qui définisse la nature arithmétique ou algébrique de l’activité dans son ensemble
Filloy, Rojano, & Puig, 2008, p. 216, traduction libre
Les enjeux cognitifs de la mise en équation de problèmes arithmétiques
Plusieurs didacticiens ont étudié les démarches cognitives à mettre en oeuvre pour parvenir à modéliser un énoncé sous la forme d’une équation du premier degré à une inconnue (Bednarz & Janvier, 1993, 2001 ; Duval, 2002 ; Radford, 2002).
Radford (2002) met en évidence les particularités de la démarche algébrique consistant à passer d’un énoncé formulé en langage courant à son écriture symbolique sous la forme d’une équation. Cette démarche contraste de manière importante avec une analyse arithmétique du problème. Selon cet auteur, si l’écriture symbolique d’un énoncé sous forme d’équation raconte le problème tout autant que l’énoncé original, un travail cognitif important est à réaliser, et ce, pour deux raisons essentielles.
D’une part, entre l’énoncé original et son écriture symbolique à l’aide d’une équation, les personnages principaux changent : l’écriture symbolique met en avant certains aspects de l’histoire originale et en arrière-plan d’autres aspects. Ainsi, par exemple, pour formuler symboliquement l’expression « Kelly a 2 bonbons de plus que Manuel », une fois l’inconnue définie (le nombre de bonbons de Manuel, par exemple), il s’agit de s’intéresser non plus aux personnages (Kelly et Manuel) et à ce qu’ils possèdent chacun isolément, mais plutôt aux relations numériques qui les unissent (Kelly a 2 bonbons de plus que Manuel), pour en conclure que Kelly a en réalité x + 2 bonbons.
D’autre part, alors que l’histoire originale se déploie selon une lecture linéaire de gauche à droite (avec parfois des retours en arrière), l’écriture symbolique n’a pas de point d’entrée prédéfini.
Bref, entre les deux « histoires » (énoncé du problème et écriture symbolique), non seulement l’ordre du discours est différent, mais, en plus, ce discours porte sur d’autres aspects.
Duval (2002) précise les démarches nécessaires pour parvenir à passer d’un énoncé écrit en mots à sa modélisation sous la forme d’une équation. Selon lui, devant la mise en équation d’énoncés qu’il qualifie de non congruents (Duval, 1993, 2002) dans la mesure où il n’est pas possible de mettre directement en correspondance l’énoncé du problème et l’équation à écrire, les obstacles à surmonter sont de deux ordres :
la redésignation fonctionnelle d’objets, consistant à choisir une inconnue et à exprimer les objets évoqués dans l’énoncé en fonction de cette inconnue ;
l’explicitation d’une relation d’équivalence, qui amène à établir une équivalence entre des quantités connues et inconnues, exprimées sous la forme d’expressions algébriques.
Cet auteur souligne également que, lors de cette phase de conversion de l’énoncé sous la forme d’une équation, ce n’est pas le choix de l’inconnue (qui constitue l’une des étapes de la redésignation fonctionnelle) qui est le plus complexe à réaliser, mais plutôt l’explicitation de la relation d’équivalence.
Comparaison des apports des deux courants de recherche
Les travaux brièvement décrits ci-dessus amènent à s’interroger sur le pouvoir diagnostique du découpage de l’évaluation des compétences algébriques des élèves en trois phases, ainsi que sur la hiérarchie entre les phases de l’outil.
a) La question du pouvoir diagnostique des trois phases de l’outil
Une première comparaison des éléments présentés ci-dessus amène à pointer un premier problème concernant le choix même d’une tâche complexe. D’un côté, comme le préconisent Rey et ses collaborateurs (2006), il semble que ce n’est qu’au troisième degré que l’on peut réellement parler d’authentiques compétences, et que, devant ces tâches complexes, il est indispensable de laisser à l’élève le soin de choisir et d’organiser les procédures à utiliser pour proposer une réponse correcte à la tâche fournie. D’un autre côté, les recherches réalisées dans le domaine précis de la mise en équation de problèmes pointent le fait que la structure déconnectée du problème est une condition nécessaire, mais non suffisante pour garantir l’efficacité exclusive d’une démarche algébrique de résolution. Une mise en relation entre la nature du problème et la manière dont l’élève en réalise l’écriture symbolique est essentielle pour garantir la validité de contenu, qui est ici de résoudre un problème en mobilisant une équation du premier degré à une inconnue. Dès lors, est-il possible de trouver un énoncé de problème qui pourrait garantir que seule une procédure algébrique de résolution puisse être efficace ?
Une seconde comparaison des deux courants de recherche amène à s’interroger sur le pouvoir diagnostique des phases 2 et 3 de l’outil. Comment ces questions prennent-elles en compte les véritables enjeux cognitifs de la mise en équation d’un problème ? Parviennent-elles à diagnostiquer la manière dont les élèves réalisent le travail de redésignation fonctionnelledes objets décrits dans l’énoncé ? Permettent-elles de comprendre dans quelle mesure ils parviennent ou non à expliciter la relation d’équivalence ? Comment les élèves n’ayant pas mobilisé spontanément l’algèbre pour résoudre la tâche complexe parviennent-ils à mobiliser leurs acquis algébriques lorsqu’ils doivent plus explicitement les mobiliser dans le cadre de la réalisation de la tâche complexe décomposée (phase 2 de l’outil) ou dans le cadre d’exercices plus dépouillés (phase 3 de l’outil) ?
b) La question de la hiérarchie entre les trois phases de l’outil
Les recherches menées dans le domaine de l’évaluation des compétences mettent en évidence que les phases qui mesurent des procédures sont mieux réussies que les autres phases (Carette, 2007 ; Rey et al., 2006). Ce constat se confirme-t-il dans l’outil analysé ? Les élèves sont-ils plus performants lorsqu’il s’agit de résoudre la tâche complexe pouvant se modéliser à l’aide d’équations ou lorsqu’il s’agit de répondre à une série de questions plus ciblées directement sur la démarche algébrique, intégrées (phase 2) ou non (phase 3) dans un contexte particulier?
Méthodologie
Cet article se propose de mener une réflexion au départ d’un outil d’évaluation conçu par une des commissions d’outils mises en place par le ministère de l’Enseignement de la Fédération Wallonie-Bruxelles et disponible sur son site web officiel (www.enseignement.be) en guise d’exemple pouvant être utilisé par les enseignants dans leur classe pour évaluer les compétences de leurs élèves en algèbre selon un modèle en phases comme préconisé par Rey et ses collaborateurs (2006). Cet outil figure en annexe.
L’outil d’évaluation a été soumis en début d’année scolaire à 163 élèves de 3e année de l’enseignement secondaire (grade 9, élèves de 14-15 ans) issus de huit écoles situées en Fédération Wallonie-Bruxelles. Centré sur une facette de l’algèbre élémentaire, l’outil est décrit par ses concepteurs comme permettant d’évaluer les habiletés mathématiques suivantes : construction d’expressions littérales où les lettres ont le statut de variables ou d’inconnues, résolution d’équations du premier degré à une inconnue et calcul de valeurs numériques. Comme conseillé par les concepteurs, les élèves ont participé à une évaluation en deux phases distinctes : 20 minutes pour résoudre la tâche complexe (« le cadeau collectif ») et 50 minutes pour résoudre les phases 2 (tâche décomposée) et 3 (procédures) de l’outil.
Le choix de tester cet outil d’évaluation destiné aux élèves du premier degré de l’enseignement secondaire (grades 7-8) auprès d’élèves de 3e secondaire (grade 9) s’explique par le moment de passation (début d’année scolaire) et par la volonté de garantir que la mise en équation ait été vue préalablement dans toutes les classes. Un des attendus des outils d’évaluation de compétences est en effet de tester la capacité des élèves à mobiliser et à intégrer, devant des tâches complexes et inédites, des procédures apprises antérieurement.
Résultats
Les résultats sont structurés en deux parties. Dans la première partie, nous analysons les caractéristiques de l’outil en référence aux travaux de recherche présentés ci-dessus. Dans la seconde partie, nous analysons les résultats qui ressortent de la passation de l’outil selon un double point de vue : d’abord, une perspective centrée sur la difficulté des items et, ensuite, une approche centrée sur le profil des élèves en matière de réussite ou non dans les trois phases de l’évaluation. Dans les deux cas, les résultats sont interprétés en s’appuyant sur les démarches (arithmétiques ou algébriques) développées par les élèves devant les différentes tâches proposées.
Analyse du contenu de l’outil
En phase 1, la tâche complexe se présente sous la forme d’un bref énoncé.
Claude raconte à son copain :
« La semaine dernière, les élèves des classes de deuxième année ont décidé de se cotiser pour offrir un cadeau à Kevin, hospitalisé. Chacun a donné 0,50 €. Chargé de l’achat du cadeau, j’ai constaté qu’il manquait 15 €. J’ai réclamé 0,20 € supplémentaires par élève et j’ai alors eu 11 € de trop. »
Calcule le prix du cadeau. Écris les étapes de ton raisonnement et tous tes calculs.
Ce problème déconnecté particulier présente les caractéristiques mises en évidence par Bednarz et Janvier (2001) : si certaines données sont inconnues, les relations qui unissent ces données sont en revanche connues. Ce type de problème autorise alors deux types de démarches de résolution : la démarche algébrique attendue devant un problème déconnecté, mais aussi une démarche arithmétique très efficace qui ne s’appuie que sur ces relations connues.
En nous référant aux travaux de Duval (2002) et de Radford (2002), nous considérons que 5 étapes sont nécessaires pour résoudre le problème à l’aide de la démarche algébrique.
Identifier les quatre inconnues du problème : le prix du cadeau, le nombre d’élèves, la somme récoltée si chacun donne 0,50 € et la somme récoltée si chacun ajoute 0,20 € ;
-
Sélectionner une des inconnues (par exemple, le nombre d’élèves d’abord, soit n, puis le prix du cadeau, soit p) et exprimer les objets évoqués dans l’énoncé en fonction de l’inconnue choisie :
Si chaque élève donne 0,50 €, la somme récoltée s’élèvera à 0,50 • n ;
-
Si chaque élève ajoute 0,20 €, la somme récoltée s’élèvera à 0,70 • n ;
Le prix du cadeau surpasse de 15 € la somme récoltée si chaque élève donne 0,50 € (p = 0,50 • n + 15) et il vaut 11 € de moins que la somme récoltée si chaque élève ajoute 0,20 € (p = 0,70 • n - 11) ;
-
Expliciter la relation d’équivalence en s’appuyant sur le fait que le prix du cadeau (p) peut être exprimé de deux manières différentes :
p = 0,50 • n + 15
et
p = 0,70 • n - 11
⇔ 0,50 • n + 15= 0,70 • n - 11
-
Résoudre cette équation:
⇔ 0,50 • n + 15= 0,70 • n - 11
⇔ - 0,20 • n = - 26
⇔ n = 130
-
Interpréter la solution de l’équation : ce n’est pas le nombre d’élèves qu’il faut déterminer, mais le prix du cadeau :
⇔ p = 0,50 • 130 + 15 = 80.
Une démarche arithmétique s’appuyant sur les relations connues du problème peut également s’avérer tout à fait efficace : les 0,20 € versés en plus par chaque élève correspondent à une différence de 26 € (15 € + 11 €) sur le montant récolté. Grâce à cette information, on peut retrouver le nombre d’élèves (26 € : 0,20 € par élève = 130 élèves) et, de là, par une démarche analogue à celle présentée au point 5 ci-dessus, retrouver le prix du cadeau (0,50 • 130 + 15 = 80).
Les critères de correction de la tâche complexe tels qu’ils sont définis par les concepteurs de l’épreuve laissent une certaine autonomie à l’élève dans le choix de la démarche. Ainsi, l’élève aura réussi la tâche complexe s’il a trouvé le nombre d’élèves pour déterminer le prix du cadeau, s’il a tenu compte de tous les éléments de l’énoncé et s’il a établi des liens corrects entre ceux-ci. Par la suite, l’enseignant vérifiera si le calcul du prix du cadeau est correct et si la solution finale est présentée sous la forme d’une phrase.
Lors de la phase 2 de l’épreuve, l’énoncé de la tâche complexe est à nouveau soumis à l’élève, mais, cette fois, sous la forme d’une série de 7 étapes l’amenant à suivre pas à pas une démarche prédéfinie de résolution. À ce sujet, la marge de liberté laissée à l’élève quant au choix de la procédure de résolution est réduite puisque c’est la démarche algébrique qui a été privilégiée par les concepteurs, en lien avec les objectifs de l’outil qui portent explicitement sur ce domaine précis des mathématiques. D’emblée, le choix de l’inconnue est fourni à l’élève : « On appelle n le nombre d’élèves ». Les quatre premières étapes amènent à exprimer les objets évoqués dans l’énoncé en fonction de cette inconnue et à faire le lien avec le prix du cadeau. On accompagne ici l’élève dans la redésignation fonctionnelledes objets évoqués dans l’énoncé (Duval, 2002). La cinquième étape est centrée sur la mise en équation proprement dite (« Écris à présent une équation traduisant la situation ») et vise ainsi à cerner la capacité de l’élève à identifier la relation d’égalité. La sixième étape est consacrée à la résolution de l’équation produite (« Résous cette équation »), tandis que la dernière étape amène l’élève à calculer le prix du cadeau (« Calcule le prix du cadeau »).
La phase 3 de l’épreuve est composée d’une série de questions portant sur 1) la redésignation fonctionnelle des objets, l’explicitation de la relation d’équivalence et la résolution proprement dite d’un problème, 2) la résolution d’équations de difficultés variées, et 3) la vérification qu’un nombre est solution d’une équation.
En ce qui concerne les exercices portant sur la modélisation et sur la résolution de problèmes, la formulation des énoncés est telle qu’elle facilite souvent la phase de conversion de l’énoncé en équation (forte congruence, Duval, 1993). En accord avec le modèle de Rey et ses collaborateurs (2006), on est donc en effet plus proche d’une procédure à appliquer devant une tâche orientée (1er degré de compétences) que de la résolution d’une tâche élémentaire impliquant un « cadrage » et la mobilisation à bon escient d’une procédure (2e degré de compétences). Par contre, les questions posées dans cette phase 3 dépassent en complexité les procédures effectivement nécessaires pour résoudre la tâche complexe : par exemple, l’élève doit résoudre certaines équations impliquant des fractions, alors que ces dernières n’interviennent pas dans la tâche complexe. Cette caractéristique entre donc en contradiction avec les exigences posées par Rey et ses collaborateurs concernant la phase 3 de l’outil, à savoir qu’il convient d’évaluer les procédures exigées dans les phases 2 et 1, mais sous une forme décontextualisée.
Analyse des résultats à la suite de la passation de l’épreuve auprès de 163 élèves de 3e année du secondaire
Dans cette seconde partie, nous nous intéressons, d’une part, à la difficulté des items composant les différentes phases de l’outil et, d’autre part, à la façon dont les raisonnements écrits par les élèves « évoluent » tout au long des trois phases de l’outil. La comparaison de la difficulté des différents items relatifs à chacune des phases de l’outil permettra d’envisager la question de la hiérarchisation des phases. Une approche centrée sur les performances des élèves aux différentes phases de l’outil permettra quant à elle d’établir des profils d’élèves et de quantifier le nombre d’élèves appartenant à chacun d’entre eux.
L’analyse de la difficulté relative des items composant l’épreuve
Les tableaux 1 et 2 présentent les résultats obtenus à chaque phase de l’outil. Pour les phases 1 et 2, nous avons calculé la proportion d’élèves ayant réussi à trouver la solution du problème, tandis que, pour la phase 3, nous avons calculé le pourcentage moyen de réussite aux différentes tâches de la phase 3 ainsi que des indices de dispersion (écart-type, maximum et minimum).
Tableau 1
Résultats des phases 1 et 2 de l’outil
Tableau 2
Résultats de la phase 3 de l’outil
La hiérarchie entre les trois phases de l’outil, telle qu’attendue par le modèle de Rey et ses collaborateurs (2006), n’est dans ce cas pas respectée. En effet, si la phase 3 de l’outil est, en moyenne, mieux réussie que les deux autres phases, la décomposition en sous-problèmes (phase 2) est moins bien réussie que la tâche complexe (phase 1).
La possibilité d’obtenir une réponse correcte en appréhendant la question avec une approche arithmétique (c’est-à-dire ancrée dans le calcul sur des nombres connus) ou, au contraire, la nécessité de raisonner de manière algébrique (au départ de quantités inconnues) donne sens à la hiérarchie constatée. Alors que le raisonnement arithmétique est permis en phase 1, la phase 2 impose le recours à la modélisation sous la forme d’une équation. Même si, grâce à la décomposition, l’élève est guidé dans la mise en oeuvre d’une démarche algébrique en phase 2, celle-ci implique la mobilisation d’un domaine de connaissances qui est sans doute moins familier à certains élèves. Par ailleurs, pour les élèves qui ont résolu la tâche complexe par une démarche arithmétique en phase 1 (et ils sont 26 % dans ce cas, voir Tableau 3 ci-dessous), le changement de perspective imposé peut être relativement perturbant.
Tableau 3
Pourcentage d’élèves ayant mobilisé la démarche arithmétique ou algébrique lors de la phase 1
Au-delà de cette hiérarchie, il est aussi important de noter qu’une dispersion apparaît dans les résultats relatifs aux questions portant sur les procédures. Alors que certains élèves obtiennent un score moyen proche de 90 %, d’autres ne maîtrisent pas du tout les procédures, avec un score moyen de 15 %. Les items les plus complexes de l’outil concernent des procédures qui ne sont pas réellement nécessaires pour résoudre la tâche complexe (résolution d’équations fractionnaires et recherche de deux équations différentes qui permettent de modéliser un même problème). Il est par ailleurs intéressant de constater que certaines procédures algébriques figurent parmi les items les mieux réussis de l’outil : même les élèves les moins compétents ont à leur disposition un répertoire de procédures qu’ils devraient dès lors pouvoir mettre en oeuvre pour réaliser un traitement algébrique des situations. On peut penser qu’ils sous-exploitent néanmoins ce répertoire devant des problèmes, et ce, même s’ils sont guidés dans leur raisonnement (comme c’est le cas dans la phase 2 de l’outil).
L’approche centrée sur les performances des élèves aux différentes phases
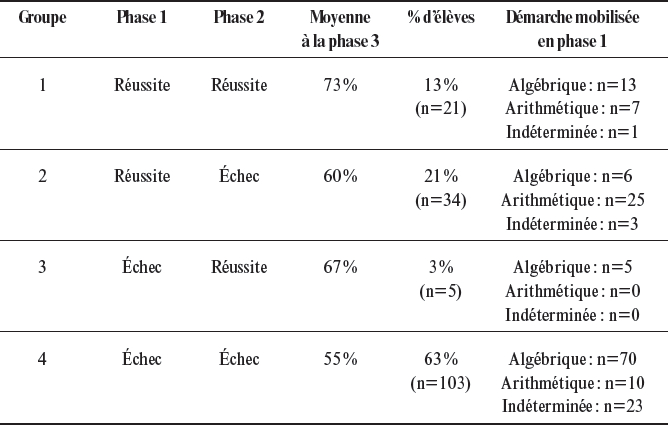
Une analyse centrée sur les performances des élèves aux différentes phases de l’outil permet d’éclairer les résultats sous un autre angle. Il est possible d’établir quatre profils distincts : les élèves qui ont réussi les deux premières phases de l’outil (groupe 1), les élèves qui ont réussi la première phase et échoué à la deuxième (groupe 2), ceux qui, à l’inverse, ont échoué à la première phase et ont réussi la deuxième (groupe 3), et enfin les élèves qui ont échoué aux deux phases (groupe 4). Cette analyse par profil d’élèves, dont les résultats sont présentés dans le tableau 4, comprend une analyse des démarches mobilisées dans la tâche complexe et le taux de réussite moyen de réussite à la phase 3 de l’outil.
Tableau 4
Résultats de l’analyse par profil d’élèves
Groupe 1
Le premier groupe se compose de 21 élèves. Il s’agit des élèves qui ont réussi les deux premières phases de l’outil. Ils obtiennent une moyenne de 73 % à la phase 3. Ce sont les plus compétents, tant en résolution de problèmes (phases 1 et 2) qu’en procédures (phase 3). Une analyse plus approfondie des démarches mobilisées par ces élèves pour résoudre la tâche complexe montre que seule une petite majorité d’entre eux (13 sur 21) a résolu le problème par l’algèbre.
Groupe 2
Le deuxième groupe, qui se compose de 34 élèves, se caractérise quant à lui par une réussite de la tâche complexe en phase 1, par un échec de la tâche décomposée en phase 2 et par une moyenne satisfaisante aux procédures (60 % en phase 3). Ce groupe, en rupture par rapport à la hiérarchie attendue entre les trois phases de l’outil, concerne un nombre considérable d’élèves (plus du cinquième des élèves testés est dans cette situation). On pourrait alors logiquement penser que ces élèves sont parvenus à résoudre la tâche complexe par une démarche arithmétique et qu’ils ne sont pas parvenus à entrer dans la démarche algébrique qui leur était imposée dans la phase 2 de l’outil. Cette hypothèse se vérifie dans 25 cas sur 34 ; les autres élèves ont développé soit une démarche algébrique (6 sur 34), soit une démarche qu’il était impossible de déterminer (3 sur 34). Les élèves de ce groupe ne parviennent pas à tirer profit de l’analyse algébrique de la situation proposée dans la phase 2 de l’outil, alors que les résultats obtenus à la phase 3 révèlent qu’ils disposent pourtant de compétences algébriques non négligeables (c’est-à-dire 60 % de réussite en moyenne pour la phase 3).
Groupe 3
Le groupe 3 est composé uniquement de 5 élèves. Ces élèves ont un bon répertoire de procédures (67 % de réussite en moyenne pour la phase 3) et parviennent à résoudre la tâche complexe lorsqu’ils sont guidés par des questions progressives. Dans tous les cas, ils ont tenté de mettre en place une démarche algébrique pour résoudre la tâche complexe en phase 1, celle-ci ayant été toutefois infructueuse. Il semble donc que seule cette faible minorité d’élèves (3 %) est réellement parvenue à tirer profit du guidage offert par la phase 2 de l’outil.
Groupe 4
Le groupe 4 rassemble à lui seul plus de la moitié des élèves (103 élèves). Ceux-ci ont une maîtrise satisfaisante des procédures algébriques (55 % de réussite à la phase 3 de l’outil), mais ne parviennent pas à résoudre la tâche complexe, qu’ils soient ou non accompagnés dans la démarche de résolution (phase 1 ou phase 2). Une analyse de leur démarche amène à constater que la plupart de ces élèves (70) ont tenté de résoudre la tâche complexe de manière algébrique, mais sans succès. En référence aux travaux de Duval (2002), nous pouvons penser que la phase 2 de l’outil ne les a pas aidés à réaliser les deux types d’opérations cognitives nécessaires pour parvenir à exprimer le problème sous la forme d’une équation (pour rappel, la redésignation fonctionnelledes objets et l’explicitation d’une relation d’équivalence). Une analyse de leurs productions confirme ce constat : bon nombre d’élèves n’identifient pas qu’il n’y a pas congruence entre l’énoncé en mots et sa désignation symbolique (par exemple, la proposition « il manque 15 € » est convertie par eux en l’expression symbolique « - 15 » dans l’équation « p = 0,50 • n - 15 »), ce qui les amène à une impasse.
Les moyennes des quatre groupes à la phase 3 de l’outil ont été comparées grâce à une analyse de la variance (ANOVA) [F(3;159)=9,965, p<0,001] et à un test post-hoc de Scheffé : il existe une différence statistiquement significative entre, d’une part, les moyennes des groupes 1 et 2 et, d’autre part, entre les moyennes des groupes 1 et 4.
Hormis le groupe 3, une proportion non négligeable d’élèves de chaque groupe a tenté de résoudre l’étape 1 en déployant une démarche arithmétique. On peut se demander si ces élèves tentent ainsi de contourner la difficulté que représente pour eux l’algèbre. Nous pouvons apporter un élément de réponse (voir Tableau 5) à cette question en analysant les moyennes obtenues à la phase 3 (procédures) de l’outil selon que les élèves ont réussi la tâche complexe par l’algèbre (groupe A), par l’arithmétique (groupe B) ou échoué à la tâche complexe (groupe C).
Tableau 5
Moyenne à la phase 3 de l’outil selon la manière dont les élèves ont appréhendé la tâche complexe
Si les élèves ayant réussi la tâche complexe de manière algébrique en phase 1 obtiennent, en phase 3, une moyenne supérieure à celle des élèves qui l’ont résolue de manière arithmétique, la moyenne de ces derniers est toutefois supérieure à ceux qui n’ont pas réussi à résoudre la tâche complexe. Ici encore, les moyennes des trois groupes à la phase 3 de l’outil ont été comparées grâce à une analyse de la variance [F(2;156)=12,356, p<0,001] et à un test post-hoc de Scheffé. Il existe une différence statistiquement significative entre les moyennes des groupes A et C, d’une part, et entre les moyennes des groupes B et C, d’autre part. Il semble donc que les élèves ayant réussi la tâche complexe par une démarche arithmétique ont un répertoire de procédures algébriques comparable à ceux qui ont résolu cette même tâche complexe par l’algèbre, mais qu’ils sous-investissent ce répertoire lorsqu’ils font face à un problème où la démarche de résolution ne leur est pas imposée et où l’utilisation d’une démarche arithmétique est possible.
Discussion
En s’appuyant sur divers constats de recherches menées dans le domaine de l’algèbre élémentaire (Bednarz & Janvier, 1993, 2001 ; Duval, 2002 ; Filloy, Rojano, & Puig, 2008 ; Kieran, 2007 ; Radford, 2002 ; Schmidt & Bednarz, 1997), la présente étude visait à éclairer le diagnostic qui peut ressortir d’un outil d’évaluation de compétences centré sur cette discipline. Analysés selon une double perspective, les résultats apportent des éléments empiriques aux deux problèmes définis, l’un s’intéressant à la hiérarchie des trois phases de l’outil et l’autre, à l’intérêt des deux dernières phases de l’outil pour éclairer le niveau de compétences des élèves et pour mieux cerner leurs lacunes.
La hiérarchie entre les trois phases, présumée par le modèle de Rey et ses collaborateurs (2006), n’est pas respectée pour cet outil. Si, de manière globale, la phase 3 de l’outil (centrée sur la maîtrise des procédures) est mieux réussie par les élèves que les deux autres phases, certains items évaluant des procédures apparaissent comme étant encore plus difficiles que la tâche complexe. Ce constat d’une dispersion des résultats de la phase 3 de l’outil se confirme également dans d’autres contextes (Marcoux, 2012 ; Dierendonck & Fagnant, 2014).
La tâche décomposée est moins bien réussie que la tâche complexe. Parmi les 66 % d’élèves qui échouent à la tâche complexe, seuls 3 % arrivent à tirer profit de la décomposition en sous-problèmes. Ces élèves avaient déjà tous mobilisé une ébauche de démarche algébrique pour tenter de résoudre la tâche complexe. À l’inverse, bon nombre d’élèves réussissent la tâche complexe en développant une démarche arithmétique de résolution. Ces élèves disposent pourtant d’un répertoire de procédures algébriques (comme en attestent leurs résultats en phase 3), qu’ils ont finalement sous-exploité devant la tâche complexe. Si cette sous-exploitation de leurs compétences algébriques ne leur a pas porté préjudice dans la résolution de la tâche complexe en phase 1, les constats sont tout à fait différents lorsqu’on essaie d’orienter leur démarche en phase 2. Ainsi, même guidés dans la démarche de résolution, ces élèves ne sont pas parvenus à entrer pleinement dans une résolution algébrique de la situation.
Ces résultats nous amènent à nous interroger sur l’intérêt de ce découpage en trois phases et sur l’opérationnalité même de la phase 2 (centrée sur une des manières seulement de résoudre la tâche complexe), dans ce contexte précis de mobilisation de l’outil « équation » pour résoudre un problème, et ce, pour diverses raisons.
Tout d’abord, la phase 1 de cet outil pose problème : comment dépasser ce paradoxe qui conduit à laisser une liberté aux élèves quant au choix de la méthode, tout en souhaitant tester leur capacité à résoudre un problème en mobilisant leurs acquis algébriques ? D’aucuns pensent qu’en choisissant bien les variables du problème, il est possible d’empêcher le développement de démarches arithmétiques efficaces. Cette idée n’est cependant pas pleinement partagée dans la littérature scientifique (Filloy, Rojano, & Puig, 2008 ; Marchand & Bednarz, 1999, 2000 ; Radford, 2002 ; Schmidt & Bednarz, 1997). De notre point de vue, une solution serait peut-être de considérer que l’expertise algébrique repose sur la capacité à utiliser, dans des situations appropriées, tantôt les acquis liés à la connaissance du numérique, tantôt les acquis purement algébriques. Dans ce cas, l’analyse de la démarche mise en oeuvre par l’élève non pas face à une seule tâche complexe, mais à plusieurs pourrait permettre d’affiner le diagnostic et d’éviter que la véritable compétence de l’élève ne soit jugée qu’à travers la capacité à résoudre un seul problème particulier.
La phase 2 de l’outil pose également problème : elle a pour objectif d’amener l’élève à entrer pas à pas dans une réflexion algébrique du problème, c’est-à-dire à mettre en avant-plan certains aspects de l’énoncé et à les relier entre eux pour élaborer l’équation. L’analyse qualitative de cette phase 2 amène à constater que, si quatre questions sont centrées sur la redésignation fonctionnelledes objets évoqués dans l’énoncé, l’explicitation de la relation d’équivalence est peu étayée puisque seule la phrase « Écris à présent une équation traduisant la situation » les guide dans cette démarche. Pourtant, Duval (2002) mentionne le fait que l’explicitation de la relation d’équivalence s’avère être une démarche plus complexe à mettre en oeuvre que celle relative à la redésignation fonctionnelle des objets. Par ailleurs, les résultats obtenus par les élèves testés à cette phase 2 de l’outil pointent le faible pouvoir diagnostique de cette phase : seuls 3 % des élèves semblent réellement tirer profit de l’étayage proposé dans cette phase 2 de l’outil.
En ce qui concerne la phase 3, si on peut comprendre la volonté des concepteurs d’élaborer un diagnostic plus approfondi de la maîtrise des techniques algébriques impliquées dans la résolution d’un problème par mise en équation, cette phase se détourne à nouveau de l’objectif initial tel qu’il a été défini par Rey et ses collaborateurs (2006), qui était de mesurer la maîtrise des procédures nécessaires à la réalisation de la tâche. La nature même des équations soumises aux élèves dépasse en complexité les techniques algébriques nécessaires pour résoudre l’équation à produire dans la réalisation de la tâche complexe : le diagnostic posé grâce à la passation de la phase 3 de l’outil manque donc également de validité si on le considère dans le cadre du modèle théorique dont l’outil s’inspire.
Dans cet article, nous avons voulu montrer l’intérêt de combiner un apport des recherches menées dans le domaine de l’algèbre élémentaire pour éclairer le diagnostic que nous pouvions tirer d’un outil conçu dans une perspective plus générale d’évaluation des compétences. Les résultats obtenus montrent la difficulté de l’identification des ressources nécessaires pour résoudre une tâche complexe. Il s’agit là d’une question fondamentale dans l’élaboration de tâches valides : des essais préliminaires de l’outil, accompagnés d’une analyse systématique des stratégies (correctes mais aussi erronées) mises en oeuvre par les élèves, semblent primordiaux à l’élaboration de telles épreuves.
Notre réflexion présente un certain nombre de limites. Ainsi, un seul outil est passé au crible : il serait sans aucun doute nécessaire de réaliser une telle analyse au départ d’autres outils également centrés sur les compétences algébriques des élèves. Par ailleurs, afin de nous assurer que les élèves ont bénéficié d’un enseignement des compétences au coeur de l’outil, nous avons soumis l’épreuve à des élèves de début de 3e secondaire (grade 9), et non de 2e année (grade 8) comme préconisé par les concepteurs de l’outil. On peut imaginer que les élèves de 3e année, qui ne viennent pas d’aborder cette matière en classe, recourent à des stratégies plus variées, ce qui pourrait encore amplifier le phénomène de décalage entre les démarches utilisées dans la phase 1 de l’outil et dans les deux autres phases.
Au vu des résultats et des développements théoriques récents, il apparaît que l’identification des ressources nécessaires pour résoudre une tâche complexe s’avère extrêmement difficile à réaliser dans le contexte des premiers apprentissages algébriques (voir le débat sur le lien entre structure connectée ou déconnectée des problèmes et nature de l’activité mathématique). Or, il s’agit d’une question fondamentale dans l’élaboration d’un diagnostic valide. Ce point d’entrée a été largement développé dans le cadre d’une réflexion plus large sur l’élaboration d’un diagnostic réalisé selon une analyse globale multidimensionnelle des connaissances et des activités des élèves en algèbre (Grugeon et al., 2012). Ces auteures plaident pour une « articulation entre travail microscopique et travail macroscopique […] en vue de fiabiliser l’interprétation de l’activité algébrique des élèves » (Grugeon et al., 2012, p. 19). Il s’agit ainsi de combiner des approches quantitatives avec des approches qualitatives en vue de mieux interpréter les caractéristiques des raisonnements algébriques produits par les élèves. Les constats réalisés dans notre étude plaident également pour la nécessité d’analyser selon différents points de vue les résultats des élèves lors de la passation des outils mis à la disposition des enseignants.
D’autres compléments pourraient aussi être apportés par les recherches qui se sont intéressées spécifiquement à la résolution de problèmes mathématiques.
Sur le plan de l’apprentissage, les recherches notamment menées par Julo (2002) montrent l’intérêt d’une analyse conjointe du fonctionnement cognitif des élèves, d’une part, et des caractéristiques du problème à résoudre, d’autre part. Pour lui, tout l’enjeu est d’élaborer des aides permettant aux élèves de garder la main sur l’invention de la démarche de résolution : les amener à progresser dans leur représentation du problème, au cours même de la démarche de résolution, semble plus porteur que de leur expliquer a posteriori comment ils auraient dû s’y prendre. Les recherches portant sur la construction de représentations en résolution de problèmes et sur la façon dont l’enseignant peut travailler avec les élèves pour les aider à ce niveau sont nombreuses, tant sur le plan des perspectives influencées par la psychologie cognitive (voir notamment Julo, 2002 ; Thevenot, Barouillet, & Fayol, 2010) que d’une perspective socioculturelle (voir notamment Van Dijk, Van Oers, & Terwel, 2003 ; voir aussi Fagnant & Vlassis, 2013). La prise en compte de ces travaux pourrait non seulement éclairer les résultats de recherches relatifs à la mesure des compétences des élèves devant les tâches complexes, mais aussi apporter des éléments pour réfléchir à différents types d’aide à fournir aux élèves « perdus » devant la tâche complexe, sans pour autant les guider pas à pas dans une démarche correcte de résolution. Dans cette perspective, il serait intéressant d’approfondir la possibilité de fournir des « indices » aux élèves, comme c’est le cas dans l’optique qui a été prise pour les outils d’évaluation destinés aux élèves à la fin de l’enseignement secondaire en Fédération Wallonie-Bruxelles (Carette & Dupriez, 2009).
Appendices
Annexe
Outil d’évaluation analysé – Le cadeau collectif[*]
Phase 1
Contexte
Claude raconte à son copain :
« La semaine dernière, les élèves des classes de deuxième année ont décidé de se cotiser pour offrir un cadeau à Kevin, hospitalisé. Chacun a donné 0,50 €. Chargé de l’achat du cadeau, j’ai constaté qu’il manquait 15 €. J’ai réclamé 0,20 € supplémentaires par élève et j’ai alors eu 11 € en trop. »
Tâche
Calcule le prix du cadeau. Écris les étapes de ton raisonnement et tous tes calculs.
Phase 2
1. Claude raconte à son copain :
« La semaine dernière, les élèves des classes de deuxième année ont décidé de se cotiser pour offrir un cadeau à Kevin, hospitalisé. Chacun a donné 0,50 €. Chargé de l’achat du cadeau, j’ai constaté qu’il manquait 15 €. J’ai réclamé 0,20 € supplémentaires par élève et j’ai alors eu 11 € en trop. »
On appelle n le nombre d’élèves.
Écris, en fonction de n, le montant récolté en demandant 0,50 € à chaque élève.
-
Comment pourrait-on calculer le prix du cadeau si on connaissait ce montant ?
Écris une expression littérale qui traduit ce calcul.
-
Claude réclame 0,20 € de plus. Écris le nouveau montant demandé à chaque élève.
Écris, en fonction de n, le montant récolté en demandant ce nouveau montant à chaque élève.
-
Comment pourrait-on calculer le prix du cadeau si on connaissait ce montant ?
Écris une expression littérale qui traduit ce calcul.
Écris à présent une équation traduisant la situation.
Résous cette équation.
Calcule le prix du cadeau.
Phase 3
2. Entoure la (ou les) équation(s) permettant de résoudre chacun des problèmes suivants.
Précise, à chaque fois, ce que représente l’inconnue.
-
Martine a deux fois plus d’argent que son frère Didier.
À eux deux, ils possèdent 210 €. Combien Didier possède-t-il ?
s + s/2 = 210
2s + s = 210
2s + 210 = s
2 (s + s) = 210
inconnue :
-
Quel nombre est égal à son opposé augmenté de 16 ?
x = - (x + 16)
x = x – 16
- x = x + 16
x = - x + 16
inconnue:
-
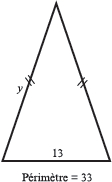
Que mesurent les côtés d’un triangle isocèle dont le périmètre mesure 34 cm si la base mesure 2 cm de moins que les autres côtés ?
x . (x - 2) = 34
3x - 2 = 34
2x - 2 = 34
3x + 2 = 34
inconnue :
3. Résous les équations suivantes :
13 (x - 3) = 52
2x + 13 = 4x - 7


4.
-
Jean propose 5 comme solution de l’équation 2 (5x – 1) = 3 (4x – 8).
Marie prétend qu’il se trompe. Pourtant, elle n’a pas résolu l’équation.
Explique comment elle a procédé.
-
Pour chaque ligne du tableau, entoure la (ou les) affirmation(s) juste(s).
1°
L’égalité 3x = 3 est vérifiée par
x = 0
x = -1
x = 1
2°
-3 est la solution de l’équation
3x - 1 = -10
2x + 3 = -3
4x + 9 = 4
5.
6. la balance est en équilibre. calcule la masse de chaque bidon. Explique.

7. complète chaque calcul.
Références
- Beckers, J. (2012). Introduction et mise en perspective théorique. Dans J. Beckers, J. Crinon & G. Simons (dir.), Approche par compétences et réduction des inégalités d’apprentissage entre élèves : de l’analyse des situations scolaires à la formation des enseignants (pp. 7-16). Bruxelles : De Boeck.
- Bednarz, N., & Janvier, B. (1993). The arithmetic-algebra transition in problem solving : Continuities and discontinuities. In J. R. Becker & B. J. Pence (Eds.), Proceedings of the 15th annual meeting of the International Group for the Psychology of Mathematics Education North American Chapter (Vol. II, pp. 19-25). Asilomar (CA).
- Bednarz, N., & Janvier, B. (2001). Emergence and development of algebra as a problem-solving tool: Continuities and discontinuities with arithmetic. In N. Bednarz, C. Kieran & L. Lee (Eds.), Approaches to algebra: Perspectives for research and teaching (pp. 115-136). Dordrecht : Kluwer Academic Publisher.
- Carette, V. (2007). L’évaluation au service de la gestion des paradoxes liés à la notion de compétence. Mesure et évaluation en éducation, 30(2), 49-71.
- Carette, V., & Dupriez, V. (2009). La lente émergence d’une politique scolaire en matière d’évaluation des élèves : quinze ans de transformations en Belgique francophone. Mesure et évaluation en éducation, 32(3), 23-46.
- Communauté française de Belgique (1997). Décret définissant les missions prioritaires de l’enseignement fondamental et de l’enseignement secondaire et organisant les structures propres à les atteindre. Bruxelles : Moniteur belge.
- Crahay, M., & Detheux, M. (2005). L’évaluation des compétences, une entreprise impossible ? Résolution de problèmes complexes et maîtrise de procédures mathématiques. Mesure et évaluation en éducation, 28(1), 57-78.
- De Ketele, J.-M., & Gérard, F.-M. (2005). La validation des épreuves d’évaluation selon l’approche par les compétences, Mesure et évaluation en éducation, 28(3), 1-26.
- Dierendonck, C., & Fagnant, A. (2014). Approche par compétences et évaluation à large échelle : deux logiques incompatibles ? Mesure et évaluation en éducation, 37(1), 43-82.
- Duval, R. (1993). Registres de représentation sémiotique et fonctionnement cognitif de la pensée. Annales de didactique et de sciences cognitives, 5, 37-65.
- Duval, R. (2002, décembre). L’apprentissage de l’algèbre et le problème cognitif de la désignation des objets. Actes du Séminaire franco-italien sur l’enseignement de l’algèbre. IREM, Nice, France.
- Eurydice (2012). Developing key competences at school in Europe: Challenges and opportunities for policy. Eurydice Report. Luxembourg: Publications Office of the European Union.
- Fagnant, A., & Vlassis, J. (2013). Schematic representations in arithmetical problem solving: Analysis of their impact on grade 4 students. Educational Studies in Mathematics, 84, 149-168. doi: 10.1007/s10649-013-9476-4
- Filloy, E., Rojano, T., & Puig, L. (2008). Educational algebra: A theoretical and empirical approach. New York: Springer.
- Grugeon, B., Pilet, J., Chenevotot, F., & Delozanne, E. (2012). Diagnostic et parcours différenciés d’enseignement en algèbre élémentaire. Recherches en didactique de mathématiques, « Enseignement de l’algèbre : bilan et perspectives, hors série », 137-162.
- Julo, J. (2002). Des apprentissages spécifiques pour la résolution de problèmes ? Grand N, 69, 31-52.
- Kieran, C. (2007). Learning and teaching algebra at the middle school through college levels: Building meaning for symbols and their manipulation. In F. K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 707-762). Greenwich (CT): Information Age Publishing.
- Lafontaine, D. (2012, janvier). Des politiques aux pratiques d’évaluation en Belgique francophone: la cohérence en questions. Actes du 24e Colloque international de l’ADMEE-Europe, Luxembourg (Luxembourg). Récupéré de http://admee2012.uni.lu/pdf2012/S8_B.pdf
- Marchand, P., & Bednarz, N. (1999). L’enseignement de l’algèbre au secondaire : une analyse des problèmes présentés aux élèves. Bulletin AMQ, 39(4), 30-42.
- Marchand, P., & Bednarz, N. (2000). Développement de l’algèbre dans un contexte de résolution de problèmes. Bulletin AMQ, 40(4), 15-25.
- Marcoux, G. (2012). Différences entre élèves dans trois types de tâches en mathématiques : quelques variables à prendre en compte pour éviter d’engendrer des inégalités. Dans J. Beckers, J. Crinon & G. Simons (dir.). Approche par compétences et réduction des inégalités d’apprentissage entre élèves (pp. 33-56). Bruxelles : De Boek.
- Radford, L. (2002). On heroes and the collapse of narratives: A contribution to the study of symbolic thinking. In A. D. Cockburn & E. Nardi (Eds.) Proceedings of the 26th annual meeting of the International Group for the Psychology of Mathematics Education (Vol. 4, pp. 81-88). Norwich, England.
- Rey, B., Carette, V., Defrance, A., & Kahn, S. (2006). Les compétences à l’école : apprentissages et évaluation (2e éd.). Bruxelles : De Boeck.
- Scallon, G. (2007). L’évaluation des apprentissages dans une approche par les compétences (2e éd.). Bruxelles : De Boeck Université.
- Schmidt, S., & Bednarz, N. (1997). Raisonnements arithmétiques et algébriques dans un contexte de résolution de problèmes : difficultés rencontrées par les futurs enseignants. Educational Studies in Mathematics, 32(2), 127-155.
- Thevenot, C., Barrouillet, P., & Fayol, M. (2010). De l’émergence du savoir calculer à la résolution des problèmes arithmétiques verbaux. Dans M. Crahay & M. Dutrevis (dir.), Psychologie des apprentissages scolaires (pp. 137-166). Bruxelles : De Boeck.
- Van Dijk, I., Van Oers, B., & Terwel, J. (2003). Providing or designing? Constructing models in primary maths education. Learning and Instruction, 13, 53-72.
Appendices
Note
-
[*]
Cet outil a été élaboré par la Commission des outils d’évaluation pour l’enseignement secondaire en mathématiques, mise en place par le ministère de l’Éducation de la Fédération Wallonie-Bruxelles.
List of tables
Tableau 1
Résultats des phases 1 et 2 de l’outil
Tableau 2
Résultats de la phase 3 de l’outil
Tableau 3
Pourcentage d’élèves ayant mobilisé la démarche arithmétique ou algébrique lors de la phase 1
Tableau 4
Résultats de l’analyse par profil d’élèves
Tableau 5
Moyenne à la phase 3 de l’outil selon la manière dont les élèves ont appréhendé la tâche complexe







 10.7202/1024930ar
10.7202/1024930ar