Enseigner la résolution de problèmes écrits de mathématiques au primaire : pratiques déclarées des enseignants des deuxième et troisième cycles Teaching Mathematical Word Problem Solving in Primary School: Reported Practices of Teachers in the Second and Third Cycles

Résumé

La nature des pratiques enseignantes au regard des méthodes de résolution de problèmes écrits de mathématiques, notamment le quoi (quelle méthode, ses avantages et ses inconvénients), le comment (les exigences d’utilisation envers les élèves) et le pourquoi (les raisons de l’utilisation), représente un sujet très peu documenté dans la littérature scientifique. Le présent article vise à exposer les principaux résultats de la première phase d’une programmation de recherche plus large dont l’objectif était de décrire les pratiques relatives aux méthodes de résolution de problèmes écrits de mathématiques présentées par les enseignants des deuxième et troisième cycles du primaire.

Mots-clés :

• Résolution de problèmes écrits de mathématiques,
• méthodes de résolution de problèmes,
• pratiques déclarées des enseignants,
• enseignement primaire

Abstract

The nature of teaching practices regarding word problem solving methods, including the what (which method, its advantages and disadvantages), the how (the teachers’ requirements towards the students use of the method), and the why (the reasons for using it) represents a very little documented subject in scientific literature. This paper will present the main results of the first phase of a larger research program, which its primary objective was to describe the elementary school teachers’ practices relating to mathematical word problem solving methods.

Keywords:

• Mathematical word problems,
• problem solving methods,
• teachers’ practices,
• elementary education

Mise en contexte

Le projet dont il est question dans cet article renvoie à la première phase d’un projet doctoral s’inscrivant dans le domaine de la recherche en résolution de problèmes écrits de mathématiques. Il tire son origine de l’hypothèse générale selon laquelle il semble y avoir un écart important entre les modèles de résolution de problèmes proposés par la recherche et la façon dont ces modèles ont été récupérés en méthodes pouvant être présentées aux élèves du primaire. Les chercheurs ayant travaillé à modéliser le processus de résolution de problèmes insistent sur l’importance de s’engager dans une démarche cyclique et itérative (Fagnant et al., 2003 ; Greer, 1997 ; Hanin et Van Nieuwenhoven, 2018 ; Pólya, 1945 ; Verschaffel et al., 2000) en se créant une représentation mentale du problème allant au-delà des informations présentées explicitement, c’est-à-dire en dégageant des informations implicites (Kintsch, 1998 ; Österholm, 2006 ; Reusser, 2000 ; Van Dijk et Kintsch, 1983). Selon le ministère de l’Éducation de l’Ontario (2006), les modèles de résolution de problèmes pour l’enseignement des mathématiques devraient être introduits dans les classes avec souplesse :

L’enseignant ou l’enseignante devrait modeler diverses façons d’utiliser les étapes du modèle […]. Les élèves comprendront alors qu’il est possible, par exemple, d’élaborer un plan pour résoudre un problème et de s’apercevoir, en exécutant le plan ou à la fin du processus, qu’il faut recommencer et essayer autre chose. Il est très important de se rappeler que le but premier de la résolution de problèmes est davantage de donner un sens aux mathématiques que de maîtriser les étapes d’un processus ou un ensemble de stratégies

p. 44

Dans le même ordre d’idées, Wilson et ses collègues (1993) soulignent qu’une utilisation séquentielle d’un modèle de résolution de problèmes peut avoir plusieurs effets négatifs, dont conduire les élèves à se concentrer principalement sur l’atteinte de la solution, faisant référence à la résolution proprement dite. C’est ce que De Corte (2012) appelle la « mise entre parenthèse du sens » (« suspension of sense-making »), c’est-à-dire cette tendance qu’ont les élèves à omettre certaines étapes du processus de résolution de problème, principalement celle de la compréhension du problème. Or, la résolution (réussie) du problème doit nécessairement s’appuyer sur une bonne compréhension, qui se traduit par une représentation adéquate de la situation dans laquelle s’inscrit le problème (De Corte, 2012 ; Fagnant et Demonty, 2004). « La construction d’une représentation du problème et donc, la prise en compte du contexte de ce dernier, conditionne la réussite des phases de résolution ultérieures et donc la réussite du problème » (Hanin et Van Nieuwenhoven, 2016, p.57). De plus, sachant que les tentatives faites par le solutionneur pour trouver la solution l’amènent à changer son point de vue, sa façon de voir le problème, et ce, à plusieurs reprises, plusieurs auteurs insistent sur le caractère cyclique et itératif des différentes étapes d’un processus de résolution de problèmes (Fagnant et al., 2003 ; Greer, 1997 ; Pólya, 1973 ; Verschaffel et al., 2000). Nous retenons de ces propos deux éléments en particulier. Premièrement, le processus de résolution de problèmes ne devrait pas se traduire par une utilisation systématique d’étapes à suivre de façon systématique et séquentielle, et deuxièmement, un processus authentique de résolution de problèmes implique différents allers-retours entre les différentes phases (non linéaires) de la démarche de résolution, y compris la représentation du problème qui est déterminante, « car elle conditionne la réussite des étapes ultérieures » (Fagnant et Demonty, 2004, p.15).

À l’opposé de ces recommandations issues de la recherche, les données issues d’une phase préliminaire durant laquelle 10 entrevues ont été réalisées auprès d’enseignants du primaire suggèrent que la pratique semble davantage orientée vers l’application de méthodes séquentielles. Autrement dit, pour résoudre les problèmes qui leur sont proposés, les élèves semblent devoir appliquer une série d’étapes dans un ordre précis.

L’utilisation d’une méthode en particulier, soit la méthode de type « ce que je sais, ce que je cherche », parfois appelée la démarche en croix, semble être un bon exemple témoignant de l’écart entre la recherche et la pratique. Afin de vérifier l’existence de cet écart, mais aussi dans le but d’étudier les conséquences possibles (de l’hypothèse) d’un écart, notre projet de recherche a été mené selon trois phases subséquentes. La première phase de l’étude, dont il est question dans cet article, a permis de recueillir des données quantitatives et qualitatives concernant les pratiques relatives à l’enseignement de la résolution de problèmes écrits de mathématiques de 143 enseignants des deuxième et troisième cycles du primaire (8 à 12 ans) ayant rempli un questionnaire en ligne.

Situation problématique et cadre théorique

À la suite de la parution d’un nouveau programme au primaire en 1980 (MEQ), un document pédagogique connu sous le nom du Fascicule K (1988) a été produit quelques années plus tard en tant que guide pédagogique traitant spécifiquement de la résolution de problèmes en mathématiques. La portée de ce document était de clarifier la façon d’aborder la résolution de problèmes mathématiques au primaire en proposant des recommandations et en insistant sur « le développement d’une habileté générale à résoudre des problèmes » (Fascicule K, 1988, p.9). Depuis la publication du Fascicule K, la résolution de problèmes écrits de mathématiques est décrite non seulement comme un objet d’apprentissage en soi, mais aussi comme une façon de construire de nouvelles connaissances mathématiques. En ce sens, Bednarz et Lajoie (2018) expliquent que les enseignants des années 1980-1990 sont désormais encouragés à travailler la résolution de problèmes en tant « qu’habileté de base à développer et comme moyen à privilégier dans l’enseignement pour développer des connaissances, des habiletés, des attitudes et des stratégies de résolution de problèmes » (p.430). Dionne et Voyer (2009) parlent pour leur part d’une double finalité : la résolution de problèmes comme objet d’étude et comme approche pédagogique.

Ces deux finalités associées à l’activité de résolution de problèmes en mathématiques ne se retrouvent pas uniquement dans les curriculums québécois. Une analyse des documents officiels de pays et régions francophones (Québec, France, Suisse romande et Communauté française de Belgique) effectuée par Fagnant et Vlassis (2010) a amené les auteurs à conclure que les programmes reconnaissent l’importance des processus de résolution de problèmes à développer, tout en considérant la résolution de problèmes comme une modalité pédagogique.

Des liens très étroits peuvent être établis entre ces deux finalités décrites par Fagnant et Vlassis (2010) et celles décrites par Dionne et Voyer (2009). La finalité « modalité pédagogique » renvoie à la finalité « approche pédagogique », qui fait référence à un outil de développement de connaissances, tandis que la finalité « processus même de résolution de problèmes » correspond à la finalité « objet d’étude », qui renvoie au développement de stratégies et d’habiletés propres à l’activité de résolution de problèmes.

Plus récemment, le ministère de l’Éducation et de l’Enseignement supérieur (2019) a souligné qu’au cours des quarante dernières années, les recherches réalisées en didactique des mathématiques ont permis de mettre en évidence qu’un des fondements de l’activité mathématique consiste en fait à recourir à la résolution de problèmes selon différentes intentions, dont « apprendre les concepts et les processus mathématiques » et « développer des stratégies cognitives et métacognitives au service de la résolution de problèmes » (p.10).

Bien que la résolution de problèmes soit considérée comme faisant partie intégrante de l’activité mathématique et que différentes finalités (ou intentions) y soient associées, la façon dont cette activité est travaillée auprès des élèves ne semble pas être orientée vers la poursuite des différentes finalités décrites par la littérature et les différents programmes de formation. À ce sujet, Savard et Polotskaia (2014) ont interrogé 12 enseignants québécois du primaire concernant les motifs guidant leurs choix de problèmes et leurs interventions durant l’activité de résolution de problèmes écrits à structures additives. Les auteures ont ensuite analysé les réponses des enseignants de façon à définir les rôles attribués (et les contextes suggérés) à la résolution de problèmes. Elles notent que les enseignants interrogés semblent valoriser le rôle « favoriser la mobilisation de concepts mathématiques déjà appris » (p. 145). À ce propos, Savard et Polotskaia (2014) soutiennent que :

Le rôle consistant à mobiliser des concepts mathématiques dans la résolution de problèmes est lié à une réutilisation des concepts. Dès lors, la tâche a été perçue principalement comme une occasion d’utiliser des connaissances déjà acquises et non pas comme une occasion d’acquérir de nouvelles connaissances

p. 145

Les résultats de ces auteures permettent de comprendre que l’utilisation des problèmes dits d’application ou routiniers, utilisés dans le but de réutiliser des concepts enseignés préalablement, ne semble pas permettre l’atteinte de la finalité « approche pédagogique ». L’utilisation de ce type de problème permet-elle alors l’atteinte de l’autre finalité (objet d’étude) ? Pas nécessairement. Pour répondre à cette question, il faudrait plutôt se poser la question suivante : comment la finalité « objet d’étude » est-elle abordée dans les classes du primaire ? Autrement dit, comment les élèves sont-ils formés à devenir de bons solutionneurs, qui renvoie à l’objectif ultime de cette finalité ? Une avenue pouvant être envisagée pour répondre à cette question est celle des stratégies et des modèles de résolution de problèmes utilisés dans les classes : « Quelles sont les stratégies de résolution de problèmes enseignées aux élèves du primaire ? Quels sont les modèles de résolution de problèmes présentés aux élèves ? » Ces questions sont importantes puisque toute stratégie ou tout modèle de résolution de problèmes ne conduit pas nécessairement à former les élèves à devenir de bons solutionneurs, capables « d’analyser une situation, de prendre les bonnes décisions, mais aussi de réfléchir aux relations sous-jacentes et de les rapporter aux solutions » (Organisation de coopération et de développement économique (OCDE), 2004, p. 30). À titre d’exemple, plusieurs études rapportent que des stratégies telles que « Repérer les mots-clés qui indiquent l’opération à effectuer », « Identifier les informations importantes » ou « Repérer des indices » figurent parmi les stratégies de résolution de problèmes les plus enseignées par les enseignants du primaire (Bruun, 2013 ; Fagnant et Burton, 2009 ; Seifi et al., 2012), et ce, même si certaines d’entre elles sont reconnues comme étant des stratégies superficielles. À ce sujet, Hanin et Van Nieuwenhoven (2018) expliquent que le terme superficiel renvoie à cette idée d’analyse linéaire, parfois même uniquement numérique, qui veut qu’un problème puisse être résolu directement par l’application d’une opération arithmétique connue de l’enfant en utilisant les nombres repérés dans l’énoncé. Ces auteures ajoutent que le problème est alors analysé par l’élève non pas en matière de structure mathématique, mais selon des traits superficiels. C’est le cas de la stratégie « repérer des mots-clés qui indiquent l’opération à effectuer » qui ne semble pas être un choix pédagogique favorisant l’atteinte de la finalité « objet d’étude » puisqu’elle amène simplement les élèves à repérer des mots-clés, sans comprendre la relation existante entre ces mots-clés et le contexte dans lequel ils s’inscrivent (Rosales et al., 2012 ; Van de Walle, 2010 ; Verschaffel et al., 2000). Autrement dit, cette stratégie peut être considérée comme étant superficielle lorsque le choix d’une opération mathématique est basé sur la sélection d’un mot isolé plutôt que sur une analyse en profondeur de la situation dans laquelle s’inscrit le problème (Verschaffel et De Corte, 1997). La question des stratégies enseignées aux élèves ayant été grandement documentée (Bruun, 2013 ; De Corte et Verschaffel, 1987 ; Fagnant et Burton, 2009 ; Muir et al., 2008 ; Seifi et al., 2012 ; Torbeyns et al., 2005), nous avons plutôt choisi d’étudier la question des modèles de résolution de problèmes mathématiques présentés dans les classes du primaire, à propos de laquelle les connaissances sont plus limitées.

En effet, au cours des dernières années, certaines études ont cherché à évaluer l’effet de programmes d’intervention (aussi appelés dispositifs d’enseignement-apprentissage) élaborés dans le but d’aider les élèves à développer, entre autres, leurs compétences en résolution de problèmes mathématiques (De Corte et al., 2004 ; Hanin et Van Nieuwenhoven, 2016 ; Perels et al., 2005 ; Verschaffel et al., 1999). C’est le cas de l’étude de Verschaffel et son équipe (1999) qui ont utilisé un devis quasi expérimental de type prétest/posttest/test de rétention avec groupe témoin afin de vérifier l’effet de leur programme d’enseignement sur l’acquisition d’un modèle compétent de résolution de problèmes mathématiques. Le modèle développé par Verschaffel et ses collègues (1999) comporte cinq niveaux, auxquels sont associées huit stratégies spécifiques (appelées heuristiques). Le modèle sert en fait de stratégie générale de résolution de problèmes pouvant être travaillée auprès des élèves et vise notamment à amener les élèves à prendre conscience des différentes phases intervenant dans un véritable processus de résolution de problème (dit compétent ou authentique). L’expérimentation a été menée auprès de quatre classes de cinquième année du primaire à Louvain, en Belgique. L’équipe de recherche a élaboré un total de 20 séances d’enseignement s’échelonnant sur une période de quatre mois, dont l’animation a été prise en charge par les enseignants des classes expérimentales, à la suite d’une formation et d’un accompagnement étroit offerts par l’équipe de recherche. Les résultats soutiennent qu’il est possible d’amener les élèves à développer leurs compétences en résolution de problèmes par l’enseignement de stratégies métacognitives et d’heuristiques spécifiques, dispensé dans un environnement éducatif qui propose des problèmes variés, riches et authentiques. Une telle conclusion s’avère prometteuse et confirme que lorsqu’un modèle est présenté en tant que guide en plus d’être accompagné de stratégies, les élèves peuvent s’engager dans un processus de recherche plutôt que de suivre des étapes de façon systématique et séquentielle.

Bien qu’il y ait un lien à faire entre ces études et la question des modèles de résolution de problèmes présentés dans les classes, il est à noter que les modèles qui sont proposés dans ces recherches correspondent davantage à des modèles ayant été élaborés spécifiquement dans une visée d’enseignement de stratégies de résolution de problèmes. La question qui se pose maintenant est de savoir comment les modèles développés par la recherche sont introduits et utilisés au quotidien dans les classes du primaire. En d’autres mots, comment le passage de la théorie à la pratique est-il vécu au regard des modèles de résolution de problèmes mathématiques présentés aux élèves ?

Les modèles de résolution de problèmes développés par la recherche : passage de la théorie à la pratique

Le passage de la théorie à la pratique nécessite d’apporter une précision concernant le choix du vocabulaire à utiliser. En effet, étant donné la fonction qu’on leur accorde en classe, les modèles de résolution de problèmes mathématiques correspondent davantage à des méthodes. Par définition, un modèle est une représentation schématique ou symbolique d’un processus, d’une démarche raisonnée, ayant pour but de représenter une réalité, alors qu’une méthode est une séquence d’étapes agencées pour atteindre un but, pour parvenir à un résultat (Legendre, 2005). À la lumière de ces définitions, il devient évident qu’en contexte scolaire, les différentes étapes définies par les modèles ne sont pas utilisées pour représenter le processus de résolution de problèmes aux élèves : elles servent plutôt d’outils aidant les élèves à résoudre les problèmes proposés (but). Selon cette perspective, puisque nous traiterons maintenant des modèles utilisés dans les classes du primaire, le terme méthode sera désormais employé. Il est aussi important de préciser que l’objet d’étude est l’emploi de méthodes (au sens précédemment défini) et non l’emploi de stratégies, comme des stratégies cognitives ou métacognitives (planification, généralisation, régulation, etc.) (MELS, 2009).

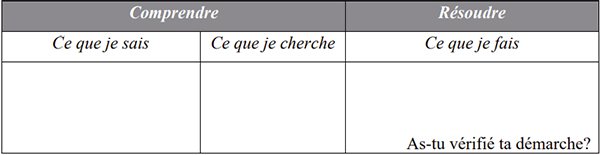
En consultant des manuels et cahiers d’exercices de mathématiques québécois destinés aux élèves du primaire, il est possible de constater que différentes maisons d’édition, telles que les éditions CEC et ERPI, présentent une méthode commune de résolution de problèmes, reconnue sous le nom de la méthode « ce que je sais, ce que je cherche ». La méthode comprend deux grandes étapes : comprendre et résoudre. L’étape de la compréhension est divisée en deux sections, « ce que je sais » et « ce que je cherche », alors que l’étape de la résolution comporte une seule section appelée « ce que je fais ».

La figure 1 illustre la méthode telle que présentée dans le cahier d’exercices Caméléon classe branchée 2e édition (2014) des éditions CEC, destiné aux élèves de quatrième année du primaire.

Figure 1

Méthode de résolution de problèmes mathématiques issue du cahier d’exercices Caméléon

Très peu d’écrits existent au sujet de cette méthode et de son utilisation. En fait, les seules informations disponibles sont celles fournies par les manuels et cahiers d’exercices de mathématiques. La façon dont la méthode est expliquée semble décrire un processus davantage séquentiel que cyclique, où les trois étapes doivent être vécues selon un ordre précis.

Problème de recherche et question générale

Considérant qu’il puisse y avoir une différence entre la méthode telle que décrite dans les manuels scolaires (qui semble inviter à un processus séquentiel axé sur le repérage) et sa transposition en classe par les enseignants, il y a lieu de se questionner sur la façon dont cette méthode est introduite dans les classes. En fait, cette observation permet de mettre en évidence que l’on ignore comment la méthode « ce que je sais, ce que je cherche » est présentée dans les classes puisqu’aucune donnée scientifique n’existe à son sujet, ni sur la façon dont elle est présentée par les enseignants ou utilisée par les élèves, ni sur les effets de son utilisation, et ce, malgré le fait qu’elle se retrouve dans les manuels et les cahiers d’exercices de mathématiques du primaire de la province du Québec. Plus fondamentalement, nous ignorons si la résolution de problèmes mathématiques telle qu’abordée en classe, notamment par l’entremise de la méthode « ce que je sais, ce que je cherche », se rapproche ou s’éloigne de l’atteinte des finalités de cette activité. Conséquemment, nous y voyons là un problème de l’ordre du manque de connaissances auquel nous avons décidé de nous attarder.

Selon cette perspective, nous posons la question générale de recherche suivante : « L’activité de résolution de problèmes mathématiques, lorsque présentée par l’entremise de la méthode “ce que je sais, ce que je cherche”, permet-elle l’atteinte des finalités associées à cette activité ? ». Pour bien comprendre cette question, il importe de préciser ce que nous entendons par résolution de problèmes mathématiques. Notre compréhension du concept de la résolution de problèmes cadre davantage avec la résolution de problèmes « en contexte scolaire », qui renvoie à un concept beaucoup plus large que celui défini par les écrits scientifiques. L’expression « résolution de problèmes mathématiques » est utilisée par les enseignants, dans les manuels scolaires, lors des évaluations des centres de services scolaires et du ministère ainsi que dans le Programme de formation de l’école québécoise (PFEQ). Autrement dit, dans la pratique, on parle de résolution de problèmes, même si inévitablement, il ne s’agira pas d’un véritable problème pour tous les élèves. En effet, le caractère relatif associé au concept de problème (Brun, 1990 ; Dionne, 1995 ; Fagnant et Demonty, 2004 ; Schoenfeld, 2014) rend très difficile, voire impossible, la possibilité de placer tous les élèves d’une même classe, ayant des connaissances et habiletés différentes, dans une véritable situation de résolution de problèmes. Conséquemment, dans le but de nous faire comprendre par les enseignants, nous avons choisi d’utiliser l’expression « résolution de problèmes mathématiques » telle qu’employée en contexte scolaire. Nous parlons plus précisément de « résolution de problèmes écrits de mathématiques ». Le mot « écrit » vise à préciser la forme sous laquelle les problèmes sont présentés. La définition retenue dans le cadre de notre étude est donc la suivante : « Un problème écrit de mathématiques renvoie à une description écrite d’une situation menant à une question mathématique pour laquelle l’élève doit mobiliser ses connaissances antérieures et établir différents liens en vue d’atteindre la solution ».

Puisque les connaissances actuelles dans la littérature scientifique à propos des méthodes de résolution de problèmes mathématiques présentées aux élèves du primaire sont encore limitées, alors que celles en lien avec la méthode « ce que je sais, ce que je cherche » sont pratiquement inexistantes, nous avons mené une première phase préliminaire qualitative en réalisant des entrevues auprès d’enseignants du primaire. Ce choix est justifié par notre visée de compréhension d’un objet d’étude relativement complexe et peu documenté au regard des pratiques des enseignants. La réalisation d’entrevues s’avérait donc être un bon choix pour mieux comprendre quelles sont les méthodes de résolution de problèmes utilisées dans les classes et comment celles-ci sont présentées aux élèves.

Cette phase préliminaire avait pour principal objectif de dégager les différents profils de pratiques relatives aux méthodes de résolution de problèmes écrits de mathématiques présentées aux élèves par les enseignants interrogés. Nous nous sommes aussi intéressés à savoir où se situent les pratiques déclarées des enseignants par rapport aux recommandations de la recherche. Un élément nous intéressait particulièrement, soit le respect du processus cyclique et itératif dans les méthodes de résolution de problèmes présentées aux élèves. Dix enseignants des 2^e et 3^e cycles du primaire (3^e-4^e-5^e-6^e année) issus de 10 écoles différentes ont pris part au processus d’entrevue. Ces enseignants travaillent pour trois centres de services scolaires différents des régions de Chaudière-Appalaches et de la Capitale-Nationale, et deux écoles primaires privées de la région de la Capitale-Nationale.

Bien que nous ne prétendions pas à la représentativité, les données obtenues lors de cette phase préliminaire nous amènent toutefois à soulever l’hypothèse générale selon laquelle la façon dont la méthode « ce que je sais, ce que je cherche » est présentée par les enseignants et utilisée par les élèves crée un écart entre ce que proposent la recherche et la pratique. En effet, si nous ignorons encore ce qui est fait par l’ensemble des enseignants, cette première tentative d’en savoir plus nous permet de constater que la majorité des enseignants rencontrés déclarent utiliser une méthode de type « ce que je sais, ce que je cherche », soit huit enseignants sur dix, alors que la position de ces huit enseignants au sujet de la façon de présenter les étapes d’une méthode de résolution de problèmes ne respecte pas le caractère cyclique et itératif qui devrait lui être associé. Plus précisément, des demandes faites aux élèves telles qu’une utilisation systématique et séquentielle des étapes présentées s’éloignent considérablement de ce qui est recommandé par la recherche. 

En somme, deux hypothèses spécifiques ont été formulées pour vérifier l’existence d’un écart entre la recherche et la pratique, à savoir :

• H.1. La majorité des enseignants utilisent dans leur classe la méthode « ce que je sais, ce que je cherche ».

• H.2. La méthode « ce que je sais, ce que je cherche » est davantage présentée de façon séquentielle que de façon cyclique et itérative.

À la lumière des données recueillies et des discussions menées auprès des enseignants interrogés, nous constatons plus précisément un manque de connaissances par rapport à la nature des pratiques enseignantes au regard des méthodes de résolution de problèmes écrits de mathématiques : le quoi (quelle méthode, ses avantages et ses inconvénients), le comment (quelles sont les exigences d’utilisation envers les élèves) et le pourquoi (quelles sont les raisons) de l’utilisation d’une méthode en particulier.

Pour combler ce manque de connaissances et pour vérifier nos hypothèses, nous avons formulé l’objectif suivant : décrire les pratiques relatives aux méthodes de résolution de problèmes écrits de mathématiques présentées par les enseignants des deuxième et troisième cycles du primaire. Ce choix de travailler auprès des enseignants de ces deux cycles a été fait dans une visée de cohérence avec la phase préliminaire. À cet objectif sont associées deux questions principales et quatre sous-questions, telles que présentées dans la figure ci-dessous :

Figure 2

Questions et sous-questions de recherche

Méthodologie

La littérature rapporte que le développement d’instruments fiables et valides permettant de décrire l’enseignement vécu en classe constitue un défi méthodologique, et ce, quel que soit le type de méthode choisie (Ball et Rowan, 2004). Cependant, plusieurs auteurs soutiennent que les limites associées aux méthodes de recherche quantitative et qualitative dans ce domaine d’étude en particulier peuvent être minimisées par l’utilisation d’un devis mixte (Hiebert et Grouws, 2007 ; Maxwell, 2004). Sans prétendre que nous avons eu recours à une approche mixte en soi, nous pouvons toutefois affirmer qu’un volet qualitatif, réalisé par l’intermédiaire des entrevues de la phase préliminaire, a servi d’appui au volet quantitatif envisagé pour la présente phase. En effet, les entrevues nous ont permis d’obtenir des descriptions détaillées des différentes pratiques privilégiées en classe pour travailler la résolution de problèmes écrits de mathématiques, ce qui a ensuite été mis à profit pour l’élaboration des questionnaires, qui constituent l’instrument de collecte de données retenu pour la phase présentée dans le présent article. Concrètement, l’analyse des données qualitatives nous a amenés, d’une part, à être attentifs aux incompréhensions des enseignants occasionnées par certains choix de mots, et d’autre part, à utiliser leur témoignage pour bâtir les choix de réponses présentés dans le questionnaire. Par exemple, l’analyse de contenu des verbatim issus des entrevues nous a amenés à définir différents profils chez les enseignants interrogés concernant la présentation d’une méthode de résolution de problèmes écrits de mathématiques. Les quatre profils ayant émergé des analyses se distinguent par la flexibilité de l’enseignant quant à l’utilisation systématique ou non de l’ensemble des étapes de la méthode présentée et par l’ordre de réalisation, étant soit imposée séquentiellement ou non. Les profils sont présentés dans la figure suivante :

Figure 3

Profils d’utilisation d’une méthode de résolution de problèmes des enseignants de la phase préliminaire

À la suite de la phase préliminaire, un questionnaire électronique autoadministré en ligne a été utilisé. Ce choix est justifié par le fait qu’il s’agit d’une façon rapide de recueillir des données d’un grand échantillon réparti sur un vaste territoire (Fortin et Gagnon, 2022). De plus, l’utilisation de questionnaires afin d’obtenir des données au sujet de ce que les enseignants font dans leur classe constitue une pratique méthodologique grandement répandue parmi les études quantitatives recensées (Desimone et al., 2010 ; Fagnant et Burton, 2009 ; Lubienski, 2006). Afin de construire ce questionnaire, nous avons repris la majorité des questions issues du canevas d’entrevue, que nous avons adaptées pour en faire (le plus souvent possible) des questions semi-structurées ou fermées. Une pré-expérimentation a été réalisée auprès d’enseignants de la population cible. Finalement, 143 enseignants du deuxième et du troisième cycle ont rempli notre questionnaire via le logiciel de sondage en ligne SurveyMonkey. 

Les données issues des questionnaires autoadministrés ont été traitées au moyen d’analyses descriptives. Ces analyses ont permis de décrire les différents items du questionnaire, dans le but de brosser un portrait général des pratiques d’enseignement relatives à la résolution de problèmes écrits de mathématiques. Par ailleurs, les deux questions ouvertes du questionnaire ont été traitées quantitativement et qualitativement : les réponses ont été catégorisées pour ensuite en établir les fréquences.

Principaux résultats relatifs aux pratiques déclarées des enseignants

Pour ce qui est de la question 1 « Quelles sont les pratiques déclarées des enseignants au regard de la présentation d’une méthode de résolution de problèmes écrits de mathématiques et de leurs exigences relatives à l’utilisation qui en est faite par les élèves ? », il faut noter que les enseignants ont d’abord été questionnés à savoir s’ils utilisaient une méthode ou non pour travailler la résolution de problèmes avec leurs élèves. Les résultats montrent clairement que les enseignants des deuxième et troisième cycles du primaire présentent une séquence à suivre afin de résoudre les problèmes écrits de mathématiques proposés dans leur classe (98,4 %). Seulement deux enseignants ont déclaré « Ne pas enseigner de séquence à suivre », ce qui représente moins de 2 % de l’échantillon. Les données obtenues rapportent plus précisément que les enseignants se répartissent de façon pratiquement équivalente entre les trois autres profils A, B et C (présentés précédemment).

À la suite de cette première question plus générale, nous avons vérifié parmi les 143 enseignants combien d’entre eux utilisent une méthode de type « ce que je sais, ce que je cherche » dans leur classe. Les résultats obtenus permettent de confirmer nos deux hypothèses de recherche. Concernant l’hypothèse 1, la popularité de la méthode « ce que je sais, ce que je cherche » dans les classes des deuxième et troisième cycles du primaire des quatre centres de services scolaires de la région de Chaudière-Appalaches est confirmée : 90,8 % des enseignants ayant répondu au questionnaire en ligne déclarent utiliser une telle méthode dans leur classe.

Pour ce qui est de la deuxième hypothèse, selon laquelle la méthode « ce que je sais, ce que je cherche » est davantage présentée de façon séquentielle que de façon cyclique et itérative, 99,1 % des enseignants utilisant cette méthode ont déclaré la présenter selon une séquence à suivre, alors que 33,6 % exigent plus précisément que leurs élèves réalisent toutes les étapes, selon l’ordre présenté (profil A). Conséquemment, au lieu de promouvoir le développement d’habiletés de résolution de problèmes, une telle pratique favorise plutôt le développement d’habiletés liées à la mémorisation et à l’application d’étapes (imposées aux élèves). Nous considérons ce résultat comme un premier élément basé sur des données scientifiques témoignant d’un écart entre ce que propose la recherche et ce qui est vécu dans la pratique. Il importe cependant de souligner que ce n’est pas la méthode en soi qui crée un écart entre la recherche et la pratique, mais bien la façon dont celle-ci est utilisée. Plus précisément, l’écart serait créé par le fait d’imposer l’utilisation systématique d’une méthode séquentielle, comme la méthode de type « ce que je sais, ce que je cherche ».

Du point de vue des enseignants, l’utilisation de la méthode « ce que je sais, ce que je cherche » serait majoritairement justifiée par l’aide qu’elle procure aux élèves alors que 63,1 % des enseignants ont déclaré utiliser cette méthode d’abord parce qu’ils pensent qu’elle aide les élèves à mieux comprendre et/ou à résoudre le problème correctement. Les données en lien avec les avantages perçus par les enseignants ont permis de préciser qu’ils y voient principalement une aide à l’organisation (« Offrir une structure aux élèves pour les aider à organiser leur travail étape par étape »). Cet avantage rapporté par plus de 60 % des répondants laisse croire que les enseignants valorisent la résolution de problèmes séquentielle, ce qui vient appuyer une seconde fois l’existence d’un écart entre la recherche et la pratique. Les données ont aussi montré que 27 % des enseignants, soit plus du quart des répondants, utilisent cette méthode non pas par choix, mais par obligation. Plus précisément, 10,8 % des enseignants ont déclaré utiliser cette méthode parce qu’il s’agit de celle proposée dans le manuel ou le cahier d’exercices mathématiques qu’ils utilisent, alors que 9 % l’utilisent parce que cette méthode leur est imposée par leur direction ou leur centre de services scolaire. Ces données quantitatives, combinées aux données qualitatives issues de la phase préliminaire, permettent de mieux comprendre la situation dans laquelle certains enseignants se trouvent. Les propos d’un enseignant rencontré lors des entrevues sont présentés dans la figure ci-dessous pour témoigner du fait que l’utilisation de la méthode « ce que je sais, ce que je cherche » devient inévitable pour certains enseignants.

Figure 4

Verbatim issus de l’entrevue : échange entre l’enseignant A et la chercheuse

L’échange entre cet enseignant et la chercheuse permet de comprendre que cette méthode est introduite très tôt dans les classes, ce qui fait en sorte que les enseignants des deuxième et troisième cycles sont appelés à travailler avec des élèves qui associent depuis déjà deux, trois ou quatre ans la résolution de problèmes mathématiques à la méthode « ce que je sais, ce que je cherche ».

Finalement, en ce qui a trait aux inconvénients perçus par les enseignants, les données montrent que 18 % n’y voient aucun inconvénient, alors que l’inconvénient le plus souvent rapporté est celui de l’inutilité pour certains élèves (36 %). Il faut aussi souligner que 36,9 % des enseignants, correspondant à plus du tiers des répondants, ont déclaré reconnaître des inconvénients plus sérieux, au sens où ceux-ci sont nuisibles pour les élèves (découragement (ex. : baisse de motivation, perte d’intérêt) et des sources de confusion chez les élèves (occasionner un deuxième problème)). Par ailleurs, les données qualitatives issues des entrevues menées lors de la phase préliminaire de l’étude nous apprennent que certains enseignants considèrent même que la méthode puisse nuire à l’efficacité de leurs élèves à résoudre les problèmes. Les propos ci-dessous (figure 5), tenus par trois enseignants différents, en sont de bons exemples :

Figure 5

Verbatim issus de l’entrevue : exemples de propos d’enseignants

De tels résultats vont dans le même sens que nos hypothèses de recherche liées aux conséquences possibles pouvant être associées à l’existence d’un écart, question ayant fait l’objet d’une autre publication (voir Goulet-Lyle et al. 2020).

En réponse à notre deuxième question de recherche « Quelle est la perspective des enseignants sur les finalités de la résolution de problèmes écrits de mathématiques ? », l’ensemble des données recueillies suggèrent que les enseignants ne semblent pas conscients de la double finalité associée à l’activité de résolution de problèmes en contexte scolaire. Toutefois, il faut noter que cette conclusion repose sur une interprétation réalisée sans avoir pu obtenir de précisions de la part des enseignants par rapport aux propos (écrits) déclarés. En effet, le choix de notre instrument de collecte de données, soit un questionnaire autoadministré en ligne, nous amène à devoir vivre avec une interprétation limitée des réponses des enseignants. Conséquemment, nous pensons qu’il est plus approprié de formuler notre conclusion sous la forme d’une question et d’une hypothèse. Les enseignants sont-ils au courant qu’ils devraient travailler la résolution de problèmes en tant qu’objet d’étude, mais aussi en tant qu’approche pédagogique ? Sur les bases de notre analyse, nous soulevons l’hypothèse selon laquelle les enseignants ne sont pas au fait de cette double finalité, et conséquemment, nous doutons aussi que les deux finalités soient travaillées dans les classes du primaire. Des entrevues semi-dirigées auprès des enseignants permettraient de leur demander clairement s’ils connaissent les finalités associées à l’activité de résolution de problèmes mathématiques (À quoi sert selon eux l’activité de résolution de problèmes ?). Des échanges portant sur leur opinion par rapport à la double finalité et à ce qu’ils en pensent nous permettraient de mieux comprendre si et comment ces finalités sont intégrées à leur pratique.

Discussion

À l’instar des résultats obtenus, nous sommes d’avis que l’activité de résolution de problèmes mathématiques serait souvent réduite à l’enseignement d’une méthode. Ce constat émane du fait que le tiers des enseignants ayant pris part au projet de recherche ont déclaré présenter une séquence de résolution de problèmes que leurs élèves doivent utiliser, et ce, en respectant deux exigences : (1) compléter chacune des étapes de la méthode et (2) procéder selon l’ordre prescrit. En d’autres mots, dans le tiers des classes, une méthode de résolution de problèmes est imposée aux élèves : ces derniers doivent utiliser la méthode choisie par leur enseignant pour résoudre les problèmes auxquels ils font face. L’accent est donc mis sur l’apprentissage d’une méthode plutôt que sur l’apprentissage d’habiletés de résolution de problèmes. 

Il est important de rappeler que les méthodes de résolution de problèmes devraient être présentées aux élèves en tant que ressources (générales) pouvant les aider à aborder les problèmes, dans le sens de les outiller à faire des choix éclairés en tant que solutionneur autonome (ministère de l’Éducation de l’Ontario, 2006 ; Pólya, 1945 ; Reys et al., 2012). D’ailleurs, le MELS (2006) explique que dans la pratique, le processus de résolution de problèmes devrait être souple (retours en arrière/va-et-vient), raisonné et contrôlé. En réduisant la résolution de problèmes à l’enseignement, l’apprentissage et l’application d’une méthode unique, il serait surprenant que les élèves associent la résolution de problèmes à un processus de recherche itératif à propos duquel ils ont le contrôle. Les chances qu’ils considèrent la résolution de problèmes comme étant simplement une série d’étapes à suivre sont beaucoup plus grandes. C’est d’ailleurs ce qu’ont montré les résultats du questionnaire d’opinion réalisé lors de la phase 3 de notre étude : 84,6 % des élèves ont déclaré être d’accord avec l’affirmation « Résoudre un problème écrit de mathématiques, c’est suivre des étapes dans un ordre bien précis » (Goulet, 2018).

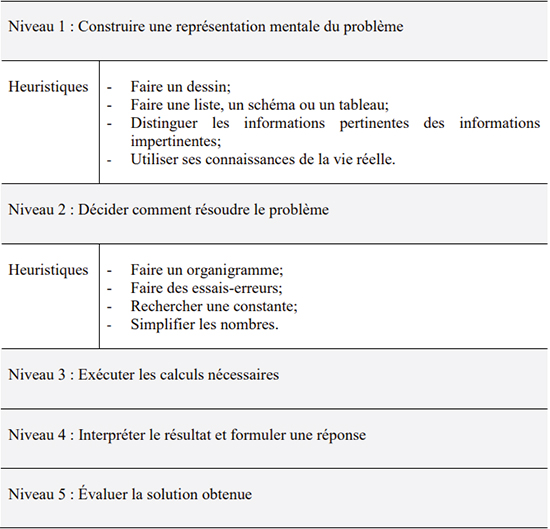
Par ailleurs, le fait d’imposer une méthode peut entraîner un comportement passif de la part des élèves lorsqu’ils sont appelés à résoudre des problèmes, notamment à l’égard des stratégies métacognitives mises en oeuvre. De ce fait, les élèves deviendraient davantage des exécuteurs que des solutionneurs. À l’opposé, le modèle compétent de résolution de problèmes mathématiques développé par Verschaffel et son équipe (1999) constitue un exemple concret permettant de former les élèves à devenir des solutionneurs plus engagés, plus motivés et plus stratégiques (figure 6).

Figure 6

Modèle compétent de résolution de problèmes de Verschaffel et al. (1999)

Si l’on compare cette stratégie générale de résolution de problèmes à la méthode « ce que je sais, ce que je cherche », il est possible d’établir des liens étroits. La section « ce que je sais » peut être comparée au niveau 1 de la stratégie de Verschaffel et al. (1999) « Construire une représentation mentale du problème », alors que la section « ce que je cherche » peut être comparée au niveau 2 « Décider comment résoudre le problème ». Ces deux premiers niveaux sont à notre avis des versions améliorées des sections « ce que je sais » et « ce que je cherche ». Alors qu’actuellement, les élèves recopient les informations repérées dans le texte (Goulet et Voyer, à paraître), ceux-ci devraient être formés à se créer une représentation mentale de la situation dans laquelle s’inscrit le problème. Sachant aussi que les élèves sélectionnent généralement des données inutiles et oublient des données utiles (Goulet et Voyer, 2023), la stratégie spécifique « distinguer les informations pertinentes des informations impertinentes » intégrée dans le modèle compétent de Verschaffel et al. (1999) mériterait d’être présentée aux élèves. En somme, la méthode « ce que je sais, ce que je cherche » pourrait permettre aux élèves de devenir de bons solutionneurs si celle-ci était utilisée différemment. Les sections « ce que je sais » et « ce que je cherche » sont celles nécessitant des changements majeurs.

Conclusion

L’hypothèse selon laquelle la majorité des enseignants des deuxième et troisième cycles du primaire ne semblent pas au fait de la double finalité associée à l’activité de résolution de problèmes n’est pas surprenante, considérant que les moyens pour atteindre ces finalités ne sont pas explicités dans le PFEQ, qui pourtant devrait servir de document de référence pour les enseignants. Quel éclairage est fourni aux enseignants québécois (du primaire et du secondaire) pour aborder la résolution de problèmes avec les élèves ? Cette question a été soulevée par Lajoie et Bednarz (2014) qui ont mené une étude au sujet de l’évolution des rôles assignés à la résolution de problèmes par les programmes et des conseils donnés aux enseignants pour atteindre les finalités prescrites. À la suite d’une analyse des différents documents officiels québécois (MEQ, 2001 ; MELS, 2003, 2005), les auteures concluent notamment que :

Les conseils aux enseignants au regard de la résolution de SP (situation-problème) sont souvent formulés de manière indirecte. Dans les programmes du primaire et du début du secondaire (MEQ, 2001 ; MELS, 2003), par exemple, ces conseils sont difficiles à repérer, puisqu’ils ne sont pas formulés explicitement. Qui plus est, ils ne sont pas regroupés dans une même section

Lajoie et Bednarz, 2014, p. 14

Si ces auteures parlent plus spécifiquement du concept de SP en mathématiques, il en va de même pour l’activité de résolution de problèmes au sens large. Les enseignants interrogés dans le cadre de notre phase préliminaire nous ont expliqué que les SP ne font pas partie de leur enseignement quotidien de la résolution de problèmes, mais sont plutôt travaillées en fin d’étape pour préparer les élèves aux évaluations du centre de services scolaire (ou du ministère pour le troisième cycle). Ainsi, quotidiennement, on s’attend à ce que les enseignants abordent la résolution de problèmes en tant qu’habileté (finalité objet d’étude), mais aussi en tant que contexte (finalité approche pédagogique) sans leur fournir de piste quant à la façon dont ces deux finalités peuvent s’articuler concrètement auprès des élèves. Quels types de problèmes peuvent favoriser l’atteinte de ces deux finalités ? Faut-il travailler les deux finalités séparément ? Comment peut se vivre une séance de résolution de problèmes pour introduire un nouveau concept mathématique ? Quel est le rôle des élèves et celui de l’enseignant ? Ces questions étant actuellement sans réponse pour les enseignants, des mesures devront être prises par les acteurs du milieu de l’éducation afin de mieux former les enseignants québécois au regard du double rôle de la résolution de problèmes en mathématiques, mais aussi concernant le rôle qui leur revient en tant qu’enseignant. Cette même problématique a été soulevée par Lester (1994) qui affirme que les enseignants doivent se contenter d’une banque bien intentionnée de problèmes à résoudre, d’une liste de stratégies à enseigner et de suggestions d’activités de classes, plutôt que d’avoir accès à un programme avec des directives claires quant à la façon de faire de la résolution de problèmes une partie intégrante du curriculum. Le problème décrit par Lester en 1994 nous apparaît encore à ce jour d’actualité, du moins, pour le programme du Québec.