Analyse de la relation entre le revenu et la mortalité : un commentaire méthodologique

Finès, Philippe; Wilkins, Russell; Courteau, Jean-Pierre; Berthelot, Jean-Marie

doi:https://doi.org/10.7202/019493ar

Introduction

La région métropolitaine de recensement (RMR) d’Ottawa-Gatineau est unique au Canada. C’est la seule RMR à cheval sur deux provinces. Ses deux composantes (Ottawa en Ontario et Gatineau au Québec) sont intimement reliées au niveau économique et social; elles sont cependant très différentes sur le plan des indicateurs de revenu et de santé. Le fait que Gatineau puisse être considérée comme faisant à la fois partie de cette RMR et du Québec urbain accorde à cette ville une position particulière : selon la référence à laquelle elle est comparée, cette ville présente des indicateurs contradictoires ou au contraire cohérents.

Il existe un lien entre le statut socio-économique et la santé. Cette relation – qui peut être analysée spécifiquement en termes de revenus et d’espérance de vie – est décrite abondamment dans la littérature. D’une part, une distribution inégale des revenus va en général de pair avec une mortalité élevée (Wolfson et al., 1999; Ross, 2004; Wilkinson et Pickett, 2006), d’autre part, des revenus plus élevés sont associés à une mortalité plus basse (Courteau et Trempe, 1996; Wilkins et al., 2002). Or, Courteau et Trempe (1996) ont montré que cette dernière relation n’est pas réalisée pour Gatineau : dans ce qu’ils appellent le « paradoxe outaouais », ils montrent que, bien que les habitants de cette ville jouissent d’un statut socio-économique supérieur à la moyenne observée pour le Québec urbain, les indicateurs de mortalité y sont au contraire plus défavorables. Une cause possible de ce paradoxe serait que les résidents de Gatineau, malgré leur revenu relativement élevé par rapport au reste du Québec, n’ont peut-être pas un « sentiment de contrôle sur [leur] vie » (Courteau et Trempe, 1996). En plus de décrire ce paradoxe, les auteurs proposent une hypothèse permettant de l’élucider : selon eux, il serait plus approprié d’analyser les résultats concernant Gatineau en tenant compte du fait qu’elle constitue une partie de la région métropolitaine de recensement (RMR) d’Ottawa-Gatineau. Dans cette perspective, le paradoxe se résoudrait : « L’Outaouais urbain constituant en fait un sous-ensemble “pauvre” d’une agglomération urbaine, il n’est pas surprenant qu’il ait des indicateurs de santé moins bons » (Courteau et Trempe, 1996).

Nous nous proposons dans cet article de prendre le relais de Courteau et Trempe. En utilisant le même support théorique qu’eux sur des données plus récentes (à savoir, le recensement de 1996[1]), nous voulons vérifier si l’explication proposée par ces auteurs s’avère juste. En fait, nous utiliserons ce cas pour illustrer à quel point l’analyse de la relation entre le revenu et la mortalité dépend des choix méthodologiques, lorsque l’unité analysée (ici, Gatineau) fait partie d’un ensemble de référence qui peut être déterminé de plusieurs manières. Notre propos portera sur la manière dont cette relation varie selon, d’un côté, le choix de l’ensemble de référence et, de l’autre, la définition des quintiles de revenu.

Données et méthodologie

Données et calcul des indicateurs de mortalité

Il s’agit tout d’abord de calculer les taux de mortalité par sexe, unité d’analyse et quintile de revenu (ces deux derniers concepts étant décrits plus loin). Pour cela, nous avons construit des tables de mortalité en utilisant les vingt strates d’âge suivantes : < 1 an, 1-4 ans, 5-9 ans, 10-14 ans,... jusqu’à 90 ans et plus. Nous avons calculé les numérateurs en cumulant les décès pour les années 1994 à 1998 (sauf pour les données concernant Ottawa qui sont cumulées de 1996 à 1998) à partir des registres d’état-civil et avons attribué le secteur de recensement des personnes décédées à partir de leur code postal (Wilkins, 2002). Pour calculer les dénominateurs (années-personnes à risque), nous avons multiplié les tailles de populations provenant du recensement de 1996 (en excluant les personnes vivant en institution de santé) par le nombre d’années durant lesquelles les décès ont été comptés. Les personnes vivant en institution de santé ont aussi été exclues des numérateurs. Pour la mortalité des personnes âgées de 85 ans et plus, nous avons attribué aux cinq quintiles de revenu les taux de mortalité observés pour les quintiles regroupés.

À partir des tables de mortalité, nous avons calculé les indicateurs de mortalité suivants :

l’espérance de vie à la naissance, avec la méthode de Chiang (1984);
le taux de mortalité standardisé, en utilisant comme population de référence celle du Canada en 1991 (sexes confondus);
le taux d’années potentielles de vie perdues avant 75 ans (Wilkins et al., 2002).

Comparaison entre villes

Dans un premier temps, la mise en évidence du paradoxe évoqué plus haut consiste à examiner la relation entre un indicateur de richesse et un indicateur de mortalité entre villes. Pour ce faire, nous comparerons les unités d’analyse suivantes : Gatineau; Ottawa; la RMR Ottawa-Gatineau dans son ensemble; le Québec urbain, constitué de tous les secteurs de recensement des six RMR du Québec (Montréal, Québec, Sherbrooke, Trois-Rivières et la partie québécoise d’Ottawa-Gatineau).

Pour décrire le niveau de revenu global d’une unité d’analyse, nous avons utilisé trois indicateurs de revenu : le revenu individuel moyen; le revenu individuel médian; le pourcentage d’individus vivant sous le seuil de faible revenu. Ce seuil est déterminé par Statistique Canada et dépend de la taille de la ville considérée et de la taille de la famille. A titre d’exemple, mentionnons que pour une ville d’au moins 500 000 habitants en 1996, il valait 31 753 $ par an pour une famille de quatre personnes et 42 978 $ par an pour une famille de sept personnes ou plus (Statistique Canada, 1999). Pour décrire la mortalité d’une unité d’analyse, nous avons utilisé les trois indicateurs de mortalité mentionnés plus haut.

Comparaison entre quartiers

Dans un deuxième temps, au niveau des quartiers à l’intérieur d’une ville, la relation entre le revenu et la mortalité s’exprime en termes de quintiles : on s’attend à ce que le quintile le plus riche ait un meilleur indicateur de santé que le quintile suivant, lui-même en meilleure santé que le troisième, et ainsi de suite. Cette série de valeurs prend la forme d’un gradient.

Construction du gradient

Cette méthode a déjà été utilisée ailleurs (Wilkins et al., 1989; Wilkins et al., 2002; James et al., 2007) :

On définit les quartiers d’une ville (ou d’une RMR); dans notre étude, il s’agit des secteurs de recensement.
On définit un indicateur décrivant le niveau de revenu dans chacune de ces composantes; nous avons utilisé le pourcentage de personnes vivant sous le seuil de faible revenu.
On trie ensuite la liste des composantes de la ville par ordre croissant de l’indicateur du niveau de revenu. Les secteurs de recensement situés en haut de la liste contiennent le plus faible pourcentage de personnes « pauvres », ce sont donc les secteurs de recensement les plus « riches »; ceux qui sont situés en bas étant les plus « pauvres ». On divise cette liste triée en cinq quintiles, de telle manière que chaque quintile contienne (approximativement) 20 % des individus de la ville (« approximativement » 20 % car on ne coupe pas en deux un secteur de recensement).
Une partition est représentée par l’ensemble des quatre seuils qui définissent les quintiles de revenus d’une ville donnée.

Pour Ottawa et Gatineau, nous avons utilisé deux types de partitions. Dans un premier temps, étant donné que notre objectif était d’analyser Gatineau à l’intérieur de sa RMR, nous avons défini pour cette unité d’analyse une « partition commune » en triant dans une liste commune les secteurs de recensement appartenant à toute la RMR, selon le même indicateur du pourcentage de personnes vivant sous le seuil de faible revenu.

Cependant, puisque Gatineau est – de manière générale – plus pauvre qu’Ottawa, le premier quintile obtenu avec la partition commune est surtout composé de secteurs de recensement provenant d’Ottawa. Par conséquent, afin d’analyser chacune des deux rives de la RMR comme si elle était une entité autonome, nous avons également défini une partition pour chacune des deux rives séparées à partir des secteurs de recensement propres à chacune d’elles. Nous obtenons ainsi des « partitions propres ». Par symétrie, il est également possible d’analyser, d’une part, chacune des deux rives selon les partitions communes et, d’autre part, la RMR en entier selon les partitions propres.

En ce qui concerne le Québec urbain, la partition choisie est obtenue à partir du regroupement quintile par quintile des partitions propres à chaque RMR. À des fins de comparaison, rappelons ici que, dans l’étude précédente concernant les données de 1986, Courteau et Trempe (1996) avaient trié dans une seule liste tous les secteurs de recensement des six RMR du Québec urbain (selon le même indicateur du pourcentage d’individus vivant sous le seuil de faible revenu). Cette liste a été divisée en cinq quintiles de revenu selon une partition que nous nommons « partition provinciale » pour la distinguer des autres partitions.
Enfin, pour chaque unité d’analyse et chaque sexe, l’indice de mortalité désiré (dans cette étude, c’est l’espérance de vie) a été calculé pour les cinq quintiles de la partition considérée.

Test de « significativité » statistique d’un gradient

Nous proposons la méthode suivante pour déterminer si le gradient de l’espérance de vie (pour une unité d’analyse et un sexe donnés) est (statistiquement) significatif. Pour simplifier, nous ne tenons compte que des quintiles de rang 1, 3 et 5. Considérons les deux inégalités suivantes :

espérance de vie de Q1 supérieure à l’espérance de vie de Q3 (1a),
espérance de vie de Q3 supérieure à l’espérance de vie de Q5 (1b).

La « significativité » statistique de chaque inégalité (1a) et (1b) est établie par le calcul d’un rapport critique, dont le numérateur est égal à la différence entre l’espérance de vie des deux quintiles impliqués, et dont le dénominateur est égal à la racine carrée de la somme des carrés des erreurs-types des deux espérances de vie. On compare ce rapport critique à la valeur critique 1.955 (qui est obtenue à partir de la valeur critique de la distribution normale, lorsque le niveau α = 5 % se trouve d’un seul côté, et lorsque l’on a appliqué la correction de Bonferroni pour deux comparaisons simultanées). Si les deux inégalités sont significatives, nous dirons alors que le gradient est significatif.

Résultats

Distributions des populations selon les partitions choisies

Le tableau 1 indique les partitions et les proportions observées dans les unités d’analyse, selon chacune des définitions. On observe qu’avec la partition commune, le quintile 1 (le plus riche) est sous-représenté à Gatineau (10,4 %) alors que ce n’est pas le cas avec la partition propre à Gatineau (22,4 %). Simultanément, à Ottawa, la part représentée par le quintile 1 passe de 25,2 % (partition commune) à 20,3 % (partition propre à Ottawa). Ces deux phénomènes s’expliquent par l’examen des seuils définissant le premier quintile : le pourcentage de personnes vivant sous le seuil de faible revenu varie entre 1,1 et 6,7 % pour la partition commune, entre 1,1 et 5,8 % pour la partition propre d’Ottawa et entre 5,2 et 10,6 % pour la partition propre de Gatineau. Comme les secteurs de recensement ayant les plus faibles pourcentages se trouvent surtout à Ottawa, la contribution de Gatineau au premier quintile est (sensiblement) plus faible que 20 % (pourcentage que l’on aurait réalisé si les deux villes contribuaient également au premier quintile). Avec les partitions propres, le premier quintile de Gatineau a une borne supérieure plus élevée que pour la partition commune (10,6 % au lieu de 6,7 %) – ce qui permet d’obtenir (environ) 20 % de la population totale de Gatineau – alors que le 1^er quintile d’Ottawa a une borne supérieure moins élevée que dans le cas précédent.

Tableau 1

Seuils ayant servi à la détermination des quintiles de revenu, Ottawa-Gatineau, Ottawa, Gatineau et le Québec urbain en 1996, de même que le Québec urbain en 1986 (pourcentages de population vivant en ménage privé sous le seuil de faible revenu)

Remarquons que c’est à Ottawa que l’on trouve les deux quartiers de la RMR les plus pauvres (en termes de proportions de personnes vivant sous le seuil de faible revenu) : cela explique en partie pourquoi le quintile le plus pauvre est relativement plus populeux à Ottawa (20,4 % selon la partition commune) qu’à Gatineau (18,3 % selon la partition commune). On constate également que, pour Gatineau en 1986, la proportion de sa population appartenant au premier quintile provincial était de 26 % (= 51 410 197 970) en 1986, alors que 12 % seulement se trouvait dans le quintile le plus pauvre : cette année-là aussi, Gatineau était plus riche que le reste du Québec.

Impact du choix de l’ensemble de référence : analyse du « paradoxe outaouais »

Le tableau 2 comprend les valeurs des principaux indicateurs de mortalité, de même que les trois indicateurs de revenu choisis. Il permet d’examiner la relation entre le revenu et la mortalité, au niveau de la ville.

Tableau 2

**Indicateurs de mortalité et indicateurs de revenu pour le Québec urbain, Gatineau, Ottawa, et Ottawa-Gatineau, 1996**

En comparant les colonnes « Gatineau » et « Québec urbain », on met en évidence le paradoxe. En effet, d’une part, Gatineau a un revenu plus élevé que celui du Québec urbain entier (l’ensemble des RMR du Québec) selon les trois indicateurs de revenu choisis. D’autre part, ses indicateurs de mortalité sont en général plus défavorables (la seule exception étant pour les années potentielles de vie perdues, ce qui pourrait être dû à une structure d’âge différente entre ces unités d’analyse). En examinant les intervalles de confiance, on remarque que l’espérance de vie à la naissance est significativement inférieure (à 95 %) à celle du Québec urbain, tant pour les hommes que pour les femmes. Cette différence d’au moins une demi-année représente un écart appréciable. De même, les deux taux de mortalité standardisés (hommes et femmes) de Gatineau sont significativement supérieurs à ceux du Québec urbain.

En utilisant maintenant la colonne « Ottawa-Gatineau » comme élément de comparaison pour la colonne « Gatineau », on fait disparaître le paradoxe. On observe que le revenu de Gatineau est moins élevé que celui de la RMR, et les indicateurs de mortalité y sont tous statistiquement plus défavorables. En particulier, l’espérance de vie à la naissance est inférieure d’au moins une année (tant pour les hommes que pour les femmes) par rapport à la RMR, ce qui indique à quel point Gatineau est la « banlieue pauvre » d’Ottawa (Courteau et Trempe, 1996). À titre indicatif, nous avons indiqué en dernière colonne du tableau 2 les résultats concernant Ottawa seule.

Impact du mode de définition des quintiles de revenu

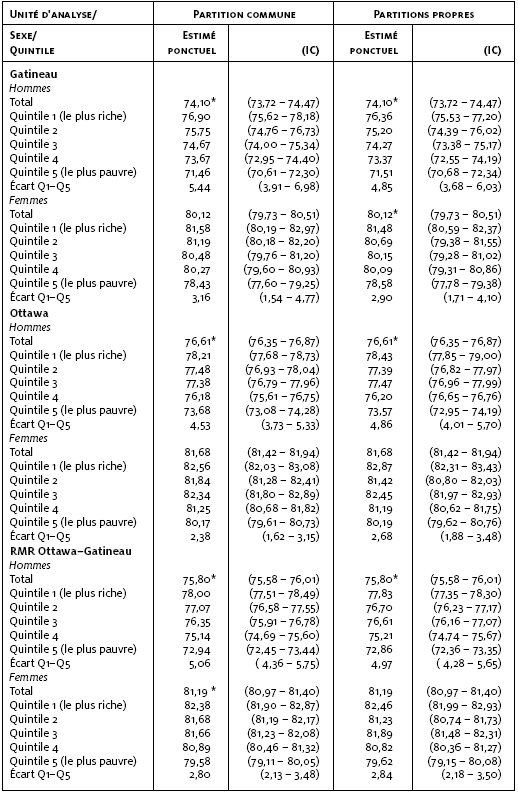
Les tableaux 3A et 3B permettent de comparer le gradient de Gatineau à ceux, d’un côté, de la RMR Ottawa-Gatineau [tableau 3A], et de l’autre, du Québec urbain [tableau 3b]. Remarquons en premier lieu que, dans chaque quintile, on retrouve les écarts que nous avions notés entre Gatineau et les deux autres unités d’analyse.

Tableau 3

A

**Espérance de vie à la naissance selon le quintile de revenu et le sexe, écarts entre les quintiles, pour Gatineau, Ottawa et Ottawa-Gatineau, partitions commune et propres, 1996**

B

**Espérance de vie à la naissance selon le quintile de revenu et le sexe, écarts entre les quintiles pour le Québec urbain, 1996**

-> See the list of tables

En utilisant la partition commune établie pour l’ensemble de la RMR, on obtient une image artificiellement embellie de la réalité (pour le quintile le plus riche). Rappelons en effet (voir tableau 1) que, lorsque l’on utilise cette partition, le premier quintile représente seulement 10 % de la population de Gatineau. Le tableau 3A montre, chez les hommes de ce quintile, une différence d’un peu plus d’une année entre Ottawa et Gatineau (78,21 – 76,90 = 1,31), même en utilisant cette sélection pour Gatineau. Avec une partition propre à Gatineau, on passe maintenant de 10 % à 22 % de la population pour le premier quintile, ce qui entraîne une diminution de l’espérance de vie de ce quintile (étant donné que – de façon imagée – on ajoute des individus « plus pauvres », qui vivent donc moins longtemps). En même temps, à Ottawa, l’utilisation de la partition propre au lieu de la partition commune fait passer le poids du premier quintile de 25 % à 20 %, ce qui résulte en une augmentation de l’espérance de vie de ce quintile (puisqu’on en retranche les individus « les plus pauvres »). Ces deux effets se combinent pour amplifier l’écart entre les deux villes de l’espérance de vie du quintile le plus riche : celui-ci devient maintenant supérieur à deux années (78,43 – 76,36 = 2,07). On observe le même phénomène chez les femmes, mais à un degré moindre : la différence passe de 0,98 (= 82,56 – 81,58) à 1,39 (= 82,87 – 81,48).

L’ampleur de l’écart entre quintiles extrêmes (Q1 et Q5) de même que la « significativité » statistique du gradient d’une unité d’analyse donnée varient également en fonction de la partition choisie (tableau 3a). Avec la partition propre, le gradient de Gatineau est significatif pour les hommes et pour les femmes (l’écart vaut respectivement 4,85 et 2,90 années); avec la partition commune, le gradient de Gatineau est significatif seulement pour les hommes (l’écart vaut 5,44 chez les hommes et 3,16 chez les femmes). Pour Ottawa, seul le gradient des hommes est significatif, quelle que soit la partition utilisée (écart = 4,53 avec la partition commune et 4,86 avec la partition propre); chez les femmes, l’écart est de l’ordre de 2,5 années. Pour la RMR, le gradient des hommes et le gradient des femmes sont tous deux significatifs avec la partition commune (écart = 5,06 chez les hommes et 2,80 chez les femmes); avec la partition propre, seul le gradient des hommes est significatif (écart = 4,97), mais pas celui des femmes (écart = 2,84). Enfin, pour le Québec urbain (tableau 3b), le gradient des hommes et celui des femmes sont tous deux significatifs avec la partition utilisée (écart = 4,66 chez les hommes et 2,13 chez les femmes).

Discussion

Nous avons pu montrer que lorsque l’unité de référence est choisie de différentes manières, les résultats sont sujets à varier. Premièrement, au niveau de la ville, la relation revenu-mortalité peut être préservée ou inversée (sous la forme du paradoxe) en fonction du choix de l’unité de référence. Deuxièmement, au niveau des quintiles de la ville, le choix de la partition modifie l’écart entre quintiles extrêmes (de plus d’une demi-année chez les hommes de Gatineau). Troisièmement, le choix de la partition peut également affecter la « significativité » statistique du gradient.

Tous ces faits permettent d’illustrer que, dans le cas où plusieurs options sont possibles, les choix méthodologiques concernant l’unité de référence et la partition sont importants. Ce ne sont évidemment pas les résultats qui devraient orienter ces choix. Au contraire, ceux-ci devraient être déterminés a priori, en fonction du plan de recherche adopté par l’analyste.

Revenons à la situation de Gatineau. L’analyste doit d’abord choisir s’il veut comparer Gatineau au Québec urbain ou à la RMR Ottawa-Gatineau. Dans ce dernier cas, il doit ensuite décider s’il examine chacune des deux rives séparément ou s’il analyse la RMR comme une entité insécable. Les deux types de partitions répondent à deux problématiques différentes. En utilisant des partitions propres, l’analyste privilégie la comparabilité entre rives et considère chacune d’elles comme une ville autonome. Les résultats ainsi obtenus permettent de donner des indications en termes de politiques (approche « décideur »). Par contre, en utilisant une partition commune, on traduit davantage l’approche « usager » du fait que chacun des résidents de chaque rive a, dans une certaine mesure, le choix de traverser ou non la rivière des Outaouais.

Cette étude est de nature partiellement écologique au sens de Björk et Strömberg (2005) : l’« exposition » (le revenu du quartier) est agrégée et les autres variables sont individuelles. Par conséquent, cette étude ne permet pas d’établir une relation directe entre le revenu de l’individu et son niveau de santé. Il reste que les approximations que nous avons utilisées conviennent pour nos besoins. En particulier, le revenu du quartier est un bon indicateur du revenu des ménages qui y habitent : les familles sont portées à résider dans des quartiers dans lesquels elles ont les moyens financiers de vivre. De leur côté, les indicateurs basés sur la mortalité sont des indicateurs objectifs de la santé. Cependant, le concept de qualité de vie n’est pas pris en compte dans cette étude : les indicateurs d’espérance de vie ajustés pour les incapacités n’ont pas été considérés.

Bien que la relation entre le statut socio-économique et la santé soit décrite en termes d’indicateurs de mortalité, d’indicateurs de revenu et de quintiles de revenu, les résultats qui la décrivent sont fiables. Ainsi, en examinant pour Gatineau deux niveaux de la relation entre le revenu et la mortalité (ville et quartiers), nous avons été en mesure de montrer que lorsque l’on peut choisir l’unité de référence, les choix méthodologiques ont un impact important dans l’estimation et l’interprétation des résultats de toute analyse portant sur cette relation.

Analyse de la relation entre le revenu et la mortalité : un commentaire méthodologiqueAnalysing the relationship between income and mortality : a methodological comment

Résumé

Abstract

Introduction

Données et méthodologie