Abstracts
Résumé
Dans cet article, j’exploite l’approche développée par Beaulieu, Dufour et Khalaf (2013, 2017) pour montrer comment une méthode robuste aux problèmes d’identification et correcte en échantillons finis peut être utilisée afin d’identifier les facteurs à incorporer dans un modèle d’évaluation d’actifs dans le but de mieux estimer le prix du risque. En fait, lorsque l’incertitude entourant les paramètres du modèle du calcul du prix du risque est importante, elle peut changer de façon significative les décisions d’investissement et de financement. L’approche développée par Beaulieu, Dufour et Khalaf (2013, 2017) permet d’établir conjointement si un modèle est rejeté ou non et s’il est identifié ou non. Trois cadres d’analyse mesurant le prix du risque sont comparés.
Article body
Introduction
La base de la décision de l’investissement et du financement dépend directement du prix du risque. Ce dernier est défini comme la sensibilité du rendement d’un actif au changement dans le bêta[1] d’un facteur, c’est-à-dire la part des fluctuations du rendement des actifs due au changement dans la part du risque systématique liée à un facteur donné. Les mesures financières de ce risque sont déployées le plus souvent dans les modèles d’évaluation d’actifs dont le plus connu est le Capital Asset Pricing Model (CAPM). Depuis son développement dans les années 1960, les assises empiriques de ce modèle ont été remises en question à plusieurs reprises nommément depuis les travaux de Fama et French (1992, 1993), ces derniers ouvrant la porte à un débat récurrent dans les travaux empiriques : quels facteurs doit-on inclure dans nos modèles?
Pris ensemble, les modèles d’évaluation d’actifs servent à calculer le coût du capital d’un projet en fonction du prix du risque. Dans la forme classique du CAPM, on utilise la somme du taux sans risque et de la prime de risque multipliée par le bêta d’une firme pour mesurer le coût d’opportunité d’investir dans un projet plutôt que dans un autre ou encore on utilise ce même coût d’opportunité pour motiver le choix d’un mode de financement plutôt qu’un autre. L’importance de ce coût dans les modèles d’affaires est connue et enseignée depuis longtemps. Les travaux récents de Gollier (2016) montrent comment cette question de mesure du coût du capital est importante quand on en vient à qualifier le choix d’un projet qu’il soit de nature sociale ou complètement entrepreneuriale. Gollier (2016) reprend le vieux dilemme de l’allocation intertemporelle optimale des ressources lorsque l’horizon d’investissement dépasse l’espérance de vie d’un agent représentatif.
Un élément clé dans la mesure du prix du risque concerne l’incertitude entourant les paramètres du modèle du calcul du coût du capital. En sa présence, les décisions d’investissement peuvent être influencées même dans un cadre très simple où les décisions de financement et d’investissement sont sur un horizon très court. Les problèmes d’identification liés à cette imprécision se traduisent souvent non pas par un rejet du modèle mais plutôt par une validation du modèle pour n’importe quelle valeur de l’ensemble des réels. Cette situation pose des problèmes d’implémentation puisque le calcul du coût du capital implique souvent les coûts minimal et maximal pour un décideur. Si l’intervalle de confiance de ce coût n’est pas borné, il en résulte une prise de décision pas plus informée à l’aide des données que dans l’ignorance du coût du capital à proprement parler. L’approche développée par Beaulieu, Dufour et Khalaf (2013, 2017) permet de mettre en lumière ces modèles non rejetés mais mal identifiés afin d’informer le décideur de l’incertitude entourant les paramètres du modèle et d’ainsi en arriver ultimement à des mesures plus utiles et mieux comprises du coût du capital.
De façon stricte, un modèle est identifié lorsqu’il est possible d’en tirer une inférence à partir de la distribution des probabilités des variables observées qui sont liées à une structure théorique latente (Dufour et Hsiao, 2008). Dans ce cas, un modèle bien identifié au sens statistique est un modèle pour lequel les données relatent des informations fiables quant aux paramètres estimés. Dans les modèles d’évaluation d’actifs, deux traits qui leur sont relatifs peuvent miner l’identification du modèle, soit : (i) les facteurs redondants c’est-à-dire des bêtas ou encore des combinaisons linéaires des bêtas proches de zéro, et (ii) le regroupement dit clustering, c’est-à-dire, les bêtas qui ne diffèrent que de peu à l’intérieur d’un groupe d’actifs testés, qui sont par exemple, près de un.
Pour les raisons invoquées en introduction, l’identification est un problème sérieux puisque dans un modèle mal identifié, les intervalles de confiance de type Wald utilisés traditionnellement ne couvriront pas avec les probabilités désirables[2] les valeurs appropriées des coefficients et les tests qui y sont associés sur-rejetteront les hypothèses nulles (Dufour, 1997; Beaulieu, Dufour et Khalaf, 2013; Gospodinov, Kan et Robotti, 2013; Kan, Robotti et Shanken, 2013; Kleibergen et Zhan, 2015; Khalaf et Schaller, 2016). Les intervalles de confiance de type Wald ou Student sont des intervalles de la forme : {estimé ± (erreur type) × point critique}. Quand l’identification n’est pas respectée, les estimés sont biaisés et les erreurs types sous-estiment sévèrement l’incertitude de l’estimation, et ce, même lorsque les échantillons sont de grande taille.
La littérature financière, depuis les travaux de Merton (1973) et ceux de Ross (1976), reconnaît la valeur de facteurs autres que celui du marché pour évaluer les actifs, soit dans un contexte intertemporel ou encore d’extraction de facteurs. Cependant, c’est depuis les articles de Fama et French (1992 et 1993) que les travaux de recherche se sont ouverts fermement à l’idée que l’introduction de facteurs supplémentaires au rendement du portefeuille de marché est importante pour la qualité des modèles d’évaluation d’actifs. Cependant, tel que souligné par Campbell, Liu et Zhu (2016), les chercheurs ont mis de l’avant quelque 314 facteurs au cours des 20 dernières années pouvant expliquer les rendements boursiers. Dans le but de sélectionner les facteurs les plus importants, Campbell, Liu et Zhu prêchent pour une approche basée sur un cadre de tests multiples et une statistique significative lorsqu’elle est plus élevée que 3,0. Le choix des facteurs à inclure dans un modèle économique est un problème important dans les études empiriques et l’approche présentée ici développe un critère nécessaire mais non suffisant dans la recherche du meilleur modèle d’évaluation d’actifs empirique à valider.
Le test inversé, développé par Beaulieu, Dufour et Khalaf (2013) représente une approche valide pour évaluer les facteurs à inclure pour l’obtention d’un modèle identifié. Il s’agit de la seule méthode disponible robuste aux problèmes d’identification définis plus haut et correcte en échantillons finis. Les ensembles de confiance (par opposition aux intervalles de confiance de type Wald) couvrent la vraie valeur des paramètres estimés avec le niveau désiré, que l’identification pose problème ou non.
1. Modèle d’évaluation d’actifs et évidence empirique
Le modèle du CAPM développé par Treynor (1961, 1962), Sharpe (1964), Lintner (1965) et Mossin (1966) repose sur le principe de la diversification de portefeuille et lie
Dans ce contexte, l’estimation du bêta (βi) est un enjeu important qui puise à même la relation risque–rendement révélant la hauteur de la sensibilité d’un actif au risque de marché.
Ce modèle a mené aux premiers tests d’évaluation d’actifs qui furent développés en coupe transversale par Black, Jensen et Scholes (1972), Fama et MacBeth (1973) et Blume et Friend (1973). Pour une discussion plus récente des forces, faiblesses et défis relatifs à cette approche, voir Lewellen, Nagel et Shanken (2010).
En coupe transversale, on cherche à établir si le bêta du facteur est important statistiquement à travers un grand nombre d’actifs. Pour ce faire, le modèle estimé est le suivant :
Le test du modèle afin d’estimer l’importance du bêta à travers un ensemble de titres financiers revient alors à valider :
Dans cette première approche pour tester l’équation (1) en coupe transversale, on cherche donc à savoir si à travers différents portefeuilles d’actifs, le bêta de ces portefeuilles varie suffisamment pour que le prix du facteur de risque justifie qu’on lui attribue un prix au sens statistique.
Bien que très intuitive, cette approche pose a priori que les βi soient connus alors qu’empiriquement, ils doivent être estimés dans une première étape en utilisant par exemple le modèle donné par l’équation (1), impliquant des erreurs de mesure. La formation de portefeuilles pour mesurer la variable endogène dans le but de regrouper les actifs vise à minimiser l’impact de ces erreurs de mesure sur les estimés des βi.
Par ailleurs, l’estimation des modèles d’évaluation d’actifs fait une nouvelle avancée lorsque Jensen (1968) introduit l’idée de tester la performance d’actifs en séries chronologiques. Cette idée est reprise par Gibbons (1982) qui teste, à partir du modèle suivant :
l’hypothèse nulle
Cette démarche vise à valider l’hypothèse de l’efficience moyenne-variance du portefeuille de marché. Le non-rejet de cette hypothèse nulle implique que le modèle du CAPM à un facteur est suffisant pour expliquer la variance du rendement des actifs.
MacKinlay (1985) et Gibbons, Ross et Shanken (1989) exploiteront l’approche développée par Gibbons afin de rendre l’inférence robuste aux échantillons finis lorsque l’hypothèse de normalité des résidus est retenue. Beaulieu, Dufour et Khalaf (2007) présentent l’inférence relative à un test qui généralise l’évidence de MacKinlay (1985) et Gibbons, Ross et Shanken (1989) de la même hypothèse de l’efficience moyenne–variance en échantillons finis à des classes de distributions elliptiques.
Par ailleurs, l’arbitragepricing theory (APT) développée par Ross (1976) mène à des tests de modèles qui impliquent que plusieurs composantes communes et spécifiques peuvent affecter l’évaluation d’actifs. La version empirique de cette approche généralise à plusieurs facteurs le modèle du CAPM tel que décrit à l’équation (1) sous condition que les facteurs soient indépendants les uns des autres ainsi que des termes d’erreur. Le modèle de l’APT implique donc la possibilité que plus d’un facteur soit nécessaire pour expliquer les rendements boursiers. La forme générale empirique de ce modèle est la suivante :
Si ce modèle justifie l’introduction de facteurs dans un modèle d’évaluation d’actifs, puisque ces facteurs s’associent à une extraction par composante principale et qu’ils permettent d’identifier combien de facteurs sont utiles pour l’évaluation d’actifs, il rend l’interprétation économique de ces mêmes facteurs difficiles puisque les facteurs ne sont pas donnés a priori mais plutôt extraits des variations dans les rendements boursiers en utilisant des combinaisons des régresseurs indépendants les uns des autres. Puisque ces facteurs sont en essence générés par les données, il s’avère impossible de les connaître ex ante et encore plus de les associer à des variables économiques précises.
Finalement, les travaux de Merton (1973) permettent également de mettre en valeur un modèle d’évaluation d’actifs à plusieurs facteurs qui représentent les changements dans l’espace moyenne-variance des titres accessibles à l’investisseur. Si ce modèle intertemporel prévoit l’introduction de facteurs supplémentaires au modèle empirique, il demeure imprécis quant à quels facteurs inclure au modèle d’évaluation d’actifs.
Ce sont les travaux de Fama et French (1992 et 1993) qui marquent l’ouverture de la profession à l’idée que le modèle du CAPM à un facteur ne suffit pas à modéliser les variations empiriques des rendements financiers. Débute alors un courant de recherche qui vise à identifier des facteurs basés dans un premier temps sur les caractéristiques des firmes mais qui s’ouvrira plus largement dans les années suivantes.
On pensait déjà à des facteurs macroéconomiques (Chen, Roll et Ross, 1986), mais la littérature se transporte très rapidement sur des facteurs d’autre nature dont les facteurs comportementaux (facteurs psychologiques dont l’instinct grégaire) ou encore des facteurs de microstructure (par exemple, Pastor et Stambaugh, 2003). Cependant dans la mesure où les facteurs sont extraits des données tel que proposé par l’APT ou encore choisis de manière plus ou moins ad hoc, les modèles théoriques nous sont jusqu’à maintenant d’un support modeste. À ce stade, seule une procédure statistique rigoureuse peut nous être utile puisque tel que discuté en introduction, étant donné le recensement de Campbell et al., la question qui demeure et qui en soi dépasse celle posée par les modèles d’évaluation d’actifs est : quels facteurs et combien? L’idée d’un test conjoint sur une hypothèse donnée et l’identification d’un modèle fournissent un outil permettant de mieux cerner la réponse à cette question.
2. Cadre méthodologique
Le modèle d’évaluation d’actifs le moins contraint[3] auquel on peut penser prend la forme suivante :
Le modèle de l’équation (5) est une représentation en séries chronologiques d’une interprétation en coupe transversale suivant la restriction développée par Shanken et Zhou (2007) pour estimer la coupe transversale en une seule étape.
Si l’on reprend l’équation (5) en permettant la distinction entre les facteurs R selon leur nature, le modèle présenté à l’équation (6) inclut des facteurs négociables en bourse (R1) et des facteurs non négociables en bourse (F). De plus, pour modéliser la prime de risque, on mesure dans une première étape les rendements endogènes et les facteurs en déviation par rapport au taux zéro-bêta (γ0) dans le cas des actifs négociables en bourse ou au rendement attendu de chaque facteur (γ'F) si celui-ci n’est pas négociable en bourse. Dans l’ensemble, le modèle prend la forme suivante :
Empiriquement, l’estimation mais surtout l’inférence à partir de ce modèle impliquent des défis importants puisqu’il se trouve qu’ici, γ0 et γF sont non observables, de même que bi1 et biF. Étant donné que seulement R1 et F sont observables du côté droit de l’équation (6), nous expliquons plus bas comment cette difficulté sera contournée. Par ailleurs, à noter que le prix du risque ici correspond toujours au coefficient sur les différents bi1 et biF qui s’exprime dans ce nouveau modèle non plus par λ comme à la section 2, mais plutôt par R1 – γ0 et F – ɩTγ'F.
Dans un contexte encore plus général, il est également possible de relâcher empiriquement l’hypothèse que γ0 soit le même des deux côtés de l’équation (6), c’est-à-dire que dans le cas des portefeuilles étudiés et du portefeuille de marché, ceux-ci ne seraient pas mesurés en excédant de la même mesure, soit le rendement du portefeuille à zéro-bêta. Si c’était le cas, c’est-à-dire que le gamma soit le même de chaque côté de l’équation (6) pour les facteurs négociés en bourse et le rendement des actifs à l’étude, alors l’évidence empirique serait cohérente avec le modèle théorique.
Afin de s’en tenir à l’estimation du modèle présenté à l’équation (5), qui ne comporte pas les mêmes défis que l’estimation du modèle présenté à l’équation (6), on peut réécrire l’équation (6) comme l’équation (5), en lui imposant la restriction non linéaire suivante :
Empiriquement, afin de valider l’adéquation de l’équation (6), nous testons l’équation (7) qui constitue notre hypothèse nulle. Celle-ci dépend à la fois de γ0 et de γF ainsi que des bêtas qui sont traités comme inconnus, nous permettant d’éviter des erreurs de mesure liés à leur estimation. À noter qu’une caractéristique importante de notre approche est le traitement conjoint des facteurs de façon simultanée plutôt que par étapes subséquentes.
Pour tester la significativité du prix du risque des différents facteurs à l’étude, nous effectuons des tests simultanés afin d’évaluer si les ensembles de confiance robustes à l’identification (CS) de γ0 et de γ'F recoupent la moyenne de R1 et de F. Précisons que nous nous concentrons sur la moyenne des facteurs afin d’évaluer la significativité du prix du risque des facteurs parce que lorsque l’équation (6) est réexprimée en moyenne, les coefficients ![]() et
et ![]() sont ceux que l’on obtient dans une régression en coupe transversale classique.
sont ceux que l’on obtient dans une régression en coupe transversale classique.
Ainsi, si la moyenne du facteur est recoupée par l’intervalle de confiance, le prix du risque du facteur n’est pas significatif et ce facteur n’apporte rien au sens statistique au modèle d’évaluation d’actifs.
Une démarche classique viserait plutôt la formation d’un intervalle de confiance de type Wald qui aurait la forme {valeur estimée ± (erreur type asymptotique) X (point critique asymptotique)}. Dans l’approche développée par Beaulieu, Dufour et Khalaf (2013, 2017) nous utilisons notre hypothèse nulle pour inverser une statistique de Hotelling T 2 et retenons les valeurs de γ0 et de γ'F dans l’intervalle de confiance conjoint qui sont cohérentes avec l’hypothèse nulle. L’approche utilisée ici est une généralisation de Beaulieu, Dufour et Khalaf (2013) dans un cadre multidimensionnel tel que développée dans Beaulieu, Dufour et Khalaf (2017).
Afin de présenter la statistique développée dans Beaulieu, Dufour et Khalaf (2013), il faut d’abord présenter le modèle de régression (5) dans un contexte général où Y = XB + U. Empiriquement, nous aurons ![]() où
où ![]()
On définit également :
pour lesquelles la statistique[4] est définie par
Comme il est démontré dans Beaulieu, Dufour et Khalaf (2013), lorsque les erreurs sont normales,
Plus généralement, pour inverser la statistique, nous devons résoudre
qui produit un intervalle de confiance conjoint pour θ et ϕ avec un seuil de confiance α découlant d’une généralisation multidimensionnelle d’une solution analytique proposée par Beaulieu, Dufour et Khalaf (2013) et présentée dans Beaulieu, Dufour et Khalaf (2017). Les ensembles de confiance individuels de θ et ϕ ainsi obtenus le sont par le biais des projections de la région de confiance conjointe. Notez que Beaulieu, Dufour et Khalaf (2017) montrent par simulations que les résultats sont robustes à des déviations à l’hypothèse de normalité.
L’interprétation liée aux intervalles de confiance obtenus sont de quatre natures différentes. Dans un premier cas, les intervalles de confiance sont bornés impliquant que les facteurs du modèle sont informatifs et que le modèle en soi ne pose pas de problème d’identification. Dans un deuxième cas, les intervalles de confiance sont non bornés ce qui implique que les facteurs sont informatifs, mais qu’il faut se soucier des problèmes d’identification du modèle. Dans le troisième cas où l’intervalle de confiance comprend l’ensemble des réels, nous sommes en présence de problèmes d’identification sévère du modèle, bien que les facteurs apparaissent toujours pertinents. Finalement, dans le quatrième cas, les intervalles de confiance sont vides et le modèle est rejeté par les données, révélant ainsi que les facteurs ne sont pas adéquats et n’aident pas à évaluer les actifs.
L’avantage de l’approche développée par Beaulieu, Dufour et Khalaf (2013) est que plutôt que de se contraindre à un intervalle de confiance classique basé sur une mesure de l’écart-type par rapport à la moyenne du paramètre qui, en présence de problèmes d’identification, se révèle fallacieux, nous proposons l’inversion de la statistique qui caractérise l’hypothèse nulle du modèle en fonction de toutes les valeurs possibles des paramètres. Cette approche donne de l’information simultanée sur (i) le modèle, (ii) son identification et (iii) sa spécification.
Afin d’illustrer l’évidence présentée par cette approche dans différents contextes, j’introduis dans la prochaine section des résultats en provenance de trois études différentes, soit : (i) l’évaluation du prix du risque de divers facteurs dans l’économie américaine tirés de Beaulieu, Dufour et Khalaf (2017), (ii) du prix du risque des obligations catastrophes tirés de Beaulieu, Khalaf et Melin (2017) et (iii) du prix du risque de facteurs domestiques et internationaux dans le but de tester l’intégration des marchés financiers à l’international en provenance de l’étude de Beaulieu, Gagnon et Khalaf (2016).
3. Études empiriques
Afin de mieux comprendre les avantages de l’approche développée par Beaulieu, Dufour et Khalaf (2013 et 2017), je propose ici de comparer trois cadres d’analyse utilisant des actifs financiers dans trois contextes différents. Cet exercice permet d’apprécier le type de résultats obtenus et de voir si certaines questions de recherche se prêtent davantage à l’utilisation de cette approche ou non.
3.1 Économie américaine
La première étude empirique discutée ici est celle de Beaulieu, Dufour et Khalaf (2017). Il s’agit de mesurer la significativité du prix du risque du modèle à trois facteurs de Fama et French pour l’ensemble des titres américains regroupés en 12 portefeuilles triés par industrie. La période échantillonnée s’étend de janvier 1961 à décembre 2010 et l’ensemble des données pour les portefeuilles triés par industrie ainsi que pour le rendement du portefeuille de marché (MKT), le facteur de taille (SMB) et celui du ratio de valeur au livre sur valeur au marché (HML) sont tirés du site de Kenneth French. Les résultats sont présentés en sous-périodes de 10 ans afin de préserver des séries relativement homogènes et non sujettes à des changements structurels importants.
Le modèle estimé si l’on contraint le même rendement excédentaire pour les facteurs négociables en bourse est le suivant :
Par ailleurs, le modèle peut être estimé dans une forme plus large suivant :
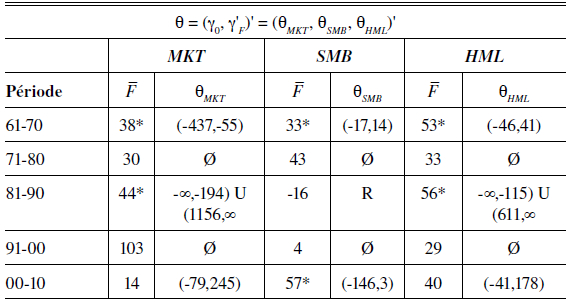
Les résultats obtenus pour l’estimation de ces deux modèles sont présentés dans les tableaux 1 et 2. Au tableau 1, lorsque le modèle est estimé en excès du rendement zéro-bêta comme à l’équation (11), sur des sous-périodes de 10 ans, les résultats montrent que sur la première sous-période, allant de 1961 à 1970, les 3 facteurs de Fama-French, soit le rendement du portefeuille de marché (MKT), le facteur de taille (SMB) et celui de valeur (HML), sont bien identifiés étant donné que les ensembles de confiance sont fermés. Les facteurs apparaissent tous significativement différents de 0 puisque la moyenne de chacun de ces facteurs n’est pas incluse dans leur ensemble de confiance respectif. Le modèle est rejeté pendant la sous-période suivante et celle de 1991 à 2000, les résultats montrant qu’aucune valeur de θ n’est compatible avec l’hypothèse nulle. Finalement, la sous-période 2000 à 2010 révèle des ensembles de confiance bornés mais recouvrant la moyenne du facteur dans 2 cas sur 3, montrant peu de pouvoir explicatif pour ces 2 facteurs.
Tableau 1
Économie américaine
Intervalles de confiance du prix du risque des trois facteurs de Fama-French
Note : Ce tableau présente  la moyenne de chaque facteur du modèle d’évaluation d’actifs pour l’ensemble de l’économie américaine ainsi que l’ensemble de confiance obtenu par l’inversion de la statistique de Hotelling. Les données incluent 12 portefeuilles industrie pour le vecteur de variables endogènes ainsi que les facteurs de i) marché, ii) taille, iii) valeur au livre sur valeur de marché, toutes tirées du site de Kenneth French allant de 1961 à 2010. Voir Beaulieu, Dufour et Khalaf (2017) pour l’ensemble des détails concernant les données. Les prix du risque significatifs à un seuil de 5 % sont représentés par un astérisque.
la moyenne de chaque facteur du modèle d’évaluation d’actifs pour l’ensemble de l’économie américaine ainsi que l’ensemble de confiance obtenu par l’inversion de la statistique de Hotelling. Les données incluent 12 portefeuilles industrie pour le vecteur de variables endogènes ainsi que les facteurs de i) marché, ii) taille, iii) valeur au livre sur valeur de marché, toutes tirées du site de Kenneth French allant de 1961 à 2010. Voir Beaulieu, Dufour et Khalaf (2017) pour l’ensemble des détails concernant les données. Les prix du risque significatifs à un seuil de 5 % sont représentés par un astérisque.
Au tableau 2, lorsque le rendement zéro-bêta peut différer des deux côtés de l’équation comme à l’équation (12), l’évidence en faveur du facteur de marché est très forte sur toutes les sous-périodes sauf la dernière montrant que les facteurs de taille et de valeur n’ont pas de pouvoir explicatif. Cette évidence ouvre la porte à une autre vision du modèle du CAPM qui serait plus performant lorsque l’on permet aux rendements endogènes et au facteur négocié en bourse d’être mesurés en excédant de quantités qui peuvent différer empiriquement.
Tableau 2
Économie américaine
Intervalles de confiance du prix du risque des trois facteurs de Fama-French
Note : Ce tableau présente  la moyenne de chaque facteur du modèle d’évaluation d’actifs pour l’ensemble de l’économie américaine ainsi que l’intervalle de confiance obtenu par l’inversion de la statistique de Hotelling dans le cas où les rendements du portefeuille de marché et des rendements endogènes ne sont pas pour la même mesure excédentaire. Les données incluent 12 portefeuilles industrie pour le vecteur de variables endogènes ainsi que les facteurs de i) marché, ii) taille, iii) valeur au livre sur valeur de marché, toutes tirées du site de Kenneth French allant de 1961 à 2010. Voir Beaulieu, Dufour et Khalaf (2017) pour l’ensemble des détails concernant les données. Les prix du risque significatifs à un seuil de 5 % sont représentés par un astérisque.
la moyenne de chaque facteur du modèle d’évaluation d’actifs pour l’ensemble de l’économie américaine ainsi que l’intervalle de confiance obtenu par l’inversion de la statistique de Hotelling dans le cas où les rendements du portefeuille de marché et des rendements endogènes ne sont pas pour la même mesure excédentaire. Les données incluent 12 portefeuilles industrie pour le vecteur de variables endogènes ainsi que les facteurs de i) marché, ii) taille, iii) valeur au livre sur valeur de marché, toutes tirées du site de Kenneth French allant de 1961 à 2010. Voir Beaulieu, Dufour et Khalaf (2017) pour l’ensemble des détails concernant les données. Les prix du risque significatifs à un seuil de 5 % sont représentés par un astérisque.
3.2 Obligations catastrophe
Les résultats de cette section sont tirés de l’article de Beaulieu, Khalaf et Melin (2017) qui traite de l’analyse empirique des obligations catastrophe. De par leur nature, ces obligations devraient être des actifs à zéro-bêta, c’est-à-dire que ces obligations ne devraient pas avoir un prix du risque significativement différent de zéro pour n’importe quel facteur de risque donné (Cummins et Weiss, 2009). Si ces actifs sont effectivement à zéro-bêta, ils présentent donc un potentiel de diversification important pour les investisseurs.
Dans ce contexte, le modèle contraint estimé dans sa forme la plus large est le suivant :
Un facteur de risque correspondant au rendement du portefeuille de marché est un facteur qui capture l’asymétrie du rendement du marché, tel que développé dans le modèle de Kraus et Litzenberger (1976). Il s’agit de déterminer ici si le prix du risque du portefeuille de marché et du facteur d’asymétrie recoupent leur moyenne échantillonné afin de convenir s’il s’agit de facteurs importants à travers différents fonds mutuels d’obligations catastrophe. Notez que Cummins et Weiss (2009) testent la même hypothèse pour une période échantillonnée différente et avec un test valide seulement asymptotiquement sans contrôle pour les problèmes d’identification potentiels.
Les rendements quotidiens des fonds mutuels d’obligations catastrophe sont évalués entre novembre 2004 et août 2014 et sont extraits de Bloomberg. Le facteur de marché provient du site de Kenneth French. Les détails sur les données sont fournis dans Beaulieu, Khalaf et Melin (2017).
Empiriquement, nous considérons l’ensemble de la période échantillonnée disponible allant de novembre 2004 à août 2014 mais aussi trois sous-périodes couvrant les mois précédant, pendant et suivant la récession associée à la crise financière de 2008, soit une première sous-période (sous-période 1) allant de novembre 2004 à novembre 2007, une seconde sous-période (sous-période 2) allant de décembre 2007 à mai 2009 et une dernière sous-période (sous-période 3) allant de juin 2009 à août 2014.
Les résultats présentés au tableau 3 montrent que sur l’ensemble de la période échantillonnée, le facteur de marché (MKT) n’est pas identifié mais que le facteur d’asymétrie est statistiquement important et relativement bien identifié. Cela peut apparaître surprenant dans la mesure où ces actifs présentent en principe un prix du risque nul pour tout facteur. Aussi, l’évidence en sous-période est-elle importante pour mieux cerner les explications à ce résultat. Dans un premier temps, les résultats sur le prix du risque de la première sous-période montrent que le modèle estimé est clairement rejeté par les données. En fait, aucune valeur du prix du risque du facteur de marché ou du facteur d’asymétrie n’est compatible avec les données. Ceci est bien conforme à nos attentes puisque les obligations catastrophe sont en principe insensibles à tout facteur de risque. Pendant la seconde sous-période, soit au plus fort de la crise financière de 2008, les deux prix du risque sont identifiés et statistiquement importants pour expliquer les rendements des obligations castastrophe. Pendant la troisième sous-période, le prix du risque du facteur de marché n’est pas identifié alors que c’est le cas pour le facteur d’asymétrie qui est par ailleurs statistiquement significatif. Cette évidence suggère qu’en période d’acalmie, les obligations catastrophe sont effectivement insensibles aux facteurs de risque usuels mais qu’en période de crise, elles ne comportent pas la diversification attendue par les détenteurs de ces obligations.
Tableau 3
Obligations catastrophe
Intervalles de confiance du prix du risque des facteurs du CAPM asymétrique
Note : Ce tableau présente  la moyenne de chaque facteur du modèle d’évaluation d’actifs pour l’ensemble des obligations catastrophe ainsi que l’ensemble de confiance obtenu par l’inversion de la statistique de Hotelling pour chacun des facteurs nommément le rendement du portefeuille de marché et le rendement du portefeuille de marché au carré. On rapporte l’intervalle de confiance obtenu pour le prix du facteur de risque. Les facteurs de risque sont le rendement du portefeuille de marché et le rendement du portefeuille de marché au carré suivant le modèle du CAPM asymétrique (Kraus et Litzenberger, 1976) Sur la première ligne de chaque cellule les intervalles de confiance présentés sont obtenus par l’inversion de la statistique de Hotelling présentée à l’équation (8) et l’intervalle de confiance présenté à la ligne suivante est obtenu par la statistique Wald classique. La variable endogène est le rendement des fonds mutuels catastrophes tirés de Bloomberg. Voir Beaulieu, Khalaf et Melin (2017) pour plus de détails. Les prix du risque significatifs à un seuil de 5 % sont représentés par un astérisque.
la moyenne de chaque facteur du modèle d’évaluation d’actifs pour l’ensemble des obligations catastrophe ainsi que l’ensemble de confiance obtenu par l’inversion de la statistique de Hotelling pour chacun des facteurs nommément le rendement du portefeuille de marché et le rendement du portefeuille de marché au carré. On rapporte l’intervalle de confiance obtenu pour le prix du facteur de risque. Les facteurs de risque sont le rendement du portefeuille de marché et le rendement du portefeuille de marché au carré suivant le modèle du CAPM asymétrique (Kraus et Litzenberger, 1976) Sur la première ligne de chaque cellule les intervalles de confiance présentés sont obtenus par l’inversion de la statistique de Hotelling présentée à l’équation (8) et l’intervalle de confiance présenté à la ligne suivante est obtenu par la statistique Wald classique. La variable endogène est le rendement des fonds mutuels catastrophes tirés de Bloomberg. Voir Beaulieu, Khalaf et Melin (2017) pour plus de détails. Les prix du risque significatifs à un seuil de 5 % sont représentés par un astérisque.
3.3 Économie internationale
Dans cette dernière partie, je discute une partie des résultats de Beaulieu, Gagnon et Khalaf (2016) afin de montrer comment, dans un contexte international, le nombre de facteurs domestiques et globaux peuvent exacerber les problèmes d’identification puisque dans une économie partiellement intégrée, on devra tenir compte de la double nature (domestique et internationale) des facteurs du modèle d’évaluation d’actifs.
Dans ce contexte, le modèle international, intégrant des facteurs globaux et domestiques définis par leur prix du risque sont les suivants :
Le modèle dans ce contexte est défini comme suit :
L’analyse empirique utilise un échantillon allant de 1987 à 2011 pour les modèles internationaux. Les portefeuilles analysés sont les rendements de tous les titres canadiens listés en bourse sur la même période et les facteurs globaux, incluant le rendement du portefeuille de marché (MKT), le facteur de taille (SMB), le facteur du ratio valeur au livre sur valeur de marché (HML) et le facteur de momentum (MOM) sont tirés du site de Kenneth French. Les facteurs domestiques qui pour notre exemple sont canadiens, sont construits suivant la même démarche que Fama et French (1993) avec des données extraites de Worldscope. Le rendement des facteurs domestiques est orthogonalisé avec son homologue global suivant la démarche décrite dans Beaulieu, Gagnon et Khalaf (2016).
Les résultats présentés au tableau 4 nous aident à apprécier l’impact d’un grand nombre de facteurs en termes d’identification d’un modèle. En fait, l’évidence présentée montre que la présence de facteurs à la fois domestiques et globaux, même lorsque le modèle estimé ne compte que deux facteurs, n’est pas identifié. Notre approche permet donc de mettre en valeur ces problèmes dans un contexte d’évaluation d’actifs mais comporte également des implications pour la finance internationale, suivant que plusieurs modèles comportent dans leur forme la plus large la présence de facteurs globaux et domestiques. La littérature n’a pas clairement statué sur le fait que les économies sont complètement intégrées et que seuls des facteurs globaux sont importants pour l’évaluation d’actifs dans un contexte international. Nous avons donc toujours besoin de modèles nous permettant d’estimer le prix du risque des facteurs domestiques ou globaux et de calculer sur cette base le coût du capital. L’évidence présentée ici nous suggère d’être prudents lorsqu’il s’agit de l’interprétation des intervalles de confiance classiques dans un contexte d’évaluation d’actifs à l’international.
Tableau 4
Économie internationale – Intervalles de confiance du prix du risque des facteurs de Fama-French globaux et domestiques
Note : Le tableau 4 présente les estimés de l’équation (14) pour différentes spécifications de la mesure du risque systématique. On y rapporte l’intervalle de confiance obtenu pour chaque estimé du facteur de risque. Sur la première ligne de chaque cellule les intervalles de confiance présentés sont obtenus par l’inversion de la statistique de Hotelling présentée à l’équation (8) et l’intervalle de confiance présenté à la ligne suivante est obtenu par la statistique Wald classique. Les prix du risque significatifs à un seuil de 5 % sont représentés par un astérisque. Voir Beaulieu, Gagnon et Khalaf (2016) pour plus de détails sur les données utilisées.
Conclusion
Cet article nous a permis de mettre en valeur un cadre d’application large de la statistique Hotelling inversée, sachant que cette statistique est robuste aux problèmes d’identification et valide en échantillons finis. Par ailleurs, son utilisation ne requiert aucune maximisation numérique et inclut une vérification imbriquée dans la méthode pour l’identification faible et la qualité de la spécification. Finalement, et pour l’objet de notre propos, cette statistique permet d’obtenir de l’information quant à l’identification des facteurs utilisés pour mesurer le prix du risque. Finalement cette statistique nous permet également de détecter les facteurs inutiles.
De façon plus générale, nos résultats mettent en valeur le fait que les différents facteurs inclus dans nos modèles d’évaluation d’actifs sont importants, mais mènent souvent à des modèles non identifiés dans des modèles linéaires additifs, même lorsque les modèles comptent seulement deux facteurs.
Le cas de l’économie américaine nous a permis de montrer qu’une forme moins stricte du modèle du CAPM serait bien identifiée et permettrait au portefeuille de marché d’être important statistiquement. Il s’agit d’un apport intéressant puisque les facteurs de taille et de valeur perdent leur significativité dans le contexte de ce modèle plus large. Et ce peu importe la sous-période étudiée.
Les modèles d’évaluation appliqués aux obligations catastrophe montrent que des problèmes d’identification surgissent lorsque les marchés financiers sont en crise, comme c’était le cas en 2008 et que depuis lors, le prix du risque d’un facteur d’asymétrie est statistiquement significatif réduisant de façon importante le potentiel de diversification des obligations catastrophe.
Finalement, le cadre des modèles d’évaluation d’actifs dans un contexte international remet en question l’utilisation de modèles à plusieurs facteurs puisque dans ce cadre, les modèles étudiés apparaissent très mal identifiés, ce qui soulève la question de comment tester des hypothèses relatives à l’intégration des marchés financiers qui sont d’ordinaire prises en compte avec des facteurs globaux et domestiques.
Dans l’ensemble, l’évidence empirique présentée dans cet article montre que la statistique de Hotelling inversée, tel que développée et implémentée par Beaulieu, Dufour et Khalaf (2013 et 2017) est un outil pertinent et intéressant quand un chercheur doit décider des facteurs à inclure dans un modèle. La significativité de ceux-ci n’est plus le seul critère. Il faut également s’assurer que le prix du risque de ces facteurs soit bien identifié.
Bien que plusieurs alternatives aient été investiguées par Beaulieu, Dufour et Khalaf (2017), soit : i) les composantes principales; ii) des tests conditionnels; iii) l’empilement des portefeuilles du côté gauche de l’équation, aucune de ces approches ne nous permet d’en arriver à des modèles mieux identifiés ou mieux spécifiés que ceux dont j’ai discuté ici. Ce qui m’apparaît important de souligner est que le portefeuille de marché est un facteur informatif mais que dans l’ensemble de nos résultats ce n’est pas le cas du facteur représentant le ratio de la valeur au livre avec la valeur au marché, non plus que le facteur de momentum. Il demeure que dans le contexte des modèles présentant plusieurs facteurs non identifiés, l’approche présentée ici ne permet pas de discriminer à travers ces facteurs. La question qui se pose si les facteurs ne sont pas bien identifiés mais qu’ils sont cependant pertinents, est comment réorganiser l’information qu’ils contiennent afin d’obtenir, ultimement, des intervalles de confiance pour le prix du risque qui nous permettront de prendre des décisions d’investissement et de financement éclairées.
Appendices
Remerciements
Cet article a bénéficié du support financier du Conseil de recherche en sciences humaines du Canada et de la Chaire RBC en innovations financières. L’auteur remercie Jean-Marie Dufour, Marie-Hélène Gagnon, Lynda Khalaf, Richard Luger et Olena Melin ainsi que les participants à la session plénière intitulée « Le prix du risque » pour leurs commentaires et suggestions. Les erreurs sont la seule responsabilité de l’auteur.
Notes
-
[1]
Le bêta est défini comme la sensibilité du rendement d’un actif à la variation unitaire du rendement d’un facteur qui est dans le modèle du CAPM le portefeuille de marché ou le rendement d’un autre facteur dans un modèle plus large.
-
[2]
En fait, en présence de problèmes d’identification, la probabilité de couverture est de beaucoup inférieure à 95 % et peut même être nulle.
-
[3]
À noter que, tel que nous le montrerons plus bas, ce modèle très flexible d’évaluation d’actifs peut inclure des restrictions non linéaires impliquant le taux zéro-bêta et les primes de risque.
-
[4]
Cette statistique est pour le cas le plus simple où γ0est égal à γc. Pour la généralisation de la statistique lorsque les deux gammas ne sont pas les mêmes, voir Beaulieu, Dufour et Khalaf (2017).
Bibliographie
- Beaulieu, M.-C., J.-M. Dufour et L. Khalaf (2007), « Multivariate Tests of Mean-variance Efficiency with Possibly Non-Gaussian Errors : An Exact Simulation-based Approach », Journal of Business and Economic Statistics, 25 : 398-410.
- Beaulieu, M.-C., J.-M. Dufour et L. Khalaf (2013), « Identification-robust Estimation and Testing of the Zero-beta CAPM », The Review of Economics Studies, 80 : 892-924.
- Beaulieu, M.-C., J.-M. Dufour et L. Khalaf (2017), « Weak Beta, Strong Beta: Multi-factor Pricing and Rank Restriction », Document de travail.
- Beaulieu, M.-C., J.-M. Dufour et L. Khalaf (2016), « Less is More: Testing Financial Integration Using Identification-robust Asset Pricing Models », Journal of International Financial Markets, Institutions & Money, 45 : 171-190.
- Beaulieu, M.-C., L. Khalaf et O. Melin (2017), « Do Catastrophe Bond Mutual Funds Constitute Zero-beta Investments? : Identification-robust Evidence », Document de travail.
- Black, F. (1972), « Capital Market Equilibrium with Restricted Borrowing », The Journal of Business, 45 : 444-455.
- Black, F., M. C. Jensen et M. S. Scholes (1972), « The Capital Asset Pricing Model: Some Empirical Tests », in Jensen, M. C., Studies in the Theory of Capital Markets, p. 79-121.
- Blume, M. E. et I. Friend (1973), « A New Look at the Capital Asset Pricing Model », The Journal of Finance, 28 : 19-34.
- Campbell, R. H., Y. Liu et H. Zhu (2016), « …and the Cross-section of Expected Returns », The Review of Financial Studies, 29 : 5-68.
- Chen, N.-F., R. Roll et S. A. Ross (1986), « Economic Forces and the Stock Market », The Journal of Business, 59 : 383-403.
- Cummins, J. D. et M. A. Weiss 2009), « Convergence of Insurance and Financial Markets: Hybrids and Securitized Risk-transfer Solutions », Journal of Risk and Insurance, 76 : 493-545.
- Dufour, J.-M. (1997), « Some Impossibility Theorems in Econometrics, with Applications to Structural and Dynamic Models », Econometrica, 65 : 1365-1389.
- Dufour, J.-M. et C. Hsiao (2008), « Identification », The New Palgrave Dictionary of Economics, 2e édition.
- Fama, E. F. et K. R. French (1992), « The Cross-section of Expected Stock Returns », Journal of Finance, 47 : 427-465.
- Fama, E. F. et K. R. French (1993), « Common Risk Factors in the Returns on Stocks and Bonds », Journal of Financial Economics, 33 : 3-56.
- Fama, E. F. et J. D. MacBeth (1973), « Risk, Return, and Equilibrium: Empirical Tests », The Journal of Political Economy, 81 : 607-636.
- Gibbons, M. R. (1982), « Multivariate Tests of Financial Models », Journal of Financial Economics, 10 : 3-27.
- Gibbons, M. R., S. A. Rosset et J. Shanken (1989), « A Test of the Efficiency of a Given Portfolio », Econometrica, 57 : 1121-1152.
- Gollier, C. (2016), « Valorisation des investissements ultra-longs et développement durable », L’Actualité économique, 92 : 667-701.
- Gospodinov, N., R. Kanet et C. Robotti (2013), « Misspecification-robust Inference in Linear Asset Pricing Models with Irrelevant Risk Factors », Federal Reserve Bank of St-Louis, Working paper no 1698076877.
- Jensen, M. C. (1968), « The Performance of Mutual Funds in the Period 1945-1964 », The Journal of Finance, 23 : 389-416.
- Kan, R., C. Robotti et J. Shanken (2013), « Pricing Model Performance and the Two-pass Cross-sectional Regression Methodology », The Journal of Finance, 68 : 2617-2649.
- Khalaf, L. et H. Schaller (2016), « Identification and Inference in Two-pass Asset Pricing Models », Journal of Economic Dynamic and Control, 70 : 165-177.
- Kleibergen, F. et Z. Zhan (2015), « Unexplained Factors and their Effects on Second Pass R-squared’s », Journal of Econometrics, 1 : 101-116.
- Kraus, A. et R. H. Litzenberger (1976), « Skewness Preference and the Valuation of Risk Assets », The Journal of Finance, 31 : 1085-1100.
- Lewellen, J., Nagel, S. et J. Shanken (2010), « A Skeptical Appraisal of Asset-pricing Tests », Journal of Financial Economics, 92 : 175-194.
- Lintner, J. (1965), « The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets », The Review of Economics and Statistics, 47 : 13-37.
- MacKinlay, A. C. (1985), « On Multivariate Tests of the CAPM », Journal of Financial Economics, 18 : 341-371.
- Merton, R. (1973), « An intertemporal Capital Asset Pricing Model », Econometrica, 41 : 867-887.
- Mossin, J. (1966), « Equilibrium in a Capital Asset Market », Econometrica, 34 : 768-783.
- Pastor, L. et R. F. Stambaugh (2003), « Liquidity Risk and Expected Stock Returns », The Journal of Political Economy, 111 : 642-685.
- Shanken, J. et G. Zhou (2007), « Estimating and Testing Beta Pricing Models: Alternative Methods and their Performance in Simulations », Journal of Financial Economics, 84 : 40-86.
- Sharpe, W. F. (1964), « Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk », The Journal of Finance, 19 : 425-442.
- Ross, S. A. (1976), « The Arbitrage Theory of Capital Asset Pricing », Journal of Economic Theory, 13 : 341-360.
- Treynor, J. L. (1961), « Market Value, Time, and Risk », Document de travail.
- Treynor, J. L. (1962), « Toward a Theory of Market Value of Risky Assets », Document de travail.
List of tables
Tableau 1
Économie américaine
Intervalles de confiance du prix du risque des trois facteurs de Fama-French
Note : Ce tableau présente  la moyenne de chaque facteur du modèle d’évaluation d’actifs pour l’ensemble de l’économie américaine ainsi que l’ensemble de confiance obtenu par l’inversion de la statistique de Hotelling. Les données incluent 12 portefeuilles industrie pour le vecteur de variables endogènes ainsi que les facteurs de i) marché, ii) taille, iii) valeur au livre sur valeur de marché, toutes tirées du site de Kenneth French allant de 1961 à 2010. Voir Beaulieu, Dufour et Khalaf (2017) pour l’ensemble des détails concernant les données. Les prix du risque significatifs à un seuil de 5 % sont représentés par un astérisque.
la moyenne de chaque facteur du modèle d’évaluation d’actifs pour l’ensemble de l’économie américaine ainsi que l’ensemble de confiance obtenu par l’inversion de la statistique de Hotelling. Les données incluent 12 portefeuilles industrie pour le vecteur de variables endogènes ainsi que les facteurs de i) marché, ii) taille, iii) valeur au livre sur valeur de marché, toutes tirées du site de Kenneth French allant de 1961 à 2010. Voir Beaulieu, Dufour et Khalaf (2017) pour l’ensemble des détails concernant les données. Les prix du risque significatifs à un seuil de 5 % sont représentés par un astérisque.
Tableau 2
Économie américaine
Intervalles de confiance du prix du risque des trois facteurs de Fama-French
Note : Ce tableau présente  la moyenne de chaque facteur du modèle d’évaluation d’actifs pour l’ensemble de l’économie américaine ainsi que l’intervalle de confiance obtenu par l’inversion de la statistique de Hotelling dans le cas où les rendements du portefeuille de marché et des rendements endogènes ne sont pas pour la même mesure excédentaire. Les données incluent 12 portefeuilles industrie pour le vecteur de variables endogènes ainsi que les facteurs de i) marché, ii) taille, iii) valeur au livre sur valeur de marché, toutes tirées du site de Kenneth French allant de 1961 à 2010. Voir Beaulieu, Dufour et Khalaf (2017) pour l’ensemble des détails concernant les données. Les prix du risque significatifs à un seuil de 5 % sont représentés par un astérisque.
la moyenne de chaque facteur du modèle d’évaluation d’actifs pour l’ensemble de l’économie américaine ainsi que l’intervalle de confiance obtenu par l’inversion de la statistique de Hotelling dans le cas où les rendements du portefeuille de marché et des rendements endogènes ne sont pas pour la même mesure excédentaire. Les données incluent 12 portefeuilles industrie pour le vecteur de variables endogènes ainsi que les facteurs de i) marché, ii) taille, iii) valeur au livre sur valeur de marché, toutes tirées du site de Kenneth French allant de 1961 à 2010. Voir Beaulieu, Dufour et Khalaf (2017) pour l’ensemble des détails concernant les données. Les prix du risque significatifs à un seuil de 5 % sont représentés par un astérisque.
Tableau 3
Obligations catastrophe
Intervalles de confiance du prix du risque des facteurs du CAPM asymétrique
Note : Ce tableau présente  la moyenne de chaque facteur du modèle d’évaluation d’actifs pour l’ensemble des obligations catastrophe ainsi que l’ensemble de confiance obtenu par l’inversion de la statistique de Hotelling pour chacun des facteurs nommément le rendement du portefeuille de marché et le rendement du portefeuille de marché au carré. On rapporte l’intervalle de confiance obtenu pour le prix du facteur de risque. Les facteurs de risque sont le rendement du portefeuille de marché et le rendement du portefeuille de marché au carré suivant le modèle du CAPM asymétrique (Kraus et Litzenberger, 1976) Sur la première ligne de chaque cellule les intervalles de confiance présentés sont obtenus par l’inversion de la statistique de Hotelling présentée à l’équation (8) et l’intervalle de confiance présenté à la ligne suivante est obtenu par la statistique Wald classique. La variable endogène est le rendement des fonds mutuels catastrophes tirés de Bloomberg. Voir Beaulieu, Khalaf et Melin (2017) pour plus de détails. Les prix du risque significatifs à un seuil de 5 % sont représentés par un astérisque.
la moyenne de chaque facteur du modèle d’évaluation d’actifs pour l’ensemble des obligations catastrophe ainsi que l’ensemble de confiance obtenu par l’inversion de la statistique de Hotelling pour chacun des facteurs nommément le rendement du portefeuille de marché et le rendement du portefeuille de marché au carré. On rapporte l’intervalle de confiance obtenu pour le prix du facteur de risque. Les facteurs de risque sont le rendement du portefeuille de marché et le rendement du portefeuille de marché au carré suivant le modèle du CAPM asymétrique (Kraus et Litzenberger, 1976) Sur la première ligne de chaque cellule les intervalles de confiance présentés sont obtenus par l’inversion de la statistique de Hotelling présentée à l’équation (8) et l’intervalle de confiance présenté à la ligne suivante est obtenu par la statistique Wald classique. La variable endogène est le rendement des fonds mutuels catastrophes tirés de Bloomberg. Voir Beaulieu, Khalaf et Melin (2017) pour plus de détails. Les prix du risque significatifs à un seuil de 5 % sont représentés par un astérisque.
Tableau 4
Économie internationale – Intervalles de confiance du prix du risque des facteurs de Fama-French globaux et domestiques
Note : Le tableau 4 présente les estimés de l’équation (14) pour différentes spécifications de la mesure du risque systématique. On y rapporte l’intervalle de confiance obtenu pour chaque estimé du facteur de risque. Sur la première ligne de chaque cellule les intervalles de confiance présentés sont obtenus par l’inversion de la statistique de Hotelling présentée à l’équation (8) et l’intervalle de confiance présenté à la ligne suivante est obtenu par la statistique Wald classique. Les prix du risque significatifs à un seuil de 5 % sont représentés par un astérisque. Voir Beaulieu, Gagnon et Khalaf (2016) pour plus de détails sur les données utilisées.





 10.7202/1040502ar
10.7202/1040502ar