Abstracts
Résumé
L’augmentation constante de l’espérance de vie engendre l’heureux risque de vivre au-delà de nos actifs. Ce risque n’est non seulement pas diversifiable pour les individus, mais il ne l’est que difficilement pour les fonds de pension et les assureurs. Nous illustrons comment différents modèles à facteurs peuvent être utilisés afin de valoriser les titres financiers qui permettraient aux fonds de pension de transférer ce risque à d’autres parties. Nous montrons que le risque de longévité, bien que mesurable au moyen d’un modèle en composantes principales, est mieux mesuré au moyen de modèles plus structurels. Néanmoins, le risque de modèle associé à ces modèles structurels demeure tel qu’il est fort possible que la prime que demanderait un assureur pour assumer le risque de longévité soit supérieure à la volonté à payer des promoteurs de fonds de pension. Cet écart pourrait expliquer la quasi-absence de marché pour la gestion du risque de longévité.
Article body
Introduction
L’intérêt pour la modélisation de l’espérance de vie d’une population n’est pas une affaire récente[1]. Ce qui est plus récent toutefois est l’intérêt de modéliser l’espérance de vie à un âge relativement avancé, en particulier à l’âge normal de la retraite (voir Robine et Michel, 2004; Rechel et al., 2013). Plusieurs se sont penchés sur les multiples facettes de la démographie de l’après-guerre (voir Cairns et al., 2011, pour plus de détails), et beaucoup s’accordent pour dire que le vieillissement de la population est un problème imminent et potentiellement catastrophique si aucun changement n’est apporté au filet social des pays de l’OCDE. En l’absence d’une gestion appropriée des risques associés à ce phénomène, l’augmentation de la longévité nécessitera que les travailleurs actuels accumulent davantage de capital financier pour subvenir à leurs besoins au moment où ils quitteront le marché du travail.
Le « risque de longévité » peut donc être défini comme étant le risque financier découlant de la possibilité que l’espérance de vie anticipée pour les rentiers soit inférieure à leur espérance de vie réelle. Or, ce risque de longévité est, pour l’industrie des assurances et des régimes de pension, un risque difficilement diversifiable; il est systématique de par sa nature puisqu’il touche l’ensemble de la population. Plusieurs outils financiers ont été proposés pour faciliter la redistribution de ce risque sur les marchés de capitaux. Toutefois, le nombre de transactions, la liquidité et la profondeur de ces marchés n’ont aucune commune mesure avec l’importance des pertes financières potentielles liées au risque de longévité[2]. Conséquemment, l’objectif de ce document est de mieux comprendre comment l’état actuel des connaissances sur la dynamique de survie des populations avancées en âge affecte le développement de ces outils financiers.
Le risque de longévité revêt une grande importance pour la rentabilité et la pérennité du marché des rentes viagères. Or, les tables actuarielles ont historiquement sous-estimé l’espérance de vie conditionnelle à avoir atteint l’âge de 65 ans. Ces erreurs d’estimation passées forment un plaidoyer sérieux pour une mortalité stochastique (c’est-à-dire que l’espérance de vie augmente d’une manière imprévisible), tel qu’argumenté par Olivieri (2001), Dahl (2004), Biffis (2005), Cairns et al. (2006a, 2006b), et Planchet et al. (2006). Il s’ensuit que les vendeurs d’annuité qui utilisent des modèles où la mortalité suit un processus déterministe sous-estiment grossièrement leurs provisions, surestimant ainsi leur ratio de solvabilité.
Bien qu’on ne s’entende pas encore sur l’outil exact qui permettrait la gestion la plus efficace du risque de longévité, plusieurs produits dérivés ont été proposés. Afin de mieux comprendre leur insuccès sur les marchés, nous ferons l’examen d’un contrat à terme (forward) de longévité sur la population canadienne. Grâce à la modélisation et à la valorisation du plus simple des outils de gestion du risque de longévité qui aient été proposés, nos résultats mettent en exergue certaines causes vraisemblables de l’absence de transactions sur ces marchés[3]. Nous démontrons de plus que l’incertitude associée au « meilleur » modèle pour décrire le processus statistique de la longévité est telle que la prime forward est probablement trop élevée par rapport à la volonté à payer du promoteur du fonds. Si on ajoute à ce risque de modèle le risque de base auquel s’expose un fonds de pension pour lequel la distribution démographique de ses participants a très peu de chance d’être la même que pour l’indice sous-jacent au contrat forward de longévité, il est peut-être compréhensible que le marché du transfert de risque de longévité au moyen d’outils financiers soit pratiquement inexistant.
Le reste du document est divisé comme suit. La première section présente une courte revue de la littérature pertinente en démographie qui s’est penchée sur la question de la modélisation des taux de mortalité dans les pays développé en général, et au Canada en particulier. La section 2 est dédiée à la présentation du problème économique important que représente le risque de longévité et sa gestion. Nous présentons ensuite, dans la section 3, un outil de gestion du risque de longévité, nommément un contrat à terme (forward) sur la longévité qui aurait été vendu par un investisseur (ou un assureur) désireux de s’exposer à ce risque, et nous y présentons les résultats de notre recherche. Finalement, nous discutons de nos résultats et concluons avec la dernière section.
1. Un retour sur les contributions récentes
1.1 Les modèle démographiques de mortalité
La modélisation des taux de mortalité, et leur importance pour la santé financière des régimes de retraite publics et privés, a donné naissance à une nouvelle littérature en économie financière, en assurance et en démographie. La majorité des études en démographie s’entendent pour dire que la croissance démographique de la population des aînés (65 ans et plus) dépassera largement la croissance de la population en général. Ainsi, alors que la population âgée de 65 ans et plus représente aujourd’hui environ 13,5 % de la population canadienne, elle atteindra vraisemblablement un plateau à près de 24 % en 2035. La proportion des « aînessimes », soit ceux âgés de 80 ans et plus, connaîtra une augmentation encore plus importante pendant cette période. Ne représentant que 3 % de la population aujourd’hui, on s’attend à ce que les aînessimes représentent 8 % de la population en 2035. Pour mettre cette proportion en contexte, notons que la population âgée de 65 ans et plus représentait environ 8 % de la population canadienne au milieu des années soixante-dix. Ainsi, le poids démographique (et politique a fortiori) des aînessimes dans vingt ans sera approximativement celui des aînés d’il y a quarante ans. Il apparait donc essentiel d’être capable d’anticiper correctement le taux de mortalité de la population actuelle dans le futur.
Pour ce faire, Booth et Tickle (2008) définissent trois grandes classes de modèles de mortalité : les modèles anticipatifs, les modèles explicatifs, et les modèles stochastiques. Dans le cadre des modèles anticipatifs, les experts démographiques donnent leurs prévisions sur l’évolution de la mortalité. Celles-ci contiennent généralement une cible d’espérance vie, ainsi qu’un scénario pessimiste et optimiste. Par exemple, The US Social Security Trustees fournit ses anticipations d’amélioration de l’espérance de vie pour chaque âge. Cette méthode a l’avantage d’incorporer plusieurs sources de données, qu’elles soient qualitatives ou quantitatives. Cependant, elle est aussi très subjective ce qui fait en sorte que le biais conservateur des experts les amène souvent à sous-estimer l’amélioration de l’espérance de vie.
Les modèles explicatifs, quant à eux, cherchent à déterminer quelles sont les causes de mortalité, comment celles-ci vont évoluer, et quel en sera l’impact sur l’espérance de vie (voir Manton et al., 1991 et 1992; Wilmoth, 1995; Hanewald, 2009; Gaille, 2012). Cette approche demande que nous comprenions quel est l’impact des avancés médicales et médécinales sur l’espérance de vie de la population, et que nous comprenions également l’interdépendance et les interractions entre les différentes causes de décès. Le problème avec cette approche est qu’il est difficile de mesurer exactement quelle est la contribution réelle des causes de mortalité et ce, particulièrement auprès des aînés qui sont souvent touchés par plus d’une maladie à la fois. L’ambiguïté qu’on observe ainsi quant aux causes réelles d’un décès augmente la difficulté de mesurer correctement la contribution à la longévité humaine de telle ou telle avancée médicale. Qui plus est, les prévisions que nous pouvons faire basées sur les causes de décès ne semblent bonnes qu’à très court terme, ce qui en réduit la portée dans un contexte où nous cherchons à prévoir la croissance du passif actuariel des fonds de pension[4]. En pratique ces modèles ne sont donc pas utilisés tant pour prédire la mortalité que pour expliquer son évolution passée.
1.2 Les modèles stochastiques de mortalité
Les modèles stochastiques de mortalité forment une famille de modèles d’un intérêt particulier dans un cadre de gestion du risque. Ils reposent sur l’hypothèse d’une continuité entre l’évolution passée de la mortalité et son évolution future. Dans le cadre de ces modèles, on suppose que l’évolution des taux de mortalité, comme ceux présentés dans le graphique 1, suit un processus stochastique. Grâce à cette hypothèse, il est possible de produire une distribution de prévisions, et non plus uniquement une valeur déterministe. Il est par conséquent possible d’obtenir une certaine mesure du risque de longévité en regardant la distribution de la longévité future au moyen de simulations de Monte-Carlo. Ces mesures de distribution demeurent évidemment spécifiques au modèle stochastique sous-jacent. Cairns et al. (2008) livre une intéressante revue de la littérature sur ces modèles.
Graphique 1
Probabilité de décès à travers le temps
Femmes
Hommes
Évolution au Canada de la probabilité de décès, au cours des années 1921 à 2009, pour les femmes et les hommes de différents âges. Autant chez les hommes que chez les femmes, le taux de mortalité a décru significativement au cours du dernier siècle. En plus de cette tendence à la baisse, ce graphique illustre aussi une autre régularité empirique : l’amélioration de la longévité est plus marqué aux âges avancés (ici 85 ans) qu’elle ne l’est à des âges moins avancés (ici 65 ans).
Nous pouvons tracer les débuts modernes des tentatives de paramétrisation des séries temporelles de mortalité aux travaux de Heligman et Pollard (1980). Leur approche se résumait à diviser la vie d’une cohorte d’individus en des groupes distincts qui dépendent de leur âge (disons un groupe de jeunes, de matures et de vieux). Les dynamiques de mortalité particulières à ces trois groupes d’âge sont par la suite modélisées en utilisant huit variables (qui prennent le nom de A, B, C, D, E, F, G, H) qui représentent l’ensemble des causes de décès aux différents âges, soit la mortalité infantile, les risques de décès accidentels lors des années matures, et les décès attribuables à la maladie lors du vieil âge. Un problème potentiel du modèle de mortalité proposé par Heligman et Pollard (1980) est de surexpliquer les données en échantillon, ce qui risque alors de générer de mauvaises prédictions hors-échantillon. Lorsqu’on ne s’intéresse qu’au cas des personnes âgées, comme ce devrait être le cas lorsque nous parlons du risque de longévité pour un fonds de pension, le modèle de Heligman et Pollard (1980) se résume à modéliser le taux de survie comme ![]() , avec x > 50 (voir Thatcher, 1990) et qx la probabilité de décès. Dans Sharrow et al. (2013), les paramètres G et H sont respectivement l’ordonnée à l’origine d’une loi de Gompertz à la naissance (voir Gompertz, 1825) et de la pente de cette même distribution (pour plus de détails, voir Thatcher, 1987). La complexité du modèle à 8 facteurs de Heligman et Pollard (1980) contraste grandement avec le modèle parcimonieux de Lee et Carter (1992) qui suit, et qui est vraisemblablement le modèle de mortalité le plus connu.
, avec x > 50 (voir Thatcher, 1990) et qx la probabilité de décès. Dans Sharrow et al. (2013), les paramètres G et H sont respectivement l’ordonnée à l’origine d’une loi de Gompertz à la naissance (voir Gompertz, 1825) et de la pente de cette même distribution (pour plus de détails, voir Thatcher, 1987). La complexité du modèle à 8 facteurs de Heligman et Pollard (1980) contraste grandement avec le modèle parcimonieux de Lee et Carter (1992) qui suit, et qui est vraisemblablement le modèle de mortalité le plus connu.
1.2.1 Modèle Lee-Carter
Le modèle de Lee et Carter (1992) s’intéresse à la variable ![]() qui représente le taux de mortalité entre les âges x et x +1 mesuré à l’an t. Le modèle de Lee-Carter, s’écrit ainsi comme suit
qui représente le taux de mortalité entre les âges x et x +1 mesuré à l’an t. Le modèle de Lee-Carter, s’écrit ainsi comme suit
où les εx(t) sont indépendants de moyenne 0 et de variance σ2ε. Ce système d’équations stipule ainsi que le taux de mortalité mesuré pour chaque âge x est une réalisation bruitée d’un processus qui ne dépend que d’un facteur commun, soit k(t), et de paramètres de niveau (ax) et de sensibilité au facteur commun (bx) spécifique à chaque âge. Pour identifier le facteur commun, Lee et Carter (1992) présume qu’il s’agit du facteur qui explique un maximum de variation dans les séries de log-mortalité; on peut donc démontrer que k(t) correspond à la première composante principale des séries ![]() [5]. Le modèle Lee-Carter n’est par conséquent qu’une application d’un modèle à composantes principales.
[5]. Le modèle Lee-Carter n’est par conséquent qu’une application d’un modèle à composantes principales.
Le plus grand avantage du modèle Lee-Carter est qu’il est particulièrement simple, qu’il explique « bien » (c’est-à-dire rétroactivement et en échantillon) une grande partie de la variance des taux de mortalité et que ses paramètres ont une interprétation bien définie[6]. Bien que le modèle Lee-Carter s’intéresse à la modélisation de la mortalité, l’objet d’intérêt est plutôt, de manière générale, la probabilité de décès. Dénotons qx(t) la probabilité qu’un individu âgé de x à l’an t décède avant d’atteindre l’âge x +1. Au temps t +1, on pourra mesurer la réalisation ![]() à l’aide du taux de mortalité correspondant. Afin d’évaluer la valeur espérée de flux monétaires futurs à l’aide du modèle Lee-Carter, nous devons d’abord prévoir le taux de mortalité dans le futur,
à l’aide du taux de mortalité correspondant. Afin d’évaluer la valeur espérée de flux monétaires futurs à l’aide du modèle Lee-Carter, nous devons d’abord prévoir le taux de mortalité dans le futur, ![]() , puis transformer ces taux en probabilité de décès
, puis transformer ces taux en probabilité de décès ![]() . Puisque les paramètres spécifiques à l’âge (ax,bx) sont des constantes, il suffit donc de prévoir l’évolution du facteur commun k. Pour ce faire, dans le cadre du modèle Lee-Carter, il est d’usage de supposer que k suit une marche aléatoire avec dérive,
. Puisque les paramètres spécifiques à l’âge (ax,bx) sont des constantes, il suffit donc de prévoir l’évolution du facteur commun k. Pour ce faire, dans le cadre du modèle Lee-Carter, il est d’usage de supposer que k suit une marche aléatoire avec dérive,
où μ et σ sont des paramètres à estimer et u(t +1) est présumée être une variable aléatoire tirée d’une loi normale centrée reduite[7]. En se basant sur les données canadiennes de mortalité entre 1921 et 2009, nous trouvons que le modèle Lee-Carter explique près de 98 % de la mortalité chez les femmes et près de 94 % chez les hommes[8], Un autre avantage du modèle Lee-Carter est qu’il permet de faire des prévisions à long-terme hors-échantillon tout en offrant des intervalles de confiance qui sont associés à la nature stochastique des améliorations dans la mortalité d’une population ou d’une partie de la population.
Le modèle Lee-Carter n’a pas que des avantages. En particulier, il est rébarbatif au lissage de données entre les âges, et la structure linéaire de ses paramètres est présumée invariable dans le temps. D’autre part, les erreurs sont présumées être distribuées de manière homoscédastique. Or, cette hypothèse d’homoscédasticité implique que les termes d’erreurs sont indépendants de l’âge de la cohorte, ce qui ne correspond pas vraiment à la réalité selon Planchet et Lelieur (2007). En effet, les termes d’erreurs sont beaucoup plus importants aux âges avancés, ce qui cause des problèmes de validation économique quand le but est de mesurer, par exemple, la valeur présente des promesses faites aux futurs retraités (c’est-à-dire le passif actuariel). Le modèle Lee-Carter de base consière qu’il n’y a aucune différence dans la sensibilité des différents âges à l’évolution de la mortalité agrégée. Nous pourrions même dire que le modèle Lee-Carter ne prend nullement en considération la possibilité qu’il puisse y avoir un effet de cohorte dans les données de la mortalité. Cette absence d’un effet de cohorte est ainsi associée à un autre problème du modèle Lee-Carter puisqu’on y suppose une évolution de la mortalité qui est la même pour toutes les cohortes. Toutefois, Bongaarts (2004) trouve que la mortalité décroît plus lentement pour les jeunes cohortes et plus rapidement pour les cohortes plus vieilles. De manière à corriger les différents problèmes associés au modèle Lee-Carter de base, Renshaw et Haberman (2006) ont proposé d’ajouter tout simplement un paramètre qui prendrait en compte l’effet de la cohorte, soit l’année de naissance d’un groupe d’individus.
1.2.2 Modèle CBD
Le modèle de Renshaw et Haberman (2006) n’est pas tant un nouveau modèle qu’un ajout de paramètres au modèle Lee-Carter. Un modèle de mortalité qui sort du paradigme Lee-Carter est celui de Cairns, Blake et Dowd (2006b), ou modèle CBD ci-après. Le modèle CBD considère les réalisations des probabilités de décès selon la structure suivante :
où les εx(t) sont indépendants de moyenne 0 et de variance σ2t. Ainsi, un premier facteur capture la tendance générale dans l’évolution (du logit) des probabilités de décès, alors qu’un second facteur permet de laisser évoluer les probabilités de décès à travers le temps en fonction de variables spécifiques de chaque tranche d’âge. Pour estimer les Ki(t) étant donnée les probabilités de décès estimées pour l’année t, il suffit ainsi de régresser linéairement leur logit sur une l’âge centré, x − x̅ ; la constante et la pente fournissent des estimateurs des facteurs au temps .
Pour prévoir les probabilités de décès futures, il faut ensuite prévoir l’évolution de K1 et K2. Le modèle prédictif suggéré par CBD est une marche aléatoire avec dérive bidimensionnelle
où C est la Choleski de la matrice de covariance du système et où les u(t) sont des erreurs indépendantes de distribution normale centrée réduite [9]. L’hypothèse de marche aléatoire peut aussi être relaxée,
un modèle que nous dénoterons CBD-VAR, où B est une matrice 2 × 2 de paramètres. Le modèle en n’est qu’un cas particulier du modèle en, où ![]() . L’utilisation du modèle VAR pour les facteurs CBD est un cas particulier du VARIMA étudié par Chan, Li et Li (2014). Nous suivons la pratique standard et estimons les systèmes par maximum de vraisemblance.
. L’utilisation du modèle VAR pour les facteurs CBD est un cas particulier du VARIMA étudié par Chan, Li et Li (2014). Nous suivons la pratique standard et estimons les systèmes par maximum de vraisemblance.
L’avantage du modèle CBD sur l’ensemble de ses concurrents est qu’il nous permet d’obtenir des facteurs qui, par construction, ne varient pas quand nous ajoutons des observations. Ceci contraste avec les modèles de type Lee-Carter (ou à composantes principales) dont la valeur des facteurs change à chaque fois que nous ajoutons une année de données. Plus précisément, pour le modèle de Lee-Carter, à l’ajout d’une nouvelle donnée au temps t, les valeurs estimées de ![]() , changent.
, changent.
Un autre avantage du modèle CBD est qu’il utilise des mesures des probabilités de survie (q) plutôt que des mesures du taux de mortalité (m) comme dans les modèles de la famille Lee-Carter. Or les actuaires semblent largement plus à l’aise de travailler sur la série « q » que sur la série « m », qui n’est qu’une approximation du taux instantané de survie. Le plus grand problème du modèle CBD est qu’il nous donne une série associée non pas à q, ce qui aurait été plus intuitif, mais au logit (q)[10]. Bien qu’il soit un peu moins intuitif d’utiliser la fonction logit(), elle est très proche de la distribution de Gompertz qui a été utilisée par Heligman et Pollard (1980) pour modéliser l’espérance de vie à un âge avancé.
Le modèle CBD est par conséquent particulièrement utile lorsqu’on s’intéresse aux prédictions de mortalité des populations qui ont atteint l’âge normal de la retraite. Pour ces population, le modèle performe assez bien lorsqu’on s’intéresse aux projections des taux de survie pour les 10 prochaines années (voir Cairns et al., 2011). La performance du modèle tombe rapidement toutefois lorsqu’on tente de projeter encore plus loin les probabilités de décès à cause essentiellement d’un risque de modèle.
2. Le cadre économique
2.1 Le marché incomplet de la longévité et les modèles factoriels
Comme nous l’avons déjà mentionné, le modèle de Lee-Carter extrait essentiellement la première composante principale, dans le domaine du logarithme, des séries de mortalités réalisées. Le modèle CBD travaille plutôt avec le logit des séries de probabilités de décès. Le graphique 2 présente l’évolution dans le temps du facteur k de Lee-Carter et des facteurs K1 et K2 de CBD pour la population canadienne. Que nous mettions l’accent sur k ou K1, nous remarquons un déclin marqué des probabilités de décès, ce qui met en évidence l’amélioration significative de l’espérance de vie au cours du dernier siècle. Malgré les différences méthodologiques entre les deux modèles, la corrélation entre le facteur k de Lee-Carter et le facteur K1 de CBD, rapportée dans le tableau 1, est de 99,86 % pour les femmes et de 99,36 % pour les hommes
Graphique 2
Facteurs des modèles Lee-Carter et Cairns, Blake et Dowd (CBD)
Facteur Lee-Carter
Premier Facteur CBD
Deuxième Facteur CBD
Évolution au Canada, au cours des années 1921 à 2009, du facteur sous-jacent au modèle de Lee-Carter et des facteurs du modèle CBD, K1 (·) et K2 (·) au Canada, pour les hommes (![]() ) et pour les femmes (
) et pour les femmes (![]() ) de 55 à 105 ans.
) de 55 à 105 ans.
Tableau 1
Corrélations entre les différents facteurs
La partie triangulaire inféreure présente la corrélation entre les facteurs des modèles de Lee-Carter (LC) et CBD (K1 et K2) et les trois composantes principales du logit de la mortalité pour les femmes canadiennes entre 1921 et 2009. La partie triangulaire supérieure présente les corrélations correspondantes pour les hommes.
Suivant la logique du modèle Lee-Carter où le facteur n’est ni plus ni moins que la première composante principale de log-mortalité, nous pouvons extraire les composantes principales du logit des probabilités de décès. Ceci équivaut essentiellement à appliquer la technique de base du modèle Lee-Carter sur une différente transformation des séries de mortalité. Ainsi, à l’extraction des trois premières composantes principales qui expliquent linéairement un maximum de variation dans les données considérées par CBD, on obtient :

où l’on rapporte le pourcentage de la variance expliquée par chacune de composante ainsi que la somme pour les trois composantes. Le graphique 3 présente les propriétés longitudinales de ces trois composantes principales dans le temps[11].
Le tableau 1 rapporte une corrélation avoisinant 100 % entre le facteur k de Lee-Carter et CPi, autant pour les femmes que pour les hommes. Nous pouvons donc en conclure que le choix des séries, la log-mortalité ou le logit des probabilités de décès, n’a que peu d’impact sur l’analyse de la tendance centrale de la longévité à travers le temps. D’autre part, le tableau 1 rapporte aussi une corrélation de 99,89 % chez les femmes (et de 99,54 % chez les hommes) entre CPi et K1, le premier facteur du modèle CBD. Il est donc évident que la tendance capturée par K1 est le facteur ayant le pouvoir explicatif le plus important pour modéliser l’évolution (du logit) des probabilités de décès.
Graphique 3
Composantes principales des probabilités de décès
Première Composante Pricipale
Deuxième Composante Pricipale
Troisième Composante Pricipale
Évolution au Canada, au cours des années 1921 à 2009, des trois composantes principales du logit de la mortalité— ![]() —pour ; pour les hommes (
—pour ; pour les hommes (![]() ) et pour les femmes (
) et pour les femmes (![]() ) de 55 à 105 ans.
) de 55 à 105 ans.
D’autre part, le second facteur CBD, K2, met en évidence le fait que l’espérance de vie des jeunes retraités, ceux qui toucheront des rentes pour une plus grande période, s’améliore plus rapidement que celle des retraités les plus âgés. Cette interprétation du second facteur CBD découle directement de la structure imposée aux facteurs de ce modèle. Plusieurs études ont démontré la supériorité, en échantillon, du modèle CBD sur le modèle de Lee-Carter[12] et il est admis que la structure choisie, réflétant explicitement l’effet de l’âge sur la mortalité, contribue à cette supériorité. Toutefois, les facteurs CBD ont une forte corrélation entre eux : -93,81 % chez les femmes et -84,55 % chez les hommes. Cette corrélation élevée soulèvera des questions importantes lorsqu’il sera question d’évaluer des produits dérivés en marché incomplet.
Il est important de rappeler et d’insister sur le fait que la longévité n’étant pas explicitement transigée, tout produit dérivé tirant sa valeur de l’évolution de la longévité des individus sera transigé en marché dit « incomplet ». En marché incomplet, il est impossible de construire un portefeuille répliquant les flux monétaires du produit dérivé à l’aide du produit sous-jacent. Lorsqu’il est possible de construire un tel portefeuille de réplication, le prix du produit dérivé peut être obtenu en évaluant le prix dudit portefeuille, en supposant l’absence d’opportunité d’arbitrage. En marché incomplet, chaque source de risque qui a un impact sur les flux monétaires du produit dérivé aura un impact sur son prix. La magnitude de cet impact dépendera du prix du risque associé à chaque source de risque. Dans ce contexte, la forte corrélation entre K1 et K2 indique que ces facteurs sont touchés par au moins une source de risque commune, ce qui pourrait compliquer l’identification des prix associés aux différentes sources de risque.
Dans ce contexte, un avantage de l’approche en composantes principales est que ces composantes sont orthogonales par construction. Il serait donc possible de les considérer comme des sources de risque indépendantes les unes des autres. Il est donc intéressant de constater que le second facteur CBD est significativement corrélé avec la seconde composante principale : 30,27 % chez les femmes et 44,97 % chez les hommes. Étant donné le très fort lien entre la première composante principale (CPi), le facteur k de Lee-Carter et le facteur K1 de CBD, la supériorité documentée du modèle CBD vis-à-vis du modèle de Lee-Carter doit provenir de cette corrélation entre K2 et la deuxième composante principale (CP2). Cette observation est d’autant plus intéressante que la seconde composante n’explique que 1,40 % de la variance des probabilités de décès chez les femmes (4,69 % chez les hommes) contre 97,30 % (91,24 %) pour la première composante. Ainsi, en dépit du grand pouvoir explicatif de CPi, le pouvoir explicatif de la seconde composante, et même de la troisième chez les hommes, est non négligeable.
2.2 Quels sont les montants en jeu?
En utilisant les modèles présentés, nous sommes capables de modéliser le risque de mortalité de la population canadienne[13] à l’âge de la retraite à partir des tables de survie disponibles publiquement. Ceci nous permet de calculer dans le tableau 2, pour l’année 2009, quelle prime actuarielle un fonds de pension devrait prévoir afin de distribuer à ses membres retraités une rente pleinement indexée au coût de la vie de 100 $ par année à partir de 65 ans et ce, pour le reste de leur vie en fonction de différents taux d’actualisation des rentes futures[14].
Nous voyons donc qu’un homme âgé de 65 ans qui voudrait une rente annuelle de 100 $ doit avoir accumulé dans son fonds de pension 941 $ si on utilise le modèle CBD et un taux d’actualisation de 6,75 %. Dans le cas d’une femme du même âge, le modèle Lee-Carter demande qu’elle ait accumulé 1 248 $ au taux d’actualisation de 4,89 %. Il est intéressant de noter que le modèle CBD, qui est souvent perçu comme étant le meilleur modèle de prévision de la mortalité aux âges avancés, est celui avec lequel est associé le plus faible paiement de prime pour une annuité immédiate de 100 $. Pour un même taux d’actualisation, la différence entre la prime la plus faible et la prime la plus élevée est de plus de 5 % pour les hommes, et d’environ 1,5 % pour les femmes.
Tableau 2
Primes pour une annuité de 100$
Primes correspondant à une annuité de 100 $ pour un nouveau retraité de 65 ans, basées sur les différents modèles estimés à l’aide des données canadiennes de mortalité de 1921 à 2009. Un taux de 6,75 % est utilisé par plusieurs fonds de pension. Le rapport d’Amours suggère plutôt d’utiliser un taux provenant d’indices d’obligations de très grandes qualités. Les taux de 5,98 % et 4,89 % correspondent aux rendements de tels indices sur obligations corporatives et gouvernementales, respectivement, depuis novembre 2006. Plus précisément, les indices utilisés sont les suivants : (i) FTSE TMX Canada All Corporate Bond Index, (ii) FTSE TMX Canada All Government Bond Index.
Ces différences sont significatives et peuvent peser sur la viabilité à long terme d’un fonds de pension. De plus, comme il n’est question ici que de moyennes, nous sous-estimons grandement l’incertitude autour de l’évolution des facteurs ou autour des paramètres d’un modèle. Cette incertitude quant à la valeur de l’évolution des facteurs et des paramètres s’ajoutera au risque de modèle. Pour un fonds de pension, une sous-estimation systématique de la longévité telle qu’observée dans l’histoire récente, combinée aux risques de modèle, de paramètres ou d’avancées médicales majeures, pourrait se traduire en un sous-financement colossal des fonds de pension.
2.3 Prédictions hors échantillon des probabilités de décès
Bien que les modèles à composantes principales puissent être attrayants théoriquement, il reste à savoir s’ils sont attrayants en pratique. Pour en juger, il faut d’abord spécifier sur quelle dimension nous voulons mesurer la qualité de la performance d’un modèle de mortalité. Nous choisirons dans le cas présent l’erreur quadratique de prédiction qui se calcule comme
sur un horizon de h années. Afin d’obtenir cette statistique, chaque modèle est d’abord estimé sur la base des données disponibles de 1921 à 1961. À l’aide de chaque modèle, des prédictions de mortalité ![]() par âges (x) sont obtenus à des horizons (h) allant de 1 à 10 ans. On peut ensuite comparer ces prédictions aux réalisations
par âges (x) sont obtenus à des horizons (h) allant de 1 à 10 ans. On peut ensuite comparer ces prédictions aux réalisations ![]() . On répète la procédure annuellement, jusqu’en 2009-h, en augmentant l’échantillon utilisé pour l’estimation.
. On répète la procédure annuellement, jusqu’en 2009-h, en augmentant l’échantillon utilisé pour l’estimation.
Les deux tableaux suivants résument les résultats de ces prédictions basées sur six modèles possibles : le modèle Lee-Carter (LC), le modèle CBD (CBD), le modèle CBD où le modèle prédictif est un VAR (CBD–VAR), et les modèles avec une, deux et trois composantes principales (CP(1), CP(2), et CP(3), respectivement) et ce, pour les femmes (tableau 3) et pour les hommes (tableau 4)[15].
Le panneau supérieur des tableaux 3 et 4 rapporte la racine de la moyenne de l’erreur quadratique de prédiction
Cette statitistique donne un apperçu de l’erreur moyenne de prédiction à travers les temps, tous âges confondus. La RMSE du modèle le plus précis à chaque horizon est en caractère gras. Clairement, le modèle qui performe le mieux pour prédire les probabilités de décès à court et moyen terme, pour les femmes comme pour les hommes, est le modèle de base de CBD. La qualité du modèle CBD en comparaison des autres modèles est la plus marquante dans le cas des projections à plus d’un an pour les hommes. Le seul horizon sur lequel le modèle CBD n’est pas le plus performant pour les hommes est lorsqu’on projette sur un an.
D’ailleurs, la partie inférieure des tableaux 3 et 4 rapporte les statistiques de Diebold-Mariano (DM). Cette statistique est distribuée N(0,1) ; suivant cette distribution, les valeurs p (deux côtés) des statistiques obtenues sont rapportées entre parenthèses. Pour les hommes, les prévisions du modèle CBD sont presque systématiquement significativement plus précises que celles des autres modèles. Dans le cas des femmes, le modèle CBD est de manière générale celui qui fournit les prévisions les plus précises, mais les différences avec les modèles Lee-Carter et CP(1) ne sont pas statistiquement significatives.
Tableau 3
Prédictions hors échantillon des probabilités de décès : moyennes des erreurs carrées et tests de Diebold-Mariano pour les femmes canadiennes
Nous estimons les différents modèles en utilisant les données annuelles sur la mortalité des femmes canadiennes de 1921 à 1961. À l’aide de chaque modèle, des prédictions de mortalité  par âges (x) sont obtenus à des horizons (h) allant de 1 à 10 ans. La procédure est répétée annuellement en augmentant l’échantillon utilisé pour l’estimation.
par âges (x) sont obtenus à des horizons (h) allant de 1 à 10 ans. La procédure est répétée annuellement en augmentant l’échantillon utilisé pour l’estimation.
La racine de la moyenne des erreurs carrées,  , est rapportée en pourcentage pour chaque horizon dans la partie supérieure de la table. La partie inférieure de la table rapporte les statistiques de Diebold-Mariano (et leurs valeurs p, entre parathèses) obtenues en comparant les différents modèles au modèle de CDB sur la base des séries chronologiques d’erreurs quadratiques à chaque horizon,
, est rapportée en pourcentage pour chaque horizon dans la partie supérieure de la table. La partie inférieure de la table rapporte les statistiques de Diebold-Mariano (et leurs valeurs p, entre parathèses) obtenues en comparant les différents modèles au modèle de CDB sur la base des séries chronologiques d’erreurs quadratiques à chaque horizon,  . Lorsque la statistique de Diebold-Mariano est positive, la prédiction du modèle CBD est plus précise que celle du modèle considéré. L’inverse est vrai lorsque la statistique est négative.
. Lorsque la statistique de Diebold-Mariano est positive, la prédiction du modèle CBD est plus précise que celle du modèle considéré. L’inverse est vrai lorsque la statistique est négative.
Tableau 4
Prédiction hors échantillon : moyennes des erreurs carrées et tests de Diebold-Mariano pour les hommes canadiens
Reproduction de l’analyse présentée au tableau 3 en utilisant les données annuelles sur la mortalité des hommes canadiens de 1921 à 1961.
Un constat s’impose donc. Malgré l’attrait théorique de l’approche par composantes principales, la structure imposée aux facteurs CBD semble lui conférer un meilleur pouvoir prédictif en ce qui a trait aux probabilités de décès. Comme ces probabilités sont centrales au calcul de l’espérance des valeurs actualisées des rentes à payer par un fonds de pension, il faudra s’accommoder du fait que le modèle CBD ne distingue pas clairement quelles sont les sources de risques qui touchent le prix de produits dérivés sur l’évolution future de la longévité.
3. Gérer le risque de longévité pour la population et pour un fonds de pension
3.1 Le forward de longévité
Il existe plusieurs produits dans les marchés financiers qui permettent aux investisseurs de gérer leur risque soit en le tranférant à autrui, soit en l’assumant contre compensation. Un exemple des plus simples est celui des contrats à terme (forwards ci-après) sur un indice boursier, un taux d’intérêt ou un taux de change. Ces produits permettent de gérer le risque associé à des positions longues sur ces marchés, ou encore de prendre des positions spéculatives quant à la direction future de ces marchés. Or, contrairement aux contrats à terme sur titres financiers, les contrats à terme qui permettent de se couvrir contre des mouvements soudains de la mortalité ne sont que très peu transigés. Nous mettons en lumière certaines raisons pouvant potentiellement expliquer ce faible volume de transactions.
Plusieurs indices de mortalité ont été suggérés dans la dernière décennie. Théoriquement, chacun d’entre eux pourrait servir d’indice de référence sur lequel un forward pourrait être quoté et transigé de manière analogue aux forwards sur indices financiers. Dans l’ensemble l’indice qui a reçu le plus d’attention est probablement celui publié par LifeMetrics, une initiative de JP Morgan qui est maintenant chapeautée par la Life and Longevity Markets Association (LLMA)[16]. JP Morgan a suggéré deux types de forwards basés sur les indices LifeMetrics : les q-forwards et les S-forwards. Les q-forwards, par exemple, offre un paiement de la forme
où T est l’échéance du forward, ![]() est la réalisation du taux de mortalité sur lequel le forward est écrit et q̅x(t : T) est le « prix » forward d’échéance T sur lequel s’entendraient, au temps t, les contreparties. Conceptuellement, un q-forward pourrait être écrit sur une cohorte de gens de différents âges. Les S-forwards sont plutôt basés sur la survie de la cohorte, reliée à (
est la réalisation du taux de mortalité sur lequel le forward est écrit et q̅x(t : T) est le « prix » forward d’échéance T sur lequel s’entendraient, au temps t, les contreparties. Conceptuellement, un q-forward pourrait être écrit sur une cohorte de gens de différents âges. Les S-forwards sont plutôt basés sur la survie de la cohorte, reliée à (![]() ).
).
Un des problèmes de ces forwards vient peut-être justement du fait qu’ils sont écrits sur différentes cohortes, entrainant une multiplicité d’instruments. Dans un marché qui peine à démarrer, il pourrait être profitable de concentrer le volume de transaction sur un nombre restreint d’instruments permettant aux fonds de pensions, par exemple, de se couvrir contre les principales sources de risque auxquelles ils sont exposés. Par exemple, Chan, Li et Li (2014) suggère d’utiliser un indice basé sur la moyenne du logit des probabilités de décès
Notons que cette moyenne correspond au premier facteur CBD[17]. Comme tout fonds de pension détient naturellement une position longue sur la mortalité mesurée par K1, une position courte sur un K1-forward permettrait aux divers fonds de se couvrir contre une partie substantielle du risque de longévité.
Nous analyserons le prix forward du point de vue de la contrepartie de cette transaction, que nous nommerons « l’assureur ». Le gain de la position longue de l’assureur sur un K1-forward d’échéance T est
Si l’assureur n’était pas riscophobe, il suffirait que le gain espéré soit 0 pour que le forward soit juste pour les deux parties. Ainsi le prix forward au temps t devrait être : [18]
Comme l’assureur est riscophobe et ne peut couvrir sa position forward à l’aide d’une position sur le sous-jacent, nous aurons ![]() [19]. Cette inégalité signifie essentiellement que l’assureur exige un paiement supérieur à K1 (t : T) pour compenser pour le risque de sa position.
[19]. Cette inégalité signifie essentiellement que l’assureur exige un paiement supérieur à K1 (t : T) pour compenser pour le risque de sa position.
Ainsi, le forward contiendra une prime
où ![]() dénote l’espérance de K1(T) sous une mesure de probabilité ajustée pour le risque. Ainsi, E* tient compte des différentes sources de risque auxquelles l’assureur est exposé et du prix du risque associé à chacune de ces sources. Notons toutefois que E* dépendra du modèle choisi.
dénote l’espérance de K1(T) sous une mesure de probabilité ajustée pour le risque. Ainsi, E* tient compte des différentes sources de risque auxquelles l’assureur est exposé et du prix du risque associé à chacune de ces sources. Notons toutefois que E* dépendra du modèle choisi.
Nous nous concentrerons ici sur le cas d’un forward sur la longévité ayant une échéance d’un an. Ainsi, un fonds de pension qui voudrait se départir du risque d’amélioration non anticipée de l’espérance de vie à la retraite pourrait s’entendre avec une contrepartie de manière à ce que cette dernière assume le risque d’améliorations non anticipées des taux de survie sur l’année à venir. Le contrat venant à échéance à la fin de l’année, le fonds de pension recevra une compensation monétaire si l’espérance de vie s’est significativement améliorée (c’est-à-dire ![]() ) ou paiera sa contrepartie si l’espérance de vie s’est améliorée moins rapidement que prévue, ou si elle s’est détériorée[20]. Les parties pourront par la suite s’entendre sur une nouvelle position forward pour l’année qui suit.
) ou paiera sa contrepartie si l’espérance de vie s’est améliorée moins rapidement que prévue, ou si elle s’est détériorée[20]. Les parties pourront par la suite s’entendre sur une nouvelle position forward pour l’année qui suit.
Chaque année, pour chaque dollar de notionnel, le gain de l’assureur peut s’écrire comme suit :
où ![]() est un estimateur de l’espérance de K1(T) qui dépend du modèle choisi, tout comme
est un estimateur de l’espérance de K1(T) qui dépend du modèle choisi, tout comme ![]() . L’espérance de gain de l’assureur est donc :
. L’espérance de gain de l’assureur est donc :
Bref, si le modèle de prévision de la longévité utilisé par l’assureur est fortement négativement biaisé (![]() ), la prime de risque demandée sur la base de ce modèle pourrait être insuffisante pour garantir à l’assureur qu’il ne cumulera pas systématiquement des pertes. Or, la sous-estimation systématique de la longévité observée dans l’histoire récente laisse croire qu’un tel scénario n’est pas improbable.
), la prime de risque demandée sur la base de ce modèle pourrait être insuffisante pour garantir à l’assureur qu’il ne cumulera pas systématiquement des pertes. Or, la sous-estimation systématique de la longévité observée dans l’histoire récente laisse croire qu’un tel scénario n’est pas improbable.
3.2 Borne inférieure sur la prime de risque d’un modèle biaisé
Étant donné la supériorité du modèle CBD pour ce qui est des prédictions à différents horizons (cf. tableaux 3 et 4), nous nous concentrerons sur les primes de risque chargées par un assureur qui utiliserait ce modèle pour tarifer des forwards. Rappelons qu’à l’année , le fonds de pension et l’assureur peuvent observer
Sur la base de ces observations, ils peuvent estimer les paramètres du modèle prédictif
puis se baser sur ce modèle pour prévoir l’espérance de K(t +1) et, conséquemment, de l’indice K1(t +1).
Pour trouver le prix forward demandé par un agent riscophobe, il faudra tenir compte de l’évaluation de la prime de risque que cet agent demande pour l’assumer. Une approche simple est d’ajuster la distribution conditionnelle de K(t +1) (voir Wang, 2000; Boyer et Stentoft, 2013). En somme, alors que l’équation implique que ![]() , l’ajustement pour le risque est tel que
, l’ajustement pour le risque est tel que ![]() . Le vecteur
. Le vecteur  représente le prix de marché du risque et généralise en quelque sorte le concept du ratio de Sharpe :
représente le prix de marché du risque et généralise en quelque sorte le concept du ratio de Sharpe : ![]() est le prix associé à chaque « unité » de risque C. Comme il y a deux facteurs imparfaitement corrélés dans le modèle, il doit y avoir deux sources de risque, dont λ1 et λ2 sont leur prix de marché respectifs.
est le prix associé à chaque « unité » de risque C. Comme il y a deux facteurs imparfaitement corrélés dans le modèle, il doit y avoir deux sources de risque, dont λ1 et λ2 sont leur prix de marché respectifs.
En marché incomplet, λ1 et λ2 sont habituellement estimées à l’aide des prix passés de produits dérivés qui dépendent des différentes sources de risque. Étant donné l’absence de liquidité sur les marchés de forward sur longévité – et donc de prix historiques relativement peu biaisés – on se propose plutôt ici d’extraire une borne inférieure pour la prime de risque demandée par l’assureur.
Considérons un assureur qui serait conscient du biais systématique du modèle CBD, mais qui serait autrement indifférent au risque de mortalité. Ne désirant pas encourir systématiquement les pertes reliées au biais du modèle cet assureur pourrait demander, sous les hypothèses du modèle, une prime forward qui soit tout juste suffisante pour couvrir ce biais, mais sans plus. Conceptuellement, cette approche est strictement équivalente à la recherche d’un prix de marché du risque tel que l’espérance de gain dans l’équation oit égale à zéro. Ainsi, la prime obtenue ne compensant que pour le biais du modèle, elle représentera une borne inférieure à la prime que pourrait demander un assureur riscophobe.
Le graphique 4 illustre le comportement dans le temps de la borne inférieure de la prime forward (en dollars) ayant une échéance d’une année rédigé sur K1(t) dont le notionnel est de 100 $. Le panneau du haut (bas) illustre le comportement de la prime forward dans le temps pour les femmes (hommes). Nous ne représentons les primes forward que pour les années 1960 à 2010 puisque les premières décennies sont utilisées pour estimer les premières valeurs des paramètres du modèle CBD.
Graphique 4
Primes forward sur l’indice K1
Prime forward 1 an en utilisant CBD - Femmes
Prime forward 1 an en utilisant CBD - Hommes
Évolution des primes obtenues en utilisant le modèle CBD pour des forwards de maturité d’un an sur l’indice K1 pour les femmes et pour les hommes canadiens. Le tracé marqué de x est obtenue en supposant que le prix de marché du risque associé au deuxième facteur CBD est nul (2 = 0) et en recherchant le prix de marché du risque 1 tel que l’assureur aurait réalisé un profit nul en prenant séquentiellement position sur ce forward entre 1961 et 2008. Ce graphique rapporte aussi des tracés correspondants à des hypothèses alternatives sur la relation entre les prix de marché sur les deux facteurs λ1 et λ2; ces tracés ne sont à toute fin pratique pas visibles parce que la seconde source de risque (touchée par λ2) n’a pas d’impact sur K1.
Il est clair dans le graphique précédent que la prime forward pour les femmes est bien inférieure à celle pour les hommes et ce, pour un même niveau de notionnel. Nous constatons également que la valeur de λ2 n’a aucun impact sur les primes forward. En effet, la structure triangulaire supérieure de C est telle que
Ainsi, le premier facteur CBD sous-jacent au contrat forward qui nous intéresse, ne dépend que de la première source de risque. D’un côté, cette propriété à l’avantage de simplifier l’identification des prix de marchés du risque. Nous avons noté précédemment que le modèle CBD surperformait nettement le modèle à un facteur de Lee-Carter et ce, malgré la très forte corrélation entre le facteur de Lee-Carter et le premier facteur CBD. Le second facteur CBD est donc important pour décrire adéquatement l’évolution des probabilité de décès dans le temps. Or, comme la corrélation entre ce second facteur et le premier est (évidemment) imparfaite, il s’ensuit qu’une seconde source de risque d’importance touche directement les fonds de pension. Conséquemment, un contrat forward sur K1(t) uniquement ne peut permettre à un fonds de pension de se couvrir adéquatement contre cette seconde source de risque.
3.2 La gestion du risque de longévité pour un fonds de pension
L’exercice précédent illustre pourquoi un forward sur l’indice K1 ne suffirait, à lui seul, à un fonds de pension de parfaitement couvrir son risque de longévité. Une autre considération d’importance lorsque l’on considère une couverture à l’aide de forward est le risque de base, que nous définissons comme le risque que le produit de gestion que nous nous procurons pour limiter notre exposition à une variation de la longévité ait une corrélation imparfaite (voire nulle) avec notre exposition au risque. En d’autres termes, le risque de base est le risque que notre outil de gestion du risque ne fonctionne pas pour gérer le risque.
Pour des fins d’analyse et pour simplifier le problème sans en toucher l’essentiel, supposons un fonds de pension ne versant des rentes de retraite qu’une fois par année à la fin de l’année. Supposons aussi que le même montant P est versé à tous les rentiers. En début d’année, la valeur actualisée des primes totales (PTt) que devra verser un tel fonds à la fin de l’année est donnée par
où Nx est le nombre de pensionnaires d’âge x et VA(P) est la valeur actualisée de P. La prime moyenne par individu (PM) sera ainsi
où ![]() est la proportion des pensionnaires d’âge x. Le fonds a donc une position courte sur
est la proportion des pensionnaires d’âge x. Le fonds a donc une position courte sur ![]() plutôt qu’une position longue sur la moyenne équipondérée du logit de probabilités de décès. Ainsi, le fonds s’expose à un risque de base s’il se couvre à l’aide de forwards sur K1.
plutôt qu’une position longue sur la moyenne équipondérée du logit de probabilités de décès. Ainsi, le fonds s’expose à un risque de base s’il se couvre à l’aide de forwards sur K1.
De plus, un fonds de pension donné peut avoir une population de rentiers aux caractéristiques particulières. Par exemple, considérons un fonds qui ne compterait que des rentiers présentement âgés entre 65 et 74 ans et dont le poids démographique correspondrait celui de la population canadienne. Ce fonds préfèrerait probablement se couvrir à l’aide d’un forward écrit sur
où les ![]() représentent la proportion des 65-74 ans agés de x années exactement[21]. L’évolution des indices K1(t) et Q(t) pour les hommes et les femmes est représentée dans les panneaux 1 et 2 du graphique 5. Le troisième panneau dans le graphique 5 donne les poids associés à chaque âge dans le calcul de l’indice Q(t).
représentent la proportion des 65-74 ans agés de x années exactement[21]. L’évolution des indices K1(t) et Q(t) pour les hommes et les femmes est représentée dans les panneaux 1 et 2 du graphique 5. Le troisième panneau dans le graphique 5 donne les poids associés à chaque âge dans le calcul de l’indice Q(t).
Graphique 5
Indices K1 et Q
Indice K
Indice Q
Poids associés à Q (%)
Évolution au Canada, au cours des années 1921 à 2009, de l’indice ![]() , et
, et ![]() , pour les hommes (
, pour les hommes (![]() ) et pour les femmes (
) et pour les femmes (![]() ). Les poids wx associés à l’indice Q(t) sont présentés en pourcentage.
). Les poids wx associés à l’indice Q(t) sont présentés en pourcentage.
Les indices K1(t) et Q(t) sont de magnitudes comparables (au signe près) et sont fortement corrélés; à 98,0 % chez les femmes et à 98,8 % chez les hommes.
En reprenant l’analyse de la section précédente, nous extrayons les bornes inférieures sur les primes de risques que demanderait un assureur pour vendre un forward sur Q(t). De manière similaire à ce que nous avons présenté au graphique 5, le graphique 6 illustre le comportement dans le temps de la prime forward (en dollars)d’un contrat écrit sur Q(t) dont le notionnel est de 100 $. Le panneau du haut (bas) illustre le comportement de la prime forward dans le temps pour les femmes (hommes).
En comparaison avec les résultats que nous avons présentés dans le graphique 4, ceux du graphique 6 mettent en exergue quelques problèmes importants quand vient le temps de trouver la prime adéquate d’un contrat forward sur Q(t). Premièrement, les primes forward sur Q(t) sont largement plus grandes que sur K1(t). Alors que nous avions des primes forward sur l’indice K1(t) d’environ 0,54 $ (avec λ2 = 0) pour les femmes en 1960, les primes forward sur l’indice Q(t) sont de 15 $. Pour les hommes en 1960, la prime forward sur l’indice K1(t) est de 1,15 $ (avec λ2 = 0) et celle sur l’indice Q(t) est de 32 $. Ces différences sont significatives!
D’autre part, nous observons ici des primes plus élevées pour les femmes que pour les hommes, contrairement à ce à quoi nous aurions pu nous attendre étant donné les résultats illustrés dans le graphique 5. Ce résultat est attribuable à l’utilisation d’un indice qui n’est pas équipondéré. Il met ainsi en lumière l’hétérogénéité des erreurs de prédictions du modèle CBD. En effet, les erreurs sont relativement plus influencées par la prédiction des probabilités de décès des jeunes femmes retraitées qui ont évidemment une pondération plus importante dans l’indice Q, qui est pondéré en fonction de la population canadienne réelle, que dans l’indice K1, qui équipondère toutes les tranches de la population canadienne. Chez les hommes, les erreurs sont relativement plus prononcées chez les vieux retraités, qui sont exclus de l’indice Q puisqu’il ne prend en considération que les hommes âgés de 65 à 75 ans.
Enfin, le prix de marché du risque associé au second facteur, λ2, joue un rôle non négligeable. En effet, dépendemment du prix du risque associé au second facteur, la prime de risque peut pratiquement doubler. Pour mieux comprendre la relation entre λ1 et λ2, il faudrait les extraires de prix de transaction réelles et fiables. Toutefois, remarquons qu’une baisse de ce second facteur serait perçu comme une bonne nouvelle pour le fonds, contrairement à une baisse du premier facteur. Ainsi, on peut présumer que λ2 sera négatif, contrairement à λ1 et que, par conséquent, les primes se trouveraient sous la ligne foncée plutôt qu’au-dessus.
L’exercice que nous venons de faire laisse tout de même présager que le risque de modèle et le risque de base sont considérables pour les fonds de pension. En effet, en marché incomplet, le choix du modèle a un impact direct sur l’estimation des prix de marché du risque. Ceux-ci ont, à leur tour, un impact significatif sur les primes à payer. D’autre part, les primes Q-forwards sont nettement plus élevées que les primes K1-forwards. Ainsi, si les marchés n’offraient que des K1-forward comme outils de couverture, le fonds de pension paierait des primes moins élevées, mais au risque de ne couvrir que partiellement le risque auquel il s’expose.
Graphique 6
Primes forward sur l’indice Q
Prime forward 1 an en utilisant CBD - Femmes
Prime forward 1 an en utilisant CBD - Hommes
Évolution des primes obtenues en utilisant le modèle CBD pour des forwards de maturité d’un an sur l’indice Q pour les femmes et pour les hommes canadiens. Le tracé marqué de x est obtenue en supposant que le prix de marché du risque associé au deuxième facteur CBD est nul (λ2 = 0) et en recherchant le prix de marché du risque λ1 tel que l’assureur aurait réalisé un profit nul en prenant séquentiellement position sur ce forward entre 1961 et 2008. Les autres tracés correspondent à des hypothèses alternatives sur la relation entre les prix de marché sur les deux facteurs, λ1 et λ2.
En conclusion, rappelons que les primes rapportées par les graphiques 4 et 6 ne sont que des bornes inférieures aux primes que chargerait un assureur riscophobe. En effet, nous avons considéré ici un assureur qui, bien que conscient du biais systématique du modèle CBD, est indifférent au risque de mortalité. Cet assureur ne demande donc qu’une prime qui soit tout juste suffisante pour couvrir le biais dans le modèle CBD, mais sans plus. Étant donné le niveau de ces bornes inférieures, il est fort probable que les primes demandées par un assureur riscophobe dépasseraient la volonté de payer d’un fonds de pension.
Conclusion
Dans des travaux précédents (voir Boyer et al., 2014), nous avons calculé qu’un fonds de pension au Canada serait prêt à payer environ 5 % de la valeur présente de son passif actuariel pour s’assurer que dans 99 % des cas le fonds de pension n’aura pas sous-estimé l’âge de décès de ses rentiers. Il est clair que la prime dépend de la structure d’âge des membres du fonds de pension et de la représentation des sexes. La prime dépend également du pays de domicile du fonds de pension (ou du pays d’origine de ses participants) de telle sorte que la prime de 5 % que nous sommes capables de calculer au Canada et aux États-Unis monte à 10 % en Europe de l’Ouest et au Japon. Ces pourcentages offrent une borne minimale par rapport aux taux qui ont été payés dernièrement par les entreprises qui ont opté pour se débarrasser complètement de leur responsabilité envers leur fonds de pension à prestations déterminées (ce qu’on appelle communément un « buy-out »). Selon un rapport récent de Mercer[22], le coût moyen de se départir complètement du risque associé aux rentiers des fonds de pension est d’environ 14 % (cette prime de risque varie de 24 % au Royaume-Uni à 4 % au Canada).
Il est vrai que la popularité des fonds de pension à prestations déterminées dans le secteur privé est en chute constante aux États-Unis et au Canada depuis une vingtaine d’années (les régimes à prestations déterminées demeurent particulièrement populaires dans le secteur public et parapublic) au profit de fonds de pension à contributions déterminée. Contrairement aux fonds à prestations déterminées où l’employeur s’engage à verser une rente de retraite aux employés au moment où ceux-ci la prenne, ce sont les employées qui deviennent reponsables d’accumuler suffisament de richesses pour la retraite dans le cas où le fonds est à cotisations déterminées.
En échangeant un paiement futur incertain aux futurs rentiers contre un paiement immédiat certain aux employés actuels les employeurs ne font pas disparaitre le risque de longévité. Ainsi le changement dans le financement de la retraite des particuliers génèrera une hausse de la demande pour les rentes viagères, ce qui implique que les compagnies d’assurance-vie vont devoir porter une attention particulière au risque de longévité. En d’autres termes, le passage de fonds à prestations déterminées à fonds à cotisations déterminées ne fait pas disparaitre le risque de longévité; il est vrai que l’employeur se débarrasse du risque de placement et de longévité, mais ce sont les employés qui doivent alors les assumer puisqu’ils deviennent alors responsables de faire fructifier les sommes versées par l’employeur pour bâtir un capital suffisant à la retraite et de planifier adéquatement le retrait de ces sommes à la retraite (ou acheter une rente viagère auprès d’un assureur qui assume alors le risque de longévité).
La question qu’il faut alors se poser comme économistes financiers est s’il existe un moyen de gérer ce risque de longévité pour les entreprises, qui offrent à leurs employés un fonds de pension à prestations déterminées, ou pour les compagnies d’assurances qui vendent des rentes viagères aux individus qui prennent leur retraite? Quelle est la conséquence de ne pas gérer le risque de longévité pour les entreprises canadiennes alors que ce risque est particulièrement élevé pour les entreprises qui offrent à leurs employés un régime de pension à prestations déterminées? Dans ce cas, non seulement l’employeur assume-t-il le risque de placement pour capitaliser les sommes nécessaires pour verser les rentes de retraite, il assume également le risque que la population couverte par le fonds de pension vive au-delà (ou en deça, mais c’est moins dommageable) de ce qui avait été anticipé. Et bien que le risque de placement puisse être largement diversifié en donnant des mandats à plusieurs gestionnaires et en diversifiant de manière intertemporelle (c’est-à-dire en ayant des bonnes années suivies de moins bonnes années), il n’existe pratiquement pas d’outils financiers qui permettraient de gérer le risque de longévité tel que nous l’entendons ici.
Les résultats que nous avons présentés dans ce document suggèrent que même si on s’entendait sur le modèle statistique offrant les meilleurs prédictions de l’espérance de vie et de la longévité de la population canadienne, son imprécision pourrait être tel que la prime à payer pour transférer ce risque à une entité qui est en meilleure position pour l’assumer est bien au-delà de la volonté à payer de fonds de pension. Il est donc clair que davantage de recherche en démographie et en économie des populations sont encore nécessaires pour réduire le risque de modèle. D’ici là, il nous semble improbable que l’on puisse correctement asseoir les bases d’un marché financer qui permettrait de gérer le risque de longévité d’une manière dynamique, fluide et profitable pour toutes les parties concernées.
Appendices
Remerciements
Cette recherche est financée par le Conseil de recherche en sciences humaines du Canada, l’Institut de la finance structurée et des instruments dérivés de Montréal et le CIRANO.
Notes
-
[1]
Malthus (1992) en parlait même à la fin du XVIIIe siècle dans un ouvrage initialement publié en 1798.
-
[2]
Un rapport de la Bank for International Settlement (2013) discute en détail de la situation.
-
[3]
Plusieurs produits dérivés de la longévité ont déjà été suggérés, mais la longévité à proprement parler n’est pas et ne sera probablement jamais transigée de manière dynamique. Dit autrement, si jamais il arrivait que les produits dérivés de la longévité soient transigés activement, ce ne sera certainement que dans le cadre d’un marché financier incomplet.
-
[4]
Il est particulièrement difficile de faire des prévisions à partir de ces modèles. Tout d’abord, les facteurs de décès doivent être restreints à ceux qui sont possiblement prévisibles. Idéalement, ils devraient aussi être indépendants, ce qui est rarement le cas. Il faut également avoir accès à suffisamment de données sur ces facteurs pour obtenir une certaine robustesse des résultats. Un dernier problème se pose enfin, et non le moindre : il faut déterminer comment une évolution du facteur va impacter concrètement le taux de mortalité.
-
[5]
Le système d’équations en est tel que k n’est identifié qu’à une transformation linéaire près (Lee et Carter, 1992). Il est donc d’usage de normaliser ce système en imposant
 et
et  .
. -
[6]
Bien que le modèle Lee-Carter ait été développé sur les données américaines, Lee et Nault (1993) ont montré qu’il s’applique aussi bien aux données canadiennes (voir aussi Denton et al., 2006).
-
[7]
Notons que les équations (1) et (2) pourraient aussi être considérées respectivement comme les équations d’observation et de transition d’un système linéaire qui pourrait être estimé à l’aide d’un filtre de Kalman. Hyndman et Ullah (2007) et De Jong et Tickle (2006) ainsi que Hyndman et Ullah (2007) proposent des extensions en ce sens. Dans le cadre de notre étude, toutefois, nous nous limitons à l’estimation classique basée sur la composante principale des séries de log-mortalité.
-
[8]
Notre estimation du modèle de Lee-Carter est basée sur les probabilités de décès (
 ) au Canada publiées par http://www.mortality.org. La base de données contient aussi les données brutes de mortalité (
) au Canada publiées par http://www.mortality.org. La base de données contient aussi les données brutes de mortalité ( ). Or, certains raffinements sont apportés à
). Or, certains raffinements sont apportés à  pour en améliorer la fiabilité, de telle sorte que la relation
pour en améliorer la fiabilité, de telle sorte que la relation  ne tient pas exactement dans les données brutes. Pour nous assurer de la cohérence des modèles que nous estimons, nous utilisons donc les probabilités de décès transformées,
ne tient pas exactement dans les données brutes. Pour nous assurer de la cohérence des modèles que nous estimons, nous utilisons donc les probabilités de décès transformées,  , pour estimer le modèle Lee-Carter. Dowd, Cairns, Blake, Coughlan, Epstein et Khalaf-Allah (2010) procède inversement en utilisant les données brutes de mortalités mx(t) pour estimer le modèle de Lee-Carter et
, pour estimer le modèle Lee-Carter. Dowd, Cairns, Blake, Coughlan, Epstein et Khalaf-Allah (2010) procède inversement en utilisant les données brutes de mortalités mx(t) pour estimer le modèle de Lee-Carter et  pour estimer les modèles basés sur
pour estimer les modèles basés sur  .
. -
[9]
Ici, par Choleski on entend la matrice triangulaire supérieure telle que
 , où
, où  est la matrice de covariance du système.
est la matrice de covariance du système. -
[10]
Il est bon de noter que (i) le log de Lee-Carter n’est pas beaucoup plus intuitif et (ii) pour les valeurs d’erreurs qui nous intéressent, la distorsion de la distribution des erreurs est négligeable.
-
[11]
Par construction chaque composante a une moyenne nulle, ce qui explique la valeur de zéro au milieu de l’axe vertical dans chacun des panneaux.
-
[12]
Voir Cairns et al. (2009), Dowd, Blake et Cairns (2010) et Chan, Li et Li (2014).
-
[13]
Les données ici sont les données moyennes pour l’ensemble de la population et ne tiennent pas compte des spécificités de chaque individu (fumeur ou non, antécédents médicaux, poids et indice de masse corporelle) qui chercherait à obtenir de telles rentes.
-
[14]
Étant donné le manque de données après l’âge de 105 ans, on présume pour le calcul de ses primes que tous les retraités décèdent avant leur 106e anniversaire. Ces primes sont donc légèrement conservatrices.
-
[15]
Pour le modèle CP(n), basé sur les n premières composantes, nous utilisons le modèle prédictif suivant :

où, pour le modèle CP(n), les matrices B et C sont diagonales n × n. Bien que les composantes principales soient orthogonales au temps t, leurs dynamiques pourraient être interreliées. Toutefois, nous avons testé un modèle prédictif où les matrices B et C ne sont pas diagonales et les prédictions résultantes sont systématiquement moins précises.
-
[16]
La LLMA est un regroupement d’institutions financières qui ont un intérêt à voir émerger un marché crédible et liquide de la longévité : Aviva, AXA, Deutsche Bank, J.P. Morgan, Munich Re, Legal & General, Morgan Stanley, Pension Corporation, Prudential PLC, RBS, Swiss Re et UBS.
-
[17]
En fait, Chan, Li et Li (2014) sont d’avis que les indices de longévité gagneraient à être extraits de modèles et c’est pourquoi ils suggèrent d’écrire des produits dérivés sur les deux facteurs du modèle CBD. Bien que nous ne soyons pas convaincus que d’ancrer un indice dans un modèle soit nécessairement une approche pérenne, il n’en demeure pas moins que le premier facteur CBD n’est qu’une simple moyenne, un concept relativement peu dépendant du modèle.
-
[18]
Il est à noter que, tant que la probabilité de décès moyenne sera inférieure à 50 %, cet indice sera négatif. Ainsi, en pratique, K1(t) sera systématiquement négatif. Les prix forwards associés le seront donc aussi; la mortalité est un passif et non un actif.
-
[19]
Si l’indice K1 sous-jacent au forward était transigé, la relation de cash & carry usuelle s’appliquerait et on obtiendrait
 . Ici, le sous-jacent n’est pas transigé.
. Ici, le sous-jacent n’est pas transigé. -
[20]
En pratique, dans une transaction de gré à gré, l’assureur pourrait exiger la valeur actualisée de la prime au début de l’année, puis dédommager le fonds de pension si
 .
. -
[21]
Nous dénoterons pour le reste du document
 , où
, où  représente le nombre de canadiens d’âge x en 2009.
représente le nombre de canadiens d’âge x en 2009. -
[22]
http://www.mercer.ca/content/mercer/north-america/ca/fr/insights/point/2014/mercer-canada-pension-buyout-index.html, en date du 29 octobre 2014.
Bibliographie
- Bank for International Settlement (2013), « Longevity Risk Transfer Markets : Market Structure, Growth Drivers and Impediments, and Potential Risks », Rapport du Basel Committee on Banking Supervision.
- Biffis, E. (2005), « Affine Processes for Dynamic Mortality and Actuarial Valuation », Insurance : Mathematics and Economics, 37 : 443-468.
- Bongaarts, J. (2004), « Population Aging and the Rising Cost of Public Pensions », Population and Development Review, 30 : 1-23.
- Booth, H. et L. Tickle (2008), « Mortality Modelling and Forecasting : A Review of Methods », The Australian Demographic and Social Research Institute, document de travail no 3.
- Boyer, M.M., J. Mejza et L. Stentoft (2014), « Measuring Longevity Risk for a Canadian Public Pension Fund », Risk Management and Insurance Review, 17 : 37-59.
- Boyer, M.M. et L. Stentoft (2013), « If We Can Simulate it, We Can Insure it : An Application to Longevity Risk Management », Insurance : Mathematics and Economics, 52 : 35-45.
- Cairns, A.J.G., D. Blake, et K. Dowd (2006a), « Pricing Death : Frameworks for the Valuation and Securitization of Mortality Risk », ASTIN Bulletin, 36 : 79-120.
- Cairns, A.J.G., D. Blake, et K. Dowd (2006b), « A Two-Factor Model for Stochastic Mortality with Parameter Uncertainty : Theory and Calibration », Journal of Risk and Insurance, 73 : 687-718.
- Cairns, A.J.G., D. Blake, K. Dowd, G.D. Coughlan, D. Epstein et M. Khalaf-Allah (2011), « Mortality Density Forecasts : An Analysis of Six Stochastic Mortality Models », Insurance : Mathematics and Economics, 48 : 355-367.
- Cairns, A.J.G., D. Blake, K. Dowd, G.D. Coughlan, D. Epstein, A. Ong et I. Balevich (2009), « A Quantitative Comparison of Stochastic Mortality Models Using Data From England and Wales and the United States », North American Actuarial Journal, 13 : 1-35.
- Chan, W.S., J.S.H. Li et J. Li (2014), « The CBD Mortality Indexes : Modeling and Applications », Université de Waterloo, Document de travail.
- Dahl, M. (2004), « Stochastic Mortality in Life Insurance : Market Reserves and Mortality-linked Insurance Contracts », Insurance : Mathematics and Economics, 35 : 113-136.
- De Jong P. et L. Tickle (2006), « Extending Lee-Carter Mortality Forecasting », Mathematical Population Studies, 13 : 1-18.
- Denton, F.T., C.H. Feaver et B.G. Spencer (2005), « Time Series Analysis and Stochastic Forecasting : An Econometric Study of Mortality and Life Expectancy », Journal of Population Economics, 18 : 203-227.
- Dowd, K., D. Blake et A.J.G. Cairns (2010), « Facing Up to Uncertain Life Expectancy : The Longevity Fan Charts », Demography, 47 : 67-78.
- Dowd, K., A.J.G. Cairns, D. Blake, G.D. Coughlan, D. Epstein, et M. Khalaf-Allah (2010), « Evaluating the Goodness of Fit of Stochastic Mortality Models », Insurance : Mathematics and Economics, 47 : 255-265.
- Gaille S. (2012), « Forecasting Mortality : When Academia Meets Practice », European Actuarial Journal, 2 : 49-76.
- Gaille, S. et M. Sherris (2012), « Causes-of-Death Mortality : What Can Be Learned from Cointegration », document de travail.
- Gompertz, B. (1825), « On the Nature of the Function of the Law of Human Mortality », Philosophical Transactions of the Royal Society of London, 115, : 513-583.
- Hanewald, K. (2009), « Mortality Modeling : Lee-Carter and the Macroeconomy », SFB 649 Discussion Paper.
- Heligman, L. et J. H. Pollard (1980), « The Age Pattern of Mortality », Journal of the Institute of Actuaries, 107 : 49-80.
- Human Mortality Database, [base de données en ligne]. http://www.mortality.org/.
- Hyndman R., J. et M. S. Ullah (2007), « Robust Forecasting of Mortality and Fertility Rates : A Functional Data Approach », Computational Statistics and Data Analysis, 51 : 4942-4956.
- Lee, R.D. et F. Nault (1993), « Modeling and Forecasting Provincial Mortality in Canada », World Congress of the IUSSP, Montréal, Canada.
- Lee, R.D et L. Carter (1992), « Modeling and Forecasting U.S. Mortality », Journal of the American Statistical Association, 87 : 659-671.
- Malthus, T.R. (1992), Essai sur le principe de population, Paris, Flammarion. Ouvrage initialement publié en anglais en 1798 sous le titre An Essay on the Principle of Population.
- Manton, K.G., C.H. Patrick et E. Stallard (1980), « Mortality Model Based on Delays in Progression of Chronic Diseases : Alternative To Cause Elimination Model », Public Health Reports, 95 : 580-588.
- Manton, K.G., J.M. Wrigley, H.J. Cohen et M.A. Woodburgy (1991), « Cancer Mortality, Aging, and Patterns of Comorbidity in the United States : 1968 to 1986 », Journal of Gerontology, 46 : 225-234.
- Olivieri, A. (2001), « Uncertainty in Mortality Projections : An Actuarial Perspective », Insurance : Mathematics and Economics, 29 : 231-245.
- Planchet, F., M. Juillard et L. Faucillon (2006), « Quantification du risque systématique de mortalité pour un régime de rentes en cours de service », Assurance et gestion des risques 75.
- Planchet, F. et V. Lelieur (2007), « Utilisation des méthodes de Lee-Carter et Log-Poisson pour l’ajustement de tables de mortalité dans le cas de petits échantillons », Bulletin Français d’Actuariat, 8 : 118-146.
- Renshaw, A.E. et S. Haberman (2006), « Cohort-Based Extension to the Lee-Carter Model for Mortality Reduction Factors », Insurance : Mathematics and Economics, 38 : 556-570.
- Rechel, B., E. Grundy, J.M. Robine, J. Cylus, J.P. Mackenbach, C. Knai et M. McKee (2013), « Ageing in the European Union », The Lancet, 381 : 1312-1322.
- Robine J.M. et J.P. Michel (2004), « Looking Forward to a General Theory on Population Aging », Journal of Gerontoly, 59 : 590-597.
- Sharrow, D.J. (2013), « Modeling the Age Pattern of Human Mortality : Mathematical and Tabular Representations of the Risk of Death », Thèse de doctorat, University of Washington.
- Thatcher, A. R. (1987), « Mortality at the Highest Ages », Journal of the Institute of Actuaries, 114 : 327-338.
- Thatcher, A. R. (1990), « Some Results on the Gompertz and Heligman and Pollard Laws of Mortality », Journal of the Institute of Actuaries, 117 : 135-149.
- Wang, S. (2000), « A Class of Distorsion Operators for Pricing Financial and Insurance Risks », The Journal of Risk and Insurance, 67 : 15-36.
- Wilmoth, J.R. (1995), « Are Mortality Projections Always More Pessimistic When Disaggregated by Cause of Death? », Mathematical Populations Studies, 5 : 293-319.
List of figures
Femmes
Hommes
Évolution au Canada de la probabilité de décès, au cours des années 1921 à 2009, pour les femmes et les hommes de différents âges. Autant chez les hommes que chez les femmes, le taux de mortalité a décru significativement au cours du dernier siècle. En plus de cette tendence à la baisse, ce graphique illustre aussi une autre régularité empirique : l’amélioration de la longévité est plus marqué aux âges avancés (ici 85 ans) qu’elle ne l’est à des âges moins avancés (ici 65 ans).
Facteur Lee-Carter
Premier Facteur CBD
Deuxième Facteur CBD
Évolution au Canada, au cours des années 1921 à 2009, du facteur sous-jacent au modèle de Lee-Carter et des facteurs du modèle CBD, K1 (·) et K2 (·) au Canada, pour les hommes (![]() ) et pour les femmes (
) et pour les femmes (![]() ) de 55 à 105 ans.
) de 55 à 105 ans.
Première Composante Pricipale
Deuxième Composante Pricipale
Troisième Composante Pricipale
Évolution au Canada, au cours des années 1921 à 2009, des trois composantes principales du logit de la mortalité— ![]() —pour ; pour les hommes (
—pour ; pour les hommes (![]() ) et pour les femmes (
) et pour les femmes (![]() ) de 55 à 105 ans.
) de 55 à 105 ans.
Prime forward 1 an en utilisant CBD - Femmes
Prime forward 1 an en utilisant CBD - Hommes
Évolution des primes obtenues en utilisant le modèle CBD pour des forwards de maturité d’un an sur l’indice K1 pour les femmes et pour les hommes canadiens. Le tracé marqué de x est obtenue en supposant que le prix de marché du risque associé au deuxième facteur CBD est nul (2 = 0) et en recherchant le prix de marché du risque 1 tel que l’assureur aurait réalisé un profit nul en prenant séquentiellement position sur ce forward entre 1961 et 2008. Ce graphique rapporte aussi des tracés correspondants à des hypothèses alternatives sur la relation entre les prix de marché sur les deux facteurs λ1 et λ2; ces tracés ne sont à toute fin pratique pas visibles parce que la seconde source de risque (touchée par λ2) n’a pas d’impact sur K1.
Indice K
Indice Q
Poids associés à Q (%)
Évolution au Canada, au cours des années 1921 à 2009, de l’indice ![]() , et
, et ![]() , pour les hommes (
, pour les hommes (![]() ) et pour les femmes (
) et pour les femmes (![]() ). Les poids wx associés à l’indice Q(t) sont présentés en pourcentage.
). Les poids wx associés à l’indice Q(t) sont présentés en pourcentage.
Prime forward 1 an en utilisant CBD - Femmes
Prime forward 1 an en utilisant CBD - Hommes
Évolution des primes obtenues en utilisant le modèle CBD pour des forwards de maturité d’un an sur l’indice Q pour les femmes et pour les hommes canadiens. Le tracé marqué de x est obtenue en supposant que le prix de marché du risque associé au deuxième facteur CBD est nul (λ2 = 0) et en recherchant le prix de marché du risque λ1 tel que l’assureur aurait réalisé un profit nul en prenant séquentiellement position sur ce forward entre 1961 et 2008. Les autres tracés correspondent à des hypothèses alternatives sur la relation entre les prix de marché sur les deux facteurs, λ1 et λ2.
List of tables
Tableau 1
Corrélations entre les différents facteurs
La partie triangulaire inféreure présente la corrélation entre les facteurs des modèles de Lee-Carter (LC) et CBD (K1 et K2) et les trois composantes principales du logit de la mortalité pour les femmes canadiennes entre 1921 et 2009. La partie triangulaire supérieure présente les corrélations correspondantes pour les hommes.
Tableau 2
Primes pour une annuité de 100$
Primes correspondant à une annuité de 100 $ pour un nouveau retraité de 65 ans, basées sur les différents modèles estimés à l’aide des données canadiennes de mortalité de 1921 à 2009. Un taux de 6,75 % est utilisé par plusieurs fonds de pension. Le rapport d’Amours suggère plutôt d’utiliser un taux provenant d’indices d’obligations de très grandes qualités. Les taux de 5,98 % et 4,89 % correspondent aux rendements de tels indices sur obligations corporatives et gouvernementales, respectivement, depuis novembre 2006. Plus précisément, les indices utilisés sont les suivants : (i) FTSE TMX Canada All Corporate Bond Index, (ii) FTSE TMX Canada All Government Bond Index.
Tableau 3
Prédictions hors échantillon des probabilités de décès : moyennes des erreurs carrées et tests de Diebold-Mariano pour les femmes canadiennes
Nous estimons les différents modèles en utilisant les données annuelles sur la mortalité des femmes canadiennes de 1921 à 1961. À l’aide de chaque modèle, des prédictions de mortalité  par âges (x) sont obtenus à des horizons (h) allant de 1 à 10 ans. La procédure est répétée annuellement en augmentant l’échantillon utilisé pour l’estimation.
par âges (x) sont obtenus à des horizons (h) allant de 1 à 10 ans. La procédure est répétée annuellement en augmentant l’échantillon utilisé pour l’estimation.
La racine de la moyenne des erreurs carrées,  , est rapportée en pourcentage pour chaque horizon dans la partie supérieure de la table. La partie inférieure de la table rapporte les statistiques de Diebold-Mariano (et leurs valeurs p, entre parathèses) obtenues en comparant les différents modèles au modèle de CDB sur la base des séries chronologiques d’erreurs quadratiques à chaque horizon,
, est rapportée en pourcentage pour chaque horizon dans la partie supérieure de la table. La partie inférieure de la table rapporte les statistiques de Diebold-Mariano (et leurs valeurs p, entre parathèses) obtenues en comparant les différents modèles au modèle de CDB sur la base des séries chronologiques d’erreurs quadratiques à chaque horizon,  . Lorsque la statistique de Diebold-Mariano est positive, la prédiction du modèle CBD est plus précise que celle du modèle considéré. L’inverse est vrai lorsque la statistique est négative.
. Lorsque la statistique de Diebold-Mariano est positive, la prédiction du modèle CBD est plus précise que celle du modèle considéré. L’inverse est vrai lorsque la statistique est négative.
Tableau 4
Prédiction hors échantillon : moyennes des erreurs carrées et tests de Diebold-Mariano pour les hommes canadiens



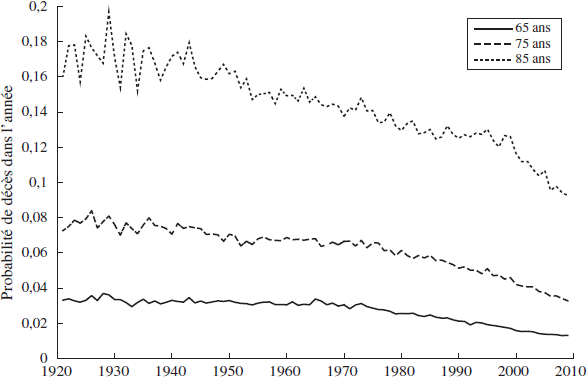

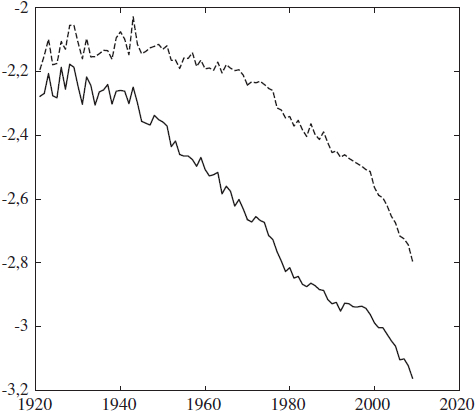
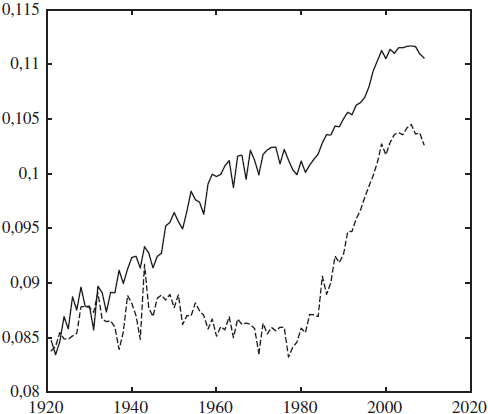



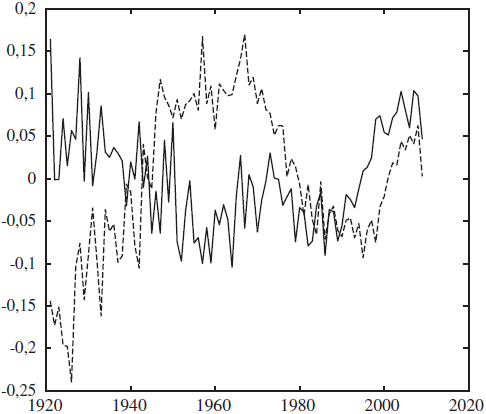

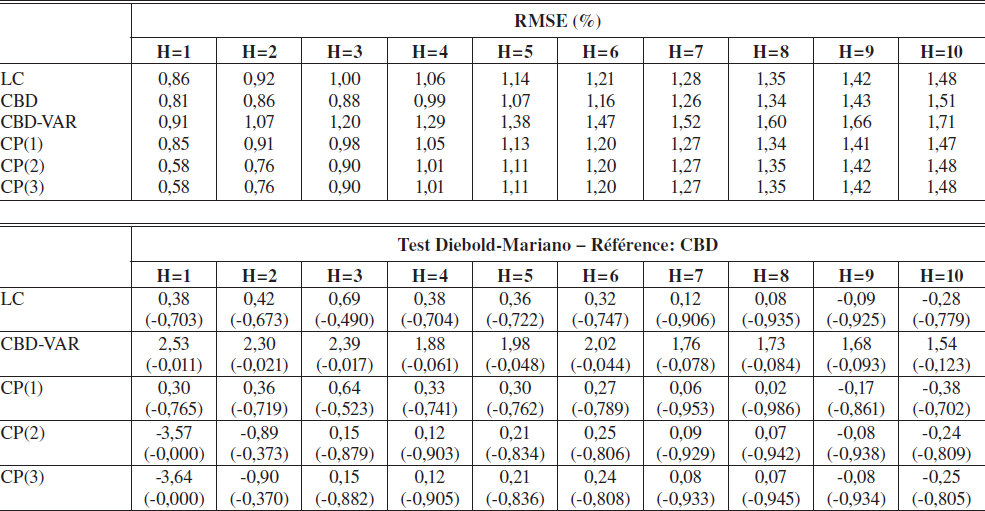


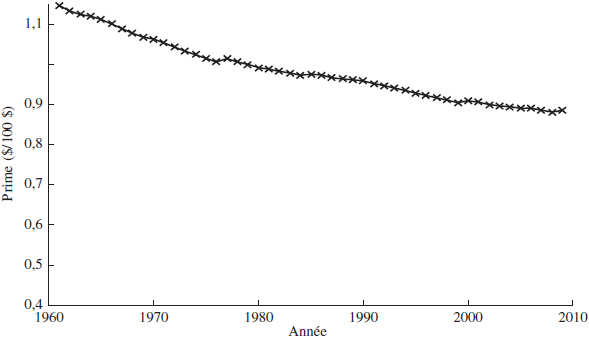

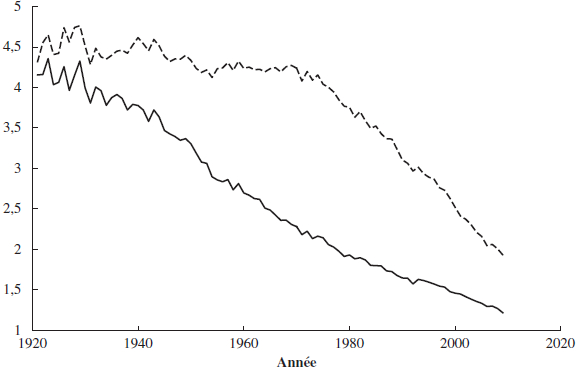



 , où
, où