Abstracts
Résumé
Dans le cadre de Bâle-2, l’étude vise à calculer pour les banques canadiennes la charge en capital afférente aux engagements de crédit hors bilan qui s’avère consistante avec celle des prêts au comptant au bilan. Cette consistance s’obtient en sélectionnant le risque de crédit des engagements (par similitude avec celui des prêts commerciaux) au lieu de la durée initiale des engagements (comme prescrit par Bâle-2) comme déterminant principal du calcul. Pour y arriver, nous proposons la « valeur de ou au modèle » comme approche avancée fondée sur les notations internes (NI) : dans celle-ci, le risque de crédit est appréhendé par une option de vente (put) basée sur une distribution de Johnson à quatre paramètres de la « valeur d’endettement à terme » (ce terme désignant la valeur de modèle de l’engagement). Ensuite, lors du calcul de la « juste » charge en capital d’un engagement, le risque « réel » de crédit, évalué comme put à terme de Johnson, est combiné avec la proportion de tirage de la ligne de crédit. Cette charge étant très modérée, l’approche « valeur de modèle » constitue une approche NI avancée « efficiente » puisqu’elle réduit la charge en capital par rapport à celle obtenue par l’approche Bâle-2 simplifiée ou même par rapport à celles obtenues par d’autres procédures NI avancées propres aux banques. Enfin, la valeur au modèle permet de déterminer la charge en capital additionnelle induite par une baisse de la cote de crédit d’un emprunteur. Cette application pratique s’appuie sur la correspondance entre valeurs d’endettement et cotes de crédit d’agences de notation externes ainsi que sur l’existence d’une matrice de probabilités de transition entre notations de crédit en début et fin de période.
Abstract
This research aims to bring some internal consistency to the computation of the credit-risk capital charge of loan commitments and commercial spot loans, namely the components of the commercial credit continuum. Consistency is achieved by using commitment credit risk (as for commercial-loan risk) instead of commitment initial term (as mandated by Basel-2) as the computation main determinant. This is done by proposing marking to model as the bank’s advanced internal-ratings-based (AIRB) approach : credit risk is captured by a four-parameter Johnson distribution of the commitment marked-to-model value (also known as the indebtedness futures value). Once priced as a Johnson’s futures put option, “true” credit risk is combined with the commitment exercise-cum-funding proportion so as to compute the commitment “fair” capital charge. As the latter is quite moderate, marking to model is an “efficient” AIRB approach that offers capital relief with respect to Basel-2 simplified approach but also with respect to the banks’ own alternative AIRB procedures. Marking to model also helps determine the banks’ incremental capital cost caused by borrowers’ credit-rating downgrades. This policy implication hinges on mapping indebtedness values into borrowers’ credit ratings of external agencies and using transition probabilities between beginning and end-of-period credit ratings.
Article body
Introduction
Selon Bâle-2[1], le ratio de capital s’obtient en divisant le capital réglementaire par l’actif pondéré pour le risque (l’APR). Par contre, Bâle-3 introduit de nouveaux ratios de capital et redéfinit sa composition, alors que Bâle-1 et Bâle-2 définissaient principalement les méthodes et paramètres utilisés pour calculer l’APR. La présente recherche examine le continuum du crédit commercial afin que l’APR des engagements de crédit hors bilan devienne consistant avec celui des prêts au comptant au bilan (spot loans). Actuellement, selon l’approche Bâle-2 simplifiée, l’échéance initiale des engagements détermine le facteur de risque de crédit, c.-à-d. le produit du facteur de conversion du crédit et du facteur principal du risque de crédit : pour les engagements irrévocables dont l’échéance est d’un an ou moins[2], le facteur de risque de crédit est de 20 %, alors qu’il est de 50 % pour les engagements dont la durée est de plus d’un an. Et tant pour les engagements courts que longs, Bâle-2 ne fait pas la distinction entre engagements au taux de base et hors taux de base, et, pour ces derniers, il ne tient pas non plus compte de leur note de crédit. Par opposition, les prêts commerciaux sont classifiés selon leur cote de crédit d’agences de notation externes, la durée initiale des prêts ne constituant qu’un facteur d’ajustement secondaire. Or, lors du tirage d’une ligne de crédit hors bilan, le montant tiré devient un prêt au bilan comme les autres prêts au comptant, avec les mêmes coefficients de calcul de l’APR que pour ces derniers. Aussi, semblerait-il raisonnable que le risque de crédit des engagements et des prêts soit évalué d’une manière consistante, même si celle-ci n’est pas en tout point similaire. En effet, une parfaite concordance n’est point souhaitable puisque certains aspects des engagements sont différents de ceux des prêts au comptant. De plus, afin que le risque de crédit devienne le facteur déterminant commun aux engagements et aux prêts, il nous faut d’abord démontrer qu’il constitue bien le principal facteur de risque des engagements hors bilan.
Les concepts analytiques que nous allons développer devant être ensuite corroborés par des résultats empiriques, il nous faut expliquer pourquoi nous nous concentrons sur les engagements de crédit, et plus précisément, sur ceux irrévocables à court terme. Il y a deux raisons à cela. La première est que les engagements de crédit constituent le plus important des instruments de crédit hors bilan. Pour étayer cette affirmation, nous examinons certains agrégats canadiens couvrant les six plus importantes banques à charte[3]. En 2010, le montant contractuel de tous leurs engagements irrévocables (362 milliards de $) représente 81,3 % des 445 milliards de l’ensemble de leurs instruments de crédit hors bilan. Le montant inutilisé des engagements représente également 96,5 % des 375,1 milliards de $ de prêts commerciaux portés au bilan. Quant aux 139,7 milliards de $ d’engagements irrévocables courts sur lesquels nous nous concentrerons, ils représentent 38,6 % du total des engagements irrévocables. En bref, les engagements de crédit sont essentiels à l’activité de crédit commercial des banques.
La seconde raison est que Bâle-2 modifie la façon dont est calculé l’APR des engagements irrévocables à court terme. Dans l’approche simplifiée, un facteur de conversion du crédit (FCC) de 20 % est tout d’abord appliqué au montant contractuel des engagements, puis à cet équivalent-crédit est appliqué un facteur de risque principal (FRP) de 100 %; sous Bâle-1, ces deux facteurs étaient nuls[4]. Au-delà de l’approche simplifiée, Bâle-2 offre aussi des approches de base et avancée fondées sur des notations internes (NI); par souci de clarté, nous nous concentrons sur l’approche avancée qui permet à certaines banques de déterminer elles-mêmes la façon de calculer leur charge en capital, pour autant que leur méthode de calcul soit acceptée par les régulateurs au vu du processus de supervision prévu au second pilier de Bâle-2[5]. Aussi, serons-nous guidés dans la recherche d’une approche NI avancée par trois critères : l’efficience de l’approche retenue, son acceptation par les régulateurs et sa cohérence interne avec les prêts au comptant. Par efficience, nous entendons que la procédure NI avancée vise à minimiser la charge en capital afférente au risque de crédit des engagements. Son acceptation par les régulateurs découle du fait que la procédure d’évaluation retenue est basée sur l’absence d’arbitrage, cette dernière étant déjà acceptée pour les nombreuses options sujettes aux règles de Bâle-2. Enfin, par cohérence du continuum du crédit commercial, nous entendons que la procédure NI avancée pour les engagements soit consistante avec celle utilisée pour les prêts au comptant.
Au vu de ces critères, nous nous proposons de remplacer les facteurs de conversion et de risque de l’approche Bâle-2 simplifiée par des concepts d’un modèle qui est non seulement considéré comme une approche NI avancée mais est aussi consistant avec les coefficients utilisés pour les prêts commerciaux au bilan, soit la probabilité de défaut (PD), l’exposition en cas de défaut (ECD), la perte en cas de défaut (PCD) et un ajustement de maturité (M). Par souci de clarté, nous faisons aussi abstraction des garanties et accords généraux de compensation (netting), tant pour les engagements que pour les prêts au comptant. Aussi, proposons-nous l’approche de valeur déterminée par modèle (marking-to-model) dans laquelle la charge en capital des engagements est basée sur la « valeur de modèle »[6] de la ligne de crédit (valeur à laquelle nous ferons référence à partir d’ici sous le vocable de valeur d’endettement). Cette dernière comprend une mesure implicite du risque « réel » de crédit des engagements, laquelle sera combinée ensuite avec le montant moyen du tirage lorsque l’engagement est exercé. Enfin, nous compléterons la valeur de modèle en introduisant une correspondance isomorphe entre valeurs d’endettement et cote de crédit d’agences de notation externes. Dès lors, la valeur de modèle du risque de crédit des engagements sera considérée comme une approche NI avancée présentant les propriétés suivantes : (i) elle combine la valeur de l’option de vente (ci-après le put), qui capte le risque de crédit de l’engagement, avec une proportion empirique du tirage de l’engagement, (ii) elle substitue valeur du put et proportion de tirage aux facteurs de conversion et de risque prescrits par l’approche Bâle-2 simplifiée, (iii) elle est acceptée par les régulateurs puisque la valeur du put d’engagement est basée sur l’absence d’arbitrage, et enfin, (iv) ses nouveaux coefficients sont consistants avec ceux des prêts au comptant (soit PD, ECD, PCD et M). L’approche « valeur au modèle » soulève au moins trois questions. Le put européen généré par Bâle-2 reflète-t-il effectivement le risque « réel » de crédit des engagements? Ensuite celui-ci capte-t-il bien les phénomènes d’asymétrie et d’aplatissement présents dans la distribution de probabilité des accroissements proportionnels de la valeur d’endettement? Finalement la « juste » charge en capital calculée à partir de la « valeur au modèle » constitue-t-elle une approche NI avancée « efficiente » par rapport à la procédure Bâle-2 simplifiée, voire même par rapport à d’autres procédures NI avancées propres aux banques?
Depuis l’introduction de la valeur d’endettement par Thakor et al. (1981), l’évaluation du risque de crédit par un put d’engagement se fait généralement dans le cadre de modèles structurels. Par exemple, Thakor et al. (1981) et Ho et Saunders (1983) dérivent la valeur du put implicite aux engagements à taux fixe, Thakor (1982) et Chateau et Dufresne (2002) obtiennent des formules de puts européen et américain respectivement pour les engagements à taux variable, et Chateau et Wu (2007) déterminent la valeur du put implicite aux engagements extensibles. Hawkins (1982) enfin détermine la valeur des lignes renouvelables (revolving lines) alors que Loukoinova et al. (2007) modélisent les engagements de crédits garantissant le papier commercial. Récemment toutefois, Jarrow et al. (1997), Hugston et Turnbull (2001) ainsi que Chava et Jarrow (2007) ont mis de l’avant une approche indirecte (forme réduite) qui assimile l’évaluation du risque des engagements à celle du risque de crédit d’obligations sujettes à défaut (Jarrow et Turnbull, 1995). Cette approche a le mérite d’évaluer simultanément les aspects au et hors bilan des lignes de crédit. Mais de ce fait même, elle ne tient pas compte, lors du calcul de la charge en capital, que les pondérations prescrites par Bâle-2 pour le risque de crédit des engagements sont différentes de celles prescrites pour celui des obligations corporatives. L’approche indirecte est aussi problématique pour les principaux utilisateurs des engagements, les firmes petites et moyennes, qui n’ont souvent pas accès au marché obligataire. Les engagements constituent un marché primaire sans marché secondaire : or, c’est à partir du marché obligataire secondaire que l’approche indirecte obtient le prix des obligations et l’information spécifique aux firmes. En dernier lieu, l’évaluation indirecte est très tributaire de la calibration des paramètres de la structure par terme des taux d’intérêt, une problématique mise en évidence, entre autres, par Nawalka et al. (2007) et Pennacchi (2008). Quant à nous, nous proposons une approche structurelle étendue qui intègre les facettes suivantes : (i) la valeur du put à terme implicite à tout engagement reflète correctement son risque « réel » de crédit, (ii) cette valeur incorpore bien dissymétrie mais surtout excès d’aplatissement positif de la distribution des variations de la valeur d’endettement à terme[7] et (iii) le put de Johnson constitue une avancée par rapport à celui de Gram-Charlier sous contraintes utilisé, précédemment, entre autres, par Corrado (2007), Chateau (2009), ou encore Jurczenko et al. (2004). Notre expression finale constitue dès lors la valeur du put à terme implicite à tout engagement irrévocable court.
Dans la mesure où la valeur du put reflète correctement le risque de crédit des engagements, il semble raisonnable de déterminer son impact sur la charge en capital prescrite par Bâle-2 pour cet instrument financier. Dans le rapport annuel de la banque, la valeur agrégée des engagements courts inutilisés est portée hors bilan lors de la présentation du bilan consolidé. La date du rapport annuel coïncide aussi souvent avec celle de l’audit de suffisance de capital de Bâle-2. Or, à cette date, pour de nombreux engagements d’échéance initiale à un an, la durée restante à courir jusqu’à l’échéance de l’exposition au risque de crédit est inférieure à un an. Bien que ce soit la marge fixe d’un engagement à taux variable[8] qui donne naissance au put, c’est la date d’audit fixe de Bâle-2 qui confère à celui-ci son caractère européen. Dès lors, la valeur du put à terme européen constitue pour la banque un passif notionnel dû à ce qu’elle détient un montant d’engagements inutilisés lors de l’audit de la suffisance de capital.
Les développements de l’approche « valeur de modèle » du risque de crédit des engagements comprennent trois étapes. Lors d’une première étape analytique, nous définissons la valeur d’endettement à terme et la proportion de tirage; cette dernière combine une fonction indicatrice (d’exercer ou non l’engagement) à la proportion de tirage qui elle croît avec le temps restant jusqu’à l’échéance de l’engagement. Pour les montants des engagements inutilisés à la date d’audit, nous évaluons la valeur des puts générés par Bâle-2, soit le put à terme de Johnson pour la valeur au modèle et ceux de Gram-Charlier et Black (1976) pour deux procédures NI avancées alternatives propres aux banques. Ces divers puts sont combinés ensuite avec la proportion de tirage pour calculer l’APR des engagements et, finalement, la charge en capital correspondant à leur risque de crédit. Les puts implicites aux engagements ne constituant que des valeurs notionnelles, nous avons recours, dans une deuxième étape empirique, à des simulations qui permettent d’évaluer le coût de l’exposition des banques au risque de crédit des engagements. Lors de l’estimation par simulation, nous examinons deux caractéristiques des puts. La première indique que la composante risque du put est systématiquement plus importante que sa composante temps. Quant à la seconde, elle montre que les estimations des puts de Black et Gram-Charlier sont significativement plus élevées que celles du put de Johnson.
Finalement, la troisième étape traite de deux implications pratiques de l’analyse. Après des préliminaires qui positionnent la valeur au modèle dans le cadre des procédures simplifiée et NI avancée de Bâle-2, la première implication vise le calcul de la « juste » charge en capital afférente au risque « réel » de crédit des engagements irrévocables courts. L’approche valeur au modèle du risque de crédit des engagements produit une charge en capital modérée et aligne les exigences en capital réglementaire des engagements avec celles des autres prêts au bilan. En considérant ensuite la « juste » charge en capital de l’approche valeur au modèle comme étalon de mesure, nous démontrons que celle-ci est inférieure non seulement à celle de la procédure Bâle-2 simplifiée mais aussi à celles de procédures NI avancées alternatives basées sur les puts de Black et Gram-Charlier. Finalement, la seconde implication pratique constitue une application intéressante de l’approche « valeur de modèle » : comment les banques déterminent-elles l’accroissement de charge en capital induit par une baisse de la note de crédit de leurs emprunteurs?
L’article est organisé de la façon suivante. La première section définit la valeur d’endettement des engagements et détermine la valeur des puts européens à terme de Black, Gram-Charlier et Johnson implicites aux engagements irrévocables courts; elle détermine aussi la proportion de tirage des engagements. Les estimations des simulations sont présentées à la deuxième section et utilisées dans la troisième section pour étayer les implications pratiques. De brèves conclusions sont présentées dans la dernière section.
1. Évaluation des engagements irrévocables à court terme
1.1 Les engagements irrévocables courts dans le cadre réglementaire de Bâle-2
Dans le diagramme décisionnel, nous ne retenons que les caractéristiques strictement nécessaires à l’analyse d’un engagement présentant une marge à terme fixe. Le diagramme vise un engagement à court terme, mais demeure aussi valable pour un engagement à plus long terme (seuls changent le terme de l’engagement et la durée du prêt). À l’étape 1 et en S1, la banque offre à la date 0 un engagement irrévocable court présentant les caractéristiques suivantes : (i) la période d’engagement, [0, T], est d’une année, (ii) la durée du prêt, [T, T*], est d’un an à partir de T si la ligne de crédit est tirée (nous expliquons plus tard dans cette sous-section comment la date d’audit fixe confère au put son caractère européen), (iii) la valeur maximale de la ligne est fixée à L = 100 $, et (iv) le taux de base variable comprend deux composantes additives. La première, cT, le coût du financement stochastique payable à la date T, est supporté par l’emprunteur, le taux sur acceptations bancaires (AB) étant souvent utilisé comme indice exogène[9]. La seconde, la marge à terme fixe, m̅0 est fixée par la banque lors de la création de l’engagement à la date 0. Pour faciliter les références ultérieures, l’engagement d’un maximum de 100 $ est créé le 1er juillet (date 0), vient à échéance le 30 juin (date T) et a une marge à terme fixe de 2 % par an[10]. Qui dit engagements irrévocables dit contrats non résiliables en ce qui concerne leur évaluation par absence d’arbitrage. C’est sans doute la raison pour laquelle Bâle-2 a introduit de nouveaux coefficients (FCC de 20 % et FRP de 100 %) pour ces engagements irrévocables courts. Bien que les engagements inutilisés au taux de base ne présentent presque pas de défaut de paiement, le risque minime de défaut potentiel pour ceux déjà exercés (ils deviennent alors des prêts au bilan susceptibles de défaut de paiement) justifie une marge à terme positive. De plus, leur probabilité de défaut est encore réduite par une clause standard de « changement adverse significatif » (material-adverse-change clause) qui les rend résiliables au gré de la banque[11]. Enfin, notons que Bâle-2 traite différemment des corrélations du continuum de crédit commercial : il ne tient pas compte des corrélations entre engagements hors bilan mais bien de celles du portefeuille de prêts commerciaux au bilan.
Afin d’intégrer l’engagement dans le cadre réglementaire de Bâle-2, nous introduisons maintenant deux dates : l’âge de l’engagement et la date fixe de l’audit de suffisance de capital de Bâle-2. Dans la partie S1 du diagramme, la première date j (avec t = 0 ≤ j ≤ T = 12 mois) définit deux périodes : T – j, la durée restante de l’engagement initial d’une année et j – t, l’âge de l’engagement. Par exemple, si j = 5 mois, l’engagement d’un an est maintenant âgé de cinq mois (j – t = 5) et il reste 7 mois à courir jusqu’à son échéance (T – j = 7). En S2, la seconde date s est celle de l’audit fixe qui coïncide ici avec j par souci de clarté. Dès lors, l’engagement (âgé) de j mois est évalué à la date d’audit fixe s et la durée à courir jusqu’à son échéance est inférieure à la période initiale d’un an. Au vu de notre engagement de juillet à juin, la date d’audit fixe de Bâle-2 coïncide avec celle de la fin de l’année fiscale de la banque, le 31 décembre. La date d’audit j = s fonctionne dés lors comme la date 0 d’évaluation du put européen (cf. la sous-section 1.3 concernant le put implicite à l’engagement). Enfin, la décision d’exercer ou non l’engagement ainsi que celle de la proportion du tirage de la ligne de crédit de la date s jusqu’à la date T sont formalisées à la sous-section 1.5.
1.2 Brève analyse des données chronologiques
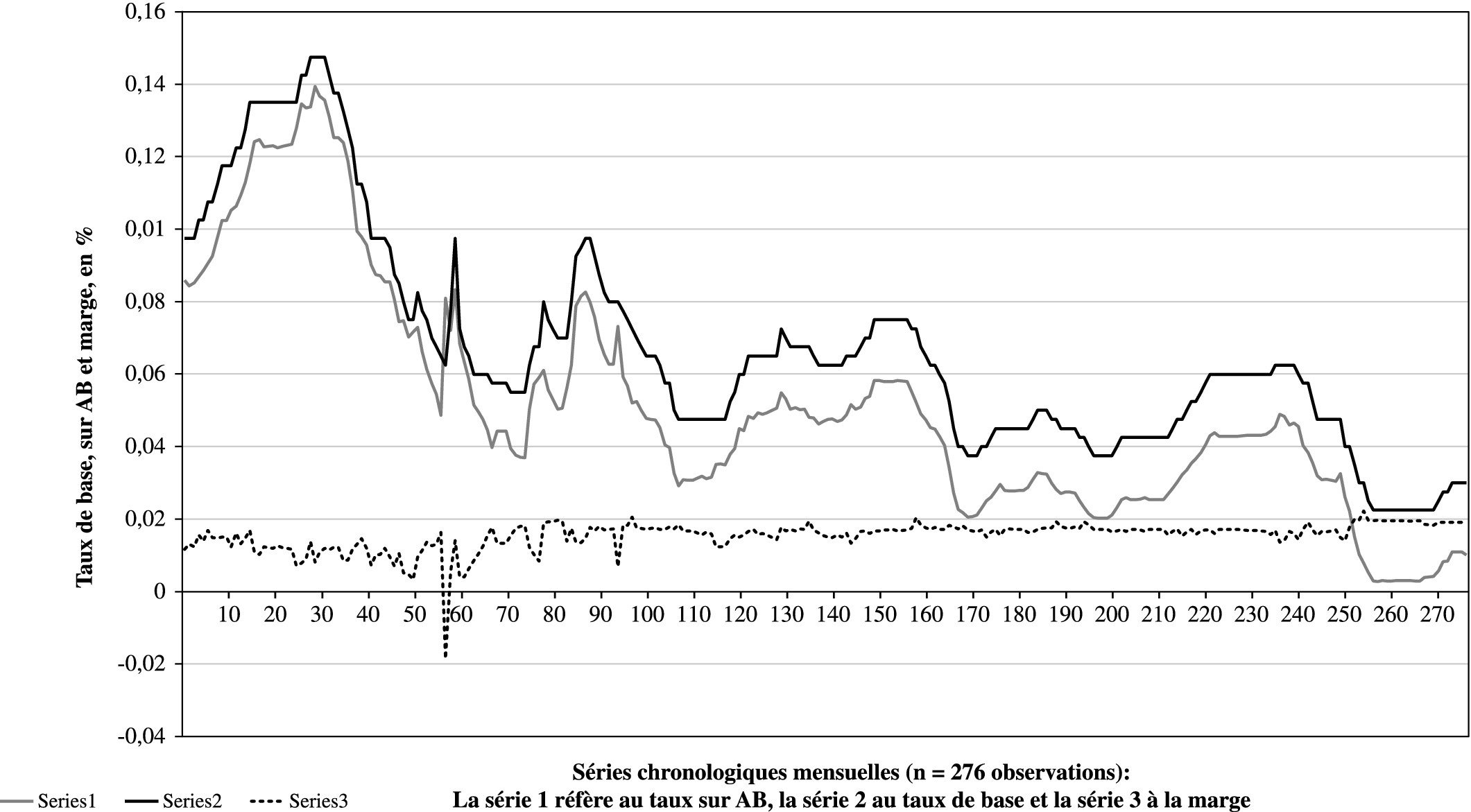
Le taux de base variable canadien comprend deux composantes : le taux sur les acceptations bancaires (AB) plus une marge. Les séries chronologiques du taux de base, du taux sur AB et de la marge comprennent 276 observations mensuelles de janvier 1988 à décembre 2010 (janvier 1988 coïncidant avec l’introduction de la réglementation de Bâle-1). L’inspection des séries temporelles du graphique 1 révèle certaines caractéristiques intéressantes. Pour les engagements à taux variable, l’évolution des taux de base et sur AB est très similaire (témoin leur corrélation ρ = 0,994 presque parfaite). Par contre, l’autre composante du taux de base, la marge, demeure relativement stable au cours du temps mais évolue différemment des taux de base et sur AB (par exemple, la corrélation entre marge et taux sur AB est de -0,578). Actuellement, la marge moyenne évolue autour de deux pour cent par année. Les variations mensuelles des séries révèlent aussi certaines tendances intéressantes (qui ne font pas l’objet d’un graphique séparé par souci de parcimonie) : l’amplitude des baisses mensuelles dans le taux sur acceptations est généralement plus grande que celle des baisses dans le taux de base, alors que les hausses mensuelles du taux sur acceptations sont plus petites que celles du taux de base. De plus, les variations mensuelles des acceptations ont lieu un mois avant celles dans le taux de base. En d’autres termes, la marge ne constitue qu’une variable d’ajustement qui absorbe les variations mensuelles avant de retourner progressivement vers sa valeur moyenne.
Graphique 1
Taux de base, taux sur acceptations bancaires (AB) et marge de crédit, Canada, de 1988.01 à 2010.12
1.3 Le put à terme européen implicite aux engagements irrévocables courts et l’évidence statistique afférente aux variations de la valeur d’endettement
Commençons par définir la valeur d’endettement, F. Selon l’approche d’absence d’arbitrage, la valeur d’endettement à terme à la date 0, F0, est égale à la valeur nominale de la ligne de crédit, L, car la marge à terme fixe m̅0 est égale à la marge stochastique sur prêt au comptant, m0 = l0 – c0, cette dernière étant définie comme la différence entre l0, le taux de crédit de base, et c0, le taux de financement sur le marché des acceptations bancaires. Étant donné les marges à terme fixe et au comptant variable, nous définissons alors la valeur d’un endettement à terme (âgé) de j mois, Fj. Soit :
où (m̅0 – mj) définit la différence entre la marge à terme à la date 0 et la marge au comptant à la date j, (T* – T) la durée du prêt (un an) à partir du moment où l’engagement est exercé, et L la valeur nominale constante de la ligne de crédit. Pour un engagement d’échéance initiale d’un an par exemple, F5 définit une valeur d’endettement (âgée) de cinq mois dont la durée à courir jusqu’à son échéance est de sept mois. Supposons maintenant qu’à la date j = s de l’audit de Bâle-2 (le 31 décembre), les fluctuations du taux de base variable sur les prêts au comptant entraînent l’inégalité suivante : m̅0 < mj. Selon l’équation 1, le détenteur de l’engagement décide alors de tirer sur la ligne de crédit car la marge à terme fixe est inférieure à celle au comptant stochastique. Par exemple, si la marge à terme de 2 % de la sous-section 1.1 est combinée avec une marge au comptant, disons, de 3 %, l’équation 1 donne naissance à un put à terme implicite, puisque la valeur d’endettement, Fj, est inférieure au prix d’exercice, L. En d’autres termes, les fluctuations de la marge au comptant à la date fixe j = s d’audit de Bâle-2 donnent naissance à une valeur d’endettement de cinq mois ainsi qu’à un put européen à terme de sept mois généré par un engagement initial d’un an.
Au vu de l’équation 1, nous considérons maintenant la distribution des variations mensuelles proportionnelles de la valeur d’endettement. Soit
où tF(j) désigne la valeur à la date t d’une valeur d’endettement (âgée) de j mois. L’expression (2) génère dès lors une série chronologique de changements mensuels proportionnels de la valeur d’endettement à terme qui, elle, demeure continuellement de j mois. Dans le document 1, nous présentons les variations proportionnelles de Fj du troisième au neuvième mois. Au vu de l’évidence statistique présentée dans la deuxième colonne, la moyenne des variations proportionnelles de la valeur d’endettement est proche de 0 % pour toutes les valeurs d’endettement, ce qui corrobore notre hypothèse que Fj est effectivement une valeur à terme. Nous inférons également des valeurs rapportées dans les colonnes 6 à 8, qu’au cours de ces 23 années, la plupart des valeurs d’endettement varient dans l’intervalle de 96,2 $ à 104,1 $. Dans la troisième colonne, la volatilité des distributions empiriques fluctue peu dans l’intervalle étroit de [1,58 % par an à 1,69 % par an] pour les variations du log de F calculées pour les mois considérés. Les intervalles de confiance pour les coefficients d’asymétrie et d’aplatissement pour un échantillon normal comprenant 276 observations sont calculés dans la note au bas du document 1. Selon les estimés présentés dans les colonnes quatre et cinq, plusieurs coefficients d’asymétrie positifs et négatifs ainsi que tous les coefficients d’aplatissement se trouvent hors de leurs intervalles de confiance respectifs. Ceci indique que les distributions empiriques présentent principalement une faible asymétrie couplée à une forte tendance leptocurtique (excès d’aplatissement positif). Les estimations historiques du document 1 ne constituent que des approximations des coefficients de volatilité, d’asymétrie et d’aplatissement qui seront utilisées à la section 2 lors de l’estimation du put implicite aux engagements de crédit.
Document 1
Analyse statistique des 276 observations mensuelles de la série chronologique des pourcentages de variations de la valeur d’endettement calculés à partir de l’équation 2 pour la période 1988.01 à 2010.12
Pour un échantillon de taille n = 276 observations, l’intervalle de confiance à 95 % des coefficients de Pearson d’asymétrie β1 et d’aplatissement β2 d’un échantillon de la distribution normale sont : ± 1,96(6/276)½ = ± 0,289 et 3 ± 1,96 (24/276)½ = 3 ± 0,578, respectivement.
Valeur mensuelle non biaisée (divisée par n – 1) × √12 = σ en pourcentage par année.
d.a. indique le nombre de données aberrantes ou de valeurs extrêmes (outliers).
1.4 Le put à terme européen à quatre moments implicite aux engagements de crédit
Selon Bâle-2, au-delà de l’approche simplifiée basée sur des facteurs comptables donnés, les banques peuvent proposer leur propre procédure NI avancée. La plus simple consiste à appréhender le risque de crédit des engagements à l’aide du put à terme européen de Black (1976), un choix qui ne peut qu’être approuvé par les régulateurs puisque les options de Black-Scholes sont utilisées pour d’autres instruments sujets à la réglementation de Bâle-2. Plus spécifiquement, ce put européen à terme PB s’écrit :
avec
où d1 désigne le
seuil (avec ![]() ) de N(.), la distribution
normale standard, r le taux d’intérêt
sans risque à court terme, σ l’écart type de la valeur d’endettement à
terme et T la date d’échéance du
put, les autres termes ayant été
déjà définis précédemment. Se pose alors la question de comment améliorer le
put à deux moments de Black par un
modèle qui tienne compte simultanément des coefficients de volatilité,
d’asymétrie et d’aplatissement du document 1?
) de N(.), la distribution
normale standard, r le taux d’intérêt
sans risque à court terme, σ l’écart type de la valeur d’endettement à
terme et T la date d’échéance du
put, les autres termes ayant été
déjà définis précédemment. Se pose alors la question de comment améliorer le
put à deux moments de Black par un
modèle qui tienne compte simultanément des coefficients de volatilité,
d’asymétrie et d’aplatissement du document 1?
L’approche la plus couramment utilisée pour évaluer les options comprenant quatre moments est celle de Gram-Charlier proposée par Corrado et Su (1996), cette dernière étant aussi utilisée par d’autres auteurs, parmi lesquels, Bakshi et Madan (2000), Jurczenko et al. (2004) ou Corrado (2007). L’expansion de type A de Gram-Charlier des variations proportionnelles de la valeur d’endettement ne constitue toutefois une vraie densité de probabilité que si cette dernière satisfait la contrainte de Jondeau-Rockinger (2001) sur les coefficients d’asymétrie et d’aplatissement. Numériquement, ceci implique que ces derniers se trouvent dans l’ellipse admissible définie par les valeurs des coefficients d’asymétrie et d’aplatissement, soit les intervalles [-1,0493, 1,0493] et [3, 7] respectivement, ce afin d’éviter qu’il y ait des probabilités négatives dans les queues de la distribution. La distribution de Gram-Charlier est introduite ensuite dans la condition de rémunération terminale (payoff) de l’option qui est développée jusqu’à l’obtention de la forme analytique du put européen à terme comprenant quatre moments. Pour les engagements de ligne de crédit, la dérivation de la valeur du put de Gram-Charlier sous les contraintes de martingale et de Jondeau-Rockinger est présentée chez Chateau (2009). Soit :
où
avec
et
De plus, μ3 et μ4 désignent les moments centrés d’ordre i, pour i = [3, 4], ω tient compte de ces moments dans d1 (notez la différence avec d1 dans l’équation 3) et
et
où F*0 ≡ F0(1 + ω)-1 et n(d1) désigne la densité de probabilité normale standardisée de d1. Plus concrètement, le put d’engagement de Gram-Charlier PGC de l’équation 4 comprend le put d’engagement à terme de Black PB, plus deux termes d’ajustement afférents à l’asymétrie et à l’excès d’aplatissement positif, respectivement. Les banques peuvent alors utiliser le put de Gram-Charlier pour proposer une deuxième approche NI avancée plus sophistiquée que celle basée sur l’équation 3.
Toutefois, l’examen du document 1 révèle que, si les valeurs du coefficient d’asymétrie se trouvent bien dans l’intervalle de Jondeau-Rockinger, ce n’est clairement pas le cas pour celles du coefficient d’aplatissement, qui elles varient entre 22,28 et 36,24[12]. Il nous faut dés lors trouver une autre distribution qui tienne compte des valeurs d’aplatissement du document 1 supérieures à sept, la borne supérieure de la contrainte de la distribution de Gram-Charlier. La réponse affirmative se trouve dans une famille de courbes de fréquence basée sur le système de « translation » de Johnson (1949) où la variable transformée z = h(x) est considérée comme ayant une distribution normale. Cette transformation basée sur quatre paramètres est introduite ensuite dans la condition de rémunération terminale de l’option que nous développons jusqu’à l’obtention de la formule analytique du put européen à terme. Ces développements sont présentés dans l’annexe et l’expression finale PJ est appelée la valeur du put à terme européen de Johnson. Soit :
où γ, δ, ξ et λ désignent les quatre paramètres du système non borné SU défini dans l’annexe, Q = γ + δ sinh-1 [(L – ξ)/λ] où sinh-1 désigne l’inverse de la fonction sinus hyperbolique, les autres termes ayant été déjà définis précédemment. L’avantage du put de Johnson est qu’il tient compte des valeurs fortement leptocurtiques du coefficient d’aplatissement du document 1, versus une valeur maximale de 7 pour le put de Gram-Charlier sous contrainte. En d’autres termes, la méthode d’ajustement par les moments constitue une extension de l’approche de Gram-Charlier sous contrainte; extension qui se traduit par des différences significatives dans les valeurs des puts présentées dans le tableau 1 ci-après. Aussi, proposons-nous que l’évaluation au modèle, dans laquelle le put de Johnson capte le risque de crédit des engagements, soit considérée comme une procédure NI avancée.
1.5 Exercice de l’engagement et exposition en cas de tirage (ECT)
Une fois le put de Johnson évalué, la détermination de la proportion de la ligne de crédit qui sera tirée à partir de la date j = s jusqu’à T se fait en deux étapes : (i) l’exercice de l’engagement est appréhendé par l’indicateur 1condition, qui est égal à 1 si la condition se vérifie et à 0 autrement, et (ii) il est combiné avec dj, la proportion de tirage de lignes de crédit âgées de j mois. La proportion moyenne conditionnelle à la date j pour la période T – j, désignée par 0 ≤ πT – j ≤ 1, est :
et sa proportion complémentaire est
Étant donné qu’au niveau de la banque, l’audit de Bâle-2 s’applique à l’agrégat des engagements irrévocables courts, nous proposons la solution de calcul suivante :
la proportion moyenne de tirage est une fonction croissante de la durée à courir jusqu’à l’échéance de l’engagement, et
l’engagement de 100 $ fonctionne comme unité de référence qui est soit tirée complètement soit pas du tout, tout tirage partiel étant réalloué à ces deux proportions.
En pratique, le montant total du tirage des engagements (âgés) de j mois s’obtient en multipliant la proportion moyenne πT – j par le montant agrégé des engagements inutilisés à la fin du mois j. Nous appelons ce montant l’exposition en cas de tirage (ECT) à la date d’audit, et, lorsqu’il y a effectivement tirage, le montant tiré se transforme alors en prêt au bilan qui devient, selon Bâle-2, une exposition en cas de défaut (ECD) à laquelle est attachée une probabilité de défaut (PD). Quant à (1 – πT – j), appliqué au montant agrégé du même mois, il détermine pour la banque le montant total inutilisé des engagements, soit le total des portions inutilisées d’engagements exercés partiellement et des montants des engagements totalement inutilisés.
L’évidence empirique concernant exercice et tirage est parcellaire et incomplète. Morgan (1993) indique que la fraction du montant maximum de l’engagement qui est réellement tirée par les emprunteurs au taux de base variable est de 55 % entre 1988 et 1990; malheureusement, il ne donne pas le nombre des engagements qui demeurent totalement inutilisés. Martin et Santomero (1997) rapportent que les firmes ne tirent typiquement que 65 % du maximum de la ligne de crédit. Par contre, Sufi (2009) rapporte que seulement 38 % des lignes de crédits sont utilisés par les 4011 firmes américaines publiques de son échantillon couvrant la période de 1996 à 2003. Enfin, dans l’étude de Jimenez et al. (2009) concernant les firmes espagnoles pour la période de 1984 à 2005, la proportion de tirage des lignes de crédit, qui ne sont pas en défaut, est de 47 %[13]. Ils indiquent aussi que 16 % des lignes demeurent inutilisés, que 6 % sont utilisés en totalité et que la distribution du tirage des autres autour de 47 % est relativement symétrique. Au vu de cette évidence, nous choisissons une proportion de tirage πT – j qui varie avec la durée restante jusqu’à l’échéance de l’engagement. Par exemple, une proportion πT – j ≡ π3m = 45 % indique que, pour les engagements irrévocables courts pour lesquels il ne reste que trois mois jusqu’à leur échéance, 45 % du montant total inutilisé est tiré; cette proportion monte à π9m = 75 % pour les engagements pour lesquels il reste neuf mois jusqu’à leur échéance, étant donné que les emprunteurs ont plus de temps et d’opportunités pour procéder aux tirages. À ce stade, nous possédons maintenant tous les éléments pour passer à l’estimation du risque de crédit des engagements.
2. Estimation par simulations
2.1 Paramètres de la simulation et signification des estimations
Les valeurs d’endettement n’étant point transigées sur un marché, les estimations de leur put implicite ne constituent que le coût notionnel de l’exposition de la banque au risque de crédit d’engagements irrévocables courts. Pour calculer ces passifs notionnels, nous utilisons l’évidence statistique présentée dans le document 1 de la sous-section 1.3. La plupart des valeurs d’endettement à terme du document 1 variant entre 96,2 $ et 104,1 $, nous fixons les valeurs de Fj à 100 $, 99,5 $, 99 $, 98,5 $, 98 $ et 97,5 $ pour un put d’engagement qui devient progressivement en jeu (in the money)[14] puisque la valeur d’exercice est de L = 100 $. Pour ces valeurs d’endettement, les simulations sont basées sur un taux d’intérêt court sans risque r de 3 %, une durée à courir jusqu’à l’échéance (T – j) de 3 à 9 mois ainsi que sur les valeurs de volatilité et d’asymétrie du document 1. Concernant le coefficient d’aplatissement, nous choisissons pour le put de Gram-Charlier la valeur 6,5, juste inférieure à la limite supérieure définie par Jondeau-Rockinger. Pour le put de Johnson, nous utilisons la procédure itérative d’Elderton-Johnson (1969) qui accommode les valeurs plus élevées du coefficient d’aplatissement du document 1. Il existe aussi une bonne raison pour préférer une simulation à un test sur le passé (back-testing). Depuis 1988, les règles de Bâle ont été modifiées constamment, permettant aux banques de pratiquer, pour les engagements, les arbitrages réglementaires suivants : sous Bâle-1, elles accroissaient leurs engagements courts au détriment des engagements longs puisque les facteurs de conversion et de risque étaient inférieurs pour les premiers. Même actuellement sous Bâle-2, les banques continuent à substituer des engagements révocables courts à ceux irrévocables courts étant donné que les facteurs de conversion et de risque des premiers sont encore nuls. Dans de telles circonstances, un test rétrospectif ne présente qu’un intérêt limité.
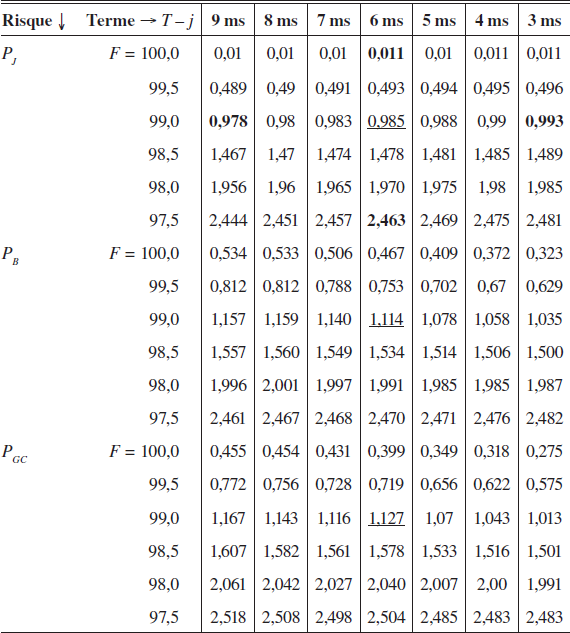
Avant d’analyser les résultats des simulations, nous clarifions la signification des estimations des puts à terme européens pour ce qui constitue notre scénario de référence, soit les coordonnées F = 99 $ et T – j = 6 mois, dans la première matrice du tableau 1. Cette estimation correspond à un put dont la valeur d’endettement F = 99 $ est légèrement en jeu et dont la durée à courir jusqu’à son échéance est de 6 mois. Selon l’estimation (soulignée) PJ = 0,985 $, le put de Johnson a une valeur d’équilibre légèrement inférieure à 1 % des 100 $ de l’engagement si la marge fixe à terme est de 2 % par an, lorsque simultanément la marge stochastique au comptant est de 3 % par an. Par contre, les valeurs correspondantes des puts à terme de Black et de Gram-Charlier, PB = 1,114 $ et PGC = 1,127 $ dans les deuxième et troisième matrices du tableau sont significativement plus grandes : ceci implique qu’elles sont surévaluées en termes de PJ.
2.2 Évaluation du risque de crédit en termes du put de Johnson
Deux tendances significatives se dégagent des matrices du tableau 1. La première concerne la valeur du put lui-même, qui reflète le coût encouru par la banque qui porte hors bilan à la date fixe d’audit de Bâle-2 des lignes de crédit inutilisées dont la durée jusqu’à expiration est variable. La matrice PJ du tableau 1 présente les sensibilités à la durée et au risque du put de Johnson : les variations de la durée restante jusqu’à l’échéance sont représentées par les lignes et celles au risque (c.-à-d. à la valeur d’endettement) par les colonnes. Dans ce dernier cas, pour la quatrième colonne de la matrice PJ pour laquelle T – j = 6 mois, les valeurs croissent fortement de 0,011 $ pour la valeur d’endettement au pair (F = 100 $) à 2,463 $ pour celle qui est la plus en jeu (F = 97,5 $) – ces deux valeurs étant en caractères gras dans le tableau 1. Une croissance exponentielle similaire est observée pour les engagements dont les termes jusqu’à l’échéance sont différents. Examinons ensuite les lignes de la matrice qui captent la sensibilité au terme du put. Sur la troisième ligne de la matrice PJ caractérisée par une valeur d’endettement de 99 $, les estimations du put de Johnson croissent à peine de 0,978 $ à 0,993 $ pour des durées à courir jusqu’à l’échéance qui décroissent de 9 à 3 mois. Les autres lignes présentent cette même croissance très légère. En d’autres termes, la matrice PJ indique clairement que les coûts du risque de crédit des engagements irrévocables courts sont beaucoup plus sensibles aux variations de risque qu’à celles de terme. Les commentaires concernant les valeurs des puts de Black et Gram-Charlier des deuxième et troisième matrices seront brefs. Les valeurs correspondantes de Black et Gram-Charlier sont généralement supérieures à celles du put de Johnson et, pour chaque ligne, elles ont généralement tendance à décroître lorsque la durée décroît de 9 à 3 mois, alors que c’est l’inverse pour celles du put de Johnson. Notons toutefois qu’il y a, pour les lignes de la matrice PGC dont les valeurs déclinent avec le temps restant jusqu’à l’échéance, une bosse ou un léger accroissement au terme de 6 mois pour les valeurs d’endettement de 99 $ et moins.
Tableau 1
Valeurs des puts de Johnson, Black et Gram-Charlier implicites aux engagements de crédit irrévocables à court terme
Matrice Pj : les valeurs du put européen à terme de Johnson de l’équation 8.
Matrice PB : les valeurs du put européen à terme de Black de l’équation 3.
Matrice PGC : les valeurs du put à terme de Gram-Charlier de l’équation 4.
Définition des paramètres : F = valeur d’endettement à terme en $ calculée à partir de l’équation 1; L = 100 $, la valeur d’exercice de la ligne de crédit en $; r = le taux d’intérêt à court terme sans risque exprimé en % par année; T = date d’échéance de l’engagement; et T – j = durée à courir jusqu’à l’échéance du put, en mois.
Note : Paramètres communs : L = 100 $; r = 3 % par an; T – j = 3,..,9 mois, avec T = 12 mois.
Les valeurs des paramètres de volatilité, d’asymétrie et d’aplatissement sont celles des colonnes 3 à 5 du document 1.
L’autre tendance reflète les différences entre les valeurs des cellules correspondantes des matrices (elles ne font pas l’objet d’un tableau séparé par souci de parcimonie) : celles-ci mettent en évidence l’impact des coefficients d’asymétrie et d’aplatissement sur le coût du risque de crédit des engagements. Cet impact est mesuré par les différences entre valeurs des puts des matrices de Black et Gram-Charlier et celles correspondantes de la matrice de Johnson, ces dernières étant choisies comme étalons de mesure. D’une façon générale, les valeurs des puts des matrices de Black et Gram-Charlier surestiment les valeurs correspondantes de la matrice de Johnson. Cette surestimation est très significative pour les valeurs d’endettement au pair ou faiblement en jeu, alors qu’elle demeure minimale pour les valeurs plus en jeu (98 $ ou moins). Par contre, la sur- ou sous-évaluation des valeurs de PB par rapport à celles de PGC est relativement mineure et non symétrique : pour les valeurs faiblement en jeu, la surévaluation des valeurs du put de Black peut atteindre 17,6 % alors que sa sous-évaluation pour les valeurs en jeu (98,5 $ ou moins) ne dépasse jamais 3,2 %. Mais pourquoi les différences entre valeurs de Black, Gram-Charlier et Johnson sont-elles plus importantes pour les valeurs d’endettement au pair? Au vu des développements de l’annexe, c’est la valeur temps du put de Johnson qui fait toute la différence. Comme pour toute option, cette valeur est la plus grande pour les valeurs au pair. Mais comme la valeur temps au pair est plus petite pour les valeurs du put de Johnson que pour celles des puts de Black et Gram-Charlier, il s’ensuit que c’est là que la différence de valeur temps est la plus grande. Aussi proposons-nous l’explication suivante : pour une distribution à asymétrie faible mais très leptocurtique, les valeurs du put de Johnson sont très rassemblées autour de la valeur moyenne d’une distribution qui ne présente que peu de volatilité. Les valeurs du put de Johnson sont alors inférieures à celles du put de Black basé sur deux paramètres ainsi qu’à celles du put de Gram-Charlier basé sur quatre paramètres car, dans le cas de Black, le coefficient d’aplatissement normal est de 3 et, dans le cas de Gram-Charlier sous contrainte, il est limité ici à 6,5. Les estimations de la simulation sont utilisées dans la section suivante pour calculer la charge en capital afférente au risque de crédit de l’engagement : le put de Johnson caractérise la procédure de valeur au modèle alors que les puts de Black et Gram-Charlier sont représentatifs de procédures NI avancées alternatives propres aux banques.
3. Engagements évalués à la valeur de modèle : préliminaires et implications pratiques
3.1 Préliminaires
Afin de positionner la « valeur au modèle » par rapport aux procédures réglementaires de Bâle-2, le document 2 présente comment calculer, selon les approches simplifiée et NI avancée, l’actif pondéré pour le risque (l’APR) des engagements hors bilan et des prêts au bilan. Tous les APRs représentent 12,5 fois les expressions E(1) à E(4) puisque le coefficient de capital minimum est de 8 %. Afin d’améliorer la comparabilité, nous faisons abstraction des garanties, des accords généraux de compensations ou des autres risques tels que légal, de marché, opérationnel, de réputation, etc. L’approche « valeur au modèle » consiste à remplacer en E(1) les coefficients comptables fixes et donnés (FCC et FPR) de l’approche Bâle-2 simplifiée par ceux (πT – j et PjT – j) présentés en E(2). Dans cette expression, le produit de L et πT – j définit l’exposition en cas de tirage (ECT) à la date d’audit, un concept très similaire à l’exposition en cas de défaut (ECD) pour les prêts au bilan en E(4). La relation entre les deux est la suivante : lorsque la ligne est tirée, le financement qui en découle devient un prêt au bilan exposé au défaut, comme n’importe quel prêt au comptant; la banque détient alors un call « vulnérable » puisque l’emprunteur est susceptible de faire défaut ultérieurement lors du remboursement du principal et/ou du paiement des intérêts du prêt. Quant à la portion non exercée des engagements, elle demeure encore sujette au tirage conditionnel ainsi qu’à la clause de « changement adverse significatif », et son put implicite continue à quantifier le coût notionnel de son risque de crédit. De plus, en introduisant à la sous-section 3.3, une correspondance biunivoque entre valeur d’endettement et cote de crédit des agences de notation externes, l’approche « valeur au modèle » extériorise les valeurs d’endettement. Ceci est similaire à l’approche des prêts au bilan sujets aux cotes de crédit des agences publiques en E(2). Au-delà du calcul d’une « juste » charge en capital correspondant au risque « réel » de crédit, la valeur au modèle sert aussi d’étalon de mesure pour calculer la réduction de capital que la procédure offre par rapport à l’approche simplifiée de Bâle-2 ou même par rapport à d’autres procédures NI avancées propres aux banques. Bien que le calcul soit basé sur les données canadiennes, il est tout à fait général : il ne tient pas compte des réglementations propres à certains pays, telles que celles du Canada, des États-Unis ou de l’Union Européenne.
Document 2
Normes de calcul de l’actif pondéré pour le risque de crédit (l’APR) du continuum du crédit commercial comprenant engagements hors bilan et prêts au bilan. Pour un coefficient de capital de 0,08, les APRs représentent 12,5 fois les diverses expressions ci-dessous
Note : Dans ces expressions, L désigne la valeur nominale de la ligne de crédit, FCC le facteur de conversion en crédit, FPR le facteur principal de risque, πT – j la proportion du tirage, PTj– j la valeur du put de Johnson à la date T – j, ECT l’exposition en cas de tirage, PD la probabilité de défaut, ECD l’exposition en cas de défaut, PCD la perte en cas de défaut, M un ajustement de durée et ρ le coefficient de corrélation. Lorsque les prêts sont corrélés, l’expression ρ ≈ 0,12(1 + exp(-50 × PD)) lie approximativement coefficient de corrélation et probabilité de défaut. L’expression E(4) se réécrit alors ECD × PCD × (CDPI – PD) × M, où CDPI désigne le cas de défaut le plus important; il y a alors un modèle de copule pour ρ ≠ 0.
3.2 Implication principale : de la « juste » charge en capital afférente au risque de crédit « réel » appréhendé par le put de Johnson
Le calcul de la « juste » charge en capital basée sur le risque de crédit appréhendé par le put de Johnson est présentée sous la colonne PJ du tableau 2 : celui-ci combine le scénario de référence du tableau 1 (F = 99 $ et T – j = 6 mois, avec une proportion de tirage πT – j de 60 %) avec le montant contractuel (139,7 milliards de $ présenté sur la première ligne du tableau 2) des engagements irrévocables courts en 2010 des six plus grandes banques canadiennes. Soit :
139,7 milliards de $ × 0,6 = 83,82 milliards de $
83,82 milliards de $ × 0,00985 (= valeur du put par milliard de $) = 825,627 millions de $
825,627 millions de $ × 0,08 = 66,05 millions de $.
Tableau 2
Comparaison sous Bâle-2 de la charge en capital afférente au risque de crédit d’engagements irrévocables à court terme : les « justes » charges selon les approches NI avancées de Johnson (valeur au modèle), de Gram-Charlier et de Black (modèles alternatifs propres aux banques) versus celle basée sur les coefficients comptables de l’approche Bâle-2 simplifiée
Notes : a PJ, PGC et PB indiquent que les calculs sont basés sur les valeurs des puts européens à terme de Johnson, Gram-Charlier et Black, respectivement.
b C’est le total des montants contractuels présentés dans les rapports annuels de 2010 des six plus grandes banques canadiennes.
Sur la première ligne, la proportion de tirage de 60 % convertit le montant contractuel des engagements en exposition en cas de tirage (ECT) à la date d’audit de Bâle-2. Cette exposition de 83,82 milliards de $ se substitue à l’équivalent-crédit de l’approche comptable de Bâle-2, soit le montant de 27,94 milliards de $ (139,7 milliards de $ × 0,2) qui est rapporté à la ligne (3) du tableau 2. Sur la deuxième ligne ci-dessus, la multiplication de l’ECT par la valeur du put de Johnson (le risque de crédit « réel » des engagements) détermine le montant des engagements irrévocables courts pondérés pour le risque, montant qui est aussi rapporté sur la ligne (5) du tableau 2. Ce montant de 825,627 millions de $ se substitue à celui de l’approche simplifiée, soit un montant de 27,94 milliards de $ présenté sur la ligne (5) du tableau 2. Enfin, sur la troisième ligne ci-dessus, la « juste » charge en capital s’obtient en appliquant le ratio en capital de 8 % au montant des engagements pondérés pour le risque : cette charge de 66,05 millions de $ est à comparer à celle de 2,235 milliards de $ (27,94 milliards de $ × 0,08) de l’approche Bâle-2 simplifiée, cette dernière étant rapportée sur la ligne (6) du tableau 2. Pour compléter notre argument, supposons maintenant que, lorsque les banques calculent la charge de capital afférente au risque de crédit de leurs engagements selon leur propre procédure NI avancée, certaines d’entre elles choisissent soit les valeurs des puts de Gram-Charlier soit celles de Black comme représentatives de leur risque de crédit réel (soit respectivement les valeurs de 1,127 $ et 1,114 $ dans le scénario de référence du tableau 1, c.-à-d. ici les valeurs de 0,01127 et 0,01132 par milliard de $). Les détails de ces calculs de charge en capital sont présentés sous les colonnes PGC et PB du tableau 2; et les montants de charges selon ces approches NI avancées sont de 75,57 millions de $ et de 74,7 millions de $, respectivement (ces deux chiffres étant présentés sur la ligne (6) du tableau 2). Ces données additionnelles nous permettent maintenant de procéder à la comparaison des diverses approches en choisissant la « valeur au modèle » comme étalon de mesure. Cette comparaison résulte en : (i) une réduction du capital requis de 2,1689 milliards de $ (2,235 – 0,06605) par rapport à l’approche Bâle-2 simplifiée (le montant se trouve à la ligne (9) du tableau 2), (ii) une diminution de 9,52 millions de $ (75,57 – 66,05) par rapport à la procédure NI avancée basée sur le put de Gram-Charlier (le montant se trouve à la ligne (7) du tableau), et (iii) une diminution de 8,65 millions de $ (74,7 – 66,05) par rapport à la procédure NI avancée basée sur le put de Black (le montant se trouve sur la ligne (8) du tableau). Depuis 2010 toutefois, toute diminution de charge en capital est réduite dans une certaine mesure par la nouvelle charge opérationnelle introduite par Bâle-2, charge dont nous ne tenons pas compte ici dans nos calculs (cf. concernant cette dernière, Chateau, 2009). Au vu de cette comparaison, les banques sont donc susceptibles de choisir la « valeur au modèle » basée sur le put de Johnson comme approche NI avancée « efficiente », et les régulateurs de Bâle-2 seront enclins à ratifier ce choix puisque les valeurs du put basées sur l’absence d’arbitrage imposent une discipline de quasi-marché dont les charges en capital réglementaire et économique sont identiques.
3.3 Seconde implication : de l’accroissement de charge en capital due à une diminution de la cote de crédit d’emprunteurs au taux de base variable
Cette application de la « valeur de modèle » permet de calculer l’accroissement de charge en capital induite par une baisse de la note de crédit d’un emprunteur qui est classifié par la banque comme étant au taux de base lors de la signature de l’engagement, mais qui se trouve être de facto plus risqué qu’au taux de base au cours de la vie de l’engagement. La charge en capital additionnelle due à cette évaluation bancaire adverse se calcule en trois étapes : choix d’une matrice de transition des cotes de crédit des emprunteurs, correspondance isomorphe entre déclins des cotes de risque et valeurs d’endettement progressivement en jeu, et combinaison de la matrice de transition avec celle du put de Johnson du tableau 1.
Lors de la première étape, il est souhaitable d’appréhender les baisses de cote de crédit des emprunteurs par une matrice de transition spécifique aux engagements de crédit. À notre connaissance, ce type d’information n’est toutefois pas publiquement disponible actuellement. Aussi, recourons-nous à une matrice de transition basée sur les cotes de crédit des obligations corporatives. Plus spécifiquement, nous choisissons les probabilités de transition annuelles du modèle de Xing et al. (2012) basées sur des chaînes de Markov qui tiennent compte des changements structurels stochastiques dans les probabilités de transition[15]. Cette matrice, basée sur les notations de crédit de Standard & Poor’s, couvre la période d’octobre 2008 à septembre 2009; dès lors, elle appréhende les changements structurels récents dans les cotes de crédit. Dans la partie supérieure du tableau 3, nous ne reproduisons que les probabilités de transition des cotes de crédit des obligations considérées comme acceptables pour investissement (investment grade). Cette matrice attribue une cote 3A à un emprunteur qui est classifié par la banque comme emprunteur au taux de base variable lors de la signature de l’engagement, avec une probabilité de 89,97 % de le demeurer pendant la période restante jusqu’à l’expiration de l’engagement. Mais supposons que 6 mois après la signature de l’engagement, la banque s’aperçoit qu’elle a mal évalué la fiabilité financière de l’emprunteur au taux de base, qui est de 2A au lieu de 3A. L’engagement étant irrévocable, l’emprunteur garde la marge initiale fixe de son taux de base m̅0, alors qu’il devrait normalement faire face à une marge supérieure, par exemple, marge de base + 50 points de base[16]. Puisque m̅0 < mj = m̅0 + 50 points, il s’en suit dans l’équation 1 que F = 99,5 $ < L = 100 $. En d’autres termes, une baisse de cote de crédit se traduisant par une marge supérieure à celle du taux de base entraîne une valeur d’endettement inférieure. La seconde étape est formalisée au début de la partie supérieure du tableau 3, où les valeurs d’engagement qui deviennent progressivement en jeu sont jumelées avec des cotes de crédit qui elles déclinent progressivement. Par souci de consistance interne du continuum de crédit commercial, cette correspondance est identique à celle qui fut adoptée en 2000 pour les prêts au bilan dans le second document consultatif du Basel Committee on Banking Supervision (2000). Dans une troisième étape finale, la correspondance entre valeurs d’endettement et cotes permet d’intégrer la matrice de transition de la partie supérieure avec la matrice PJ du tableau 1, cette dernière étant reproduite après transposition dans la partie inférieure du tableau 3.
Tableau 3
Combinaison de la matrice des probabilités de transition des notations de crédit de Xing et al. (2002)[a] (ne couvrant que les obligations acceptables pour investissement) pour la période d’octobre 2008 à septembre 2009 avec, dans la partie inférieure, la matrice PJ (transposée) des estimations du put européen à terme de Johnson du tableau 1
Moyennes postérieures des probabilités de transition (exprimées en pourcentage) estimées à partir du modèle de Xing et al., (2012), tableau 1, basé sur les notations de Standard & Poor’s; ce modèle tient compte des changements structurels stochastiques dans les probabilités de transitions de ces notations de crédit.
La translation introduit une correspondance isomorphe entre valeurs d’endettement à terme et notations de crédit.
Un exemple numérique nous permet d’illustrer le mode d’emploi du tableau 3. Supposons que, lors de la signature de l’engagement, la banque offre à l’emprunteur un engagement annuel de 100 $ dont la cote est 3A puisqu’il est considéré comme emprunteur au taux de base. Mais, lorsque la banque vérifie six mois plus tard sa fiabilité financière, elle constate que cette dernière a baissé d’un cran à 2A. Au vu de la partie supérieure du tableau 3, la probabilité de passer de 3A à 2A est de 9,45 % (en caractères gras), avec une baisse correspondante de la valeur d’endettement de 100 $ à 99,5 $. Pour le scénario de référence dans la partie inférieure (scénario dont la durée jusqu’à l’échéance est de six mois), le coût additionnel du risque de crédit par 100 $ d’engagement inutilisé est de (0,493 $ – 0,011 $) = 0,481 $. Dès lors, le coût attendu de cette diminution de notation d’un cran est de (0,481 $ × 0,0945) = 0,04545 $ ou près de 4,5 cents par 100 $ d’engagement de crédit. Examinons maintenant l’impact du coût additionnel dû à cette réduction de cote pour le montant contractuel des engagements du tableau 2. Supposons que 9,45 % des 139,7 milliards de $ d’engagements irrévocables courts, soit 13,2 milliards de $, subissent une baisse de cote d’un cran de 3A à 2A (il s’agit d’une approximation puisque tous ces engagements ne sont pas au taux de base). Le coût induit par cette baisse est de 600 millions de $ (13,2 milliards de $ × 0,04545 $), laquelle se traduit alors, pour les six banques à charte, par un accroissement de la charge en capital de 48 millions de $ (600 millions de $ × 0,08). En bref, en combinant la matrice de transmission de la partie supérieure du tableau avec les valeurs du put de Johnson dans sa partie inférieure, les banques sont à même de quantifier l’accroissement de charge en capital induite par une baisse de cote touchant une fraction de leurs engagements irrévocables courts. La translation des valeurs d’engagement en cote de crédit a aussi l’avantage de donner à la procédure interne de « valeur au modèle » une transparence externe, par le biais des agences de notation externes.
Conclusion
Cette recherche vise à rendre consistant le calcul de la charge en capital afférente au risque de crédit des composantes du continuum du crédit commercial, soit les engagements de crédit hors bilan et les prêts au bilan. Cette consistance s’obtient en sélectionnant le risque de crédit des engagements (par similitude avec celui des prêts commerciaux) au lieu de la durée initiale des engagements (comme prescrit par Bâle-2) comme déterminant principal du calcul. Pour y arriver, nous proposons l’approche « valeur au modèle » comme approche avancée fondée sur les notations internes (NI) : dans celle-ci, le risque de crédit de l’engagement est implicite à la valeur d’endettement à terme dont la distribution de Johnson est caractérisée par quatre paramètres. La « juste » charge en capital s’obtient alors en combinant le put à terme de Johnson (le risque de crédit « réel ») avec la proportion de tirage de la ligne de crédit suite à l’exercice de l’engagement. Comme cette « juste » charge est très modérée, la « valeur au modèle » constitue une approche NI avancée « efficiente » puisqu’elle offre une réduction de la charge en capital par rapport à celle calculée à partir de l’approche Bâle-2 simplifiée ou même par rapport à celles d’approches NI avancées alternatives où le risque de crédit est appréhendé par les puts de Black ou de Gram-Charlier. L’approche « valeur au modèle » permet aussi aux banques de déterminer la charge additionnelle en capital due à une dégradation de la cote de crédit de leurs emprunteurs. La procédure est basée sur la translation des valeurs d’endettement en cotes de crédit d’agences de notation externes, et ce, par l’entremise de probabilités de transition entre cotes de crédit en début et fin de période. En d’autres termes, l’approche « valeur au modèle » permet aux banques de quantifier l’impact d’un changement de cote de crédit de la signature de l’engagement jusqu’à sa charge finale additionnelle en capital. Toutefois, le calcul des valeurs d’endettement, des puts implicites et des proportions de tirage montre très clairement que l’approche de valeur au modèle, ou toute autre procédure NI avancée, requiert une vaste banque de données, sera compliquée et demandera du temps. L’une des premières extensions de la présente recherche sera de tenir compte des corrélations existantes dans le portefeuille des engagements de crédit de la banque.
Appendices
Annexe
L'annexe vise à trouver une distribution qui permette de tenir compte des coefficients d’aplatissement du document 1 supérieurs à 7, la borne supérieure de ce coefficient dans la distribution de Gram-Charlier sous contrainte. La solution se trouve dans un système de « translation » où la variable transformée z = h(x) est considérée comme ayant une distribution normale. Cette transformation basée sur quatre paramètres est introduite ensuite dans la condition de rémunération terminale de l’option que nous développons jusqu’à l’obtention de la forme analytique du put européen à terme. Passons maintenant aux développements.
Si la variable aléatoire h(x) est distribuée selon une loi normale, il est possible de trouver les valeurs γ et δ telles que z = γ + δh(x) suit une loi normale standard (par convention δ > 0). Remplaçons alors dans z, x par (x – ξ)/λ de sorte que
Selon (A.1), la distribution de x est déterminée par quatre paramètres, γ, δ, ξ, et λ (ce dernier doit être positif). Les valeurs de β1 et β2 (le carré du coefficient d’asymétrie et le coefficient d’aplatissement, respectivement) sont aussi définies par cette équation et plus spécifiquement par γ et δ. Dépendant du choix de la fonction h[.], le plan (β1, β2) est divisé en deux systèmes, borné SB et non borné SU, le système lognormal, SL, jouant le rôle de système de transition. Pour une discussion approfondie, on consultera Johnson (1949) ou Johnson, Kotz et Balakrishnan (1994).
Dans un système de courbes de fréquence, il nous faut commencer par déterminer quel système s’applique au problème sous considération : le système borné, SB, ou non borné, SU. Puisque dans le système lognormal SL, β1 contraint le coefficient d’aplatissement β2, déterminons la valeur d’une nouvelle variable ω en résolvant l’expression β1 = (ω – 1)(ω + 2)2. La seule racine réelle est
Mais d’après la définition du coefficient d’aplatissement,
![]() (l’estimation de β2) = ω4 + 2ω3 + 3ω2 – 3.
Si cette estimation est approximativement la même que celle de
β2, le système de translation approprié est le
système lognormal SL. Par contre, si
(l’estimation de β2) = ω4 + 2ω3 + 3ω2 – 3.
Si cette estimation est approximativement la même que celle de
β2, le système de translation approprié est le
système lognormal SL. Par contre, si ![]() , ce qui est toujours le cas pour nos engagements de
crédit, le système approprié est le système non borné SU.
, ce qui est toujours le cas pour nos engagements de
crédit, le système approprié est le système non borné SU.
Une fois le système SU choisi, passons au calcul de ses paramètres
γ, δ, ξ, et λ. Nous commençons par calculer γ et δ à partir de
![]() et β2. Si le coefficient d’aplatissement
est inférieur à 15, nous utilisons la table 35 de Johnson dans Pearson
et Hartley (1972); par contre, si le coefficient d’aplatissement est
supérieur à 15 (β2 pouvant atteindre une valeur de 36
dans le document 1), nous utilisons la procédure itérative d’Elderton et
Johnson (1969 : 126-128)[17]. L’attrait de
cette procédure est qu’elle accommode des valeurs du coefficient
d’aplatissement bien supérieures à 7, la limite supérieure de la
contrainte de Jondeau-Rockinger pour la distribution de Gram-Charlier.
Dès que nous avons les valeurs de γ et δ, nous pouvons calculer les deux
autres, celles de ξ et λ. Ceci revient à trouver les racines des
expressions suivantes :
et β2. Si le coefficient d’aplatissement
est inférieur à 15, nous utilisons la table 35 de Johnson dans Pearson
et Hartley (1972); par contre, si le coefficient d’aplatissement est
supérieur à 15 (β2 pouvant atteindre une valeur de 36
dans le document 1), nous utilisons la procédure itérative d’Elderton et
Johnson (1969 : 126-128)[17]. L’attrait de
cette procédure est qu’elle accommode des valeurs du coefficient
d’aplatissement bien supérieures à 7, la limite supérieure de la
contrainte de Jondeau-Rockinger pour la distribution de Gram-Charlier.
Dès que nous avons les valeurs de γ et δ, nous pouvons calculer les deux
autres, celles de ξ et λ. Ceci revient à trouver les racines des
expressions suivantes :
et
Au vu de ce qui précède, nous appliquons maintenant le système de
translation à la distribution de la valeur d’endettement à terme. De
façon plus précise, nous approximons la fonction de densité réelle de la
valeur d’endettement à terme, h(x) = h(F), par la densité approximée ![]() , sous la condition que les quatre premiers moments des
densités réelle et approximée soient identiques. Ceci se fait en
utilisant la famille de probabilité de Johnson à quatre variables
décrite ci-dessus, puisque la distribution peut être identifiée aux
quatre premiers moments de la densité de la vraie valeur d’endettement.
L’approche est similaire à celle de Guldiman (1997) ou Simonato (2011)
pour la valeur à risque et à celle de Posner et Milesky (1998) pour les
options exotiques. Pour notre système non borné SU, la transformation
appropriée de la distribution normale standard z est :
, sous la condition que les quatre premiers moments des
densités réelle et approximée soient identiques. Ceci se fait en
utilisant la famille de probabilité de Johnson à quatre variables
décrite ci-dessus, puisque la distribution peut être identifiée aux
quatre premiers moments de la densité de la vraie valeur d’endettement.
L’approche est similaire à celle de Guldiman (1997) ou Simonato (2011)
pour la valeur à risque et à celle de Posner et Milesky (1998) pour les
options exotiques. Pour notre système non borné SU, la transformation
appropriée de la distribution normale standard z est :
où sinh-1 désigne l’inverse de la fonction sinus hyperbolique. Dès lors
Définissons maintenant la valeur du put européen à terme de valeur d’exercice L pour la valeur x = F à la date T, c.-à-d. ici la valeur d’endettement à terme. Soit
où h(x) désigne la fonction de densité de
probabilité. Posons maintenant ![]() et intégrons (A.7) par partie.
Soit
et intégrons (A.7) par partie.
Soit
Remplaçons alors la distribution normale standard réelle de la valeur d’endettement à terme par celle approximée du système de Johnson. Soit
Comme le système non bornée SU s’applique aux valeurs d’endettement à terme leptocurtiques, l’expression (A.5) z = γ + δ sinh-1[(x – ξ)/λ] constitue la transformation appropriée de la distribution normale standard. Développons maintenant l’intégrale de l’expression (A.8). Soit
Posons maintenant ![]() , mettons-y x en
évidence et dérivons x par
rapport à ν. Soit respectivement
, mettons-y x en
évidence et dérivons x par
rapport à ν. Soit respectivement ![]() et
et ![]() . En tenant compte de ceci en (A.9), il vient que :
. En tenant compte de ceci en (A.9), il vient que :
où l’expression de droite est basée sur le fait que ![]() et que
et que ![]() . Puisque
. Puisque ![]() , l’expression (A.10) contient une
intégrale double qui se réécrit alors
, l’expression (A.10) contient une
intégrale double qui se réécrit alors
En (A.11), l’expression entre crochets contenant deux termes, nous développons le second terme (avant d’appliquer ensuite la même méthodologie au premier terme). Sans tenir compte de λ/2δ et en inversant l’ordre des intégrales du second terme, il vient alors que
Afin de développer en (A.12) l’intégrale de droite entre crochets,
nous posons ![]() d’où
d’où ![]() et donc
et donc
Substituons (A.13) en (A.12) pour obtenir
Considérons maintenant le premier des deux termes de l’intégrale en (A.14). Soit
Nous y complétons le carré pour les termes de l’exponentielle et réintégrons le résultat dans l’intégrale. Ceci donne
Procédons au changement de variable ![]() d’où dy = dz. Il
vient alors que
d’où dy = dz. Il
vient alors que
En procédant de façon identique pour le second terme de l’expression (A.14), il vient que
Nous collectons alors les termes des expressions (A.15) et (A.16), ce qui donne
Passons maintenant au développement du premier terme de l’expression (A.11) de façon similaire. Ce qui donne
Et en tenant compte de λ/2δ et des expressions (A.17) et (A.18), il vient alors que
Finalement, la valeur du put de l’expression (A.8) s’écrit :
Reprenons maintenant les premier et quatrième termes de (A.19) et développons. Soit :
où la dernière expression est obtenue par remplacement dans sinh(.)
de Q par ![]() . Enfin, par substitution de (A.20) dans
(A.19) où les deuxième et troisième termes sont
réarrangés, la forme analytique du put européen de la valeur d’endettement à terme
s’écrit :
. Enfin, par substitution de (A.20) dans
(A.19) où les deuxième et troisième termes sont
réarrangés, la forme analytique du put européen de la valeur d’endettement à terme
s’écrit :
où PJ désigne la valeur du put européen à terme de Johnson : c’est l’expression (8) présentée dans le texte. Afin de corroborer notre résultat obtenu en partant de la condition de rémunération du put européen à terme, nous utilisons l’expression analytique du call européen à terme dérivée par Posner et Milesky (1998 : 115-118, en combinant leurs équations (14) et (28)). Soit respectivement, adaptées au présent contexte, les expressions
et
Or, en substituant (A.21) dans la parité put-call à terme P = C + e-rT(L – F), nous retrouvons l’expression (A.20), le put européen à terme de Johnson.
Notes
-
[1]
Pour être bref partout, Bâle-2 fait référence en bibliographie à « Basel Committee on Banking Supervision » (2006) et Bâle-1 à « Basel Committee on Banking Supervision » (1988).
-
[2]
Au-delà de la distinction selon l’échéance initiale de l’engagement, Bâle-2 maintient aussi celle introduite par Bâle-1 entre engagements révocables et irrévocables : les premiers sont résiliables sans condition au gré de la banque en tout temps alors que les seconds ne le sont pas.
-
[3]
Les données proviennent des rapports annuels de 2010 des six plus grandes banques canadiennes : soit les Banques de Montréal et de Nouvelle Écosse, la CIBC, les Banques Nationale et Royale ainsi que TD Canada Trust. Les données afférentes aux engagements proviennent de la note aux états financiers consolidés « garanties, engagements et passifs éventuels » et celles concernant les prêts commerciaux se trouvent dans divers tableaux des données supplémentaires de la section « rapport de gestion » des rapports annuels.
-
[4]
L’approche Bâle-2 simplifiée laisse aussi inchangés les autres coefficients du risque de crédit des engagements introduits par Bâle-1 : les FCC et FRP demeurent nuls pour tous les engagements révocables quelle que soit leur échéance initiale, et les FCC de 50 % et FRP de 100 % demeurent aussi inchangés pour les engagements irrévocables dont la durée à courir jusqu’à l’échéance est à plus d’un an.
-
[5]
Toute réduction de charge de capital pour risque de crédit des engagements irrévocables courts est toutefois partiellement compensée par une nouvelle charge pour risque opérationnel introduite lors de Bâle-2. Nous ne traiterons pas explicitement de ce risque ici (cf. à cet effet, Chateau, 2009).
-
[6]
En l’absence d’un marché secondaire d’engagements de crédit, leur valeur n’est point déterminée par le marché mais par un modèle. D’où le terme « valeur au ou de modèle ».
-
[7]
Corrado et Su (1996) et Brown et Robinson (2002) examinent l’évaluation du call européen dont le sous-jacent présente une distribution asymétrique et leptocurtique. Ils utilisent une expansion en série du type A de Gram-Charlier de la fonction de densité normale lors de la dérivation de sa valeur analytique, laquelle intègre coefficients d’asymétrie et d’aplatissement. Parmi d’autres références sur le sujet, on consultera Knight et Satchell (1997), Bakshi et Madan (2000), Li (2000), Jondeau et Rockinger (2001), Backus etal. (2004), ou encore Rompolis et Tzavalis (2007).
-
[8]
Un taux variable se définit comme « coût de financement stochastique plus marge à terme fixe ». Sufi (2009) rapporte que, pour son échantillon de 4011 firmes publiques américaines couvrant la période de 1996 à 2003, les lignes de crédit représentent 74,8 % de leur financement bancaire; et la vaste majorité d’entre elles est à taux variable.
-
[9]
Libor et taux sur certificats de dépôt (CD) constituent d’autres indices exogènes.
-
[10]
Celle-ci est représentative de la marge récente comprise dans le taux de base variable au Canada (cf. à cet effet la sous-section 1.2 et le graphique 1). Pour les engagements hors taux de base, la marge de crédit comprend une marge de base fixe plus un ajout (+25 points de base, +50 points de base, et ainsi de suite). L’association de marges croissantes avec des notations de risque de crédit décroissantes est exploitée lors de la sous-section 3.3.
-
[11]
Quoique la présence d’une clause de changement adverse significatif rende les engagements résiliables du moins légalement, les banques s’abstiennent de faire jouer cette clause afin de ne point entamer leur capital de réputation (Boot et al., 1993).
-
[12]
Des valeurs fortement leptocurtiques se retrouvent ailleurs: témoin les valeurs de 10 rapportées par Jha et Kalimipalli (2010) concernant les distributions des rendements annuels sur l'indice S&P500 couvrant la période 1990 à 2002. Quant à Rompolis et Tzavalis (2007), ils obtiennent les coefficients d’aplatissement en neutralité au risque à partir des options sur l’indice S&P500 pour les années 1997 et 2001 : ceux-ci vont de 4,5 à 8,8. Enfin, Erikson et al. (2009) indiquent que la plupart des options aux États-Unis présentent des coefficients d’asymétrie et d’aplatissement dont les valeurs se trouvent en dehors de l’ellipse admissible de l’approche Gram-Charlier.
-
[13]
L'examen des déterminants du tirage (défaut, non-respect de conventions contraignantes (covenants) et baisse de la notation de crédit, entre autres) se situe au-delà du domaine de notre recherche. Consulter à cet effet, Agarwal et al. (2006), Jimenez et al. (2009), Sufi (2009) ou Norden et Weber (2010).
-
[14]
Comme il n’y a que trois valeurs d’endettement inférieures à 97,5 $ sur les 276 observations mensuelles, ces données aberrantes ne présentent que peu d’intérêt.
-
[15]
Nous supposons que les probabilités de transition annuelles s’appliquent aussi pour notre période plus courte de six mois. En ce qui concerne les matrices de transition alternatives, consulter, entre autres, Farnsworth et Li (2007), Kiefer et Larson (2007), Feng et al. (2008), Frydman et Schuermann (2008) ou encore Stefanescu et al. (2009).
-
[16]
Il existe plusieurs façons de calculer les différences de marges de l’équation 1 : (i) la marge fixe d’emprunteurs au taux de base moins celle au comptant d’emprunteurs à un taux plus risqué, (ii) la différence entre marges fixes d’emprunteurs au taux de base et à un taux plus risqué, ou (iii) la marge fixe moins la marge au comptant pour chaque classe d’emprunteurs. Concernant l’importance des différentiels de rendement entre les diverses catégories de notation de crédit S&P, on consultera Simkins et Rogers (2006).
-
[17]
Bowman et Shenton (1980), Shenton et Bowman (1982) et Tuenter (2001) constituent des approximations alternatives basées sur les fractions rationnelles, une expansion de Lagrange des paramètres, ou la détermination d’une racine, respectivement. Dans la table 35 de Pearson et Hartley, ainsi que lors des approximations d’Elderton-Johnson, Bowman-Shenton ou Tuenter, le signe de γ est l’opposé de celui de √β1 : pour une asymétrie négative γ est positif et, pour une asymétrie positive, il est négatif.
Bibliographie
- Agarwal, S., B.W. Ambrose et C. Liu (2006), « Credit Lines and Credit Utilization », Journal of Money, Credit and Banking, 38 : 1-22.
- Backus, D., S. Foresi et L. Wu (2004), « Accounting for Biases in Black-Scholes », Working Paper, Stern School of Business, New York University.
- Bakshi, G. et D. Madan (2000), « Spanning and Derivative-Security Valuation », Journal of Financial Economics, 55 : 205-238.
- BaselCommittee on Banking Supervision (1988), « International Convergence of Capital Measurement and Capital Standards », June, Bank for International Settlements.
- BaselCommittee on Banking Supervision (2000), « The Standardized Approach to Credit Risk », Bank for International Settlements.
- BaselCommittee on Banking Supervision (2006), « International Convergence of Capital Measurements and Capital Standards : A Revised Framework—Comprehensive Version », Bank for International Settlements, June, 239 pages.
- Black, F. (1976), « The Pricing of Commodity Contracts », Journal of Financial Economics, 3 : 167-179.
- Boot, A.W., S.I. Greenbaum et A.V. Thakor (1993), « Reputation and Discretion in Financial Contracting », American Economic Review, 83 : 1165-1183.
- Bowman, K.O. et L.R. Shenton (1980), « Evaluation of the Parameters of SU by Rational Fractions », Communications in Statistics, B9(2) : 127-132.
- Brown, C. et D. Robinson (2002), « Skewness and Kurtosis Implied by Option Prices », Journal of Financial Research, 25 : 279-281.
- Chateau, J.-P. (1990), « Valuation of ‘Capped’ Variable Rate Loan Commitments », Journal of Banking and Finance, 14 : 717-728.
- Chateau, J.-P. (2009), « Marking-to-Model Credit and Operational Risks of Loan Commitments : A Basel-2 Advanced Internal-Ratings Based Approach », International Review of Financial Analysis, 18 : 260-270.
- Chateau, J.-P. et D. Dufresne (2002), « The Stochastic-Volatility American Put Option of Banks’ Credit Line Commitments : Valuation and Policy », International Review of Financial Analysis, 11 : 159-181.
- Chateau, J.-P. et J. Wu (2007), « Basel-2 Capital Adequacy : Computing the ‘Fair’ Capital Charge for Loan Commitment ‘True’ Credit Risk », International Review of Financial Analysis, 16 : 1-21.
- Chava, S. et R. Jarrow (2007), « Modeling Loan Commitments », Finance Research Letters, 5 : 11-20.
- Corrado, C.J. (2007), « The Hidden Martingale Restriction in Gram-Charlier Option Prices », Journal of Futures Markets, 27 : 517-534.
- Corrado, C.J. et T. Su (1996), « Skewness and Kurtosis in S&P 500 Index Returns Implied by Option Prices », Journal of Financial Research, 19 : 175-192.
- Elderton, W.P. et N.L. Johnson (1969), Systems of Frequency Curves, Cambridge, University Press.
- Eriksson, A., E. Ghysels et F. Wang, (2009), « The Normal Inverse Gaussian Distribution and the Pricing of Derivatives ,» Journal of Derivatives, 16(3) : 23-37.
- Farnsworth, H. et T. Li (2007), « The Dynamics of Credit Spreads and Rating Migrations », Journal of Financial and Quantitative Analysis, 42 : 595-620.
- Feng, D., C. Gourieroux et J. Jasiak (2008), « The Ordered Qualitative Model for Credit Rating Transitions », Journal of Empirical Finance, 15 : 111-130.
- Frydman, H. et T. Schuermann (2008), « Credit Rating Dynamics and Markov Mixture Models », Journal of Banking and Finance, 32 : 1062-1072.
- Guldiman, T., (1997), RiskMetrics Technical Document, New York, Morgan Guarantee Trust Company.
- Hawkins, G.D. (1982), « An Analysis of Revolving Credit Agreements », Journal of Financial Economics, 10 : 59-81.
- Ho, T.S.Y. et A. Saunders (1983), « Fixed Rate Loan Commitments, Takedown Risk and the Dynamics of Hedging with Futures », Journal of Financial and Quantitative Analysis, 18 : 499-516.
- Hugston, L. et S. Turnbull (2001), « Credit Risk : Constructing the Basic Building Blocks », Economic Notes, 30 : 281-292.
- Hull, J.C. (2010), Risk Management and Financial Institutions, 2e édition, New Jersey, Pearson Prentice-Hall.
- Jarrow, R. et S. Turnbull (1995), « Pricing Derivatives on Financial Securities Subject to Credit Risk », Journal of Finance, 50 : 53-85.
- Jarrow, R., D. Lando et S. Turnbull (1997), « A Markov Model for the Term Structure of Credit Spreads », Review of Financial Studies, 10 : 481-523.
- Jha, R. et M. Kalimipalli (2010), « The Economic Significance of the Conditional Skewness in Index Option Markets », Journal of Futures Markets, 30 : 378-406.
- Jimenez, G., J.A. Lopez et J. Saurina (2009), « Empirical Analysis of Corporate Credit Lines », Review of Financial Studies, 22 : 5069-5098.
- Johnson, N.L. (1949), « Systems of Frequency Curves Generated by Methods of Translation », Biometrika, 36 : 149-176.
- Johnson, N., S. Kotz et N. Balakrishnan (1994), Continuous Univariate Distributions, 2nd Edition, New York, Wiley.
- Jondeau, E. et R. Rockinger (2001), « Gram-Charlier Densities », Journal of Economic Dynamics and Control, 25 : 1457-1483.
- Jurczenko, E., B. Maillet et B. Negrea (2004), « A Note on Skewness and Kurtosis Adjusted Option Pricing Models under the Martingale Measure », Quantitative Finance, 4 : 479-488.
- Kiefer, N.M. et C.E. Larson (2007), « A Simulation Estimator for Testing the Time Homogeneity of Credit Rating Transitions », Journal of Empirical Finance, 15 : 818-835.
- Knight, J. et S.E. Satchell (1997), « Pricing Derivatives Written on Assets with Arbitrary Skewness and Kurtosis » inKnight, J. et S.E. Satchell, (éds), Returns Distributions in Finance, Oxford, Butterworth-Heinemann.
- Li, F. (2000), « Option Pricing : How Flexible Should the SPD Be?», Journal of Derivatives, 7 : 49-65.
- Martin, J.S. et A.M. Santomero (1997), « Investment Opportunities and Corporate Demand for Lines of Credit », Journal of Banking and Finance, 21 : 1331-1350.
- Morgan, D.P. (1993), « Financial Contracts When Costs and Returns are Private », Journal of Monetary Economics, 31 : 129-146.
- Nawalka, S.K., G.M. Soto et N.K. Believa (2007), Dynamic Term Structure Modeling : The Fixed Income Valuation Course, New York, Wiley.
- Norden, L. et M. Weber (2010), « Credit Line Usage, Checking Account Activity, and Default Risk of Bank Borrowers », Review of Financial Studies, 23 : 3665-3699.
- Pearson, E.S. et H.O. Hartley (1972), Biometrika Tables for Statisticians, Vol. 2, Cambridge, University Press.
- Pennacchi, G. (2008), Asset Pricing, Boston, Pearson.
- Posner, S.E. et M.A. Milesky (1998), « Valuing Exotic Options by Approximating the SPD with Higher Moments », Journal of Financial Engineering, 7 : 109-125.
- Resti, A. (2009), « Exposure at Default, LGD and Recovery Risk », in R. Cont (éd.) Encyclopedia of Quantitative Finance, Chichester, Wiley.
- Rompolis, L.S. et E. Tzavalis (2007), « Retrieving Risk Neutral Densities based on Risk Neutral Moments through a Gram-Charlier Series Expansion », Mathematical and Computer Modelling, 46 : 225-234.
- Saunders, A. et M.M. Cornett (2010), Financial Institutions Management : A Risk Management Approach. 7e éd., New Jersey, Irwin/McGraw-Hill.
- Simkins, B.J. et D.A. Rogers (2006), « Asymmetric Information and Credit Quality : Evidence from Synthetic Fixed-Rate Financing », Journal of Futures Markets, 26 : 595-626.
- Simonato, J.-G. (2011), « The Performance of Johnson Distributions for Computing Value at Risk and Expected Shortfall », Journal of Derivatives, 19 : 7-24.
- Stanhouse, B., A. Schwarzkopf et M. Ingram (2011), « A Computational Approach to Pricing a Bank Credit Line », Journal of Banking and Finance, 35 : 1341-1351.
- Stefanescu, C., R. Tunaru et S. Turnbull (2009), « The Credit Rating Process and Estimation of Transition Probabilities : A Bayesian Approach », Journal of Empirical Finance, 16 : 216-248.
- Sufi, A. (2009), « Bank Lines of Credit in Corporate Finance : An Empirical Analysis », Review of Financial Studies, 22 : 1057-1088.
- Thakor, A.V. (1982), « Toward a Theory of Bank Loan Commitments », Journal of Banking and Finance, 6 : 55-84.
- Thakor, A.V., H. Hong et S.I. Greenbaum (1981), « Bank Loan Commitments and Interest Rate Volatility », Journal of Banking and Finance, 5 : 497-510.
- Tuenter, H. (2001), « An Algorithm to Determine the Parameters of SU-Curves in the Johnson System of Probability Distributions by Moment Matching », Journal of Statistical Computation and Simulation, 70 : 325-347.
- Xing, H., N. Sun et Y. Chen (2012), « Credit Rating Dynamics in the Presence of Unknown Structural Breaks», Journal of Banking and Finance, 36 : 78-89.
List of figures
Graphique 1
Taux de base, taux sur acceptations bancaires (AB) et marge de crédit, Canada, de 1988.01 à 2010.12
List of tables
Document 1
Analyse statistique des 276 observations mensuelles de la série chronologique des pourcentages de variations de la valeur d’endettement calculés à partir de l’équation 2 pour la période 1988.01 à 2010.12
Pour un échantillon de taille n = 276 observations, l’intervalle de confiance à 95 % des coefficients de Pearson d’asymétrie β1 et d’aplatissement β2 d’un échantillon de la distribution normale sont : ± 1,96(6/276)½ = ± 0,289 et 3 ± 1,96 (24/276)½ = 3 ± 0,578, respectivement.
Valeur mensuelle non biaisée (divisée par n – 1) × √12 = σ en pourcentage par année.
d.a. indique le nombre de données aberrantes ou de valeurs extrêmes (outliers).
Tableau 1
Valeurs des puts de Johnson, Black et Gram-Charlier implicites aux engagements de crédit irrévocables à court terme
Matrice Pj : les valeurs du put européen à terme de Johnson de l’équation 8.
Matrice PB : les valeurs du put européen à terme de Black de l’équation 3.
Matrice PGC : les valeurs du put à terme de Gram-Charlier de l’équation 4.
Définition des paramètres : F = valeur d’endettement à terme en $ calculée à partir de l’équation 1; L = 100 $, la valeur d’exercice de la ligne de crédit en $; r = le taux d’intérêt à court terme sans risque exprimé en % par année; T = date d’échéance de l’engagement; et T – j = durée à courir jusqu’à l’échéance du put, en mois.
Note : Paramètres communs : L = 100 $; r = 3 % par an; T – j = 3,..,9 mois, avec T = 12 mois.
Les valeurs des paramètres de volatilité, d’asymétrie et d’aplatissement sont celles des colonnes 3 à 5 du document 1.
Document 2
Normes de calcul de l’actif pondéré pour le risque de crédit (l’APR) du continuum du crédit commercial comprenant engagements hors bilan et prêts au bilan. Pour un coefficient de capital de 0,08, les APRs représentent 12,5 fois les diverses expressions ci-dessous
Note : Dans ces expressions, L désigne la valeur nominale de la ligne de crédit, FCC le facteur de conversion en crédit, FPR le facteur principal de risque, πT – j la proportion du tirage, PTj– j la valeur du put de Johnson à la date T – j, ECT l’exposition en cas de tirage, PD la probabilité de défaut, ECD l’exposition en cas de défaut, PCD la perte en cas de défaut, M un ajustement de durée et ρ le coefficient de corrélation. Lorsque les prêts sont corrélés, l’expression ρ ≈ 0,12(1 + exp(-50 × PD)) lie approximativement coefficient de corrélation et probabilité de défaut. L’expression E(4) se réécrit alors ECD × PCD × (CDPI – PD) × M, où CDPI désigne le cas de défaut le plus important; il y a alors un modèle de copule pour ρ ≠ 0.
Tableau 2
Comparaison sous Bâle-2 de la charge en capital afférente au risque de crédit d’engagements irrévocables à court terme : les « justes » charges selon les approches NI avancées de Johnson (valeur au modèle), de Gram-Charlier et de Black (modèles alternatifs propres aux banques) versus celle basée sur les coefficients comptables de l’approche Bâle-2 simplifiée
Tableau 3
Combinaison de la matrice des probabilités de transition des notations de crédit de Xing et al. (2002)[a] (ne couvrant que les obligations acceptables pour investissement) pour la période d’octobre 2008 à septembre 2009 avec, dans la partie inférieure, la matrice PJ (transposée) des estimations du put européen à terme de Johnson du tableau 1
Moyennes postérieures des probabilités de transition (exprimées en pourcentage) estimées à partir du modèle de Xing et al., (2012), tableau 1, basé sur les notations de Standard & Poor’s; ce modèle tient compte des changements structurels stochastiques dans les probabilités de transitions de ces notations de crédit.
La translation introduit une correspondance isomorphe entre valeurs d’endettement à terme et notations de crédit.