Abstracts
Résumé
Des études récentes suggèrent que la variance conditionnelle des rendements financiers est sujette à des sauts. Ce papier étend une procédure non paramétrique de détection de sauts développée par Delgado et Hidalgo (2000) à la détection de sauts dans la variance conditionnelle. Les résultats de simulation démontrent que cette procédure estime de façon raisonnable le nombre de sauts ainsi que leurs emplacements. L’application de cette procédure aux rendements journaliers sur l’indice S&P 500 révèle la présence de plusieurs sauts dans la variance conditionnelle.
Abstract
Recent work suggests that the conditional variance of financial returns may exhibit sudden jumps. This paper extends a non-parametric procedure to detect discontinuities in otherwise continuous functions of a random variable developed by Delgado and Hidalgo (1996) to the conditional variance. Simulation results show that the procedure provides reasonable estimates of the number and location of jumps. This procedure detects several jumps in the conditional variance of daily returns on the S&P 500 index.
Article body
Introduction
Au cours des 20 dernières années, beaucoup d’attention a été portée sur les propriétés des deuxièmes moments des données financières. Une modélisation adéquate de la variance conditionnelle est importante aux fins d’inférence statistique et la mise en application des modèles de valorisation des produits dérivés ou des stratégies de portefeuille. À ces fins, les modèles GARCH (Engle, 1982; Bollerslev, 1986) et à volatilité stochastique (SV) ont été largement analysés et utilisés pour modéliser les agglomérats de volatilité (volatility clustering) observés dans les données. L’importance de la modélisation de la variance des rendements financiers a été soulignée par l’attribution du prix Nobel 2003 à Robert Engle.
Récemment, une certaine attention a été dévolue à la possibilité que les séries financières soient sujettes à des sauts, soit dans leur niveau ou dans leur volatilité. Parmi ces travaux, on retrouve ceux de Lamoureux et Lastrapes (1990), Hamilton et Susmel (1994), Cai (1994), Dueker (1997) et Maheu et McCurdy (2000). L’avantage de ces modèles relativement aux modèles GARCH standards est qu’ils permettent un ajustement très rapide à des périodes de haute ou basse volatilité. Les modèles GARCH sont trop persistants pour capter une soudaine augmentation de la volatilité; de même, l’effet des chocs sur la volatilité s’amenuise trop lentement pour capturer certains épisodes historiques. De plus, ceux-ci peuvent représenter une explication pour la présence de mémoire longue que l’on retrouve dans les mesures de volatilité tel que décrite par Liu (2000). Les sauts ont aussi été ajoutés aux modèles en temps continu tel que les travaux de Bates (1996), Chernov, Gallant, Ghysels et Tauchen (2003), Andersen, Benzoni et Lund (2002), Pan (2002), Eraker, Johannes et Polson (2003), Eraker (2001), Johannes (2000) et Bandi et Nguyen (2000). Contrairement aux analyses non paramétriques de Johannes (2003) et Bandi et Nguyen (2000), l’analyse de cet article se fait dans le cadre d’un modèle en temps discret. Ceci permet une classe de modèles plus grande que les modèles de diffusion et s’étend de façon naturelle aux modèles multivariés.
Cet article développe une procédure non paramétrique de test de sauts dans la volatilité des marchés financiers. La méthodologie utilisée est une version modifiée de l’estimateur par noyau de Delgado et Hidalgo (1995, 2000). Étant donné le grand nombre de modèles paramétriques suggérés pour modéliser le mouvement dynamique de la variance conditionnelle, l’approche non paramétrique apparaît naturelle. Une mauvaise spécification de la partie continue de la variance conditionnelle pourrait se refléter comme une mauvaise inférence sur la présence de sauts. Le test est dérivé en utilisant des fenêtres unidirectionnelles, originellement introduites par Müller (1992), pour estimer la variance conditionnelle. Aux points où un saut a lieu, les valeurs estimées du côté gauche et du côté droit convergeront vers leurs limites respectives. La différence entre les deux nous permettra de détecter le saut à ce point.
Le reste de l’article est organisé de la façon suivante : la première section décrit la procédure non paramétrique pour détecter les sauts développée par Delgado et Hidalgo (2000) et son application à la détection des sauts dans la variance conditionnelle. Le comportement en échantillons finis de cette procédure est examiné à la section 2 via une analyse de Monte-Carlo. La troisième section présente les résultats empiriques en utilisant les rendements journaliers de l’indice du Standard and Poor’s 500. Finalement la dernière section renferme certaines conclusions qui se dégagent de l’analyse.
1. Détection de sauts non paramétrique dans la variance conditionnelle
Dans cette section, nous présentons notre procédure de détection des sauts dans la volatilité conditionnelle de façon non paramétrique. Le lecteur devrait se référer à l’article de Delgado et Hidalgo (2000) pour plus de détail sur la procédure. Nous allons nous concentrer sur le cas où le conditionnement se fait sur les valeurs retardées de la variable d’intérêt, par exemple, les rendements d’un actif financier.
Soit yt les rendements d’un actif financier. Nous allons estimer les moments conditionnels de yt en utilisant la représentation fonctionnelle :
où la variable aléatoire εt est supposée une différence de martingale de variance unitaire et indépendante de ht = E[u21t | Xt], la variance conditionnelle de yt et Xt = (yt-1, ..., yt-p, τ)′ est un vecteur de dimension p + 1 de p valeurs retardées de yt et de la fraction de l’échantillon ![]() . De plus nous allons décomposer l’espérance conditionnelle de yt en deux parties :
. De plus nous allons décomposer l’espérance conditionnelle de yt en deux parties :
où g1 est une fonction continue et ![]() sont les éléments de Xt autres que la tendance déterministe. La fonction
sont les éléments de Xt autres que la tendance déterministe. La fonction ![]() est une fonction escalier avec un nombre fini de sauts pour toutes valeurs des éléments de
est une fonction escalier avec un nombre fini de sauts pour toutes valeurs des éléments de ![]() Pour alléger la notation, nous allons dénoter
Pour alléger la notation, nous allons dénoter ![]() par S1t et u(Xt) par ut.
par S1t et u(Xt) par ut.
Avec cette décomposition, nous pouvons aussi écrire le carré de yt comme :
où m2(Xt) = m21(Xt) + ht et ![]() . Nous supposerons que nous avons aussi une décomposition pour l’espérance de y2t entre une partie continue et une fonction escalier :
. Nous supposerons que nous avons aussi une décomposition pour l’espérance de y2t entre une partie continue et une fonction escalier :
avec les généralisations de la notation ci-dessus. La variance conditionnelle peut être décomposée comme :
Le modèle suggéré est très général en termes du mécanisme menant aux changements de ![]() . L’utilisation du temps pour identifier les sauts ne signifie en aucun cas que nous croyons que le passage du temps est la source du déclenchement de sauts. Plutôt, toute variable causant les sauts devra être cohérente avec les résultats obtenus en supposant que le temps les cause. L’approche que nous utilisons est aussi assez riche pour regarder d’autres variables au lieu du temps comme variable identifiant les sauts. En particulier, un cas d’intérêt est celui où cette variable est une valeur retardée du processus yt, correspondant à un modèle à seuil.
. L’utilisation du temps pour identifier les sauts ne signifie en aucun cas que nous croyons que le passage du temps est la source du déclenchement de sauts. Plutôt, toute variable causant les sauts devra être cohérente avec les résultats obtenus en supposant que le temps les cause. L’approche que nous utilisons est aussi assez riche pour regarder d’autres variables au lieu du temps comme variable identifiant les sauts. En particulier, un cas d’intérêt est celui où cette variable est une valeur retardée du processus yt, correspondant à un modèle à seuil.
L’estimateur non paramétrique des moments conditionnels que nous allons examiner est l’estimateur par noyau de Nadaraya-Watson :
pour j = 1 ou 2 et où K : ℝp+1 → ℝ est un noyau et b est un paramètre contrôlant la largeur de la fenêtre. Par simplicité, nous allons restreindre l’analyse à des noyaux de forme multiplicative :
où k : ℝ → ℝ.
L’approche de Delgado et Hidalgo (2000) pour détecter les sauts consiste à regarder la différence entre les valeurs estimées par noyau avec des fenêtres unidirectionnelles pour toutes les valeurs de ![]()
et
avec  où le domaine de k–(·) est ℝ– et
où le domaine de k–(·) est ℝ– et  où le domaine de k+(·) est ℝ+.
où le domaine de k+(·) est ℝ+.
L’interprétation de l’estimateur m̂+j(τ, x͂) est une moyenne des valeurs de yjt pour les valeurs de ![]() plus grandes que τ, alors que m̂–j(τ, x͂) correspond à une moyenne des points où
plus grandes que τ, alors que m̂–j(τ, x͂) correspond à une moyenne des points où ![]() est plus petit que τ. Souvent, nous allons référer à ces estimateurs comme l’estimateur droit et l’estimateur gauche respectivement pour des raisons évidentes. Ces estimateurs ont été proposés par Müller (1992) avec
est plus petit que τ. Souvent, nous allons référer à ces estimateurs comme l’estimateur droit et l’estimateur gauche respectivement pour des raisons évidentes. Ces estimateurs ont été proposés par Müller (1992) avec ![]() seulement. Aux points de continuité de S1(·) et S2(·), les trois estimateurs vont converger vers la même quantité, mj(τ, x͂). Aux points où Sj(·) n’est pas continue, les trois estimateurs vont converger vers des valeurs différentes. L’estimateur bidirectionnel m̂j(τ, x͂) ne sera pas convergent dans ce cas mais convergera vers une moyenne pondérée des limites gauche et droite.
seulement. Aux points de continuité de S1(·) et S2(·), les trois estimateurs vont converger vers la même quantité, mj(τ, x͂). Aux points où Sj(·) n’est pas continue, les trois estimateurs vont converger vers des valeurs différentes. L’estimateur bidirectionnel m̂j(τ, x͂) ne sera pas convergent dans ce cas mais convergera vers une moyenne pondérée des limites gauche et droite.
La variance conditionnelle peut donc être estimée en utilisant les noyaux unidirectionnels :
où la notation « ± » réfère à l’estimateur droite et gauche simultanément. La version bidirectionnelle de cet estimateur a été traitée en détail par Masry et Tjϕstheim (1995). Le comportement individuel de m̂±2(τ, x͂) et m̂±1(τ, x͂) est obtenu directement de l’analyse de Delgado et Hidalgo (2000). Cependant, le comportement asymptotique de ĥ±(τ, x͂) est compliqué par la présence de corrélation entre les deux termes qui le composent.
Pour estimer les sauts, nous avons besoin de regarder la différence entre l’estimateur gauche et l’estimateur droit de h(τ, x͂). Soit le processus :
Notre cadre d’analyse est applicable à des sauts multiples et ceux-ci peuvent être estimés de façon séquentielle. Supposons qu’il y a M sauts, la valeur de M étant connue pour l’instant mais qui sera estimée plus tard. Le processus de sauts est donc :
avec la magnitude des sauts satisfaisant Δ1 > ... > ΔM sans perte de généralité.
L’estimateur du point où a lieu le premier saut est ![]() où Q = [τ̱, τ̄] pour τ̱, τ̄ ∈ (0, 1). Après que ce premier saut est estimé par τ̂1, le deuxième saut est estimé de la même façon mais où la maximisation se fait sur un intervalle plus restreint. En utilisant une borne presque sûre dérivée par Yin (1988), nous pouvons restreindre l’intervalle de recherche pour éviter la présence d’un autre saut dans les parages du saut estimé. Lors de l’estimation du kième saut, la recherche se fait sur l’intervalle Qk = Q – ∪k-1j=1Qj où Qj = [τ̂j – 2b, τ̂j + 2b].
où Q = [τ̱, τ̄] pour τ̱, τ̄ ∈ (0, 1). Après que ce premier saut est estimé par τ̂1, le deuxième saut est estimé de la même façon mais où la maximisation se fait sur un intervalle plus restreint. En utilisant une borne presque sûre dérivée par Yin (1988), nous pouvons restreindre l’intervalle de recherche pour éviter la présence d’un autre saut dans les parages du saut estimé. Lors de l’estimation du kième saut, la recherche se fait sur l’intervalle Qk = Q – ∪k-1j=1Qj où Qj = [τ̂j – 2b, τ̂j + 2b].
La loi des sauts estimés par cette procédure est contenue dans le prochain théorème :
Théorème 1 : Sous les hypothèses C1-C6 et B1-B4 et B6 de Delgado et Hidalgo (2000) et avec la décomposition (1), avec τ̂k ∈ int (Qk),
où
f–(τk, x͂2) est la densité à la gauche de τkévaluée au point (τk, x͂2),
f+(τk, x͂1) est la densité à la droite de τkévaluée au point (τk, x͂1),
γ(0) = ∫[K–(ν)]2dν, l’intégrale du carré du noyau gauche,
![]()
Il faut noter que la vitesse de convergence de ![]() dans ce théorème est plus lente que le taux usuel de
dans ce théorème est plus lente que le taux usuel de ![]() obtenu dans les modèles paramétriques[1]. Cependant, contrairement aux modèles paramétriques (par exemple Bai, 1997 et Bai et Perron, 1998), l’absence ou la présence d’autres sauts n’affecte pas le comportement des estimateurs des sauts. Ceci est dû à la nature locale de l’estimation par noyau.
obtenu dans les modèles paramétriques[1]. Cependant, contrairement aux modèles paramétriques (par exemple Bai, 1997 et Bai et Perron, 1998), l’absence ou la présence d’autres sauts n’affecte pas le comportement des estimateurs des sauts. Ceci est dû à la nature locale de l’estimation par noyau.
Il faut de plus remarquer que si l’on est prêt à supposer que l’espérance conditionnelle est continue, le problème se simplifie grandement car les estimateurs de l’espérance s’annulent dans la définition de ![]() si m̂+1 = m̂–1 = m̂1. Dans cette situation, on peut rechercher les sauts dans la variance conditionnelle en cherchant des sauts dans y2t seulement puisque
si m̂+1 = m̂–1 = m̂1. Dans cette situation, on peut rechercher les sauts dans la variance conditionnelle en cherchant des sauts dans y2t seulement puisque ![]() ne dépend pas de l’espérance et utiliser les résultats de Delgado et Hidalgo (2000) directement. Une autre alternative est d’utiliser un modèle paramétrique pour l’espérance, tel un modèle ARMA ou un modèle à changements de régimes markoviens. Dans ce cas aussi, la loi de
ne dépend pas de l’espérance et utiliser les résultats de Delgado et Hidalgo (2000) directement. Une autre alternative est d’utiliser un modèle paramétrique pour l’espérance, tel un modèle ARMA ou un modèle à changements de régimes markoviens. Dans ce cas aussi, la loi de ![]() ne dépend pas de l’estimateur de l’espérance car l’estimateur paramétrique de l’espérance converge à un taux plus rapide que l’estimateur non paramétrique des moments supérieurs.
ne dépend pas de l’estimateur de l’espérance car l’estimateur paramétrique de l’espérance converge à un taux plus rapide que l’estimateur non paramétrique des moments supérieurs.
Dans le résultat précédant, le nombre de sauts, M, était supposé connu, une situation improbable en pratique. Le théorème ci-dessus suggère un sup test pour la présence de j – 1 sauts contre l’alternative de j sauts (ou de façon équivalente un test de l’hypothèse nulle que Δ(τj) = 0). Soit la statistique :
où ![]() qui est simplement la plus grande valeur absolue de la statistique de Student pour l’hypothèse Δ(τj) = 0. La loi de ce test est :
qui est simplement la plus grande valeur absolue de la statistique de Student pour l’hypothèse Δ(τj) = 0. La loi de ce test est :
Théorème 2 : Sous les mêmes hypothèses que le théorème ci-dessus et ∫ k+(u) k(1)+(u) du = 0, si Δ(τk) = 0, lorsqueT → ∞
où est la mesure de Lebesgue
est la mesure de Lebesgue
et
La démonstration de ce théorème suit celle de Delgado et Hidalgo (1995) et est donc omise.
Une règle d’arrêt doit être choisie. Une possibilité est d’arrêter si la p-value du test ci-dessus est plus grande qu’un niveau prédéterminé. Malheureusement, cette approche n’estimera pas M de façon convergente car à chaque étape, il y a toujours une probabilité positive de rejeter l’hypothèse nulle, peu importe la taille de l’échantillon. Ainsi lorsque la procédure arrive à l’étape M + 1, le test de M + 1 contre M sauts donne une probabilité non nulle de rejeter l’hypothèse nulle et de conclure à la présence d’un saut additionnel. Donc, le nombre de sauts estimé avec cette approche sera biaisé vers le haut. Pour un test de niveau α, la probabilité de surestimer M de j sauts est égale à αj. Avec les niveaux habituellement utilisés, ceci tend vers 0 très rapidement. Une approche alternative à un niveau de test fixe est de faire tendre α vers 0 lorsque la taille de l’échantillon tend vers l’infini à un taux approprié.
La méthode proposée ici souffre de certaines difficultés. À cause de la nécessité de négliger une partie des observations autour des sauts estimés avant d’estimer le prochain saut, la procédure ne sera pas capable d’identifier des sauts qui sont très près l’un de l’autre ou qui sont renversés rapidement. La procédure est donc plus appropriée pour détecter des changements de régimes qui durent longtemps. De plus, nous supposons que yt et y2t peuvent être représentés par une fonction d’un petit nombre de variables retardées. Certains modèles paramétriques, tel que le modèle GARCH, impliquent que y2t est une fonction de son passé infini. Dans ce cas, notre estimateur non paramétrique ne pourra donner une description satisfaisante du comportement de la variance conditionnelle.
2. Résultats de Monte-Carlo
Dans cette section, nous allons présenter les résultats d’une petite expérience de Monte-Carlo. En particulier, nous voulons regarder le nombre de sauts détectés, correctement et incorrectement, la sensibilité des résultats au choix du nombre de retard et de la fenêtre et le comportement des sauts estimés.
Pour rendre l’expérience réaliste, nous utilisons le très populaire modèle GARCH(1,1) :
Les valeurs utilisées sont celles obtenues par l’estimation du modèle en utilisant les données de la section suivante, soit des rendements journaliers sur l’indice S&P 500 entre le 2 janvier 1980 et le 29 décembre 2000 pour un total de 5 308 observations. Les données sont présentées dans le graphique 1.
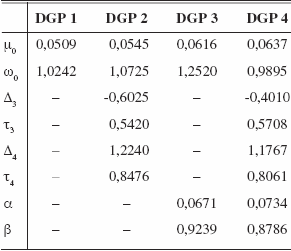
Nous utilisons quatre jeux de paramètres afin de vérifier le niveau et la puissance de notre procédure. La constante de l’équation de la variance conditionnelle est soit constante ou sujette à deux sauts :
et pour deux expériences nous enlevons les effets GARCH (α = β = 0) avec soit ωt constant ou sujet à deux sauts. La valeur des paramètres estimés se trouvent au tableau 1.
Graphique 1
Rendements journaliers sur l’indice S&P 500 – 1980-2000
Tableau 1
Valeurs des paramètres pour les expériences de simulation — valeurs estimées des rendements sur l’indice S&P 500 (2 janvier 1980–29 décembre 2000)
Avec tous ces jeux de paramètres, la condition pour que le quatrième moment de yt soit fini est satisfaite. La loi de εt est supposée N(0, 1) et la taille d’échantillon est T = 500. Chaque expérience est répétée 1 000 fois.
La fenêtre est choisie selon ![]() où c est une constante, σ̂j est l’écart-type estimé de la variable j et p est le nombre de retard dans l’ensemble de conditionnement. Nous utilisons une règle basée sur les données pour choisir c, soit une variation du critère de validation croisée :
où c est une constante, σ̂j est l’écart-type estimé de la variable j et p est le nombre de retard dans l’ensemble de conditionnement. Nous utilisons une règle basée sur les données pour choisir c, soit une variation du critère de validation croisée :
Ce critère ne considère que l’ajustement du deuxième moment de yt. Nous pourrions généraliser pour incorporer l’ajustement de l’espérance conditionnelle aussi mais la différence en pratique est tellement faible que nous utilisons la version plus simple ci-dessus. La constante c peut prendre des valeurs entre 0,8 et 1,2 en incrément de 0,1. Finalement, le noyau omnidirectionnel est k+(x) = x(3 – x) e-x 1(x ≥ 0), alors que le noyau bidirectionnel est gaussien. Tous les tests sont faits à un niveau de 5 % avec la normalité des erreurs imposée et 10 % des observations sont enlevées au début et à la fin de l’échantillon, c.-à-d. τ̱ = 0,1 et τ̄ = 0,9.
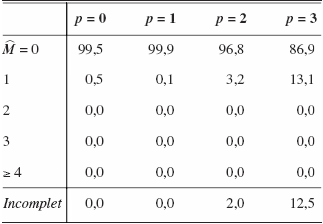
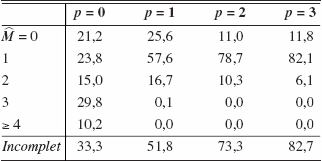
Les résultats du premier modèle (avec variance constante et donc sans sauts) sont présentés au tableau 2. Chaque colonne de ce tableau (et des suivants) nous montre la fréquence avec laquelle chaque nombre de sauts a été sélectionné sur la base de notre test suggéré ci-dessus pour un nombre de retards donné. La dernière rangée du tableau nous montre la fréquence où la procédure a arrêté avant d’obtenir une p-value plus grande que 5 % car il n’y avait plus assez de données disponibles. Ce tableau nous montre bien que si aucun saut n’existe, cette procédure ne nous donnera pas de faux signal. Il y a un peu de distorsion de niveau pour p = 3 qui est probablement due à l’imprécision de l’estimateur par noyau dans ce cas.
Les résultats pour le deuxième modèle sont présentés au tableau 3 et graphiques 2 et 3. Dans ce cas, il y a deux sauts dans la variance à 54,2 % et 84,8 % de l’échantillon. Sans valeur retardée des rendements, la procédure indique correctement la présence de sauts (dans une proportion de 98,5 % des cas). Elle estime le bon nombre de sauts dans la majorité des cas. Pour p ≥ 1, le nombre de sauts estimés est trop faible et la procédure semble manquer de puissance.
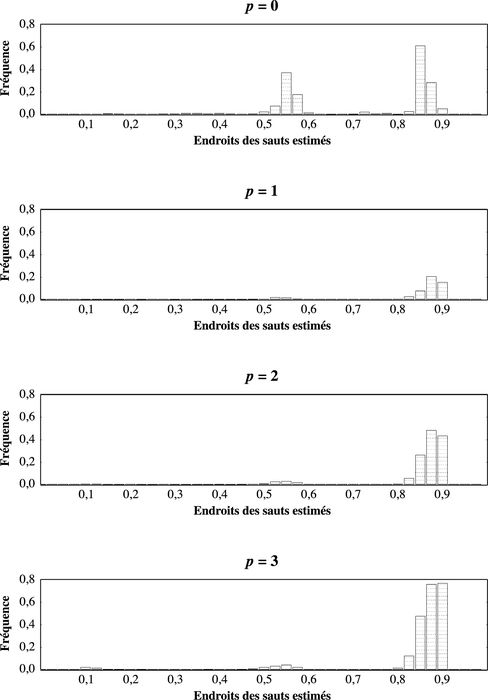
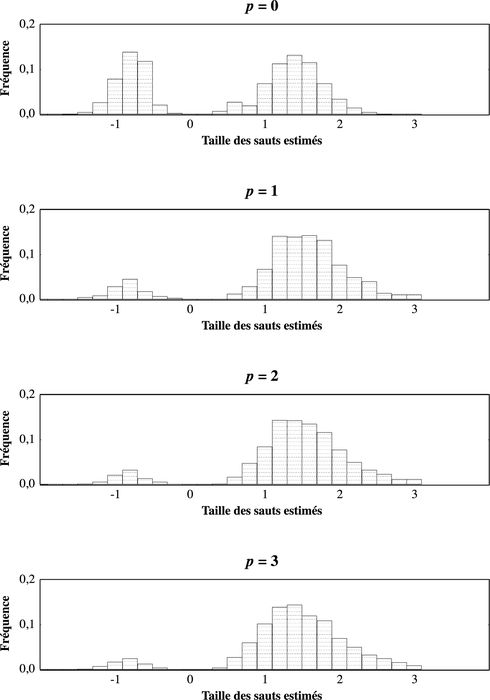
Le graphique 2 présente l’endroit des sauts estimés (les τ̂) pour les sauts trouvés significatifs lors de la simulation. Le saut à la fin de l’échantillon est dominant et celui-ci est bien estimé, sauf peut-être pour p = 3. Le deuxième saut est aussi bien estimé mais il y a peu de points dans cette région sauf pour p = 0, étant donné la faible puissance du test. La taille des sauts significatifs est présentée au graphique 3. La taille des deux sauts est très bien estimée avec évidemment moins de points autour du deuxième saut.
Tableau 2
Fréquence du nombre de sauts estimés pour DGP 1 (Le vrai nombre de sauts est zéro.)
Tableau 3
Fréquence du nombre de sauts estimés pour DGP 2 (Le vrai nombre de sauts est deux.)
Graphique 2
Distribution de l’endroit des sauts estimés – DGP 2
Graphique 3
Distribution de la taille des sauts estimés – DGP 2
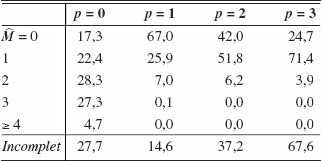
Les deux autres expériences incorporent des effets GARCH dans la variance conditionnelle. La troisième expérience est un modèle GARCH(1,1) standard dont les paramètres sont représentatifs, α = 0,0671 et β = 0,9239. Dans ce cas, la variance conditionnelle est une fonction du passé complet des rendements et donc il n’est pas surprenant que le noyau ne puisse l’estimer correctement. Ceci est une autre démonstration de la malédiction de la dimension (curse of dimensionality). Il est donc tout à fait attendu que notre test suggère la présence de sauts même si aucun n’existe. Ceci montre donc l’importance d’une faible persistance de la variance conditionnelle afin d’obtenir des résultats fiables.
Tableau 4
Fréquence du nombre de sauts estimés pour DGP 3 (Le vrai nombre de sauts est zéro.)
Finalement, la dernière expérience est un modèle GARCH(1,1) avec deux sauts. Encore une fois, le test n’est pas extrêmement fiable car le noyau ne peut approcher le comportement de la variance conditionnelle correctement. Cependant, les graphiques 4 et 5 nous montrent que les points de sauts sont surestimés alors que la taille des sauts est sous-estimée.
Tableau 5
Fréquence du nombre de sauts estimés pour DGP 4 (Le vrai nombre de sauts est deux.)
Graphique 4
Distribution de l’endroit des sauts estimés – DGP 4
Graphique 5
Distribution de la taille des sauts estimés – DGP 4
Pour conclure, il semble important de bien modéliser la dynamique de la variance conditionnelle afin de permettre de faire de l’inférence fiable. Dans les deux expériences où celle-ci n’est pas correctement capturée par un noyau avec un petit nombre de retards, on remarque une grande imprécision du nombre de sauts estimés. Malgré tout, le moment et la magnitude des sauts sont bien estimés. Il semble donc que le test suggéré ici pourrait être amélioré mais que l’estimation se fait de façon assez précise. Bien sûr, les résultats théoriques suggèrent qu’il doit exister une taille d’échantillon suffisamment grande pour que notre méthode puisse bien fonctionner même dans les cas où la variance conditionnelle est très persistante. Le même problème se pose lors de l’estimation d’une densité et dans ce cas, la perte de précision provenant d’une dimension élevée est quantifiée par Silverman (1986). Il est possible de contourner ce problème en imposant une structure plus forte au modèle comme le font Linton et Mammen (2003) pour la variance conditionnelle, mais une telle approche ne semble pas possible avec la présence de sauts. Une approche alternative est d’augmenter l’information disponible en analysant des données à haute fréquence comme Barndorff-Nielsen et Shephard (2003) ou Andersen, Bollerslev et Diebold (2003).
3. Résultats empiriques
Dans cette section, nous appliquons notre procédure de détection de sauts à la série des rendements journaliers sur l’indice S&P 500 du 2 janvier 1980 au 29 décembre 2000, utilisés pour définir les processus de génération des données pour les expériences de simulation ci-dessus. L’échantillon inclut 5 308 observations.
La procédure de détection est mise en application de la même façon que pour l’expérience de simulation avec jusqu’à trois valeurs retardées de y3t dans l’ensemble d’information. Les moments E(εt) et E(ε4t – 1) sont estimés en utilisant un noyau bidirectionnel et en utilisant les données restantes après avoir enlevé deux fois la fenêtre de chaque côté des sauts estimés. L’utilisation d’un noyau bidirectionnel donne des estimations des moments plus stables.
Les résultats sont présentés au tableau 6. Dans les quatre cas, la procédure termine avant d’obtenir une p-value plus grande que 5 % ce qui indique la présence de nombreux sauts. Les résultats sont intéressants car plusieurs dates reviennent souvent, en particulier la fin 1986, août 1990 et automne 1997.
Le saut de la fin de 1986 a lieu quelques mois avant le krach de 1987 et apparaît comme naturel. Il semble donc que la volatilité avait augmenté bien avant octobre 1987. Le saut en août 1990 coïncide avec l’invasion du Koweït par l’Irak. Il faut cependant noter que ce saut est négatif, c’est à-dire une baisse soudaine de la volatilité. Ces dates correspondent aussi aux conclusions de Eraker, Johannes et Polson (2002). En analysant trois périodes spécifiques (octobre 1987, octobre 1997 et automne 1998), ils attribuent une grande partie de la volatilité de ces périodes à des sauts de volatilité.
Tableau 6
Résultats de l’estimation de sauts dans la variance conditionnelle – rendements sur l’indice S&P 500, 2 janvier 1980–29 décembre 2000)
Si la présence de sauts dans la volatilité est fortement suggérée, sa portée économique reste cependant à juger. Une dimension intéressante est de regarder l’impact de sauts sur la valorisation d’options comme dans les articles de Eraker, Johannes et Polson (2002) et Eraker (2001). Il semble difficile de le faire dans le cadre d’analyse utilisé ici.
Conclusion
Cet article développe une procédure non paramétrique pour détecter des sauts dans la variance conditionnelle. Une étude de Monte-Carlo suggère que cette procédure estime bien l’endroit et la taille des sauts et qu’elle estime le nombre de sauts de façon adéquate si la dynamique de la variance conditionnelle est bien spécifiée.
Nos résultats empiriques suggèrent la présence de sauts dans la volatilité des rendements boursiers journaliers lors de plusieurs périodes historiques. Ces découvertes portent ombrage à la pratique courante d’utiliser un modèle tel que le GARCH(1,1) qui dépend de fa çon continue des rendements passés. L’impact économique sur la valorisation d’actifs et la gestion de portefeuille restent à quantifier.
Appendices
Annexe
Annexe
Démonstration du théorème 1
Premièrement, définissons ![]() et
et ![]() . Les résultats du théorème 4 de Delgado et Hidalgo (2000) et la méthode de Cramer-Wold nous donnent directement que le vecteur
. Les résultats du théorème 4 de Delgado et Hidalgo (2000) et la méthode de Cramer-Wold nous donnent directement que le vecteur ![]() a la loi :
a la loi :
et où la covariance est calculée selon :
En utilisant la décomposition des rendements (1), nous pouvons simplifier les termes dans la matrice de covariance. En particulier :
alors que
et
En utilisant le fait que εt est une différence de martingale avec variance égale à 1, chaque terme est :
et donc ![]() .
.
Nous pouvons finalement linéariser la fonction ![]() :
:
et obtenir :
où
∎
Remerciements
Je remercie un arbitre, Peter Phillips, Oliver Linton, Don Andrews et les participants à un séminaire à Yale et à l’Atelier canadien d’économétrie de 1998 pour leurs commentaires. Toutes les erreurs restantes sont évidemment ma seule responsabilité. Cette recherche a été rendue possible grâce au soutien financier d’une bourse Alfred P. Sloan, du CRSH et du Fonds FCAR.
Note
-
[1]
Loader (1996) développe une procédure alternative qui converge à la vitesse
 . Cependant, celle-ci requiert de mettre un poids non nul à l’observation courante lors de l’estimation ce qui est indésirable dans ce cas. Voir Pagan et Hong (1991) pour ce point.
. Cependant, celle-ci requiert de mettre un poids non nul à l’observation courante lors de l’estimation ce qui est indésirable dans ce cas. Voir Pagan et Hong (1991) pour ce point.
Bibliographie
- Andersen, T., L. Benzoni et J. Lund (2002), « An Empirical Investigation of Continuous-Time Models for Equity Returns », Journal of Finance, 57 : 1 239-1 284.
- Andersen, T.G., T. Bollerslev et F. X. Diebold (2003), « Some Like it Smooth, and Some Like it Rough: Untangling Continuous and Jump Components in Measuring, Modeling, and Forecasting Asset Return Volatility », Mimeo.
- Bai, J. (1997), « Estimating Multiple Breaks One at a Time », Econometric Theory, 13 : 315-352.
- Bai, J. et P. Perron (1998), « Estimating and Testing Linear Models with Multiple Structural Changes », Econometrica, 66 : 47-78.
- Bandi, F. et T. Nguyen (2003), « On the Functional Estimation of Jump-diffusion Models », Journal of Econometrics, 116 : 293-328.
- Barndorff-Nielsen, O. et N. Shephard (2003), « Power and Bipower Variation with Stochastic Volatility and Jumps », Mimeo.
- Bates, D. S. (1996), « Jumps and Stochastic Volatility: Exchange Rate Processes Implicit in Deutsche Mark Options », Review of Financial Studies, 9 : 69-107.
- Bollerslev, T. (1986), « Generalized Conditional Heteroskedasticity », Journal of Econometrics, 31 : 307-327.
- Cai, J. (1994), « A Markov Model of Switching-Regime ARCH », Journal of Business and Economic Statistics, 12 : 309-316.
- Chernov, M. R. Gallant, E. Ghysels et G. Tauchen (2003), « Alternative Models for Stock Price Dynamics », Journal of Econometrics, 116 : 225-257.
- Delgado, M. A. et J. Hidalgo (2000), « Nonparametric Inference on Structural Breaks », Journal of Econometrics, 96 : 113-144.
- Delgado, M. A. et J. Hidalgo (1995), « Nonparametric Inference on Structural Breaks », Mimeo.
- Dueker, M. J. (1997), « Markov Switching in GARCH Processes and Mean-Reverting Stock-Market Volatility », Journal of Business and Economics Statistics, 15 : 26-34.
- Engle, R. F. (1982), « Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of U.K. Inflation », Econometrica, 50 : 987-1 008.
- Eraker, B. (2004), « Do Stock Prices and Volatility Jump? Reconciling Evidence from Spot and Option Prices », Journal of Finance, à paraître.
- Eraker, B., M. Johannes et N. Polson (2003), « The Impact of Jumps in Volatility and Returns », Journal of Finance, 53 : 1 269-1 300.
- Hamilton, J. D. et R. Susmel (1994), « Autoregressive Conditional Heteroskedasticity and Changes in Regime », Journal of Econometrics, 64 : 307-333.
- Johannes, M. (2004), « The Statistical and Economic Role of Jumps in Interest Rates », Journal of Finance, à paraître.
- Lamoureux, C. G. et W. D. Lastrapes (1990), « Persistence in Variance, Structural Change, and the GARCH Model », Journal of Business and Economic Statistics, 8 : 225-234.
- Linton, O. et E. Mammen (2003), « Estimating Semiparametric ARCH (∞) Models by Kernel Smoothing Methods », Mimeo.
- Linton, O. et J. P. Nielsen (1995), « A Kernel Method of Estimating Structured Nonparametric Regression Based on Marginal Integration », Biometrika, 82 : 93-100.
- Liu, M. (2000), « Modeling Long Memory In Stock Market Volatility », Journal of Econometrics, 99 : 139-171.
- Loader, C. R. (1996), « Change Point Estimation Using Nonparametric Regression », Annals of Statistics, 24 : 1 667-1 678.
- Maheu J. M. et T. H. McCurdy (2000), « Identifying Bull and Bear Markets in Stock Return », Journal of Business and Economic Statistics, 18 : 100-112.
- Masry, Elias et Dag Tjϕstheim (1995), « Nonparametric Estimation and Identification of Nonlinear ARCH Time Series », Econometric Theory, 11 : 258-289.
- Müller, H.-G. (1992), « Change-Points in Nonparametric Regression Analysis », Annals of Statistics, 20 : 737-761.
- Pagan, A. R. et Y. S. Hong (1991), « Nonparametric Estimation and the Risk Premium » in W. A. Barnett, J. Powell et G. E. Tauchen (éds), Nonparametric and Semiparammetric Methods in Econometrics and Statistics: Proceedings of the Fifth International Symposium in Economic Theory and Econometrics, Cambridge University Press : Cambridge, 51-75.
- Pan, J. (2002), « The Jump-Risk Premia Implicit in Options: Evidence from an Integrated Time-Series Study », Journal of Financial Economics, 63 : 3-50.
- Silverman, B. W. (1986), Density Estimation for Statistics and Data Analysis, Chapman and Hall, 1986
- Yin, Y. Q. (1988), « Detection of the Number, Locations and Magnitudes of Jumps », Communications in Statistics–Stochastic Models, 4 : 445-455.
List of figures
Graphique 1
Rendements journaliers sur l’indice S&P 500 – 1980-2000
Graphique 2
Distribution de l’endroit des sauts estimés – DGP 2
Graphique 3
Distribution de la taille des sauts estimés – DGP 2
Graphique 4
Distribution de l’endroit des sauts estimés – DGP 4
Graphique 5
Distribution de la taille des sauts estimés – DGP 4
List of tables
Tableau 1
Valeurs des paramètres pour les expériences de simulation — valeurs estimées des rendements sur l’indice S&P 500 (2 janvier 1980–29 décembre 2000)
Tableau 2
Fréquence du nombre de sauts estimés pour DGP 1 (Le vrai nombre de sauts est zéro.)
Tableau 3
Fréquence du nombre de sauts estimés pour DGP 2 (Le vrai nombre de sauts est deux.)
Tableau 4
Fréquence du nombre de sauts estimés pour DGP 3 (Le vrai nombre de sauts est zéro.)
Tableau 5
Fréquence du nombre de sauts estimés pour DGP 4 (Le vrai nombre de sauts est deux.)
Tableau 6
Résultats de l’estimation de sauts dans la variance conditionnelle – rendements sur l’indice S&P 500, 2 janvier 1980–29 décembre 2000)